Коллоквиум Физика. Коллоквиум. 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде
 Скачать 3.24 Mb. Скачать 3.24 Mb.
|
Магнитное поле кругового тока (в центре витка).Напряженность м.п. в центре кругового тока: все эл-ты dH в этой точке перпендикулярны плоскости тока и направлены в сторону поступательного дв-ия правого винта, головка которого поворачивается по току. Величина напряженности М.п. кругового витка направлено по оси витка перпендикулярно к его плоскости. 32. Магнитное поле кругового тока (на перпендикуляре к центру витка). ;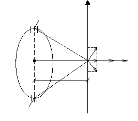 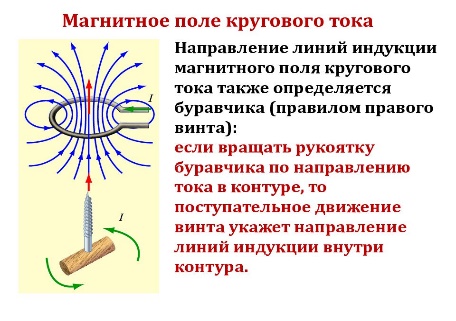 34. Поток вектора магнитной индукции. Теорема Гаусса для поля В Поток вектора магнитной индукцииПодробнее: https://zaochnik.com/spravochnik/fizika/magnitnoe-pole/potok-vektora-magnitnoj-induktsii/ Поток вектора магнитной индукции. Теорема Гаусса для поля вектора магнитной индукции. Поток вектора магнитной индукции, пронизывающий площадку S - это величина, равная: Поток вектора магнитной индукции (магнитный поток) измеряется в веберах (Вб) Магнитный поток - величина скалярная. Поток вектора магнитной индукции (магнитный поток) равен числу линий магнитной индукции, проходящих сквозь данную поверхность. Поток вектора магнитной индукции (магнитный поток) сквозь произвольную замкнутую поверхность равен нулю: Это теорема Остроградского-Гаусса для магнитного поля. Она свидетельствует о том, что в природе не существует магнитных зарядов – физических объектов, на которых бы начинались или заканчивались линии магнитной индукции. Как было показано выше, в природе нет магнитных зарядов. В 1931 г. П. Дирак высказал предположение о существовании обособленных магнитных зарядов, названных впоследствии монополи Дирака. Однако до сих пор они не найдены. Это приводит к тому, что линии вектора не имеют ни начала, ни конца. Мы знаем, что поток любого вектора через поверхность равен разности числа линий, начинающихся у поверхности, и числа линий, оканчивающихся внутри поверхности: . В соответствии с вышеизложенным, можно сделать заключение, что поток вектора через замкнутую поверхность должен быть равеннулю. Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие:
Это теорема Гаусса для(в интегральной форме): поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Этот результат является математическим выражением того, что в природе нет магнитных зарядов – источников магнитного поля, на которых начинались и заканчивались бы линии магнитной индукции. Заменив поверхностный интеграл в (1.7.1) объемным, получим:
где Это условие должно выполняться для любого произвольного объема V, а это, в свою очередь, возможно, если подынтегральная функция в каждой точке поля равна нулю. Таким образом,магнитное поле обладает тем свойством, что егодивергенциявсюду равна нулю:
В этом его отличие от электростатического поля, которое является потенциальным и может быть выражено скалярным потенциалом φ,магнитное поле – вихревое, или соленоидальное (см. рис. 1.3 и 1.8). 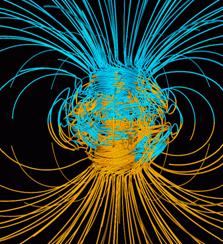 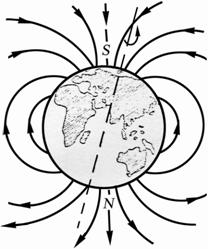 Рис. 1.9 Компьютерная модель магнитного поля Земли, подтверждающая вихревой характер, изображена на рис. 1.9. 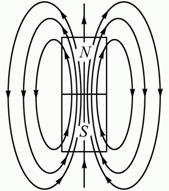 Рис 1.10 На рисунке 1.10 показаны магнитное поле постоянного магнита. Линии магнитной индукции замыкаются в окружающем пространстве. 35. 36. Работа по перемещению проводника с током в магнитном поле. |
