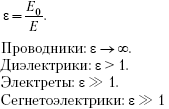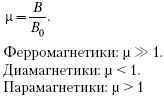Коллоквиум Физика. Коллоквиум. 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде

• Название: 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде
• Анкор: Коллоквиум Физика
• Дата: 01.12.2022
• Размер: 3.24 Mb.
• Имя файла: Коллоквиум.docx
• Тип: Закон; #822924
• страница: 3 из 14

Магнитное поле и его характеристики.

Магнитное поле - форма существования материи, окружающей движущиеся электрические заряды (проводники с током, постоянные магниты).

Магнитное поле имеет векторную силовую характеристику. Ее обозначают   и называют магнитной индукцией.

Магнитное поле изображается графически с помощью магнитных силовых линий или линий магнитной индукции. Магнитными силовымилинияминазываются линии, в каждой точке к которым вектор   направлен по касательной.

Линии магнитной индукции всегда замкнуты, что говорит об отсутствии в природе магнитных зарядов и вихревом характере магнитного поля.

Условно они выходят из северного полюса магнита и входят в южный. Густота линий выбирается так, чтобы число линий через единицу площади, перпендикулярную магнитному полю, было пропорционально величине магнитной индукции.

Н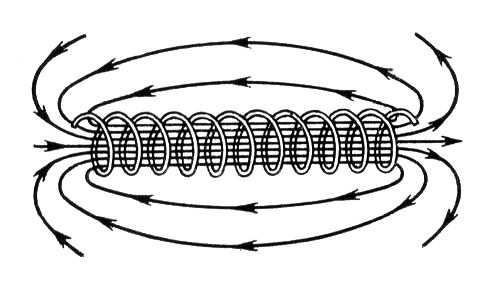

Магнитное соленоида с током

аправление линий определяется правилом правого винта. Соленоид - катушка с током, витки которой расположены вплотную друг к другу, а диаметр витка много меньше длины катушки.

Магнитное поле внутри соленоида является однородным. Магнитное поле называется однородным, если вектор   в любой точке постоянен.

Магнитное поле соленоида аналогично магнитному полю полосового магнита.

С  оленоид с током представляет собой электромагнит.

Для магнитного поля справедлив принцип суперпозиции: индукция магнитного поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме индукций магнитных полей, создаваемых каждым током или зарядом:



Вектор   вводится одним из 3-х способов:

а) из закона Ампера;

б) по действию магнитного поля на рамку с током;

в) из выражения для силы Лоренца.

С 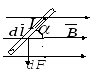ила   с которой магнитное поле действует на элемент проводника   с током I, находящегося в магнитном поле, прямо пропорциональна силе

тока I и векторному произведению элемента длины   на магнитную индукцию 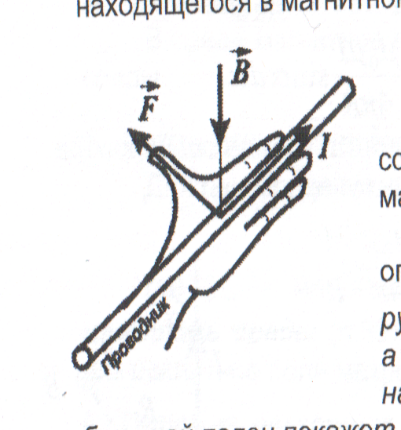 :  - закон Ампера

На правление вектора   может быть найдено согласно правилу левой руки: если ладонь левой руки расположить так, чтобы магнитные силовые линии входили в нее, а 4 вытянутых пальца направить по току, то отогнутый большой палец покажет направление силы.

Сила, действующая на провод конечной длины

При I = const, B=const, F = BIlsin

Если  =90⁰, F = BIl



Индукция магнитного поля - векторная физическая величина, численно равная силе, действующей в однородном магнитном поле на проводник единичной длины с единичной силой тока, расположенный перпендикулярно магнитным силовым линиям.

Магнитное поле макротоков описывается вектором магнитной напряженности  .

Для однородной изотропной среды

,

₀= 410^-7Гн/м - магнитная постоянная, ₀= 410^-7Н/А²,

 - магнитная проницаемость среды, показывающая, во сколько раз магнитное поле изменяется в данной среде.

Потоком вектора   (магнитным потоком) через площадку dS называется скалярная величина, равная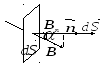



где   - проекция   на направление нормали к площадке;

 - угол между векторами   и  .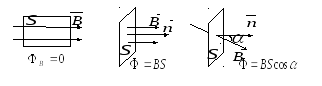

 - направленный элемент поверхности, 

 

Магнитный поток через поверхность S численно равен количеству магнитных силовых линий, пересекающих данную поверхность.

Поскольку линии магнитной индукции всегда замкнуты, для замкнутой поверхности число линий, входящих в поверхность (Ф<0) равно числу линий, выходящих из нее (Ф >0), следовательно, полный поток магнитной индукции через замкнутую поверхность равен нулю.

 - теорема Гаусса: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

Эта теорема является математическим выражением того, что в природе отсутствуют магнитные заряды, на которых начинались бы или заканчивались линии магнитной индукции.

Электрическое поле	Магнитное поле
Источники поля
Электрически заряженные тела	Движущиеся электрически заряженные тела (электрические токи)
Индикаторы поля
Мелкие листочки бумаги. Электрическая гильза. Электрический «султан»	Металлические опилки. Замкнутый контур с током. Магнитная стрелка
Опытные факты
Опыты Кулона по взаимодействию электрически заряженных тел	Опыты Ампера по взаимодействию проводников с током
Графическая характеристика
Линии напряжённости электрического поля в случае неподвижных зарядов имеют начало и конец (потенциальное поле); могут быть визуализированы (кристаллы хинина в масле)	Линии индукции магнитного поля всегда замкнуты (вихревое поле); могут быть визуализированы (металлические опилки)
Силовая характеристика
Вектор напряжённости электрического поля E. Величина:  Направление:	Вектор индукции магнитного поля В. Величина: .  Направление   определяется правилом левой руки
Энергетическая характеристика
Работа электрического поля неподвижных зарядов (кулоновcкой силы) равна нулю при обходе замкнутой траектории	Работа магнитного поля (силы Лоренца) всегда равна нулю
Действие поля на заряженную частицу
Сила всегда отлична от нуля: F = qE	Сила зависит от скорости движения частицы:  не действует, если частица покоится, а также если
Вещество и поле
.

28. Закон Био-Савара-Лапласа. Принцип суперпозиции полей.

Закон Био-Савара-Лапласа: каждый элемент   проводника с током   создает магнитное поле, вектор индукции которого 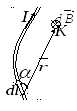  в некоторой произвольной точке К определяется по формуле: 

 - элемент проводника, сонаправленный с током;

 - радиус-вектор, соединяющий   c точкой K;

• 
  - угол между  и  .
  

А. Магнитное поле в центре кругового тока:



=90⁰, sin=1, 

Б. магнитное поле прямолинейного проводника с током.

Можно показать, что  ;

1. 
   для проводника конечной длины: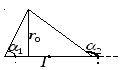
   

2. 
   для проводника бесконечной длины: ₁ = 0, ₂ = 
   

.

В. Поле внутри длинного соленоида с током.

B

Ø

=₀nI

где n - число витков на единице длины.

Принцип суперпозиции

Предположим наличие трех точечных зарядов, находящихся во взаимодействии друг с другом. При помощи эксперимента возможно осуществить измерение сил, действующих на каждый из зарядов. Для нахождения суммарной силы, с которой на один заряд действуют два других заряда, нужно силы воздействия каждого из этих двух сложить по правилу параллелограмма. При этом логичен вопрос: равны ли друг другу измеряемая сила, которая действует на каждый из зарядов, и совокупность сил со стороны двух иных зарядов, если силы рассчитаны по закону Кулона. Результаты исследований демонстрируют положительный ответ на этот вопрос: действительно, измеряемая сила равна сумме вычисляемых сил согласно закону Кулона со стороны других зарядов. Данное заключение записывается в виде совокупности утверждений и носит название принципа суперпозиции.

Определение 1

Принцип суперпозиции:

• 
  сила взаимодействия двух точечных зарядов не изменяется, если присутствуют другие заряды;
  
• 
  сила, действующая на точечный заряд со стороны двух других точечных зарядов, равна сумме сил, действующих на него со стороны каждого из точечных зарядов при отсутствии другого.
  

29. Закон Ампера. Взаимодействие параллельных токов.

Магнитное поле (см. § 109) оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент

испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током. Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнит­ном поле, равна

(111.1)

где dl—вектор, по модулю равный dl и совпадающий по направлению с током, В — вектор магнитной индукции.

Направление вектора dF может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца рас­положить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера (см. (111.1)) вычисляется по формуле

(111.2)

где  — угол между векторами dl и В.

Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I₁ и I₂; (направления токов указаны на рис. 167), расстояние между которыми равно R. Каждый из провод­ников создает магнитное поле, которое действует по закону Ампера на другой провод­ник с током. Рассмотрим, с какой силой действует магнитное поле тока I₁ на элемент dlвторого проводника с током I₂. Ток I₁ создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. На­правление вектора B₁ определяется правилом правого винта, его модуль по формуле (110.5) равен





Направление силы dF₁, с которой поле B₁ действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол  между элементами тока I₂ и вектором B₁ прямой, равен



подставляя значение для В₁, получим

(111.3)

Рассуждая аналогично, можно показать, что сапа dF₂ с которой магнитное поле тока I₂ действует на элемент dl первого проводника с током I₁, направлена в проти­воположную сторону и по модулю равна

(111.4)

Сравнение выражений (111.3) и (111.4) показывает, что

т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой

(111.5)

Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111.5).

30. Магнитное поле прямого тока.