Коллоквиум Физика. Коллоквиум. 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде

• Название: 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде
• Анкор: Коллоквиум Физика
• Дата: 01.12.2022
• Размер: 3.24 Mb.
• Имя файла: Коллоквиум.docx
• Тип: Закон; #822924
• страница: 5 из 14

На проводник с током в МП действуют силы, определяемые законом Ампера. Если проводник не закреплен (например, одна из сторон контура изготовлена в виде подвижной перемыч-

ки), то под действием FА он будет в МП перемещаться. Следовательно, МП совершает работу по перемещению проводника с током.

1. Для определения этой работы рассмотрим проводник длиной l с током I (он может свободно перемещаться), помещенный в однородное м.п. перпендикулярное к плоскости контура. Направление силы определяется по правилу левой руки, а значение – по закону АмпераF = IBl .

Под действием этой силы проводник переместится параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, совершаемая МП равна:

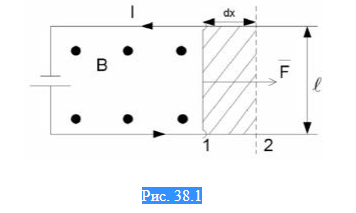
dA = FAdx = IBAdx = IBdS = IdФ

(38.1)

т.к.

41

Adx = dS – площадь, пересекаемая проводником при его перемещении в	(38.2)
магнитном поле.
Поток вектора магнитной индукции, пронизывающей эту площадь равен:
dΦ = BdS	(38.3)

Таким образом, работа по перемещению проводника с током в МП, равна произведению силы тока на магнитный поток, пересеченный движущимся проводником:

dA = IdФ

(38.4)

Полученная формула справедлива и для произвольного направления вектора B .

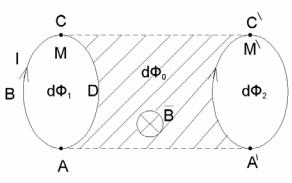
2. Вычислим работу по перемещению замкнутого контура с постоянным током в м.п. (произвольное движение). Предположим, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения займет положение M ′ . Направление тока в контуре

– по часовой стрелке и м.п. перпендикулярно плоскости чертежа.



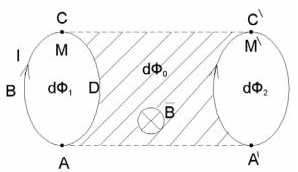
Рис 38.2

Контур М мысленно разобьем на два соединенных своими концами проводника: АВС и СDА. Работа dA, совершаемая силами Ампера при рассматриваемом перемещении контура в м.п., равна алгебраической сумме работ по перемещению проводников АВС и СDА (dA1 и dA2), то есть:

dA = dA1 + dA2

(38.5)

Силы приложенные к участку CDA контура образуют с направлением перемещения острые углы, поэтому совершаемая ими работа dA2>0. Эта работа, согласно формулам равна:

dA2 = I (dФ0 + dФ2 ) ,

(38.6)

где dФ0 – поток, который пересекает проводник CDA при движении; dФ2 – поток, пронизывающий контур в его конечном положении.

Силы, действующие на участок АВС контура, образуют с направлением перемещения тупые углы, следовательно dA1 <0. Проводник АВС пересекает при своем движении поток dФ0 сквозь поверхность и dФ1 – поток, пронизывающий контур в начальном положении.

Следовательно:

42

dA1 = −I (dФ0 + dФ1 ) .

(38.7)

Подставляя выражения для dA1 и dA2 в формулу (38.5), получим выражение для элементарной работы:

dA = −I (dФ0 + dФ1 ) + I (dФ0 + dФ2 ) ,	(38.8)
dA = I (dФ2 − dФ1 ) ,	(38.9)
где
dФ2 − dФ1 = dФ′	(38.10)
изменение магнитного потока сквозь площадь, ограниченную контуром с током.
Таким образом,
dA = IdФ′ .	(38.11)

Проинтегрировав это выражение, определим работу, совершаемую силами Ампера при конечном произвольном перемещении контура в м.п.:

A = I Ф.

(38.12)

Работа по перемещению замкнутого контура с током в МП равна произведению силы тока в контуре на приращение магнитного потока, сцепленного с контуром.

Формула (38.12) остаётся справедливой для контура любой формы в произвольном магнитном поле.