ответы на комплекты. 3М и 3П ответы. Вращательное движение
 Скачать 347.26 Kb. Скачать 347.26 Kb.
|
1 2 Физический смысл законаПотребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребитель, проходит и через источник тока, а значит, току кроме сопротивления проводника оказывается сопротивление самого источника. Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника. Физический смысл зависимости тока от ЭДС источника и сопротивления цепи заключается в том, что чем больше ЭДС, тем больше энергия носителей зарядов, а значит больше скорость их упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.  Зависимость можно показать на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения в цепи идет ток, наблюдаемый по амперметру, двигая ползунок реостата, увидим, что при изменении внешнего сопротивления ток будет меняться. Физический смысл электродвижущей силы, напряжения. ЭДС - электродвижущая сила. Измеряется в вольтах. В отличие от напряжения, это именно сила источника, которая зависит от внутреннего сопротивления источника. Целиком описывается законом Ома для полной цепи. То есть чем больше внутреннее сопротивление, тем слабее источник. Когда мы стягиваем через голову шерстяной свитер, мы слышим треск. В темноте видны и разряды в ткани. То есть напряжение достигает тысяч вольт, но огромное электрическое сопротивление шерсти делает ток ничтожным и безопасным для человека. Для электроники это значения не имеет. Переходы пробиваются именно напряжением, а потому для электроники статическое электричество особенно опасно. Физический смысл: Электрическое напряжение показывает, какую работу А совершает электрическое поле при перемещении единичного положительного заряда из одной точки в другую (при этом q= 1 Кл). Единица измерения напряжения называется вольтом В. За единицу напряжения принимают такое напряжение на концах проводника, при котором работа электрического поля по перемещению электрического заряда 1 Кл по этому проводнику равна 1 Дж. 1 В= 1 Дж/1 Кл Применяют другие единицы: милливольт, киловольт. 3. Напряженность электростатического поля. Определения, единицы измерения. Напряженность поля точечного заряда. Напряженность электрического поля. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля. E = F / q пр. Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд qпр, помещенный в рассматриваемую точку поля, к величине этого заряда. Понятие «пробный заряд» предполагает, что этот заряд не участвует в создании электрического поля и так мал, что не искажает его, т. е. не вызывает перераспределения в пространстве зарядов, создающих рассматриваемое поле. В системе СИ единицей напряженности служит 1 В / м, что эквивалентно 1 Н / Кл. Напряженность поля точечного заряда. Используя закон Кулона (1.1) найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда: 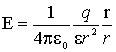 (1.2) (1.2)В этой формуле r – радиус-вектор, соединяющий заряды q и qпр. Из (1.2) следует, что напряжённость E поля точечного заряда q во всех точках поля направлена радиально от заряда при q > 0 и к заряду при q < 0. VI КОМПЛЕКТ Работа электрического тока. Мощность тока. При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном учестке совершает работу
где U = Δφ12 – напряжение. Эту работу называют работой электрического тока. Если обе части формулы
выражающей закон Ома для однородного участка цепи с сопротивлением R, умножить на IΔt, то получится соотношение
Это соотношение выражает закон сохранения энергии для однородного участка цепи. Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике.
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца. Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:
Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт). Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой
Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:
Первый член в левой части ΔQ = R I2Δt – тепло, выделяющееся на внешнем участке цепи за время Δt, второй член ΔQист = r I2Δt – тепло, выделяющееся внутри источника за то же время. Выражение Закон Ома в дифференциальной форме. Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)
Для однородного линейного проводника выразим R через ρ:
ρ – удельное объемное сопротивление; [ρ] = [Ом·м]. Найдем связь между В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока 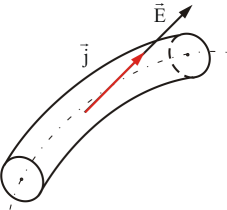 Рис. 7.6 Исходя из закона Ома (7.6.1), имеем: 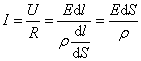 А мы знаем, что
это запись закона Ома в дифференциальной форме. Здесь Размерность σ – [ Плотность тока можно выразить через заряд электрона е, количество зарядов n и дрейфовую скорость Обозначим
Теперь, если удельную электропроводность σ выразить через е, n и b: 3. Зависимость удельного сопротивления от температуры. График зависимости. Практически в электротехнике выло выявлено, что с увеличением температуры сопротивление проводников из металла возрастает, а с понижением уменьшается. Для всех проводников из металла это изменение сопротивления почти одинаково и в среднем равно 0,4% на 1°С. Если быть точным, то на самом деле при изменении температуры проводника изменяется его удельное сопротивление, которое имеет следующую зависимость: 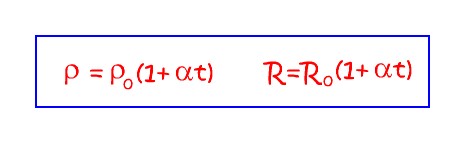 где ρ и ρ0, R и R0 - соответственно удельные сопротивления и сопротивления проводника при температурах t и 0°С (шкала Цельсия), α - температурный коэффициент сопротивления, [α] = град-1. Изменение удельного сопротивления проводника приводит к изменения самого сопротивления, что видно из следующего выражения:  Зная электронную теорию строения вещества можно дать следующее объяснение увеличению сопротивления металлических проводников с повышением температуры. При увеличении температуры проводник получает тепловую энергию, которая несомненно передается всем атомам вещества, в результате чего .возрастает их тепловое движение. Увеличившееся тепловое движение атомов создает большее сопротивление направленному движению свободных электронов (увеличивается вероятность столкновения свободных электронов с атомами), от этого и возрастает сопротивление проводника. С понижением температуры направленное движение электронов облегчается (уменьшается возможность столкновения свободных электронов с атомами), и сопротивление проводника уменьшается. Этим объясняется интересное явление — сверхпроводимость металлов. Сверхпроводимость, т. е. уменьшение сопротивления металлов до нуля, наступает при огромной отрицательной температуре —273° С, называемой абсолютным нулем. При температуре абсолютного нуля атомы металла как бы застывают на месте, совершенно не препятствуя движению электронов. График звисимости сопротивления металлического проводника от температуры представлен на рисунке 1. 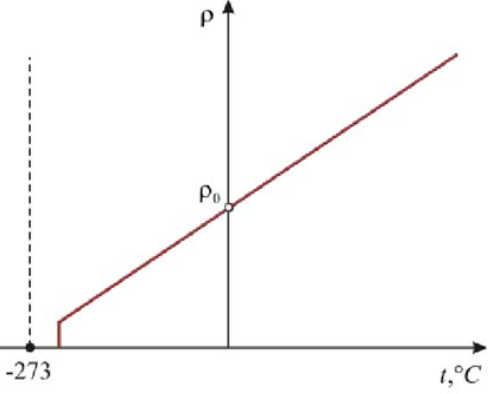 1 2 |
