Тема факторный анализ
 Скачать 50.5 Kb. Скачать 50.5 Kb.
|
|
Тема 3. ФАКТОРНЫЙ АНАЛИЗ Цель занятия: Ознакомить с основными способами систематизации факторов в детерминированном и стохастическом анализе, типами факторных детерминированных моделей и научить их применять в анализе финансово-хозяйственной деятельности предприятия используя MS Excel, обобщая и демонстрируя результаты анализа в наглядном графическом виде, выявлять возможные экономические и производственные резервы фирм на основе анализа формулировать аргументы и принимать управленческие решения. Ключевые слова: факторы, факторный анализ, детерменированный и стахостический анализ, правила моделирования. План лекции (1 час) 1. Необходимость и значение систематизации факторов. 2. Сущность и значение моделирования. Основные типы факторных детерминированных моделей. Стохастическое моделирование. Литература: осн.1,3,5,6,8,11,15, доп.1-6. 1. Необходимость и значение систематизации факторов В экономическом анализе под фактором понимается движущие силы, условия совершения хозяйственных процессов и причины, влияющие на них. Факторы взаимосвязаны между собой и нередко влияют на результаты деятельности в различных направлениях: одни положительно, другие – отрицательно. Все факторы классифицируются по различным признакам: 1) по степени воздействия на результаты работы делятся на: основные и второстепенные. К основным относят те, которые оказывают решающее воздействие на результаты работы. Их изучают в первую очередь, все остальные – второстепенные; 2) по степени количественного измерения влияния факторов на результат они подразделяются на: а) поддающиеся; б) неподдающиеся количественной оценке; 3) по времени воздействия факторы бывают: а) постоянные (влияющие непрерывно весь изучаемый период); б) временные (действующие определенный период); 4) факторы подразделяются на интенсивные и экстенсивные. Интенсивные связаны с наиболее эффективным применением достижений науки и техники, а экстенсивные – связаны с количественным расширением материально-технической базы предприятий и дополнительным привлечением трудовых ресурсов; 5) По охвату действием различают: а) общие факторы, которые присущи всем предприятиям не зависимо от сферы деятельности (состояние материально-технической базы, обеспеченность товарными ресурсами и эффективность их использования); 6) по характеру действия факторы бывают: а) объективные, не зависящие от результатов их функционирования; б) субъективные, зависящие от предприятий. 7) по действию на результаты деятельности предприятий факторы могут быть положительными и отрицательными. Факторы, влияющие на функционирования предприятий различных форм собственности тесно взаимосвязаны между собой. 2. Сущность и значение моделирования. Основные типы факторных детерминированных моделей. Стохастическое моделирование Все явления и процессы хозяйственной деятельности предприятий находятся во взаимосвязи и взаимообусловленности. Одни из них непосредственно связаны между собой, другие косвенно. Отсюда важным методологическим вопросом в экономическом анализе является изучение и измерение влияния факторов на величину исследуемых экономических показателей. Под экономическим факторным анализом понимается постепенный переход от исходной факторной системы к конечной факторной системе, раскрытие полного набора прямых, количественно измеримых факторов, оказывающих влияние на изменение результативного показателя. По характеру взаимосвязи между показателями различают методы детерминированного и стохастического факторного анализа. Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер. Основные свойства детерминированного подхода к анализу: - построение детерминированной модели путем логического анализа; - наличие полной (жесткой) связи между показателями; - невозможность разделения результатов влияния одновременно действующих факторов, которые не поддаются объединению в одной модели; - изучение взаимосвязей в краткосрочном периоде. Различают четыре типа детерминированных моделей: Аддитивные модели представляют собой алгебраическую сумму показателей и имеют вид 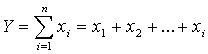 . .К таким моделям, например, относятся показатели себестоимости во взаимосвязи с элементами затрат на производство и со статьями затрат; показатель объема производства продукции в его взаимосвязи с объемом выпуска отдельных изделий или объема выпуска в отдельных подразделениях. Мультипликативные модели в обобщенном виде могут быть представлены формулой 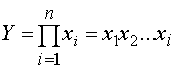 . .Примером мультипликативной модели является двухфакторная модель объема реализации где Ч - среднесписочная численность работников; CB - средняя выработка на одного работника. Кратные модели: 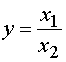 . .Примером кратной модели служит показатель срока оборачиваемости товаров (в днях) . ТОБ.Т: 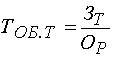 , ,где ЗТ - средний запас товаров; ОР - однодневный объем реализации. Смешанные моделипредставляют собой комбинацию перечисленных выше моделей и могут быть описаны с помощью специальных выражений: 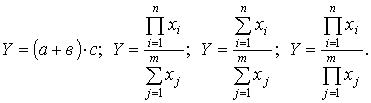 Примерами таких моделей служат показатели затрат на 1 тенге товарной продукции, показатели рентабельности и др. Для изучения зависимости между показателями и количественного измерения множества факторов, повлиявших на результативный показатель, приведем общие правила преобразования моделей с целью включения новых факторных показателей. Для детализации обобщающего факторного показателя на его составляющие, которые представляют интерес для аналитических расчетов, используют прием удлинения факторной системы. Если исходная факторная модель 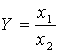 , а , а 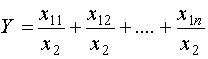 . .Для выделения некоторого числа новых факторов и построения необходимых для расчетов факторных показателей применяют прием расширения факторных моделей. При этом числитель и знаменатель умножаются на одно и тоже число: 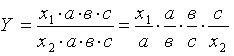 . .Для построения новых факторных показателей применяют прием сокращения факторных моделей. При использовании данного приема числитель и знаменатель делят на одно и то же число. 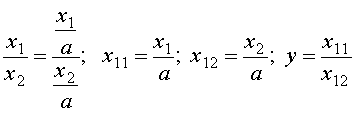 Детализация факторного анализа во многом определяется числом факторов, влияние которых можно количественные оценить, поэтому большое значение в анализе имеют многофакторные мультипликативные модели. В основе их построения лежат следующие принципы: - место каждого фактора в модели должно соответствовать его роли в формировании результативного показателя; - модель должна строиться из двухфакторной полной модели путем последовательного расчленения факторов, как правило, качественных на составляющие; - при написании формулы многофакторной модели факторы должны располагаться слева направо в порядке их замены. |
