Тема Конус Цели
 Скачать 116 Kb.
|
|
тема: Конус Цели: познакомить учащихся с понятием конуса, его элементами; вывести формулу, выражающую объем конуса и формулу площади боковой поверхности конуса; учить решать задачи; способствовать развитию логического мышления учащихся. Метапредметные результаты Регулятивные УУД: - планировать решение задачи; выбирать метод для решения, определять необходимые ресурсы; - планировать свою учебную познавательную деятельность; - осуществлять контроль в процессе своей деятельности; - осуществлять самоконтроль, коррекцию своих ошибок; - проводить самооценку результатов своей учебной деятельности. - находить, исправлять и объяснять ошибки. - анализировать причины успеха / неуспеха; - выделять достижения и трудности в работе; - организовывать себя на продуктивную работу; - принимать и удерживать учебную задачу; Познавательные УУД: - сопоставлять и обобщать содержащуюся в разных частях текста информацию; - систематизировать материал, полученный на предыдущих уроках; - систематизировать, обобщить затруднения при выполнении задания; - использовать знаково-символические средства для решения задач; - использовать знаково-символические средства представления информации; - преобразовывать информацию из одной формы в другую; - владеть рядом общих приемов решения задач (проблем); - выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий. Коммуникативные УУД: - строить рассуждение и доказательство своей точки зрения; - формулировать и аргументировано отстаивать свою точку зрения; - формулировать свои затруднения, возникшие при выполнении задания; - задавать вопросы с достаточной полнотой и точностью; - уважать позиции других людей, отличную от собственной; - учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве. Личностные результаты: - оценивать и осознавать свой вклад в общий результат урока; - связывать свои успехи с усилием, трудолюбием; ответственно относиться к учению; - вести диалог с другими людьми и достигать в нем взаимопонимания; - определять общие для всех правила поведения; Ход урока I. Проверка домашнего задания. 1. Один учащийся решает на доске задачу № 1214 (а) , заданную на дом. 2. С остальными учащимися проводится работа по ответам на вопросы 15–18 (с. 327 учебника). Решение задачи № 1214 (а). Дано: r = 2  см; h = 3 см. Найти: V.V = Sh = πr2h = π ∙ (2 )2 ∙ 3 = 24π (см3).Ответ:  см3.Решение задачи № 1244. Дано: d = 4 мм = 0,4 см; m = 6,8 кг; ρ = 2,6 г/см3. Найти: h (длину провода). ρ =  ; V = ; V = ≈ 2615 (см3); r = 0,2 см.Vцил = Sосн ∙ h = πr2h, отсюда h =  ≈ 20820 (см) ≈ 208 м.Ответ: ≈ 208 м. II. Изучение нового материала. Учитель демонстрирует модели конуса, лейку в виде конуса; можно свернуть из бумаги кулек в виде конуса. 1. Возьмем прямоугольный треугольник АВС и будем вращать его вокруг катета АВ (рис. 362, с. 328 учебника). В результате получится тело, которое называется конусом 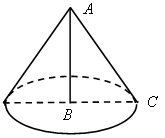 Учитель показывает на доске изображение конуса, учащиеся рисуют конус в тетради. 2. Прямая АВ называется осью конуса, а отрезок АВ – его высотой. При вращении катета ВС образуется круг, он называется основанием конуса. При вращении гипотенузы АС образуется поверхность, состоящая из отрезков с общим концом А (рис. 362). Ее называют конической поверхностью или боковой поверхностью конуса, а отрезки, из которых она составлена, – образующими конуса. Таким образом, конус – это тело, ограниченное кругом и конической поверхностью. 3. Пользуясь принципом Кавальери, можно доказать (см. задачу № 1219), что объем конуса равен одной трети произведения площади основания на высоту.  ,где r – радиус основания, h – его высота. 4. Ввести понятие развертки боковой поверхности конуса (рис. 363 а, б). Развертка боковой поверхности конуса представляет собой круговой сектор. Радиус этого сектора равен образующей конуса, то есть равен l, а длина дуги сектора равна длине окружности основания конуса, то есть равна 2πr. 5. Площадь Sбок боковой поверхности конуса равна площади ее развертки, то есть  ,где α – градусная мера дуги сектора (рис. 363, б). Длина дуги окружности с градусной мерой и радиусом l равна  . С другой стороны, длина дуги равна 2πr, то есть = 2πr, поэтомуSбок =  = 2πr ∙  = πrl.Итак, площадь боковой поверхности конуса с образующей l и радиусом основания r выражается формулой  .III. Выполнение упражнений. 1. Решить задачу № 1220 (б, в). Учащиеся решают самостоятельно, потом решение задачи проверяется. Решение б) Дано: r = 4 см; V = 48 π см3. Найти h. V =  πr2h; отсюда h = = 9 (см).Ответ: 9 см. в) Дано: h = m; V = р. Найти r. V = πr2h; найдем r2 = , тогда r = .Ответ:  .2. Решить задачу № 1221 на доске и в тетрадях. Решение Sосн = Q, Sбок = P. Найти V. 1) Sосн = πr2 = Q, отсюда r =  .2) Sбок = πrl = P, отсюда l =  . 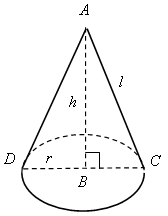3) По теореме Пифагора из Δ АВС найдем h2 = l2 – r2 =  .Значит, h =  .4) Найдем объем конуса V = πr2h = Q ∙  .Ответ:  .3. Решить задачу № 1222. Решение. По условию Sполн. конуса = 45π дм2; α = 60°. Найти V. V = πr2h.Sполн. конуса = Sосн + Sбок = πr2 +  ∙ α = πr2 + = πr2 + .Получили, что Sбок = , с другой стороны, Sбок = πrl, тогда приравняем эти два равенства, получим = πrl; разделим обе части на πl, получим  = r, отсюда l = 6r.По условию Sполн = 45π дм2, значит, 45π = πr2 +  ; 45π = πr2 + 6πr2; 45π = 7πr2,отсюда r2 =  .Из Δ АВС по теореме Пифагора найдем h2 = l2 – r2 = (6r)2 – r2 = 36r2 – r2 = 35r2 =  = 225.h =  = 15; h = 15 дм.Найдем объем конуса  (дм3).Ответ:  дм3.4. Решить задачу № 1248. Учитель объясняет решение задачи. Решение В тетрадях учащиеся записывают следующую теорему: «Объемы двух подобных тел относятся как кубы их соответствующих линейных размеров».
 = k3. Следовательно,  , отсюда V =  = 375 (см3).Ответ: 375 см3. 5. Решить задачу № 1249. Решение По условию h = 12 см, V = 324 π см3. Найти α дугу развертки боковой поверхности конуса. 1) V = πr2h;324π = πr2 ∙ 12;324 = 4r2; r2 = 81; r = 9 (см). 2) Sбок = ∙ α = πrl, отсюда, сократив обе части равенства на πl, получим  = r, тогда = 9, значит, α = .3) l2 = h2 + r2, то l =  = 15 (см).4) α =  = 216°.Ответ: α = 216°. 6. Решить задачу № 1250. Решение По условию α = 120°. Радиус развертки боковой поверхности конуса равен образующей конуса, то есть l = r1 = 9 см, где r1 – радиус сектора. 1) Sбок = ∙ α = ∙ 120° = 27π (см2).2) С другой стороны, Sбок = πrl, значит, 27π = π ∙ r ∙ 9, отсюда r = 3 см (это радиус конуса). 3) Sосн = πr2 = π ∙ 32 = 9π (см2). 4) h2 = l2 – r2, то h =  = ==  = 6 (см).Ответ: 9π см2; 6 см.IV. Итоги урока. Домашнее задание: изучить материал пункта 126; ответить на вопросы 19–22 (с. 336 учебника); решить задачу № 1220 (а); записать в тетрадь решение задачи № 1219 (с. 332 –333 учебника). |
OAB – общий угол;
Δ АО1D (по двум углам), тогда 
= k, значит, k =
.