ТЕМА 2. Логические формы мысли. Тема логические формы мысли План
 Скачать 56.2 Kb. Скачать 56.2 Kb.
|
        ТЕМА 2. Логические формы мысли ТЕМА 2. Логические формы мыслиПлан
2.1. Понятие……………………………………………………………..4 2.2. Суждение…………………………………………………………...6 2.3. Умозаключение…………………………………………………….8
Логика (древнегреч. logos - «слово», «мысль», «понятие») – это наука о фор мах, законах и операциях мышления. Объектом исследования логики является мышление. Логика, буду чи фило софской наукой, изучает формы выражения мыслей и формы развития знания, особые приемы и методы познания, а также особые законы и операции мышле ния. Предметом изучения логики являются формы мышления (отсюда название - «формальная логика»), а также законы и операции мышления. Различные по своему содержанию мысли могут иметь сходный внешний вид, они могут совпадать по своей ло гической форме, структуре. Логическая форма мысли – это строение данной мысли, ее структура, способ связи ее составных частей. Логическая форма не зависит от конкретного со держания, но служит для связи и упорядочения элементов этого содержания. Логическая форма на языке символической логики фиксируется с помощью разных видов переменных, а также логических констант. Именные переменные (S, Р – первые буквы латинских слов subjectumи predicatum) заменяют слова и словосочетания. Обозначив символом Sназвание предмета рассуждения, а символом Р название признака данного предмета в каждом из высказываний «Все бабочки – насекомые», «Все розы – цветы», по лучим следующую логическую форму этих утверждений: Все S суть Р. Пропозициональные переменные (строчные буквы конца латинско го алфа вита р, q, r, s, и др.) заменяют целые предложения, высказыва ния. Исходя из этого, логическую форму суждений «Если человек изучает логику, то он повы шает культуру своего мышления»; «Если предприятие получает прибыль, то оно рентабельно» можно предста вить следующей схемой: Если р, то q. «Уни версальные» переменные (прописные буквы начала латинско го алфавита А, В, С, D, и др.) заменяют как слова и словосочетания, так и целые предложения, высказывания. Логические константы (логические постоянные) – это выражения, сохра няющие свои значения в любых рассуждениях, независимо от контекста. В рас смотренных выше примерах в качестве логических констант использовались слова «все», «суть», «если, то». В роли логи ческих постоянных могут высту пать и другие выражения естественно го языка: «и», «или», «некоторые», «не верно, что», «ни... ни», «тогда и только тогда, когда» и др. Для обозначения ло гических констант в логи ке используют символы. Логический закон – это логическая форма, которая порожда ет истинные вы сказывания при любой подстановке вместо переменных их значений (конкрет ного содержания). Использование логических законов позволяет находиться в рамках истинного знания и на его основе продвигаться к новым знаниям, кото рые также будут ис тинными. 2. Основные формы абстрактного мышления Познание человеком окружающего его мира представляет довольно сложный процесс, в котором обычно выделяют две его разновидности: чувственное и ра циональное познание. Обе они тесным образом связаны между собой и каждая из них име ет свои формы. Познание человеком объективного мира начинается с по мощью органов чувств. Непосредственно взаимодействуя с те ми или иными предметами, мы получаем ощущения и восприя тия, которые становятся основой для представ лений. Результа ты полученных чувственных данных фиксируются и перераба тываются в нашем сознании с помощью рационального позна ния, которое нередко называют абстра ктным мышлением, в таких его основных формах как понятие, суждение и умо заключение. Абстрактное мышление, в отличие от чувственного позна ния, дает возможность проникнуть в сущность предмета, выя вить его отношения с другими предметами, уяснить закономер ности реального бытия. 2.1. Понятие Понятие представляет собой одну из форм познания, которая относится к мыслительной, интеллектуальной деятельности человека. Особая роль понятий в мыслительном процессе подтверждается тем, что, нередко, говоря о мыш лении, имеют в виду способность оперировать понятиями. Понятие, действительно, является основной единицей мыс лительной деятельности, так как без него невозможно выс казать ни одной мысли, невозможно провести никакого рас суждения. Понятие – это форма мышления, в которой отражаются существенные признаки одноэлементного класса или класса однородных предметов. В языке понятия выражаются посредством слов или словосочетаний (ягода, здание, добросовестный человек, полезное человеку растение). Выражая общие и отличительные, по преимуществу, суще ственные признаки, понятие не содержит всего богатства инди видуальных черт, которым обладает соответствующий ему пред мет, – и в этом оно проигрывает таким формам чувственного познания, как восприятие и представление. Вместе с тем, поня тие, несомненно, выигрывает в том, что оно позволяет сосредо точить внимание на главном, на существенном для данного предмета или их класса, что способствует более глубокому отоб ражению познаваемых предметов. Наиболее важными мыслительными операциями, исполь зующимися при формировании понятий, являются анализ (мысленное расчленение), син тез (мысленное объединение), сравнение (мысленное установление сходства или различия), обобщение (мысленное объединение однородных предметов в некото рый класс), а также абстрагирование и идеализация. При абстрагировании мы можем сосредоточить свое вни мание лишь на некоторых наиболее важных для данного мо мента признаках, оставив в стороне от рассмотрения все другие признаки предмета. Идеализация отличается тем, что в процессе этой мысли тельной операции мы или наделяем предметы свойствами, кото рых они на самом деле не имеют, или, наоборот, лишаем при сущих им в действительности каких-либо свойств (абсолютно черное тело, иде альная окружность, вечный двигатель и др.). В обыденном общении достаточно часто встреча ются слова, которые, будучи совершенно разными по своим значениям, пишутся и/или произносятся одинаково. Такие сло ва называют омонимами (докладывать, среда, топить и т.д.). Многозначные слова и различного рода омонимы могут быть препятствием для адекватного понимания речи, а могут использо ваться для усиления ее действенности. В языке обыденного общения есть и явление противополож ное омонимии. В этом случае имеют дело с разными словами или словосочетаниями, обозначающими один и тот же предмет (один и тот же класс предметов). Такие слова или языковые выражения называют синонимами (отечество, отчизна, родина). Наличие омонимов и синонимов необходимо учитывать как в устной, так и в письменной речи. При неправильном их употреб лении возможны логические ошибки. Предметы мира находятся друг с другом во взаимосвязи и взаимообус ловленности. Поэтому и понятия, отражающие эти предметы, также нахо дятся в определенных отношениях. Отношения между понятиями изображают с помощью круговых схем (кругов Эйлера), где каждый круг обозначает объем понятия. Кругом изобра жается и единичное понятие. Далекие друг от друга по своему содер жанию понятия, не имеющие общих признаков, называются несравнимыми (например, поэма и колодец; невоспитанность и радуга), осталь ные понятия называются сравнимыми. Деление сравнимых понятий дано в таблице: Сравнимые понятия Совместимые Несовместимые Равнозначные (тождественные) Перекрещивающиеся Подчиняющие и подчиненные Соподчиненные Противоположные Противоречащие А, В А В В А А В С D А В А В А – квадрат В – равносторонний прямоугольник А – студент В – рыболов А – рыба В – карп А – дуб В – береза С – осина D – дерево А – белые туфли В – черные туфли А – позвоночное животное В – беспозвоночное Каждое понятие можно охарактеризовать с двух сторон: со стороны содержания, и со стороны объема. Содержание – это совокупность признаков, с помощью ко торых проведено обобщение и выделение предметов, мыслимых в данном понятии. Объем понятия – это множество (класс) предметов, обоб щенных и выделенных в данном понятии. Между содержанием и объемом родственных понятий су ществует зависимость, называемая законом обратного отноше ния: чем больше объем понятия, тем меньше его содержание и, наоборот. Над понятиями могут осуществляться различные операции. Наиболее важными из них являются операции деления, обобщения и ограничения понятий. Деление понятия – это процедура перехода от данного понятия к совокупности подчиненных ему понятий с точки зрения некоторой характеристики, которая называется основанием деления. В ходе этой операции элементы объема исходного делимого понятия распределяются по подклассам, которые образуют объемы результирующих понятий – членов деления. Ограничение – логическая операция перехода от родового понятия к ви довому (например: поэт, великий поэт, великий русский поэт, великий русский поэт Михаил Юрьевич Лермонтов). При ограниче нии мы переходим от понятия с большим объемом к понятию с меньшим объемом. Пределом ограничения является единичное понятие (в данном примере это – великий русский поэт Михаил Юрьевич Лермонтов). Обобщение – логическая операция, обратная ограничению, когда осуще ствляется переход от видового понятия к родовому путем отбрасывания от первого его видообразующего признака или признаков. Понятия играют важную роль как в науке, так и в повседневной практике. Особое внимание обращается на точность используемой терминологии. Для достижения этой цели четко фиксируются смыслы употребляемых терминов, т.е. понятия о предметах, представляемых данными терминами. Адекватное понимание различных контекстов языка предполагает точное знание того, о каких типах объектов в них идет речь, т.е. знание понятий, связываемых с языковыми выражениями в этих контекстах. 2.2. Суждения Суждение – форма мышления, в которой что-либо утверждается или от рицается о существовании предметов, связях между предметом и его свойствами или об отношениях между предметами. Сужде ния выражаются в виде предложений, которые содер жат сообщение, какую-то информацию (Москва больше Минска; Ни один кашалот не является рыбой). Если то, о чем говорит ся в суждении, соответствует действительному положению вещей, то суж дение истинно. Указанные выше суждения являются истинными, так как в них верно отражено то, что имеет место в действительнос ти. В противном случае суждение ложно (Все растения являются съедоб ными). Суждения бывают простые и сложные. Последние состоят из нескольких простых. Суждение "Медведи делают запасы на зиму" – простое, а суждение "Наступила зима, выпал снег, и прилетели снегири" – сложное, состоящее из трех простых суждений. В простом суждении имеются субъект, предикат, а также могут быть связка и кванторное слово. В суждении "Некоторые птицы являются хищными" субъектом является понятие «птица», предикатом – понятие «хищник», кванторным словом – «некоторые», связка выражена словом «являются». Простые сужде ния бывают трех видов: 1.Суждения свойства (атрибутивные) – в них утверждается или отрицается принадлежность предмету известных свойств, состояний, видов деятельности (мед сладкий, три – нечетное число); 2. Суждения с отношениями – в них говорится об отношениях между предметами (семь меньше восьми, отцы старше своих детей). В суждении с отношением может что-либо утверждаться или отри цаться не только о двух, но и о трех, четырех или большем числе предметов (Москва находится между Санкт-Петербургом и Киевом); 3.Суждения существования (экзистенциальные) – в них утверждается или отрицается существование предметов (материаль ных или идеальных) в действительности (Сущест вуют атомные электростанции; Не существует беспричинных явлений). В традиционной логике все три указанных вида суждений представляют собой категорические суждения. Распределенность терминов в категорических суждениях можно выра зить схематически: знаком «+» выражена распределенность термина, а знаком «-» его нераспределенность. Без знания правил распределенности терминов в категорических сужде ниях отпадает один из способов проверки, правильно ли построен катего рический силлогизм или сделано непосредственное умозаключение. По качеству связки («есть» или «не есть») категорические суждения делятся на утвердительные (солнце светит) и отрицатель ные (луна не светит). В познании утвердительное суждение имеет в общем случае большее значение, чем отрицательное, ибо важнее раскрыть, каким признаком об ладает предмет, чем то, каким он не обладает, так как любой предмет не об ладает очень многими свойствами (например, дельфин не рыба, не насеко мое, не растение, не пресмыкающееся и т.д.). В зависимости от того, обо всем ли классе предметов, о части этого клас са или об одном предмете идет речь в субъекте, суждения делятся на общие (все Sсуть (не суть) Р), частные (некоторые S суть (не суть) Р) и единичные (это Sесть (не есть) Р). В каждом суждении имеется количественная и качественная характери стики. Поэтому в логике применяется объединенная классификация суж дений по количеству и качеству, на основе которой выделяются следующие четыре типа суждений: 1. А – общеутвердительное суждение (Все S(+) суть Р(±)). На пример: "Все люди хотят счастья". 2. I – частноутвердительное суждение (Некоторые S(-) есть Р(±)). Например: "Некоторые учащиеся увлекаются шахматами". 3. E – общеотрицательное суждение (Ни одно S(+)не есть Р(+)). Пример: "Ни один океан не является пресноводным". 4. O – частноотрицательное суждение (Некоторые S(-)не есть Р(+)). Например: "Некоторые люди не окончили школу". Сложные суждения образуются из простых суждений с помощью логи ческих связок: конъюнкции, дизъюнкции, импликации, эквиваленции и отрицания. Таблица истинности этих логических связок следующая:
Буквы a, b– переменные, обозначающие суждения; буква «И» обозна чает истину, а «Л» – ложь. Если в формулу входят п переменных, то таблица истинности для этой формулы, включающая все возможные комбинации истинности или лож ности ее переменных, будет состоять из 2n строк. Тождественно-истинной формулой назы вается формула, которая при любых комби нациях значений для входящих в нее пере менных принимает значение «истина». Тождественно-истинную формулу также называют законом логики. Тож дественно-ложная формула – та, которая (соответственно) принимает только значе ние «ложь». Выполнимая формула может принимать значения как «истина», так и «ложь». 2.3. Умозаключения Важнейшей способностью человека является способность размышлять, думать, мыслить. Мы сопоставляем какие-то факты, известные нам утверж дения, мысленно задаем вопросы и ищем на них ответы, пыта емся что-то кому-то доказать, объяснить, высказать предполо жения, сделать выводы. Во всех таких случаях мы имеем дело с рассуждением. Рассуждение – это мыслительный процесс, в ходе которого с помощью некоторых суждений, связанных между собой опреде ленным образом, получают другие суждения или обосновывают какие-либо высказывания. Рассуждения могут иметь различный характер. Одни из них имеют явным или неявным образом результат, с необходи мостью или некоторой степенью вероятности вытекающий из каких-либо суждений, – умо заключения. Другие представляют собой процесс обоснования истинности некоторого положения, – аргумен тация. Третьи имеют целью прояснить ту или иную ситуацию, объяснить причины некоторого явления или произошедшего события, раскрыть ме ханизм того или иного процесса, – объяснения. Четвертая группа рассуждений имеет отношение к перспективе или, наоборот, к ретрос пективе: к тому, что может произойти в будущем, или же к то му, что произошло в прошлом, – предс казания и постсказания. Из всех разновидностей рассуждений наибольший интерес для логики представляют умозаключения. Умозаключение – это мыслительный процесс, в ходе которо го из одного или нескольких суждений, называемых посылками, вы водится новое суждение. Умозаключения ши роко используются в теоретическом и обыденном познании, во всех видах профессиональной деятельности. Умозаключения лежат в основе всех других типов рассуждений, поэтому вполне понятно, что, научившись правильно строить умозаключения различного вида, можно с большей уверенностью пользоваться рассуждениями и других типов, успешно избегая тех или иных логических ошибок, подстерегающих человека, незнакомого с правилами различных умозаключений. При помощи умозаключений человек может получить те или иные знания о предмете, о котором он никогда раньше не имел ни малейшего представления. В общем виде структуру умозаключения можно предста вить следующим образом: 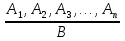 В этой схеме над чертой записывают посылки, а под чер той – заключение. Сама же черта заменяет слова «следователь но», «значит» и т.п. Если при этом истинность посылок гарантирует истинность заключения, то говорят, что в этом случае выполняется условие логического следования. Все умозаключения отличаются друг от друга способом построения, характеристикой посылок или заключения, иными свойствами. Прежде всего, в логике различают дедуктивные и недедуктивныеумозаключения. Дедуктивнымназывают умозаключение, в котором истин ность посылок должна гарантировать истинность заключения. Например: Все млекопитающие дышат легкими. Все киты – млекопитающие. Все киты дышат легкими. Здесь первая посылка "Все млекопитающие дышат легкими" является общеутвердительным суждением и выражает большую степень обобщения по сравнению с заключением, также являющимся общеутвердительным суждением "Все киты дышат легкими". Правила дедуктивного вывода определяются характером посылок, которые могут быть простыми (категорическими) или сложными суждениями. Различают правила: прямого вывода, которые позволяют из имеющихся истинных посылок полу чить истинное заключение; непрямого (косвенного) вывода – позво ляющие заключать о правомерности некоторых выводов из правомерности дру гих выводов. Прямые выводы различаются содержанием соответствующих типов суждений (посылок). Так бывают: чисто условные, чисто разделительные, условно-категорические, разделительно-категоричес кие и условно-разделительные (лемматические). К непрямым выводам относятся: рас суждение по случаям, сведе ние «к абсурду», рассуждение «от противного» (противоречащего). В дедуктивных умозаключениях, кроме вывода, учитывающего лишь способ связи между посылками, широко ис пользуются вывод, основанный на учете характера связи между терминами посылок. Такое умозаключение, в котором вывод строится на основе вза имосвязи между терминами одного или нескольких простых суждений называют силлогизмом. Примером такого умозаключения может быть такое рас суждение: "Все металлы – электропроводны. Медь есть металл. Медь – электропроводная". Силлогизмы делят на непосредственные, в которых заключение выводится из одной посылки, и опосредованные, в которых заключение выводится из двух посылок. Недедуктивныминазывают умозаключения, в котором ис тинность посылок не гарантирует истинности заключения. К ним относятся ин дуктивные умозаключения иумозаключения по аналогии. Индуктивное умозаключение – это умозаключение, в кото ром заключение о принадлежности некоторого признака каждо му элементу данного множества (класса) делается на основании изучения его отдельных элементов. В логике традиционно различают индукцию полную и неполную. Отличительной особенностью полной индукции является то, что ее заключение носит достоверныйхарактер. Вместе с тем, используя в своих рассуждениях полную индукцию, следует иметь в виду, что ее выводы будут правиль ными при выполнении определенных условий: 1. Если точно известно число предметов исследуемого класса. 2. Если число предметов исследуемого класса ограниче но и невелико. 3. Если установлено, что обобщаемый признак принад лежит действительно каждому предмету данного класса. 4. Если обобщаемый признак является существенным для изучаемого класса. Во многих случаях обыденной и научной практики умозак лючения полной индукции заменяются умозаключениями не полной индукции, которая при определенных условиях позво ляет получать заключения такой степени достоверности, кото рая удовлетворяет исследователя. Неполная индукция имеет две основных разновидностей: популярная и научная индукция. Популярная индукция или индукция через простое перечис ление – это вид неполной индукции, где заключение о принад лежности (не принадлежности) некоторого признака всем эле ментам данного множества делается на основании того, что этот признак обнаруживается (не обнаруживается) лишь у не которых произвольно взятых элементов этого множества при условии отсутствия противоречащих случаев. Примером такой индукции могут быть народные приметы связанные с погодой. Недостатки популярной индукции нивелируются при ис пользовании специальных научных методов, которые повыша ют степень вероятности индуктивных выводов, делают их более обоснованными и убедительными. Индукция, в которой ис пользуются такие методы, получила название научной. Необходимо иметь в виду, что на характере вывода отрицательно сказывается упущение следующих требований научной индукции: • планомерный и методический отбор предметов для исследования; • установление их существенных свойств, необходимых для самих предметов и важных для нашей практики; • раскрытие внутренней обусловленности этих свойств (признаков); • сопоставление полученного вывода с другими однотипными положениями науки в данной области знания. Выводы научной индукции не только дают обобщенные знания, но и раскрывают причинную связь, что представляет особую ценность процесса познания. Все умозаключения, относящиеся к научной индукции, можно разделить на две группы: индукцию через отбор и индук цию на основе причинно-следственных связей. Аналогия – заключение о сходстве в одних признаках на основании сходства в других. Формула аналогии: А обладает признаками а, в, с, е. В обладает признаками а, в, с. Вероятно, В обладает признаком е. Она имеет два вида: 1. Аналогия свойств, использующая в качестве признаков качества предмета (понятия); 2. Аналогия отношений, использующая отношение между предметами (понятиями). Нельзя смешивать в одном заключении два вида аналогии, вероятность выводов в этом случае не обеспечивается. Вероятность аналогии повышается также, если: - используются существенные признаки; - между признаками устанавливается сущностная взаимосвязь. Таким образом, соблюдение правил умозаключения по аналогии способствует повышению вероятности достижения истины в различных отраслях деятельности человека. 3. Упражнения. 1. Определите, какие формы мысли представлены в следующих языковых выражениях:
2. Приведите собственные примеры различных форм мысли и назовите их. Понятия: клавиатура, белый хлеб, пульт дистанционного управления, острый нож, подарочная открытка. Суждения: Кофе сегодня очень горячий; Компьютерные мыши бывают проводные и беспроводные; Моя тетрадь в клеточку и содержит двенадцать страниц; Вчера был дождливый день. Умозаключения: Так как гречневая крупа содержит мусор, ее необходимо перебрать; Если телевизор исправен, включен в розетку и настроен на необходимую частоту, то, вероятно, он покажет нужную нам программу; Для проезда в городском транспорте необходим билет. У меня есть нужный билет. Значит, я могу ехать на городском транспорте. 3. Определите, является ли выражение (рр) законом логики. Если да, то поясните каким? Составим таблицу истинности данного выражения:
Мы получили тождественно-истинную формулу, так как при любых комби нациях значений, для входящих в нее пере менных, формула принимает значение «истина». Следовательно, данное выражение является законом логики, законом противоречия. Где, два противоречащих друг другу высказы вания об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении, не могут быть одновременно истинными; по крайней мере, одно из них необходимо ложно. 4. Литература Бартон В.И. «Логика: учебное пособие для студентов высших учебных заведений». - Минск: Новое знание, 2005. Берков В.Ф., Яскевич Я.С., Павлюкевич В.И. «Логика: учебник для студентов высших учебных заведений». - Минск: ТетраСистемс, 2006. Галенок В.А. «Логика: учебное пособие». - Минск: Академия МВД Республики Беларусь, 2005. Гетманова А.Д. «Логика: учебник». - Москва: Омега-Л, 2006. Горбач Т.В., Лягушевич М.В. «Логика: учебно-методическое пособие». - Минск: БГМУ, 2006. Кузина Е.Б. «Логика: 100 вопросов - 100 ответов». - Москва: Владос, 2005. Малыхина Г. И. «Логика». - Минск, 2005. |

 b
b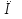 b
b b
b b
b