ХА ХА ХА ЗАСКАМИЛА МАМОНТА. Основы МатКад. Тема математические величины и простые выражения
 Скачать 441.17 Kb. Скачать 441.17 Kb.
|
|
Тема 1. МАТЕМАТИЧЕСКИЕ ВЕЛИЧИНЫ И ПРОСТЫЕ ВЫРАЖЕНИЯ В простейшем случае работа с системой MathCAD сводится к подготовке в окне редактирования задания на вычисления и к установке форматов для их результатов. Набор упрощается, если использовать клавиатуру и математические палитры. Для запуска формульного редактора достаточно установить курсор мыши в любом свободном месте окна редактирования и щелкнуть левой клавишей. Появится визир в виде маленького красного крестика. Его можно перемещать клавишами перемещения курсора. Визир не надо путать с курсором мыши, который имеет вид жирной наклонной стрелки. Прежде чем приступить к конкретным расчетам, необходимо отметить, что в MathCAD существует два знака равенства =, : =, которые существенно различаются. Знак = имеет смысл либо логического равенства, либо оператора «выполнения» расчета. Знак : = – это оператор присвоения значения. Простейшими элементами MathCAD являются числовые константы. Например, 68, 52.137, 7.9·10-26. Система MathCAD может также работать с восьмеричными и шестнадцатеричными числами. Разделителем целой и дробной части является точка. Большинство вычислений система выполняет как с действительными, так и с комплексными числами, которые обычно представляются в алгебраическом виде: Z = X + 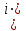 Y, Y, где X = Re Z – действительная часть числа Z, Y = Im Z – мнимая часть числа Z; i – мнимая единица. Комплексное число может быть задано в экспоненциальной форме: Z = R· е-iφ, R = 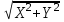 , tg φ = Y/X, , tg φ = Y/X, где R – модуль комплексного числа; φ – его аргумент. Например, Z = 3 + i·5, Z = i·7.4, Z = 8.54·еi·7. В системе может применяться особый вид констант – размерные величины. Помимо своего числового значения они характеризуются еще и указанием размерности физической величине. Для этого указания используется символ умножения. В системе MathCAD заданы следующие основные типы физических величин: time (время), length (длина), mass (масса), charge (заряд) и др. Например, 6.7 kg (килограмм), 1 А (Ампер), 2.63 s (секунд) и т.д. Самостоятельно рассчитать следующие математические выражения: 1) 3.2·7.28 – (6+9.1·4.6):(1.2-7.43); 2) (31.6- 6.2·3)2 - 3.7:1.3·0.86 + 7.31; 3) 4.5·103 ·(3 –(1.6- 8.4·1.7)):7.8; 4) (3.4 +i·5.7)·(6 – i·2); 5) 6.4·kg·8.34·m2; 6) 8.6·A·1.86·m:(4.6·s). 1.1. Определение переменных Переменные являются поименованными объектами, имеющими некоторое значение, которое может изменяться по ходу выполнения программы. Имена констант, переменных и иных объектов называют идентификаторами. Тип переменной определяется ее значением; переменные могут быть числовыми, строковыми, символьными и т.д. Идентификаторы в системе MathCAD могут иметь практически любую длину, и в них могут входить любые латинские и греческие буквы, а также цифры. Однако начинаться идентификатор может только с буквы, например: X, Y1, mass. В MathCAD существует особый класс системных переменных. Это число π, основание натурального логарифма е, TOL – погрешность численных методов (по умолчанию -0.001), ORIGIN – нижняя граница индекса массива (по умолчанию 0). Все переменные в MathCAD, кроме системных, должны быть определены пользователем. Существуют два оператора присваивания: оператор локального присваивания: = и оператор глобального присваивания ≡. Глобальное присвоение значения переменной может производиться в любой части документа и будет действовать везде. Попытка использовать неопределенную переменную ведет к выводу сообщения об ошибке – переменная окрашивается в ярко-красный цвет. Примеры определения простой переменной: X : = 12.83, Z3 : = 6.25·10-5, alfa : = 3 + i· 5.6, y : = 3 kg. Самостоятельно задайте значения необходимых параметров и вычислите следующие математические выражения, при этом следует помнить, что значения переменных должны располагаться выше выражений: 1) 2) 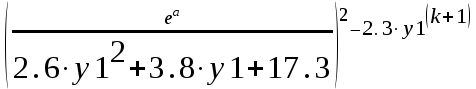 . . 1.2. Ранжированная переменная (дискретный аргумент) Ранжированные переменные – это набор фиксированных значений величин, меняющихся от начального значения до конечного с определенным шагом. Ранжированные переменные характеризуются именем и индексом каждого своего элемента. Например, если переменная величина x изменяется от 0 до 10 с шагом 1, то такая переменная задается в виде x := 0..10. Для ввода символа используется кнопка m..n палитры Matrix (матрица). Использовать клавиатурные точки нельзя. Для определения диапазона значений переменной t от 10 до 20 с шагом 0.1 используется конструкция t : = 10, 10.1.. 20, включающая начальное значение интервала, начальное плюс шаг и конечное значение интервала. Вывести значения переменной или математического выражения на экран можно с помощью знака «выполнить» =. Например, записи x =, sin(x)= вызывают появление на экране численных значений величин либо таблицы величин, если они заданы в ранжированном виде. Примеры показаны на рис.1.1. 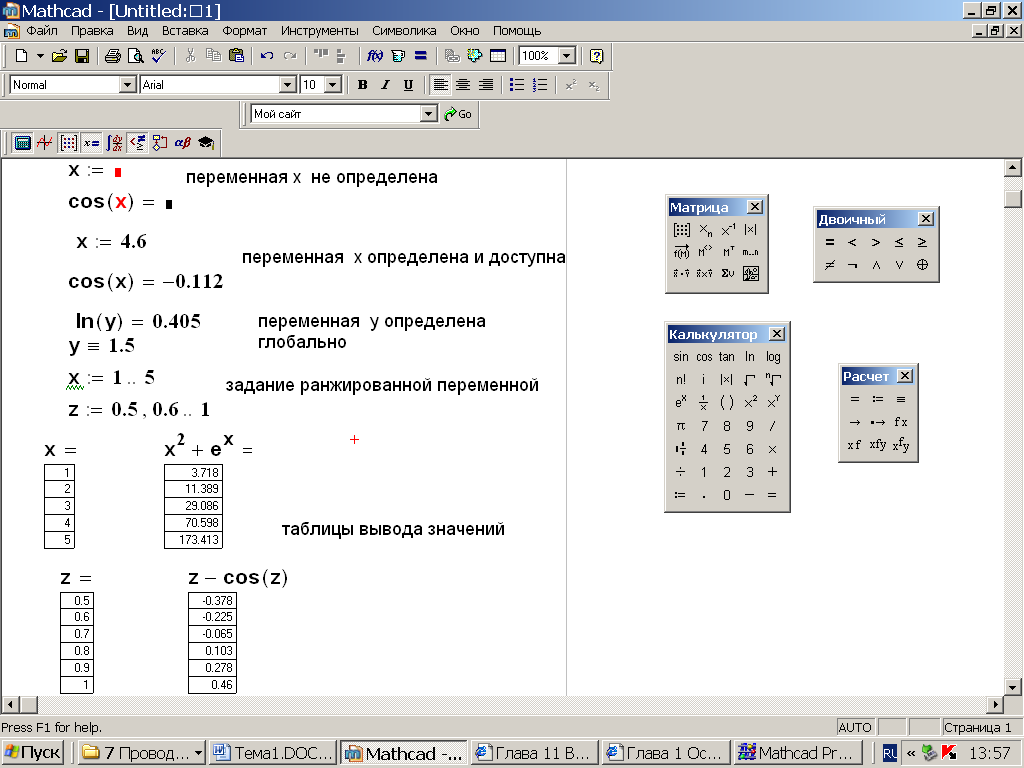 Рис. 1.1 Самостоятельно вычислите значения следующих выражений с шагом 0.1, 0.25, 1 для 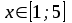 , учитывая, что некоторые тригонометрические функции в MathCAD пишутся иначе: tan, asin вместо tg, arcsin: , учитывая, что некоторые тригонометрические функции в MathCAD пишутся иначе: tan, asin вместо tg, arcsin:1) 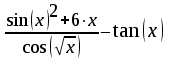 ; ;2) 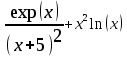 . .УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ПО ПЕРВОЙ ТЕМЕ Арифметические выражения, переменные, функции 1. Вычислить: 1) 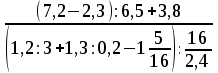 ; ;2) 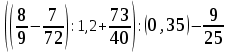 ; ;3) 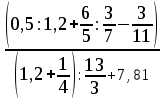 ; ; 4) 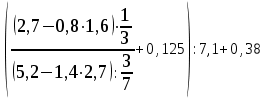 ; ;5) 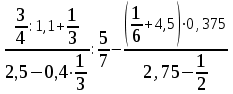 ; ;6) 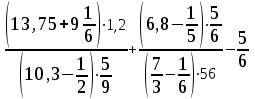 ; ;2. Вычислить: 1) 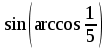 ; 2) ; 2) 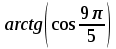 ; ;3) 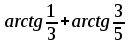 ; 4) ; 4) 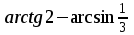 . .3. Вычислить значения выражений: 1) 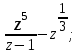 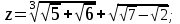 2) 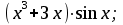 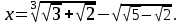 4. Задать ранжированную переменную: 1) переменная х меняется в пределах от 0 до 7 с шагом 1; 2) переменная х меняется в пределах от – 5 до 5 с шагом 1; 3) переменная х меняется в пределах от 1 до 2 с шагом 0,1; Тема 2. ФУНКЦИИ И МАТЕМАТИЧЕСКИЕ ОПЕРАТОРЫ 2.1. Определение функции Функции так же, как и переменные, задаются с использованием оператора присвоения :=. Идентификатор функции может включать в себя латинские буквы, цифры и другие символы. В скобках обязательно указываются аргументы функции. Набор основных стандартных функций лучше производить из наборной палитры «Arithmetic (Калькулятор)» или выбрав опцию f(x) на панели инструментов. В последнем случае представлены практически все функции, используемые в математике и физике. При нажатии на кнопку, соответствующую вводимой функции, на экране появляется шаблон функции sin (■), в который проставляется аргумент или другие параметры в более сложных функциях. Пользователь может сам задать функцию необходимую для расчета. Определим, например, с помощью кинематического уравнения движения точки падающей в поле силы тяжести, высоту: 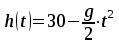 , g =9.8. , g =9.8.1. Определим значение функции в точке t = 2. 2. Определим значения функции для каждого значения ранжированной переменной t из диапазона значений: t:= 1÷2 с шагом 0.1. Решение. Задаем значения ранжированной переменной t, затем функцию h(t) и выполняем расчет:   Самостоятельно вычислите значение функции f(z) = sin(z)3+ cos(z)3 в точках 0, 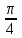 , , 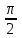 , , 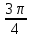 , π, , π, 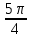 , , 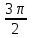 , ,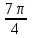 , 2π. , 2π.2.2. Математические операторы Операторы представляют собой элементы языка, с помощью которых можно создавать математические выражения. К ним, например, относятся символы арифметических операций, знаки вычисления сумм, произведений, производной и интеграла и т.д. После указания операндов (параметров операторов) операторы становятся исполняемыми по программе блоками. Для ввода математических операторов используется математическая палитра «Calculus (Вычисления)» (нажмите соответствующую кнопку на палитре). Выберите нужный оператор щелчком мыши и в появившемся шаблоне оператора заполните пустые поля необходимыми параметрами. Переход между полями внутри математического выражения осуществляется клавишами перемещения курсора или «пробелом». На рис. 2.1 представлены процедуры ввода математических операторов и примеры расчетов производных, интегралов и сумм. 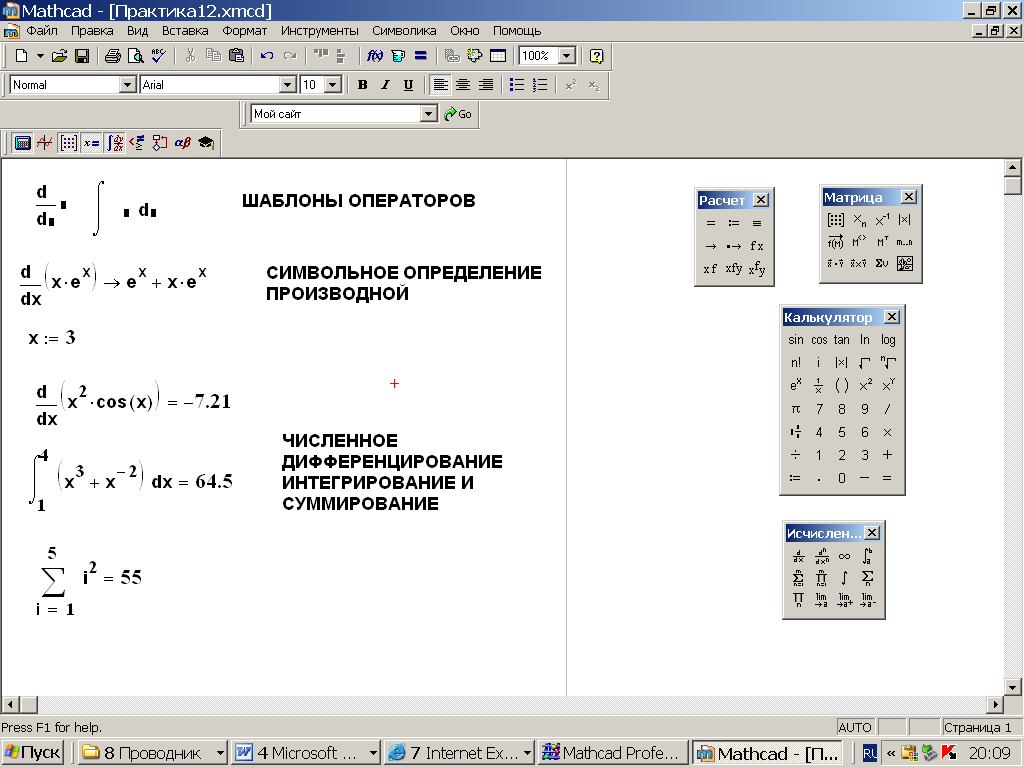 Рис. 2.1 MathCAD позволяет производить как численное дифференцирование и интегрирование, если заданы значения аргумента функции, так и аналитическое решение в общем виде. Для этого в программе существует символьный процессор. Символьной математике будет посвящена специальная тема, в этом же разделе заметим лишь, что аналитическое выражение для производной или интеграла можно получить с помощью палитры «Evaluation (Расчет)» кнопка →, как показано на рис.2.1. Рассмотрим конкретные примеры определения производных, интегралов, сумм и других математических операций. 1. Определим вторую производную функции f(x) = x·ex + x2· sin x, если х меняется в пределах от 1 до 5. Для этого введем новую функцию g(x) вида:  g(x) = 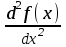 , зададим ранжированную переменную х := 1..5 и выведем значение функции g(x) в виде таблицы: , зададим ранжированную переменную х := 1..5 и выведем значение функции g(x) в виде таблицы:  2. Рассчитаем определенный интеграл от той же функции f(x) = x·ex + x2· sin x с переменным верхним пределом интегрирования. Обозначим этот интеграл:   параметр а меняется в пределах а := 1..4, тогда значения интегралов получим в виде таблицы: 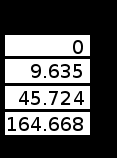 3. Найдем массу треугольника, задаваемого неравенствами 0 Поверхностную плотность треугольника можно определить соотношением 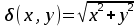 , тогда масса будет равна , тогда масса будет равна 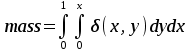 . Расчет массы дает mass =0.373. . Расчет массы дает mass =0.373.4. Рассчитаем пределы функций 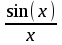  ; ;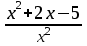 при х→ 0. Для этого выводим шаблоны пределов и вставляем в них функции и нажимаем кнопку «Символьный расчет» (→) в палитре «Evaluation (Расчет)». В результате на экране появляется результат: при х→ 0. Для этого выводим шаблоны пределов и вставляем в них функции и нажимаем кнопку «Символьный расчет» (→) в палитре «Evaluation (Расчет)». В результате на экране появляется результат: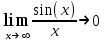 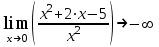 УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ПО ВТОРОЙ ТЕМЕ 1. Задать функцию и определить ее значения в указанной области: 1) y(x) = 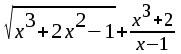 , х = 1..10; , х = 1..10;2) Ф(φ) = tg (sin2 φ) - 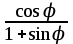 , , 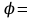 0, π/4..π; 0, π/4..π;3) у(х) = 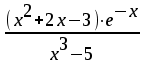 , х = 5, 5.1..6. , х = 5, 5.1..6.Вычислите символьно и (или) численно (значения переменной задайте самостоятельно): 1) 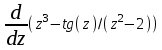 ; 2) ; 2) 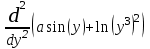 ; ;3) 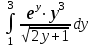 Тема 3. ВЕКТОРЫ И МАТРИЦЫ Важным типом данных в системе MathCAD являются массивы. Массив – имеющая имя совокупность конечного числа числовых или символьных элементов, упорядоченных заданным образом и имеющих определенные адреса. В системе MathCAD используются массивы двух наиболее распространенных типов: одномерные (векторы) и двумерные (матрицы). Для задания имени (идентификатора) массива обычно используются латинские буквы и цифры M, N1, vec… Порядковый номер элемента массива, который является его адресом, называется индексом. Нижняя граница индексации задается значением системной переменной ORIGIN, которой можно присвоить значения 0 или 1(по умолчанию 0). Индексы принимают только целочисленные значения и часто задаются ранжированной переменной i := 0..3, j := 1..5. Элементы массива обозначаются идентификаторами с подстрочными индексами Mi,j, N0,1. Подстрочные индексы вводятся нажатием клавиши открывающейся квадратной скобки [ или кнопкой хn палитры «Матрица». П  рисваивание значений индексированным элементам массивов происходит так же, как и обычным переменным с помощью оператора присваивания : = рисваивание значений индексированным элементам массивов происходит так же, как и обычным переменным с помощью оператора присваивания : = Чтобы вектор U был представлен в виде строки, необходимо его элементы задать в виде матрицы вида U0,i. Ввести значения элементов массива можно с помощью шаблона вектора или матрицы, который находится в палитре «Vector and matrix» (Матрица). После нажатия на соответствующую кнопку на экране появляется диалоговое окно, в котором нужно указать размерность вектора или матрицы и затем выводится шаблон (рис.3.1). После заполнения всех элементов шаблона массив может быть использован для расчетов. Зададим с помощью шаблона две трехмерные матрицы N, M и два вектора v, f. Рассмотрим основные операции с векторами и матрицами.     Если массивы заданы шаблонами, то можно вывести любой элемент массива, например, второй элемент вектора v будет равен v1 = 4 или элемент матрицы M1,2 = 5. Результаты основных арифметических операций с векторами и матрицами будут следующими:   где vT – транспонированный вектор; M-1 – обратная матрица, знак (·) означает скалярное произведение векторов, а знак (х) – векторное произведение векторов. На рис.3.1 также показаны некоторые операции с массивами. 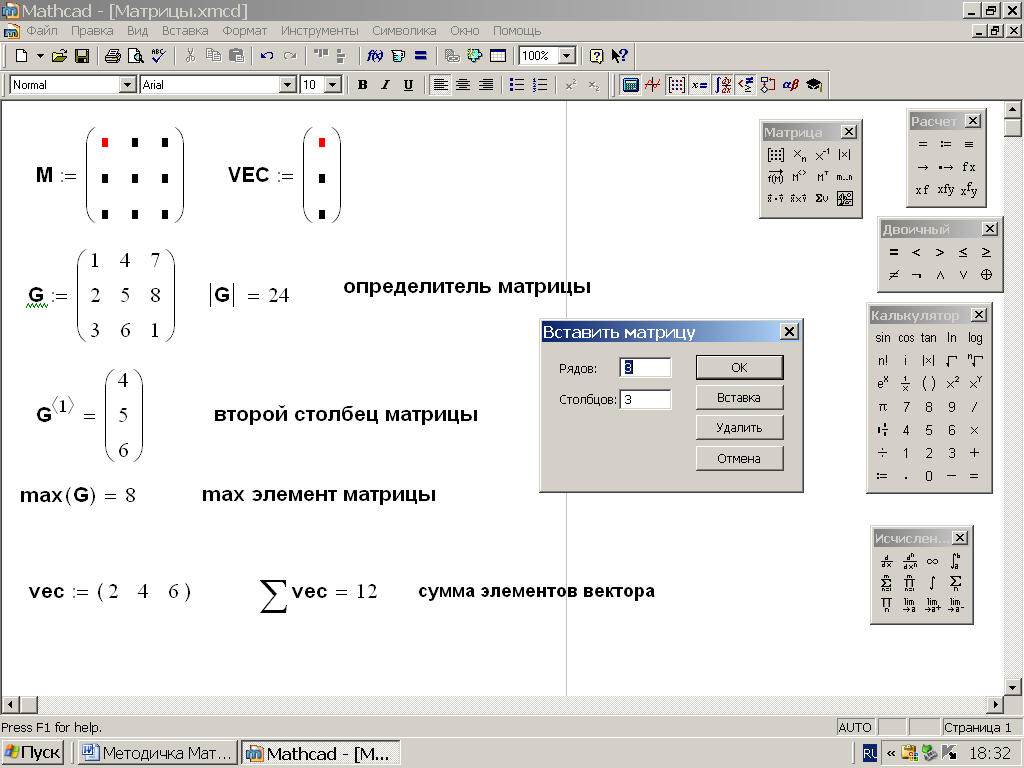 Можно производить операции с матрицами, заданными различными способами, например,  Часто в теории матриц используется единичная матрица Е. Эту матрицу можно задать несколькими способами. Первый способ – с помощью условного оператора if:  Кроме того, в MathCAD существует функция, возвращающая единичную матрицу identity(■), в скобках указывается размерность матрицы:  При решении практических задач возникает проблема одновременного подсчета значения функции в большом числе точек. Эту проблему можно решить, представив значения аргумента функции в виде матрицы, и затем взять функцию от матрицы. Для этого в MathCAD существует операция векторизации, которая в палитре «Vector and matrix» (Матрица) представлена значком  Например, если задана матрица М, то функции sin(M), Например, если задана матрица М, то функции sin(M), 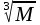 будут равны будут равны  Рассмотрим задачу о векторизации матрицы, заданной функцией exp(K2+1) +K, где матрица K размерности 3х3 задана в виде Ki,j = i + j. Решение этой задачи представляется в виде:  Матричными методами можно решать линейные системы уравнений. Рассмотрим систему уравнений вида: x + 3 y + 4 z = 0; 3 x + 4 y + 5 z =1; 4 x + 5 y + 6 z =2. В матричном виде это уравнение можно записать A* X =B, где А – матрица коэффициентов при неизвестных величинах; X – вектор неизвестных величин; B – правые части уравнений. Решение системы будет X = B* A-1. В MathCAD решение этой задачи представляется в виде:  УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ПО ТРЕТЬЕЙ ТЕМЕ 1. Выполнить действия над матрицами 2(A+B)(2B-A), где 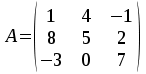 ; ; 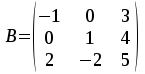 . .2. Решить уравнение 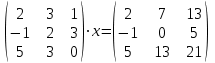 . .3. Выполнить действия над матрицами (А2-В2)*(2*А+В), где 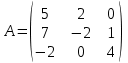 ; ; 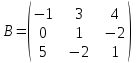 . .Тема 4. ПОСТРОЕНИЕ ГРАФИКОВ В системе MathCAD для вывода и интерпретации результатов расчета используется двухмерная (2D) и трехмерная (3D) графика. Двухмерная графика подразумевает графическое представление в декартовой (График Х-У) и полярной (Полярный график) системе координат. 3D графика используется для построения трехмерных поверхностей (Surface Plot), контурных графиков (Contour Plot), 3D гистограмм (3D Bar Chart) и других трехмерных объектов. Соответствующие пиктограммы изображены в палитре «Graph (Графики)». 4.1. Двухмерная графика Для построения двухмерного графика необходимо нажать на соответствующую пиктограмму (кнопку) палитры «Graph (Графики)», в результате чего на экране появляется шаблон графика рис.4.1. Далее, если по вертикали указать функцию f(x), график которой требуется построить, а по горизонтали – независимую переменную x, то на экране отобразится график функции f(x). При этом по умолчанию аргумент изменяется от -10 до +10, если нет ограничений. На одном и том же графике можно построить несколько функций, указав их через запятую в вертикальной позиции шаблона (см. рис.4.1), при этом все графики будут иметь разный цвет. Вообще формат представления любой информации в MathCAD, в том числе и графиков, можно менять. Для этого необходимо выставить курсор на соответствующий объект и щелкнуть правой клавишей мыши во всплывающем меню выбрать позицию формат, и далее менять параметры осей или трассировку (графических линий). Описанный выше способ построения графиков может быть использован лишь для простых функций. В общем случае необходимо предварительно задать область изменения аргумента функции и саму функцию, а затем строить ее график. На рис.4.1 показан алгоритм построения графика функции F(x) = sin(x)/x.  Рис. 4.1 Для изменения размеров рисунка нужно точно подвести графический курсор к специальным шаблонам на рамке, выделяющей рисунок. Эти шаблоны имеют вид маленьких черных прямоугольников. Изображение курсора при этом меняется на двустороннюю стрелку, указывающую, в каких направлениях можно растягивать рисунок. Нажав левую клавишу мыши, можно захватить соответствующую сторону или угол шаблона рисунка и, не отпуская клавишу, начать растягивать или сжимать шаблон. После того как клавиша будет отпущена, рисунок перестроится в новых размерах. Сжимать и растягивать графики можно в вертикальном, горизонтальном и диагональном направлениях. Особо следует отметить возможность помещения текстовых комментариев в область графиков. Для этого вначале надо подготовить их в стороне от графика и выделить пунктирной линией. Затем, поместив курсор мыши в область текста, надо нажать ее левую клавишу и перенести текстовый блок в область рисунка. Установив текст в нужном месте, отпустите клавишу мыши рис.4.3. Рассмотрим некоторые примеры построения графиков в декартовой системе. Построим график фигуры, заданной в параметрическом виде xi = sin ( 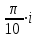 ), yi = cos ( ), yi = cos (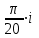 ), i – дискретный параметр, меняющийся в пределах от 0 до 50. Решение этой задачи в MathCAD представляется в виде (рис.4.2): ), i – дискретный параметр, меняющийся в пределах от 0 до 50. Решение этой задачи в MathCAD представляется в виде (рис.4.2):    Рис. 4.2 2. Рассмотрим графическое представление многомерного вектора, заданного компонентами yj = 0.35j · 0.6510-j, где j меняется в пределах 1 ÷ 10. Компоненты вектора на графике представим точками и сплошными столбцами. Зададим в виде ранжированной переменной параметр j: j := 1..10 и введем с подстрочным индексом вектор yj. В шаблон декартового графика вставим параметры j и yj. В результате получим: компоненты вектора 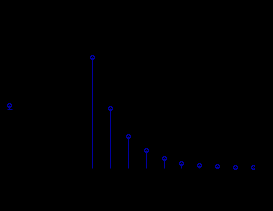 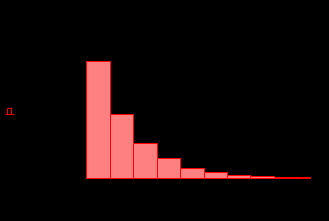 Рис. 4.3 Различная форма представления графиков может быть задана при форматировании. Общие принципы форматирования графиков рассматривались выше. В данном случае необходимо выбрать опцию «Traces (Трассировка)», где можно менять тип (Type), цвет (Color), толщину (Weight) линии, а также отображать график различными символами (Symbol). В нашем примере (см. рис.4.3) были выбраны два типа линий «Points (точки)» и «Solid bar (Сплошной столбец)». Построение графиков в полярной системе координат по своим принципам мало отличается от декартовых графиков. Также необходимо задать отображаемую функцию и область изменения аргумента функции. Аргументом чаще всего является угловой параметр. Рассмотрим примеры построения полярных графиков: 1. Построить график зависимости R(α)= sin (α/2) + cos (α/2) при изменении α в пределах 0 ÷ 2π. Вводим значения параметра α и функцию R(α). Выводим шаблон полярного графика из палитры «Graph (Графики)» и проставляем аргумент α по горизонтали, а функцию R(α) по вертикали шаблона. В результате получим:   Полярный график 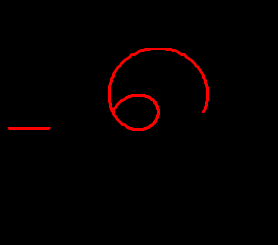 Рис. 4.4 На рис.4.4 представлены два формата отображения полярного графика. В первом случае тип трассировки «Lines (Линия)», во втором – «Bar (Столбец)» и, кроме того, стиль оси в первом случае «Периметр», а во втором – «Пересечение». На первом графике также показана возможность создания текстовой надписи в нижней или верхней части графика. Для этого существует опция «Labels (Метки)» в меню форматирования. Необходимо ввести текст надписи и указать положение надписи: в верхней или нижней части графика. Следует отметить, что графики, построенные в полярной системе координат, часто имеют причудливый вид и мало информативны. Поэтому используют для отображения функций, заданных в параметрическом виде, шаблоны декартовых графиков. Рассмотрим такой пример. 2. Построим графики двух параметрических функций x(t) = 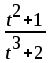 , y(t) = , y(t) = 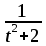 в полярной системе координат (рис.4.5), параметр t меняется в пределах 0 ÷ 360 deg, где deg – встроенная в MathCAD функция, означающая один градус. Для сравнения покажем графическую зависимость y(t) от x(t). в полярной системе координат (рис.4.5), параметр t меняется в пределах 0 ÷ 360 deg, где deg – встроенная в MathCAD функция, означающая один градус. Для сравнения покажем графическую зависимость y(t) от x(t).  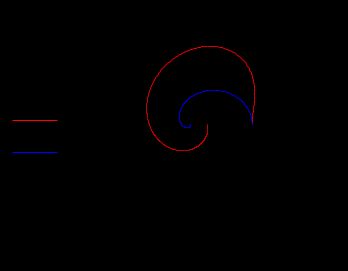  Рис. 4.5 Еще одной возможностью при работе с 2D графиками является применение специального графического маркера в виде двух перекрещивающихся пунктирных линий. Они появляются при выполнении операции Trace (Трассировка) во всплывающем меню форматирования графиков. При этом в появившемся окне операции будут отображаться координаты точки, в которой в данный момент находится маркер (см. рис.4.6). . 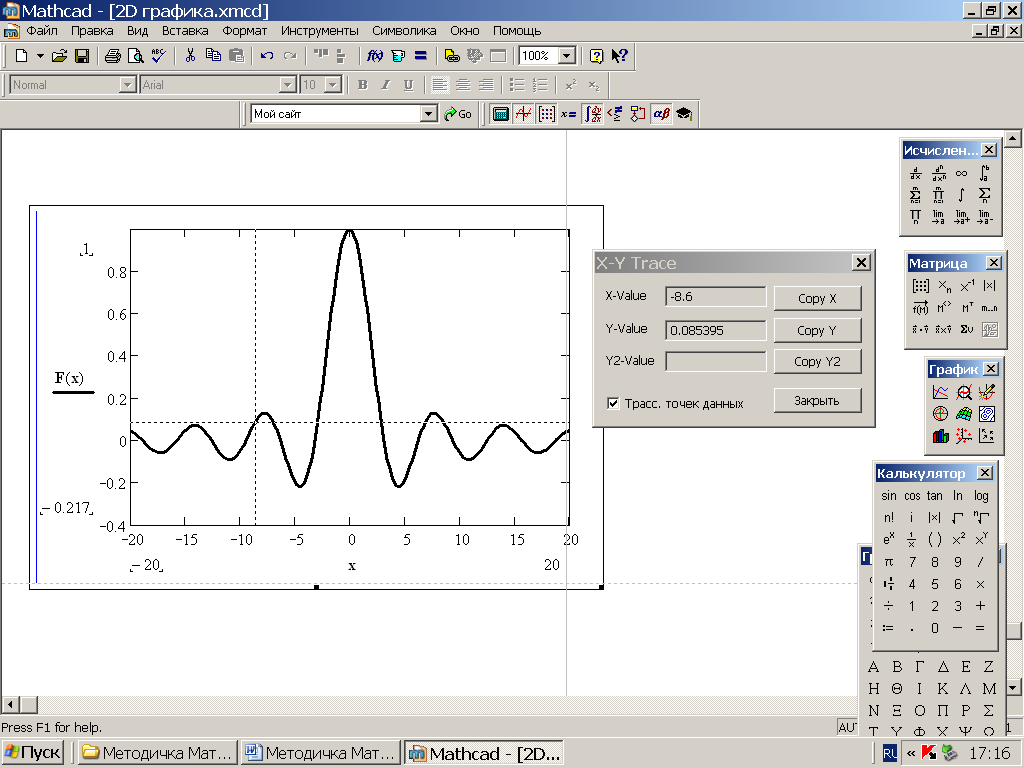 Рис.4.6 |
