Тема Механические свойства и их характеристики
 Скачать 399.59 Kb. Скачать 399.59 Kb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 вариант | А – В | | 5 вариант | О – Р |
| 2 вариант | Г – Е | | 6 вариант | С – У |
| 3 вариант | Ж – К | | 7 вариант | Ф – Ч |
| 4 вариант | Л – Н | | 8 вариант | Ш – Я |
Диаграммы растяжения по вариантам приведены ниже.
| Вариант 1 (сплав АМг3) |
 Нагрузка, кН 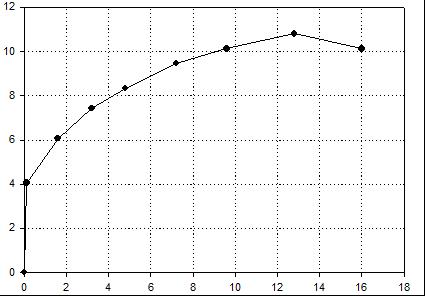 |
| Удлинение, мм |
| Номер точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Координаты точки | F, кН | 4,05 | 6,075 | 7,425 | 8,325 | 9,45 | 10,12 | 10,80 | 10,12 |
| Δl, мм | 0,12 | 1,6 | 3,2 | 4,8 | 7,2 | 9,6 | 12,8 | 16 | |
| Вариант 2 (сплав ВТ5) |
 Нагрузка, кН 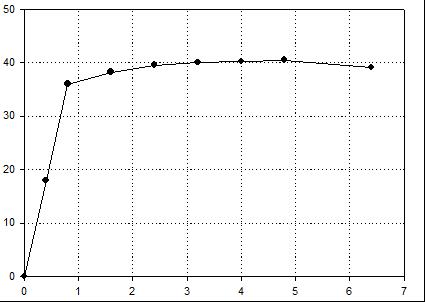 |
| Удлинение, мм |
| Номер точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Координаты точки | F, кН | 18,00 | 36,00 | 38,25 | 39,60 | 40,05 | 40,275 | 40,50 | 39,15 |
| Δl, мм | 0,4 | 0,8 | 1,6 | 2,4 | 3,2 | 4 | 4,8 | 6,4 | |
| Вариант 3 (сплав Ст2) |
 Нагрузка, кН 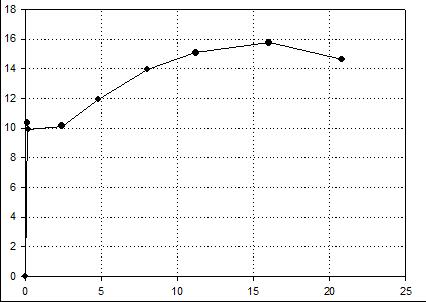 |
| Удлинение, мм |
| Номер точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Координаты точки | F, кН | 10,35 | 9,90 | 10,125 | 11,925 | 13,95 | 15,075 | 15,75 | 14,625 |
| Δl, мм | 0,12 | 0,2 | 2,4 | 4,8 | 8 | 11,2 | 16 | 20,8 | |
| Вариант 4 (сплав Ст4) |
 Нагрузка, кН 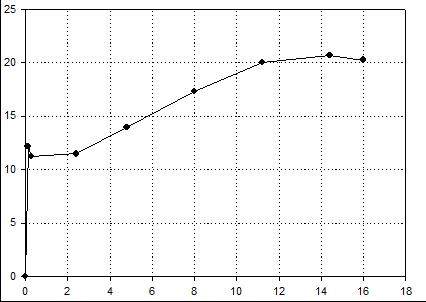 |
| Удлинение, мм |
| Номер точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Координаты точки | F, кН | 12,15 | 11,25 | 11,475 | 13,95 | 17,325 | 20,025 | 20,07 | 20,25 |
| Δl, мм | 0,12 | 0,28 | 2,4 | 4,8 | 8 | 11,2 | 14,4 | 16 | |
| Вариант 5 (сплав Д16) |
 Нагрузка, кН 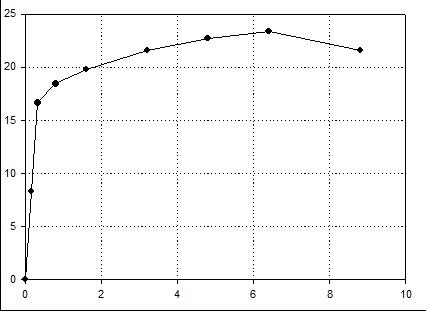 |
| Удлинение, мм |
| Номер точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Координаты точки | F, кН | 8,325 | 16,65 | 18,45 | 19,80 | 21,60 | 22,725 | 23,40 | 21,60 |
| Δl, мм | 0,16 | 0,32 | 0,8 | 1,6 | 3,2 | 4,8 | 6,4 | 8,8 | |
| Вариант 6 (сплав Х18Н10Т) |
 Нагрузка, кН 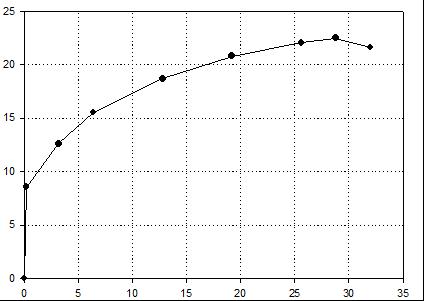 |
| Удлинение, мм |
| Номер точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Координаты точки | F, кН | 8,55 | 12,60 | 15,525 | 18,675 | 20,925 | 22,05 | 22,50 | 21,60 |
| Δl, мм | 0,18 | 3,2 | 6,4 | 12,8 | 19,2 | 25,6 | 28,8 | 32 | |
| Вариант 7 (сталь 80) |
 Нагрузка, кН 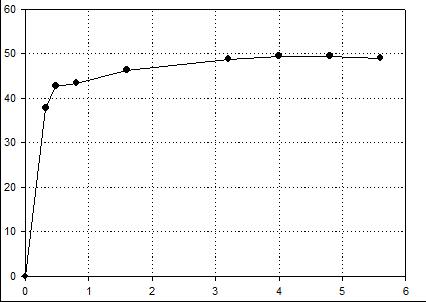 |
| Удлинение, мм |
| Номер точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Координаты точки | F, кН | 37,80 | 42,75 | 43,425 | 46,35 | 48,825 | 49,50 | 49,50 | 49,05 |
| Δl, мм | 0,18 | 3,2 | 6,4 | 12,8 | 19,2 | 25,6 | 28,8 | 32 | |
| Вариант 8 (сплав 14Г) |
 Нагрузка, кН 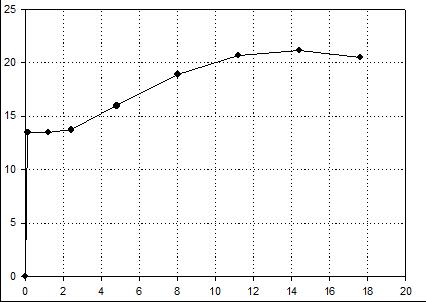 |
| Удлинение, мм |
| Номер точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Координаты точки | F, кН | 13,50 | 13,50 | 13,725 | 15,975 | 18,90 | 20,70 | 21,15 | 20,50 |
| Δl, мм | 0,12 | 1,2 | 2,4 | 4,8 | 8 | 11,2 | 14,4 | 17,6 | |
Рекомендации по выполнению задания
Чтобы преобразовать диаграмму «F–» в диаграмму «–» необходимо для ряда точек на первичной кривой провести расчет значений и ε. Для этого данные по усилию «F» разделить на площадь исходного поперечного сечения образца (S = 45 мм2), а по удлинению «» – разделить на исходную длину (l0 = 80 мм):
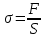 ,
, 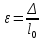 .
.Необходимо учитывать, что при расчете необходимо использовать единую систему единиц измерения. Поэтому S, равную 45 мм2, нужно перевести в м2 и выразить единицы измерения для напряжений в МПа. σ = F(кН) / S(м2) = … (МПа).
Полученные данные занести в таблицу.
Строго в масштабе построить кривую в координатах «–». По оси абсцисс располагать значения «». Масштаб выбрать таким, чтобы диаграмма была подробной и заполняла весь лист.
Модуль нормальной упругости рассчитать по первой точке.
Предел пропорциональности выбрать как максимальное значение напряжения, до которого сохраняется закон Гука.
Если на диаграмме растяжения присутствует площадка текучести, то определяется физический предел текучести
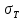 – наименьшее напряжение на площадке текучести.
– наименьшее напряжение на площадке текучести.При отсутствии площадки текучести определяют условный предел текучести
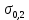 .
. 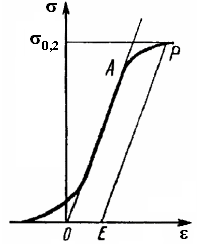 | Для этого из начала координат O по оси деформации откладывается отрезок OE, соответствующий величине деформации 0,2 %, или 0,002 относительной единицы деформации (рис. 1). Из точки E проводят прямую EP, параллельную OA. Точка пересечения прямой EP с диаграммой соответствует напряжению условного предела текучести. |
| Рис. 1. К определению величины условного предела текучести |
Предел упругости определяют аналогично условному пределу текучести. Разница только в величине остаточной деформации – 0,05 %, или 0,0005 отн. ед. (отрезок ОЕ).
Предел прочности, или временное сопротивление разрыву,
 – напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению образца.
– напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению образца.Относительное удлинение после разрыва представляет собой отношение приращения расчетной длины образца к его первоначальной длине, выраженное в процентах:
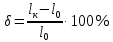 .
.Не имея образца, относительное удлинение можно примерно оценить по диаграмме. Для этого из конечной точки кривой, соответствующей моменту разрушения образца, провести прямую, параллельную прямолинейному участку диаграммы. Отрезок абсциссы, отсеченный этой прямой, будет соответствовать конечному относительному остаточному удлинению образца к. Этот результат нужно выразить в процентах:

Определить величину модуля пластичности можно, упростив диаграмму растяжения. Соедините предел текучести и предел прочности на кривой растяжения. Тангенс угла наклона прямой АВ пропорционален модулю пластичности: D tg . Расчет проводят по формуле
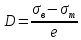 .
.Значение «е» определяет величину деформации, в процессе накопления которой напряжения выросли от σт до σв (рис.2).
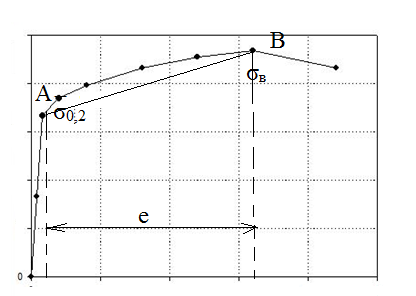 |
| Рис.2. К определению модуля пластичности |

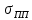 – предел пропорциональности;
– предел пропорциональности; 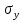 (
(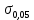 ) – предел упругости (предел пропорциональности можно отнести и к прочностным характеристикам).
) – предел упругости (предел пропорциональности можно отнести и к прочностным характеристикам).