Тесты-математика-Логика-УЧИТЬ. Тема Множества и операции над ними
 Скачать 331.65 Kb.
|
с) х>2их>530) Какое из высказываний истинно а) для того, чтобы число делилось на 3, необходимо, чтобы оно делилось на Ь  ) для того, чтобы число делилось на 3, необходимо и досгаточно, чтобы оно делилось на бс) для того, чтобы число делилось на 3, достаточно, чтобы оно делилось на Тема 4. Математическое доказательство Цель: Проверить знание понятий данной темы: умозаключение, посылка и заключение, дедуктивные (правильные) умозаключения, недедуктивные (неправильные) умозаключения, схемы дедуктивных умозаключений, прямое доказательство, косвенное доказательство, полная индукция и метод математическоЙ индукции. Проверить умение пользоваться соответствующей символикой и применять знания и умения для решения практических задач. Тесты составлены по следующим темам: — Умозаключения и их виды. — Схемы дедуктивных умозаключений. — Способы математического доказательства. Умозаключение— это а  ) логическая операция, раскрывающая содержание понятияЬ) повествовательное предложение, о котором можно сказать истинно оно или ложно с) логическая операция, посредством которой из одного или нескольких утверждений получается новое по отношению к исходным утверждение Умозаключение состоит из посылок и заключения а) нет Ь) да З) Какая из схем является правилом дедуктивного умозаключения? а)  Ща) Ь   )  Ща )с)  Как называется умозаключение, в котором между посылками и заключением имеет место отношение логического следования? а) недедуктивное умозаключение Ь) дедуктивное умозаключение Используя правило отрицания, выделите частную посылку Ща) в умозаключении: «Если число х четное, то оно делится на 2; число 15 не делится на 2, значит число 15 нечетное» а) число х четное, то оно делится на 2 Ь) число 15 не делится на 2 с) значит число 15 нечетное  Используя правило заключения, закончите умозаключение так, чтобы оно было дедуктивным: «Все имена собственные пишутся с большой буквы, Москва .»а) - имя собственное, следовательно, пишется с большой буквы Ь) пишется с большой буквы, следовательно, это имя собственное с) - столица России, поэтому пишется с большой буквы Какова схема данного умозаключения: «Все целые числа являются рациональными. Все рациональные числа являются действительными. Следовательно, все целые числа являются действительными» 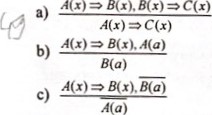 Какое умозаключение называют недедупивным? а) недедуктивное умозаключение - это способ получения нового знания на основе некоторых имеющихся Ь) недедуктивное умозаключение - это высказывание, содержащее новые знания с) недедуктивное умозаключение - это умозаключение, в котором между посылкой и заключением нет отношения логического следования Может ли быть истинный вывод в недедуктивном умозаключении? а) нет Ь) да Является ли правильным умозаключение: «В любом прямоугольнике диагонали равны В четырехугольнике АВСГ) диагонали равны, следовательно, четырехугольник АВС[) — прямоугольник?» а) да Ь) нет  1) Укажите схему недедуктивного умозаключенияа) А(х) В(х), Ща) ща) Ь) А(х) В(х), Ща) Ща) с)  Используя правило заключения, выделите общую посылку (см. справа) А(х) В(х) в умозаключении: «Все млекопитающие кормят детенышей молоком, лось — млекопитающее, значит, лось кормит детенышей молоком» а) лось млекопитающее Ь) значит, лось кормит детенышей молоком с) все млекопитающие кормят детенышей молоком Расположите предложения так, чтобы получилось правильное умозаключение: А 1 — отрезки АВ и имеют разные длины; А2 — отрезки АВ и СГ) неравны; АЗ — равные отрезки имеют равную длину 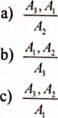 Утверждения, которые принимаются без доказательства, называются а) определениями Ь) аксиомами с) теоремами Примером прямого способа ведения математического доказательства является а) дедуктивный вывод Ь) метод математической индукции с) доказательство методом от противного Примером косвенного способа ведения математического доказательства является а) доказательство методом от противного Ь) дедуктивный вывод с) метод математической индукции Дедуктивный вывод — это а) способ математического доказательства, при котором истинность утвержден ия следует из истинности его во всех частных случаях  Ь) способ математического доказательства, который представляет собой такую цепочку дедуктивных умозаключений, что заключение каждого из них, кроме последнего, является посылкой в одном из после.ющих умозаключенийс) такое рассуждение, при котором на основании того, что некоторые объекты совокупности обладают определенным свойством, делается вывод о том, что этим свойством обладают все объекты этой совокупности. Примером особого способа ведения математического доказательства является а) доказательство методом от противного Ь) метод математической индукции с) дедуктивный вывод Если АО) и (МК) А(К+1)) — истинное высказывание, то делают вывод о том, что утверждение А (п) истинно для любого натурального числа п. Так формулируется: а) метод математической индукции Ь) дедуктивный вывод с) метод полной индукции Метод математической индукции состоит а) из одной части Ь) из п частей с) из двух частей Индукция — это метод рассуждений, ведущий от а) от общего к частному Ь) частных случаев к общему выводу Полная индукция — это а) способ математического доказательства, при котором истинность утверждения следует из истинности его во всех частных случаях Ь) способ математического доказательства, который представляет собой такую цепочку дедуктивных умозаключений, что заключение каждого из них, кроме последнего, является посылкой в одНоМ из последующих умозаключений с) такое рассуждение, при котором на основании того. что некоторые Обьекты совокупности обладают определенным свойством, делается вывод о том, что этим свойством обладают все (Бьекгы этой совокупности. ()TBeTb1 K recraM Testa 1. MH0*ecrBa onepat1HH Haa HUM"
Testa 2. MareMaTHqecKue n0HRTUg
Testa 3. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||