Тесты-математика-Логика-УЧИТЬ. Тема Множества и операции над ними

• Название: Тема Множества и операции над ними
• Дата: 16.03.2022
• Размер: 331.65 Kb.
• Имя файла: Тесты-математика-Логика-УЧИТЬ.docx
• Тип: Тесты; #399088
• страница: 1 из 6

Тема 1. Множества и операции над ними

Ц ель: Проверить знание понятий данной темы (множество, элемент множества, характеристическое свойство элементов множества), отношений между множествами, операций над множествами и свойств этих операций, умение пользоваться соответствующей символикой и применять знания и умения для решения практических задач.

Тесты составлены по следующим темам:

Понятие множества и элемента множества.

— Способы задания множеств.

Отношения между множествами.

— Пересечение множеств.

Объединение множеств.

— Вычитание множеств. Дополнение множества. — Декартово произведение множеств.

1. 
   Одним из основных (неопределяемых) понятий математики является
   

а) множество

Ь) функция

с) аксиома

2. 
   Множества принято обозначать
   

а) строчными буквами латинского алфавита а, Ь, с, ..., z Ь) прописными буквами латинского ифавита А, В, C...,Z

с) прописными буквами русского алфавита А, Б, В, Г...,Я

З) А — множество решений уравнения Сколько элементов содержит

это множество?

а) два Ь) один

с) ни одного

4) Пусть А — множество натуральных чисел, кратных 9. Какое из утверждений верно?

а) ПЕА

Ь) —18eA

с) Зея

5) Характеристическое свойство — это такое свойство

а) которым обладают некоторые элементы, принадлежащие множеству

Ь) которое характерно для данного множества

с) которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит

б) Укажите характеристическое свойство элементов множества А = {2, 3, 5, 7}

а) «быть простым однозначным числом»

Ь) «быть нечетным однозначным числом»

с) «быть нечетным числом»

7) Можно ли перечислить элементы множества

а) нет Ь) да

Множество В является подмножеством множества А если

а) каждый элемент множества А является также элементом множества В Ь) во множестве В есть такие же элементы, как и во множестве А

с) каждый элемент множества В является также элементом множества А

) Множества А и В называют равными, если

а) АсВиВсА

с) Каждому элементу множества А соответствует единственный элемент из множества В и наоборот

10. 
    Установите, в каком отношении находятся множества А и В, изображенные на рисунке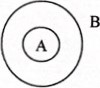
    

а) АсВ Ь) ВСА

10. 
    В каком отношении находятся множегва А — множество четных чисел, В — множество чисел, кратных четырем?
    

Ь) ВСА

с) Ас:В

7

10. 
    Определите отношение между множествами А и В, где А - множество параллелограммов, В — множество прямоугольников
    

а) в) с)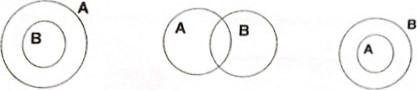

10. 
    Установите, в каком отношении ниодятся множества А и В, если А — множество четных чисел, В — множество чисел, кратных 2
    

а) АсВ Ь) ВСА

10. 
    Пересечением множеств А и В называется
    

а) множество, элементы которого принадлежат множеству А и множеству В Ь) множество, элементы которого принадлежат множеству А и не принадлежат множеству В

с) множество, элементы которого принадлежат или множеству А или множеству В

10. 
    Объединением множеств А и В называется
    

а) множество, элементы которого принадлежат множеству А и множеству В

Ь) множество, элементы которого принадлежат или множеству А или множеству В

с) множество, элементы которого принадлежат множеству А и не принадлежат множеству В

10. 
    Разностью множеств А и В называется
    

а) множество, элементы которого принадлежат множеству А и не принадлежат множеству В

Ь) множество, элементы которого принадлежат или множеству А или множесгву В

с) множество, элементы которого принщиежат множеству А и множеству В

17) Пусть В с А. Дополнением множества В до множества А называется

а) множество, элементы которого принадлежат или множеству А или множесгву В

Ь) множество. элементы которого принадлежат множеству А и не принадлежат множеству В

с) множество, элементы которого принщиежат множеству А и множеству В

18) Среди следующих высказываний установите истинное