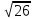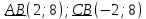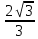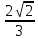тест. тест выход. Тема Особенности методики обучения решению текстовых задач (на проценты, на работу, на движение, на пропорции, на смеси и сплавы)
 Скачать 45.03 Kb. Скачать 45.03 Kb.
|
|
Банк тестовых заданий Тема 1.2. Особенности методики обучения решению текстовых задач (на проценты, на работу, на движение, на пропорции, на смеси и сплавы). Задание 1. Методика обучения решению текстовых задач (на проценты, на работу, на пропорции, на смеси и сплавы). Вопрос 1: Товар на распродаже уценили на 30%, при этом он стал стоить 840 тенге. Сколько тенге стоил товар до распродажи?
Вопрос 2: В начале года число абонентов телефонной компании “Казахтелеком” составляло 500 тысяч человек, а в конце года их стало 575 тысяч человек. На сколько процентов увеличилось за год число абонентов этой компании? Правильный ответ
Вопрос 3: Акции предприятия распределены между государством и частными лицами в отношении 3 : 2. Общая прибыль предприятия после уплаты налогов за год составила 11 млн тенге. Какая сумма (в тенге) из этой прибыли должна пойти на выплату частным акционерам? Правильный ответ
Вопрос 4: В ответ запишите, чему равен х 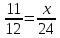 Правильный ответ
Вопрос 5: Спортивный магазин проводит акцию. Любая футболка стоит 200 тенге. При покупке двух футболок - скидка на вторую футболку 50%. Сколько тенге придется заплатить за покупку двух футболок в период действия акции? Правильный ответ
Задание 2. Методы и приемы решения текстовых задач. Вопрос 1: Двое рабочих выполняют некоторую работу. После 45 минут совместной работы первый рабочий был переведен на другую работу, и второй рабочий закончил оставшуюся часть работы за 2 часа 15 минут. За какое время мог бы выполнить работу каждый рабочий в отдельности, если известно, что второму для этого понадобится на 1 час больше, чем первому. Правильный ответ
Вопрос 2: Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа? Правильный ответ
Вопрос 3: Двое рабочих выполнили работу за два дня. Если бы первый рабочий проработал 2 дня, а второй 1 день, то они вместе выполнили бы всей работы. За сколько дней выполнит эту работу первый рабочий? Правильный ответ
Вопрос 4: Ученик прочел книгу в 480 страниц, ежедневно читая одинаковое количество страниц. Если бы он читал каждый день на 16 страниц больше, то прочел бы книгу на 5 дней раньше. Сколько дней ученик читал книгу? Правильный ответ
Вопрос 5: Вася с Колей мастерят из бумаги кораблики. Вася может сделать за 1 час 15 корабликов, а Коля только 10. Сколько времени им потребуется на 100 корабликов? Правильный ответ
Задание 3. Проектирование фрагмента урока для обучения решению текстовых задач. Вопрос 1: Пароход прошел 10 км против течения реки, а затем прошел еще 45 км по течению, затратив на весь путь два часа. Найдите собственную скорость парохода, если скорость течения реки равна 5 км/ч. Правильный ответ
Вопрос 2: Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. Правильный ответ
Вопрос 3: Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть - со скоростью 16 км/ч, а последнюю треть — со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч. Правильный ответ
Вопрос 4: Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 30 секунд. Найти длину поезда в метрах. Правильный ответ
Вопрос 5: Расстояние между двумя городами скорый поезд проходит на 4 часа быстрее товарного и на 1 час быстрее пассажирского. Найти скорости товарного и скорого поездов, если известно, что скорость товарного поезда составляет 5/8 от скорости пассажирского и на 50 км/ч меньше скорости скорого. Правильный ответ
Тема 1.3. Методы обучения решения текстовых задач с помощью дробно-рациональных и квадратных уравнений. Задание 1. Методы обучения решения текстовых задач с помощью дробно-рациональных уравнений. Вопрос 1: Автобус-экспресс отправляется от вокзала в аэропорт, находящийся на расстоянии 120 км от вокзала. Пассажир, опоздавший на 10 минут на автобус, решил добраться до аэропорта на такси. Скорость такси на 10км/ч больше скорости автобуса. С какой скорость ехал автобус, если он приехал в аэропорт одновременно с такси? Правильный ответ
Вопрос 2. От посёлка до речки 60 км. Утром турист на скутере отправился на речку. Вечером он возвратился в посёлок, но при этом ехал со скоростью на 10 км/ч меньшей и потратил на дорогу на 18 мин больше. Сколько времени ехал турист от речки к посёлку? Правильный ответ
Вопрос 3. Катер прошёл по течению 120 км. На этот же путь против течения от тратит времени в 1,5 раза больше. Найдите скорость течения, если скорость катера в стоячей воде 20 км/ч. Правильный ответ
Вопрос 4. В раствор, содержащий 50 г соли, добавили 150 г воды. В результате концентрация соли уменьшилась на 7,5%. Найдите первоначальную массу раствора. Правильный ответ
Вопрос 5. Мастер и его ученик, работая вместе, выполняют норму на 8 ч. Если каждый работает самостоятельно, то мастер тратит на выполнение нормы на 12 ч меньше, чем ученик. Сколько часов тратит каждый из них на выполнении нормы? Правильный ответ
Задание 2. Методы обучения решения текстовых задач с помощью квадратных уравнений. Вопрос 1. В квартире проектируется две комнаты одинаковой ширины. Длина первой комнаты в 1,5 раза больше её ширины, а длина второй комнаты 7,2 м. Определите, какой ширины должны быть комнаты, если общая их площадь может быть 56,7м2? Правильный ответ
Вопрос 2. В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе, если известно, что радиус Земли равен 6380 км. Какую высоту должна иметь вышка мобильной связи, поставленная в нашем городе, чтобы село Бутаково и Черемшанка попали в зону связи (расстояние от вышки до данных сел по прямой не больше 25 км.)? Правильный ответ
Вопрос 3. Найдите двузначное число, если цифра его десятков на 2 больше цифры единиц, а произведение числа и суммы его цифр равно 900. Правильный ответ
Вопрос 4. В период военных учений в системе обороны дивизии было создано несколько командных пунктов, причем каждый из них имел линию связи с любым другим из числа оставшихся. Сколько командных пунктов организовано, если количество линий связи равно 45? Правильный ответ
Вопрос 5. В однокруговом шахматном турнире было сыграно 78 партий. Сколько человек участвовало в соревновании? Правильный ответ
Тема 1.4. Методика обучения решению уравнений с переменной под знаком модуля (например: |ax2+bx|+c=0, ax2+b|x|+c=0). Задание 1. Методы обучения решения уравнений с переменной под знаком модуля: (например: |ax2+bx|+c=0, ax2+bх+с=0). Вопрос 1. Решить уравнение: 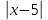 =3 =3Правильный ответ
Вопрос 2. Решить уравнение: 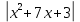 =3 =3Правильный ответ
Вопрос 3. Решить уравнение: 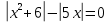 Правильный ответ
Вопрос 4. Решить уравнение: 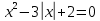 Правильный ответ
Вопрос 5. Решить уравнение: 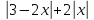 =3 =3 Правильный ответ
Задание 2. Методы обучения решения уравнений с переменной под знаком модуля (например: ax2+bх+с=0, ax2+b|x|+c=0) различными способами. Вопрос 1. Решите уравнение 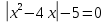 Правильный ответ
Вопрос 2. Решите уравнение 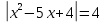 А. -1;5 Правильный ответ
Вопрос 3. Решите уравнение 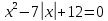 Правильный ответ
Вопрос 4. Решите уравнение 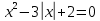 Правильный ответ
Вопрос 5. Решите уравнение 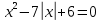 Правильный ответ
Задание 3. Проектирование фрагмента урока для обучения решению уравнений с переменной под знаком модуля (например: |ax2+bx|+c=0, ax2+b|x|+c=0). Вопрос 1. Решите уравнение: 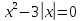 Правильный ответ
Вопрос 2.Решите уравнение: 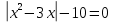 Правильный ответ
Вопрос 3. Решите уравнение: x2-5|х|= 0. Правильный ответ
Вопрос 4. Решите уравнение: x² - 3|x| + 2 = 0 Правильный ответ
Вопрос 5. Решите уравнение: x2 – 6|x| + 5 = 0 Правильный ответ
Тема 1.5. Построение графиков линейной и квадратичной функции с использованием различных графических редакторов Задание 1. Построение графиков линейной и квадратичной функции с использованием электронной таблицы Excel Вопрос 1: Функция задана формулой у = 0,7х - 3,5. Найдите координаты точки пересечения графика этой функции с осью абсцисс. Правильный ответ
Вопрос 2: Функция задана формулой у = -2х - 7. Найдите координаты точки пересечения графика этой функции с осью ординат. Правильный ответ
Вопрос 3: Какая из точек А (3 : -3) и В (1; 5) принадлежит графику функции у = -4х + 9? Правильный ответ
Вопрос 4: Задайте формулой прямую пропорциональность, график которой проходит через точку А (-2; 8) Правильный ответ
Вопрос 5: Функция задана формулой у = -6х + b. График этой функции проходит через точку А(2; -9). Найдите b: Правильный ответ
Задание 2. Построение графиков линейной и квадратичной функции с использованием динамической среды GeoGebra. Вопрос 1. Пользуясь определением квадратичной функции, из данных функций выберите квадратичные: Правильный ответ
Вопрос 2. Дана функция 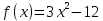 . Найти f(-2). Запишите ответ: . Найти f(-2). Запишите ответ: Правильный ответ
Вопрос 3. Найдите промежуток возрастания функции 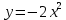 +7x-3 +7x-3 Правильный ответ
Вопрос 4. Найдите точки пересечения парабол 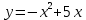 и и 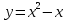 . В ответ укажите наибольшую ординату. . В ответ укажите наибольшую ординату.Правильный ответ
Вопрос 5. Укажите координаты вершины параболы у=х2-4х +7 Правильный ответ
Задание 3. Преобразование графиков линейной и квадратичной функции. Вопрос 1. Функция задана формулой у= 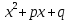 . Найди p и q, если график функции проходит через точки (1;2) и (0;3) . Найди p и q, если график функции проходит через точки (1;2) и (0;3)Правильный ответ
Вопрос 2. Задайте формулой квадратичную функцию, график которой проходит через точки А(-3;3), В(1;3), С(-4;8) Правильный ответ
Вопрос 3. Функция задана формулой у= 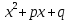 . Найди p и q, если наименьшее значение равное 1, функция принимает при х=-3 . Найди p и q, если наименьшее значение равное 1, функция принимает при х=-3Правильный ответ
Вопрос 4. Определите значение х, при котором функция у= 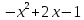 принимает наибольшее значение. Найдите это значение принимает наибольшее значение. Найдите это значениеПравильный ответ
Вопрос 5. Определите значение х, при котором функция у=- 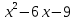 принимает наибольшее значение. Найдите это значение принимает наибольшее значение. Найдите это значениеA. х=3; у=-4 Правильный ответ
Тема 1.6. Элементы комбинаторики. Решение задач с использованием формул комбинаторики. Бином Ньютона и его свойства Задание 1. Элементы комбинаторики. Решение задач с использованием формул комбинаторики. Вопрос 1.В гардеробе ученика есть 3 рубашки и 5 футболок. Сколько существует вариантов выбрать одежду для прогулки? Правильный ответ
Вопрос 2.В гардеробе ученицы есть 3 платья и 5 пар туфель. Сколько всего есть вариантов выбрать платье и туфли? Правильный ответ
Вопрос 3. Сколькими способами можно расставить 8 томов энциклопедии на книжной полке так, чтобы первый и второй тома стояли рядом? Правильный ответ
Вопрос 4. Решите уравнение: 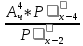 =42 =42Правильный ответ
Вопрос 5. В генетическом Эксперименте 4 белых, 7 красных, 5 розовых цветков гороха были взяты из имеющихся 10 белых, 10 красных, 10 розовых. Сколькими способами можно это сделать? Правильный ответ
Задание 2. Бином Ньютона и его свойства. Вопрос 1. Найти наибольший член при разложении 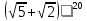 Правильный ответ
Вопрос 2. 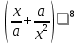 в разложении. Найти член при в разложении. Найти член при 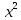 Правильный ответ
Вопрос 3. Школьные туристы решили совершить путешествие к горному озеру. Первый этап пути можно преодолеть на поезде или автобусе. Второй этап - на байдарках, велосипедах или пешком. И третий этап пути - пешком или с помощью канатной дороги. Какие возможные варианты путешествия есть у школьных туристов? Правильный ответ
Вопрос 4. В кружок бального танца записались Петя, Коля, Витя, Игорь, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться? Правильный ответ
Вопрос 5. Запишите трехзначные числа, которые можно составить из цифр 1, 9, 6 используя в записи числа каждую из них не больше одного раза. В ответе укажите большее из них. Правильный ответ
Задание 3. Проектирование фрагмента урока по решению задач с использованием формул комбинаторики и бинома Ньютона. Вопрос 1. Сколько может быть различных комбинаций выпавших граней при бросании двух игральных костей? Правильный ответ
Вопрос 2. Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 2, 4, 6? Правильный ответ
Вопрос 3.Сколько всего исходов, если бросают одну и ту же монету два раза? Правильный ответ
Вопрос 4. Имеется 9 различных книг, 4 из которых — учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом? Правильный ответ
Вопрос 5. В корзине лежат 8 белых шаров и 12 черных. Сколькими способами можно достать из этой корзины 2 белых шара и 2 черных? A Правильный ответ
Тема 1.7. Последовательности. Метод математической индукции. Задание 1. Последовательности. Вопрос 1. По данной формуле числовой последовательности an=3n определить ее четвертый член. Правильный ответ
Вопрос 2. Записать первые пять членов числовой последовательности с общим членом an=4n-9. Правильный ответ
Вопрос 3. Выпишите первые четыре члена последовательности {bn}, если b1=5; bn+1=bn+3. Правильный ответ
Вопрос 4. Определите правило составления числовой последовательности: 1; 4; 7; 10; 13; … Задайте формулой общий член этой последовательности. Правильный ответ
Вопрос 5. Дано: a1=-1; a2=3. Найдите третий член числовой последовательности, заданной рекуррентной формулой: an+2=2an+1+3an. Правильный ответ
Задание 2. Метод математической индукции. Вопрос 1. Найдите первые пять членов последовательностей ( 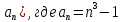 Правильный ответ
Вопрос 2. Найти первые пять членов последовательностей, n-й член которых выражается формулой 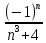 Правильный ответ
Вопрос 3. Найдите номер наибольшего члена последовательности ( 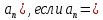 Правильный ответ Правильный ответ
Вопрос 4. Пусть дана последовательность (n) натуральных чисел. Найти формулу вычисления суммы первых n чисел: Правильный ответ
Вопрос 5. Пусть дана последовательность ( 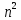 ) квадратов натуральных чисел. Найти формулу вычисления суммы первых n чисел: ) квадратов натуральных чисел. Найти формулу вычисления суммы первых n чисел: Правильный ответ
Тема 1.8. Применение метода координат на плоскости к решению задач. Применение векторов к решению задач. Задание 1. Методические рекомендации по применению метода координат на плоскости к решению задач. Вопрос 1. Даны точки А(0;-3), В(-1;0), С(5;2). Найдите координаты и длину вектора 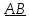 Правильный ответ
+2 Правильный ответ
Вопрос 3. Запишите уравнение окружности с центром в точке А и радиусом АВ Правильный ответ
Вопрос 4. Даны точки А(2;3), В(-2;0), С(2;-3). Запишите уравнение прямой, содержащей медиану СМ треугольника АВС Правильный ответ
Вопрос 5. Запишите уравнение окружности касающейся осей координат и проходящей через точку
Задание 2. Методические особенности применения векторов к решению задач. Вопрос 1. Даны векторы 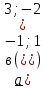 . Найдите координаты векторов m=-3 . Найдите координаты векторов m=-3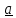 , n= , n=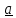 +2 +2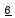 Правильный ответ
Вопрос 2. Запишите разложение векторов 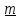 и и 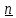 по координатным векторам i и j по координатным векторам i и j Правильный ответ
Вопрос 3. Найдите среди векторов 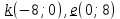 , , 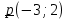 , , 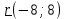 векторы, коллинеарные векторам векторы, коллинеарные векторам 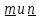 Правильный ответ
Вопрос 4. Даны точки А(-2;0), В(2;2). Найти координаты вектора АВ. Правильный ответ
Вопрос 5. Разложите векторы АВ по координатным векторам i и j Правильный ответ
Задание 3. Проектирование фрагментов уроков по решению задач на применение метода координат и векторов. Вопрос 1. Даны точки А(-2;3), В(2;0), С(-2;-3). Запишите уравнение прямой, содержащей медиану СМ треугольника АВС Правильный ответ
Вопрос 2. В треугольнике АВС МN средняя линия, М 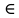 АВ, N АВ, N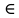 BC. Найдите координаты точек В и С, если А(-1;3), М(3;4), N(4;2). BC. Найдите координаты точек В и С, если А(-1;3), М(3;4), N(4;2).Правильный ответ
Вопрос 3. Найдите координаты точек В и С, если А(1;3) М(4;0) N(3;-2). MN средняя линия М 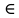 АВ, N АВ, N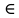 BC. Найдите длины медианы АN, CM BC. Найдите длины медианы АN, CMПравильный ответ
Вопрос 4. Даны точки А(1;-2) В(3;6) С(5;-2). Найдите координаты векторов 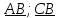 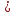 Правильный ответ
Вопрос 5. Даны точки А(1;2) В(3;6). Найдите координаты точки М, делящей пополам отрезок АВ Правильный ответ
Тема 1.9. Основные сложности при изучении тригонометрических функций острого угла в прямоугольном треугольнике. Решение треугольников. Задание 1. Основные сложности при изучении тригонометрических функций острого угла в прямоугольном треугольнике. Вопрос 1. Вычислите 2sin 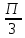 -tg -tg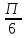 Правильный ответ
Вопрос 2. Вычислите cos2П+2сtg 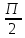 Правильный ответ
Вопрос 3. В прямоугольном треугольнике АВС угол С = 90 градусов, АС=8 см, а АВ на 2 см больше ВС. Найдите tg угла А. Правильный ответ
Вопрос 4. В треугольнике АВС угол С=90 градусов, угол В=56 градусов, ВС=7 см. Найдите АС. Правильный ответ
Вопрос 5. Треугольник СDК прямоугольный, угол С = 90 градусов, угол К = 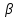 , СD = b, СМ , СD = b, СМ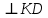 . Найти СМ. . Найти СМ.Правильный ответ
Задание 2. Методические особенности по обучению задач на решение треугольников. Вопрос 1. Дан прямоугольный треугольник FDC, угол С = 90°, sin F = 0,64. Найдите cos D Правильный ответ
Вопрос 2. В равнобедренном треугольнике АВС АВ = ВС = 10, АС = 5. Найдите cos A. Правильный ответ
Вопрос 3. В прямоугольном Δ АВС угол С прямой, СН - высота, АВ = 15, cos А = 0,6. Найти АН. Правильный ответ
Вопрос 4. Диагонали ромба равны 3 и 4. Найдите синус угла между большей диагональю и стороной ромба. 8 Правильный ответ
Вопрос 5. Найдите косинус угла при вершине равнобедренного Δ, если высота проведенная к боковой стороне меньше этой стороны в 3 раза. Правильный ответ
Задание 3. Проектирование фрагментов уроков на решение треугольников. Вопрос 1. Найдите сторону (в см) треугольника, если высота, опущенная на эту сторону, в 2 раза меньше нее, а площадь треугольника составляет 64 см. Правильный ответ
Вопрос 2. В ромбе M N P K известны длины диагоналей: MP=14 см, NK=9 см. На диагонали MP выбрана точка A так, что MA:AP=2:5. Найдите площадь треугольника APK (в 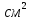 ). ).Правильный ответ
Вопрос 3. В треугольнике ABC проведены медианы AE и BP. Площадь треугольника ABC равна 36 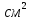 . Найдите площадь треугольника ABE (в . Найдите площадь треугольника ABE (в 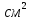 ). ).Правильный ответ
Вопрос 4. В треугольнике ABC проведены медианы AE и BP. Площадь треугольника ABC равна 36 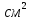 . Найдите площадь треугольника BРС (в . Найдите площадь треугольника BРС (в 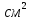 ). ).Правильный ответ
Вопрос 5. Сторона равностороннего треугольника равна 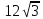 . Найдите радиус описанной около этого треугольника окружности. . Найдите радиус описанной около этого треугольника окружности.
|

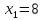 ,
, 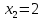
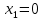 ,
, 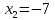 ,
, 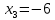 ,
, 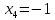
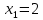 ,
, 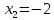 ,
, 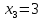 ,
, 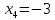
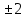 ,
, 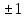
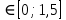
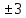 ;
; 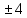
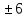 ;
; 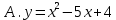 D
D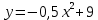
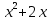
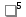
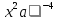
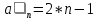
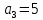
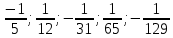
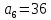
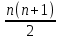
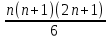
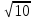
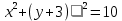
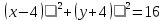
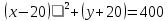
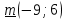 ;
; 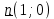
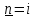
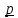
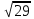 ;
;