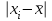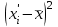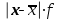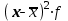статистика. Тема 5. Тема Показатели вариации Содержание задания и требования к нему

• Название: Тема Показатели вариации Содержание задания и требования к нему
• Анкор: статистика
• Дата: 25.04.2022
• Размер: 57.42 Kb.
• Имя файла: Тема 5.docx
• Тип: Документы; #495461

Тема 5. Показатели вариации
5.1. Содержание задания и требования к нему
В соответствии с вариантом задания темы 1 необходимо осуществить:

а) группировку предприятий по группировочному признаку;

б) рассчитать и представить в таблице по первой группе показатели: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации;

в) в соответствии с вариантом решить задачу.

Решение:

а) В табл. 5.1 приведена группировка предприятий объему реализованной продукции представлены в табл. 5.1
Таблица 5.1 Группировка предприятий по стоимости ОФ

Группы предприятий по стоимости реализованной продукции, млн. руб.	Код предприятия	Реализованная продукция, млн.руб.	ОПФ, млн.руб.	Среднесписочная численность работающих, чел.
1,5-6,7	45	1,5	1,1	174
	63	1,6	1,4	208
	78	1,7	1,3	215
	80	1,7	1,4	225
	49	1,9	1,6	333
	79	1,9	1,3	333
	47	2,2	1,2	349
	60	2,2	1,4	340
	46	2,3	1,9	295
	52	2,5	1,4	375
	76	2,6	1,5	383
	48	2,8	1,3	418
	69	3,0	1,8	419
	53	3,5	1,8	452
	65	3,6	2,3	456
	58	3,9	2,5	468
	59	3,9	2,2	457
	81	4,2	10,5	310
	57	4,4	2,8	493
	56	4,7	2,8	507
	77	4,9	2,5	578
	50	5,1	2,9	539
	51	5,2	2,8	566
	74	5,3	4,4	663
	73	5,9	4,8	673
	82	5,9	2,9	480
	72	6,1	5,8	718
	71	6,4	5,0	758
Итого	28	100,9	74,6	12185,0
6,7-11,9	70	6,7	5,5	772
	68	6,9	4,8	805
	54	7,1	5,5	811
	84	8,0	7,5	900
	55	8,7	6,8	864
	67	9,0	7,5	924
	66	10,3	9,1	1014
	83	11,0	9,5	1100
	64	11,5	9,7	1117
Итого	9	79,2	65,9	8307,0
11,9-17,1	75	16,2	12,2	1337
	61	17,0	18,1	1392
Итого	2	33,2	30,3	2729,0
17,1-22,3	62	22,3	17,4	1628
Итого	1	22,3	17,4	1628,0
Всего	40	235,6	188,2	24849,0

б) Размах вариации представляет собой разность между максимальным и минимальным значением признака исследуемой совокупности:

.

R=6,4-1,5=4,9 млн.руб.

Отклонение максимального объема реализации от минимального составило 4,9 млн.руб.

Средний объема реализации по формуле средней арифметической простой:



Среднее линейное отклонение – это средняя арифметическая абсолютных отклонений значений признака от среднего уровня: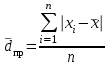

;

Сведем расчеты в табл. 5.2
Таблица 5.2 Расчетная таблица

Код предприятия	Реализованная продукция, млн.руб., х
45	1,5	2,104	4,425
63	1,6	2,004	4,014
78	1,7	1,904	3,624
80	1,7	1,904	3,624
49	1,9	1,704	2,902
79	1,9	1,704	2,902
47	2,2	1,404	1,970
60	2,2	1,404	1,970
46	2,3	1,304	1,699
52	2,5	1,104	1,218
76	2,6	1,004	1,007
48	2,8	0,804	0,646
69	3,0	0,604	0,364
53	3,5	0,104	0,011
65	3,6	0,004	0,000
58	3,9	0,296	0,088
59	3,9	0,296	0,088
81	4,2	0,596	0,356
57	4,4	0,796	0,634
56	4,7	1,096	1,202
77	4,9	1,296	1,681
50	5,1	1,496	2,239
51	5,2	1,596	2,549
74	5,3	1,696	2,878
73	5,9	2,296	5,274
82	5,9	2,296	5,274
72	6,1	2,496	6,232
71	6,4	2,796	7,820
Итого	100,9	38,107	66,690

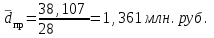Среднее линейное отклонение от средней арифметической составляет 1,361 млн.руб.

Дисперсия – это средняя из квадратов отклонений от средней арифметической: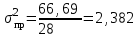




Квадрат отклонений объема реализованной продукции от средней составляет 2,382.

Среднеквадратическое отклонение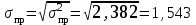

млн.руб.

Коэффициент вариации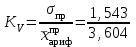

или 42,8%

Таким образом, исследуемая совокупность является неоднородной, т.к. коэффициент вариации составляет 42,8%. В среднем по исследуемой совокупности варианты отличаются от средней арифметической на 1,543 млн.руб.
Задача 10
Имеется следующий ряд распределения телеграмм, принятых отделением связи по числу слов:

Количество слов в телеграмме	Число телеграмм
12	18
16	22
14	34
15	26
16	20
17	13
18	7
ИТОГО	140

Рассчитать абсолютные и относительные показатели вариации.
Решение:

1. Для вычисления среднего количества слов в телеграмме применим формулу средней арифметической взвешенной:



где Х – количество слов в телеграмме;

f – число телеграмм.
Таблица 10.1 Расчетная таблица

Количество слов в телеграмме, Х	Число телеграмм, f	Х∙f
12	18	216	45,643	6,430	115,737
13	22	286	33,786	2,358	51,885
14	34	476	18,214	0,287	9,758
15	26	390	12,071	0,216	5,605
16	20	320	29,286	2,144	42,883
17	13	221	32,036	6,073	78,945
18	7	126	24,250	12,001	84,009
Итого	140	2035	195,286		388,821

Среднее количество слов в телеграмме составляет 14,5 слова.

2. Для расчета среднего линейного отклонения применим формулу: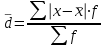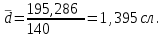





Количество слов в отдельной телеграмме в среднем по всей совокупности телеграмм отклонялось в ту и другую сторону от своего среднего значения на 1,4 слова.

Дисперсия определяется по следующей формуле: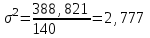





Вычислим среднее квадратическое отклонение: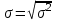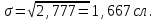





Количество слов каждой из 140 телеграмм отклонялись в ту и другую сторону от среднего значения на 1,7 слова.

3. Найдем коэффициент вариации:





Совокупность статистически однородная (11,5˂33).

Коэффициент осцилляции равен: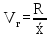



Размах вариации представляет собой разность между максимальным и минимальным значением признака исследуемой совокупности:



_{R=18-12=6 сл.}

Размер отклонений максимального количества слов в телеграмме от минимальной по всей совокупности телеграмм составляет 6 слов.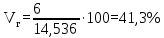



Колеблемость крайних значений количества слов отдельных телеграмм вокруг средней составляет 41,3%.

Относительное линейное отклонение:



Т.е. доля усредненного значения абсолютных отклонений количества слов в отдельных телеграммах от средней составляет 9,6%.

Таким образом, анализируемый вариационный ряд распределения телеграмм по количеству слов является статистически однородным, так как коэффициент вариации меньше 33%.

Среднее значение количества слов по данной совокупности телеграмм (14,5 сл.) является надежной или типической ее характеристикой.