|
|
сор 1. СОР1-Г-11-ЕМН. Тема Понятие многогранника
Геометрия, 11 класс, ЕМН
Суммативное оценивание за раздел «Многогранники»
Тема
|
Понятие многогранника
Призма и ее элементы, виды призм
Развертка, площадь боковой и полной поверхности призмы.
Пирамида и ее элементы. Правильная пирамида
|
Цель обучения
|
11.1.2 - знать определение многогранника и его элементов;
11.1.3 - знать определение призмы, ее элементов, виды призм; уметь изображать их на
плоскости;
11.1.11 - уметь выполнять развёртки многогранников и тел вращений;
11.3.3 - решать задачи на нахождение элементов многогранников;
11.3.1 - выводить формулы площади боковой и полной поверхности призмы и применять
их при решении задач;
- знать определение пирамиды, ее элементов, виды пирамид; уметь изображать их на плоскости;
11.2.4 - определять расположение проекции вершины пирамиды на плоскость основания;
|
Критерий оценивания
|
Обучающийся
Выполняет построение призмы на плоскости по ее развертке и определяет ее вид.
Решает задачи на нахождение элементов призмы и пирамиды.
Применяет формулы площади боковой и полной поверхности призмы при решении задач.
Определяет расположение проекции вершины пирамиды на плоскость основания.
|
Уровень мыслительных навыков
|
Знание и понимание
Применение
|
Время выполнения
|
30 минут
|
Задания.
Вариант 1
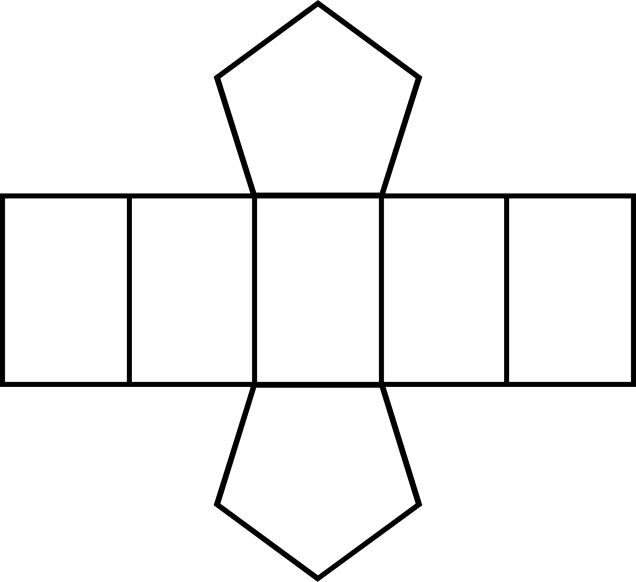 1. Постройте многогранник по его развертке и определите вид. 1. Постройте многогранник по его развертке и определите вид.
2. Длины диагоналей трех граней прямоугольного параллелепипеда, имеющих общую вершину, равны 6 см, 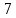 см и 9 см. Найдите диагональ параллелепипеда. см и 9 см. Найдите диагональ параллелепипеда.
3. Стороны основания прямой треугольной призмы равны 12 см, 13 см и 5 см, а боковое ребро равно большей высоте основания. Найдите площадь полной поверхности призмы.
4. Высота правильной четырехугольной пирамиды равна 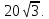 Боковое ребро наклонено к плоскости основания под углом 60°. Найди боковое ребро пирамиды. Боковое ребро наклонено к плоскости основания под углом 60°. Найди боковое ребро пирамиды.
Вариант 2
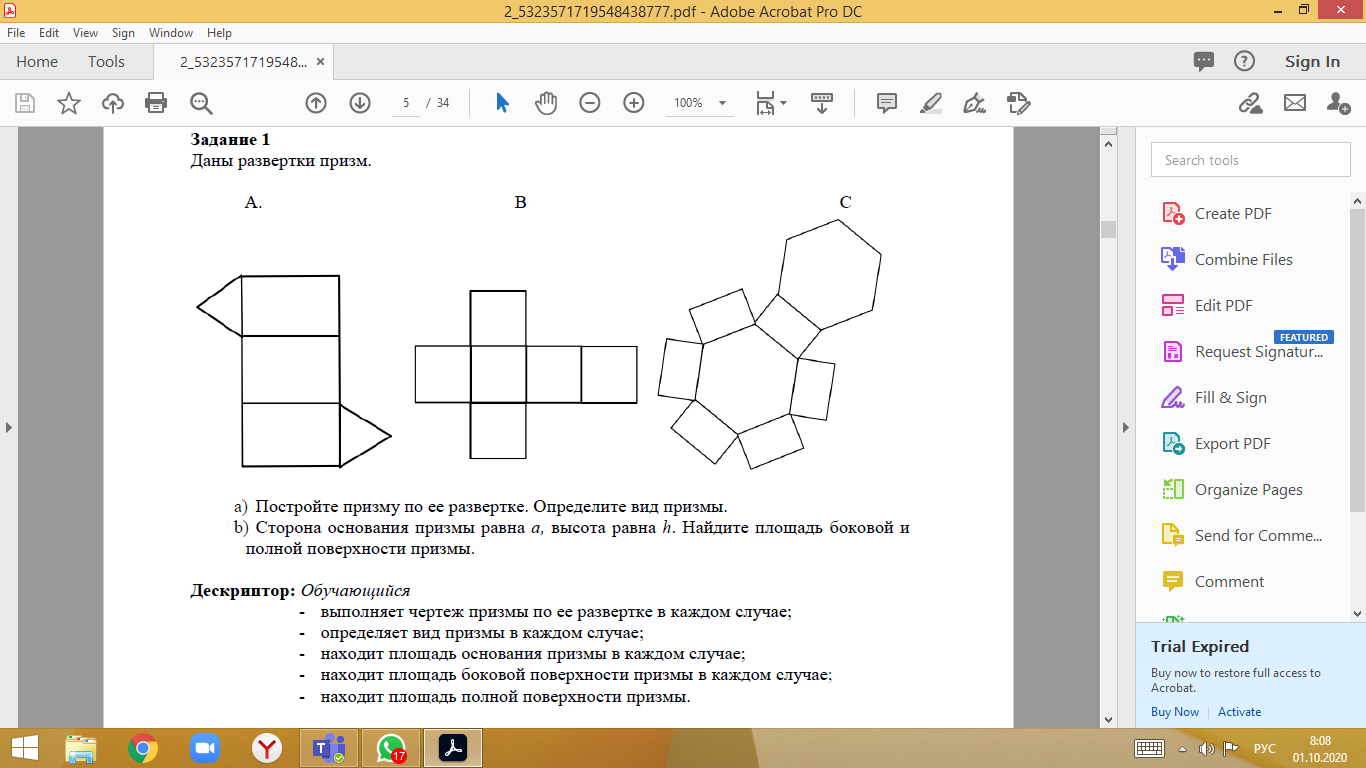 1. Постройте многогранник по его развертке и определите вид. 1. Постройте многогранник по его развертке и определите вид.
Длины диагоналей трех граней прямоугольного параллелепипеда, имеющих общую вершину, равны 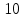 см, см, 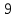 см и 8 см. Найдите диагональ параллелепипеда. см и 8 см. Найдите диагональ параллелепипеда.
Стороны основания прямой треугольной призмы равны 15 см, 17 см и 8 см, а боковое ребро равно большей высоте основания. Найдите площадь полной поверхности призмы.
4. Высота правильной четырехугольной пирамиды равна 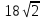 . Боковое ребро наклонено к плоскости основания под углом 45°. Найди боковое ребро пирамиды. . Боковое ребро наклонено к плоскости основания под углом 45°. Найди боковое ребро пирамиды.
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Выполняет построение призмы на плоскости по ее развертке и определяет ее вид.
|
1
|
Выполняет построение призмы
|
1
|
Определяет ее вид
|
1
|
Решает задачи на нахождение элементов призмы.
|
2
|
Выполняет построение чертежа к задаче
|
1
|
Использует формулу для нахождения диагонали параллелепипеда
|
1
|
Находит диагональ параллелепипеда
|
1
|
Применяет формулы площади боковой и полной поверхности призмы при решении задач
|
3
|
Выполняет построение чертежа к задаче
|
1
|
Находит площадь основания
|
1
|
Находит высоту призмы
|
1
|
Находит площадь боковой поверхности призмы
|
1
|
Находит площадь полной поверхности
|
1
|
Решает задачи на нахождение элементов пирамиды.
|
4
|
Выполняет построение чертежа к задаче
|
1
|
Определяет проекцию вершины на плоскости основания
|
1
|
Определяет и обосновывает прямоугольный треугольник
|
1
|
Применяет формулу соотношения в прямоугольном треугольнике
|
1
|
Вычисляет длину бокового ребра пирамиды
|
1
|
Итого:
|
15
|
Рубрика
для предоставления информации родителям по итогам суммативного оценивания
за раздел «Многогранники»
Фамилия обучающегося _________________________________________________
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Выполняет изображение призмы на плоскости
|
Затрудняется в изображении призмы на плоскости
|
Допускает ошибки в изображении призмы на плоскости
|
Выполняет изображение призмы на плоскости
|
Решает задачи на нахождение элементов призмы
|
Затрудняется в решении задачи на нахождение эле призмы
|
Допускает ошибки в решении задачи на нахождение элементов призмы
|
Решает задачи на нахождение элементов призмы
|
Применяет формулы площади боковой и полной поверхности призмы при решении задач
|
Затрудняется в применении формулы площади боковой и полной поверхности призмы при решении задач
|
Допускает ошибки в применении формулы площади боковой и полной поверхности призмы при решении задач
|
Применяет формулы площади боковой и полной поверхности призмы при решении задач
| |
|
|
 Скачать 223.65 Kb.
Скачать 223.65 Kb. 1. Постройте многогранник по его развертке и определите вид.
1. Постройте многогранник по его развертке и определите вид.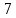 см и 9 см. Найдите диагональ параллелепипеда.
см и 9 см. Найдите диагональ параллелепипеда.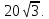 Боковое ребро наклонено к плоскости основания под углом 60°. Найди боковое ребро пирамиды.
Боковое ребро наклонено к плоскости основания под углом 60°. Найди боковое ребро пирамиды. 1. Постройте многогранник по его развертке и определите вид.
1. Постройте многогранник по его развертке и определите вид.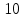 см,
см, 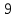 см и 8 см. Найдите диагональ параллелепипеда.
см и 8 см. Найдите диагональ параллелепипеда.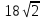 . Боковое ребро наклонено к плоскости основания под углом 45°. Найди боковое ребро пирамиды.
. Боковое ребро наклонено к плоскости основания под углом 45°. Найди боковое ребро пирамиды.