Проверка статистических гипотез. 5_Проверка статистических гипотез. Тема Проверка статистических гипотез 1 Основные понятия, используемые при проверке гипотез

• Название: Тема Проверка статистических гипотез 1 Основные понятия, используемые при проверке гипотез
• Анкор: Проверка статистических гипотез
• Дата: 25.05.2020
• Размер: 1.03 Mb.
• Имя файла: 5_Проверка статистических гипотез.doc
• Тип: Документы; #125212
• страница: 1 из 10

Тема 5. Проверка статистических гипотез

5.1 Основные понятия, используемые при проверке гипотез

5.1.1 Статистические гипотезы

Статистическая гипотеза – любое предположение, касающееся неизвестного распределения случайных величин (элементов), соответствующее некоторым представлениям об изучаемом явлении. В частном случае это может быть утверждение о значениях параметров распределения генеральной совокупности.

Различают нулевую и альтернативную гипотезы. Нулевая гипотеза – гипотеза, подлежащая проверке. Альтернативная гипотеза – каждая допустимая гипотеза, отличная от нулевой. Нулевую гипотезу обозначают Н₀, альтернативную – Н₁ (от Hypothesis – «гипотеза» (англ.)).

Конкретная задача проверки статистической гипотезы полностью описана, если заданы нулевая и альтернативная гипотезы. При обработке реальных данных большое значение имеет правильный выбор гипотез. Принимаемые предположения, например, нормальность распределения, должны быть тщательно обоснованы, в частности, статистическими методами. Необходимо помнить, что в подавляющем большинстве конкретных прикладных задач распределение результатов наблюдений в той или иной степени отлично от нормального.

5.1.2 Уровень значимости и мощность критерия. Ошибки при проверке гипотез

При проверке статистической гипотезы возможны ошибки. Есть два рода ошибок.

Ошибка первого рода заключается в том, что отвергают нулевую гипотезу, в то время как в действительности эта гипотеза верна. Вероятность ошибки первого рода называется уровнем значимости и обозначается α.

Ошибка второго рода состоит в том, что принимают нулевую гипотезу, в то время как в действительности эта гипотеза неверна.

Обычно используют не вероятность ошибки второго рода, а ее дополнение до 1. Эта величина носит название мощности критерия. Итак, мощность критерия – это вероятность того, что нулевая гипотеза будет отвергнута, когда альтернативная гипотеза верна.

Понятия уровня значимости и мощности критерия объединяются в понятии функции мощности критерия – функции, определяющей вероятность того, что нулевая гипотеза будет отвергнута.

Наглядным способом интерпретации ошибок является их графическое представление.

Предположим, что проверяется гипотеза Н0: о равенстве среднего значения генеральной совокупности заданной величине (известной, например, из предыдущих экспериментов).

Для этого берется выборка объема n, находится ее среднее арифметическое и по его величине судят о справедливости гипотезы Н0.

Распределение среднего арифметического при условии, что верна гипотеза Н0, будет . Это распределение качественно представлено на рис. 4.1.

Распределение среднего арифметического при условии, что верна альтернативная гипотеза Н1: , буде уже другим — .

Будем считать, что гипотеза Н0 отвергается, если выборочное среднее арифметическое окажется больше некоторого критического значения, т. е. , как показано на рис.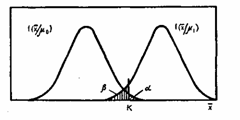



Рис. 6.1. Ошибки первого и второго рода

Область непринятия гипотезы Н0 называется критической областью критерия. Она показана па рисунке наклонной штриховкой. Уровень значимости будет соответствовать площади критической области.

Вероятность ошибки второго рода будет равна площади под кривой распределения , показанной на рисунке. вертикальной штриховкой.

Величина называется мощностью критерия.

Исследователь всегда должен формулировать гипотезу и задавать уровень значимости до получения экспериментальных данных, по которым эта гипотеза будет проверяться.

При выборе уровня значимости исследователь исходит из практических соображений, отвечая на вопрос: какую вероятность ошибки он считает допустимой для его конкретной задачи?

Обычно считают достаточным уровень значимости 0,05 (5%), иногда 1% или 10%, редко 0,1%.

5.1.3 Статистические критерии

Однозначно определенный способ проверки статистических гипотез называется статистическим критерием. Статистический критерий строится с помощью некоторой статистики U(x1, x2, …, xn) – функции от результатов наблюдений x1, x2, …, xn. В пространстве значений статистики U выделяют критическую область Ψ, т.е. область со следующим свойством: если значения применяемой статистики принадлежат данной области, то нулевую гипотезу отклоняют (иногда говорят – отвергают), в противном случае – не отклоняют (т.е. принимают).

Статистику U, используемую при построении определенного статистического критерия, называют статистикой этого критерия.
5.1.3 Общая схема проверки гипотез

Процедура проверки гипотез обычно проводится по следующей схеме:

1. 
   Формулируются гипотезы Н0 и Н1.
   
2. 
   Выбирается уровень значимости критерия.
   
3. 
   По выборочным данным вычисляется значение некоторой случайной величины, называемой статистикой критерия, или просто статистическим критерием, который имеет известное стандартное распределение (нормальное, Т-распределение Стьюдента и т.п.)
   
4. 
   Вычисляется критическая область и область принятия гипотезы. То есть находят критическое (граничное) значение критерия при выбранном уровне значимости.
   

5. Найденное значение критерия сравнивается с критическим и по результатам сравнения делается вывод: отвергнуть гипотезу или не отвергнуть. Если вычисленное по выборке значение критерия меньше чем критическое, то нулевую гипотезу Но не отвергают на заданном уровне значимости.

В этом случае наблюдаемое по экспериментальным данным различие генеральных совокупностей можно объяснить только случайностью выборки. Однако это совсем не означает доказательства равенства параметров генеральных совокупностей. Просто имеющийся в распоряжении статистический материал не дает оснований для отклонения гипотезы о том, что эти параметры одинаковы. Возможно, появится другой экспериментальный материал, на основании которого эта гипотеза будет отклонена.

Если вычисленное значение критерия больше критического, то гипотеза Н0 отклоняется в пользу гипотезы Н1 при данном уровне значимости.

В этом случае наблюдаемое различие генеральных совокупностей уже нельзя объяснить только случайностями и говорят, что наблюдаемое различие значимо (статистически значимо) на выбранном уровне значимости.

Следует подчеркнуть разницу между статистической значимостью и практической значимостью. Заключение о практической значимости всегда делается человеком, изучающим данное явление. И здесь истинным критерием является опыт и интуиция исследователя, а статистические критерии значимости — лишь формально точный инструмент, используемый в исследовании. Чем больше исследователь знает об изучаемом явлении, тем точнее будет сформулированная им гипотеза и тем точнее будут выводы, сделанные с помощью критериев значимости.

В настоящее время при проверке гипотез, особенно с использованием специализированных программных средств, уровень значимости до эксперимента точно не устанавливается, а по экспериментальным данным вычисляется вероятность Р того, что критерий (статистика критерия) выйдет за пределы значения, рассчитанного по выборке. Таким образом, Р — это экспериментальный (эмпирический уровень значимости. Точное значение Р обычно не указывают, а окончательные результаты приводят, сравнивая вычисленное значение критерия со стандартными значениями. Если, например, Р не превосходит 0,05, то на уровне значимости 5% различие считается статистически незначимым.

Критерии значимости подразделяются на три типа:

1. Критерии значимости, которые служат для проверки гипотез о параметрах распределений генеральной совокупности (чаще всего нормального распределения). Эти критерии называются параметрическими.

2. Критерии, которые для проверки гипотез не используют предположений о распределении генеральной совокупности. Эти критерии не требуют знания параметров распределений, поэтому называются непараметрическими.

3. Особую группу критериев составляют критерии согласия, служащие для проверки гипотез о согласии распределения генеральной совокупности, из которой получена выборка, с ранее принятой теоретической моделью (чаще всего нормальным распределением).

5.1.4 Односторонние и двусторонние критерии

Пусть цель исследования в том, чтобы выявить различие параметров двух генеральных совокупностей, которые соответствуют различным ее естественным условиям (условия жизни, возраст испытуемых и т. п.). Зачастую неизвестно, в какой из совокупностей рассматриваемый параметр будет больше, а какой меньше. Например, если сравнивают средние оценки учащихся в контрольной и экспериментальной группах, то заранее неизвестно, в какой группе средняя оценка будет больше. В этом случае нулевая гипотеза состоит в том, что средние равны между собой, а цель исследования — доказать обратное, т.е. наличие выявить различие между средними. При этом допускается, что различие может быть любого знака. Такие гипотезы называются двусторонними.

Но иногда задача состоит в том, чтобы доказать увеличение или уменьшение параметра; например, средний результат в экспериментальной группе выше (ниже), чем в контрольной. При этом уже не допускается, что различие может быть другого знака. Тогда альтернативная гипотеза при нулевой (или , если нулевая ). Такие гипотезы называются односторонними.

Критерии значимости, служащие для проверки двусторонних гипотез, называются двусторонними, а для односторонних гипотез — односторонними.

Выбор односторонней или двусторонней гипотезы находится за пределами формальных статистических методов и полностью зависит от целей исследования.

Например, необходимо доказать различие средних значений генеральных совокупностей (средних значений некоторого результата исследований) при двух различных методиках применяемых в контрольной и экспериментальной группах. Если неизвестно, какая группа покажет в среднем лучший результат, то нужно выдвинуть нулевую гипотезу против двусторонней альтернативы . Различие доказывается по разности средних арифметических результант в контрольной и экспериментальной группах ( ). Распределение разности при условии, что верна нулевая гипотеза Н0 схематично представлено на рис. 4.2, а.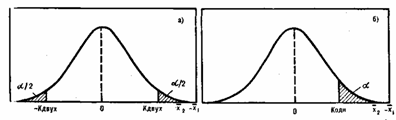

Рис. 6.2. Уровни значимости при двустороннем (а) и одностороннем (б) критериях

Решение об отклонении гипотезы Н0 принимается в том случае, если разность выходит за пределы некоторого значения двустороннего критерия (допустимы отклонения в обе стороны от нуля). Ошибка, которая при этом допускается, равна, как известно, уровню значимости . Но поскольку отклонения возможны в обе стороны, то при симметричном распределении вероятности отклонений, больших Кдвух и меньших Кдвух, будут одинаковы и составят /2.

Если предположить, что в экспериментальной группе будут показаны в среднем более высокие результаты, то можно выдвинуть одностороннюю альтернативу . В этом случае при той же нулевой гипотезе распределение разности будет таким же, как и для двустороннего критерия (см. рис. 4.2, б). Но теперь представляют интерес только положительные значения разности . Решение об отклонении Н0 принимается, когда окажется больше некоторого значения одностороннего критерия. При том же уровне значимости Кодн будет всегда меньше Кдвух, поэтому нулевая гипотеза будет при одностороннем критерии отклоняться чаще.

Таким образом, двусторонние критерии оказываются более консервативными, чем односторонние.

В этом нет никакого противоречия или доказательства несостоятельности статистических методов. Просто в первом случае, используя двустороннюю гипотезу, мы допускали и отрицательный эффект в экспериментальной группе. В такой ситуации выводы должны быть более осторожными, чем в случае односторонней гипотезы, когда имеется дополнительная информация, позволяющая сделать предположение о положительном эффекте новой программы, что, естественно, дает возможность сделать более точный вывод. Правда, следует отметить, что если превышение критического значения в каком либо исследовании незначительно, то в достоверности вывода о наличии положительного эффекта можно усомниться. В такой ситуации следует провести дополнительные исследования.

5.2 Проверка однородности выборок в прикладных задачах

В прикладных исследованиях часто возникает необходимость выяснить:

• 
  различаются ли генеральные совокупности, из которых взяты две независимые выборки;
  
• 
  изменилась ли генеральная совокупность после воздействия.
  

Например, надо выяснить, влияет ли способ упаковки молока на срок его хранения. Или: отличается ли потребительское поведение мужчин и женщин.

В маркетинге важно выделить сегменты потребительского рынка. Если установлена однородность двух выборок, то возможно объединение сегментов, из которых они взяты. В дальнейшем это позволит осуществлять по отношению к ним одинаковую маркетинговую политику (проводить одни и те же рекламные мероприятия и т.п.). Если же установлено различие, то поведение потребителей в двух сегментах различно, объединять эти сегменты нельзя, и могут понадобиться различные маркетинговые стратегии, своя для каждого из этих сегментов.

В математико-статистических терминах постановка задачи такова: имеются две выборки x1, x2,...,xm и y1, y2,...,yn, требуется проверить их однородность. Можно переформулировать задачу: требуется проверить, есть ли различие между выборками. Если имеющееся различие средних значений нельзя объяснить случайными статистическими колебаниями, то говорят о значимом различии.

5.2.1 Однородность выборок

Понятие «однородность», т. е. «отсутствие различия», может быть формализовано в терминах вероятностной модели различными способами:

А. Обе выборки взяты из одной генеральной совокупности, т. е. справедлива нулевая гипотеза

H₀ : F(x)=G(x) при всех х.

Отсутствие однородности означает, что верна альтернативная гипотеза, согласно которой

H₁ : F(x₀)G(x₀)

хотя бы при одном значении аргумента x₀. Если гипотеза H₀ принята, то выборки можно объединить в одну, если нет - то нельзя.

Б. В некоторых случаях целесообразно проверять не совпадение функций распределения, а совпадение некоторых характеристик случайных величин Х и Y - математических ожиданий, медиан, дисперсий, коэффициентов вариации и др. Например, однородность математических ожиданий означает, что справедлива гипотеза

H'₀ : M(X)=M(Y),

где M(Х) и M(Y) - математические ожидания случайных величин Х и Y, результаты наблюдений над которыми составляют первую и вторую выборки соответственно. Доказательство различия между выборками в рассматриваемом случае - это доказательство справедливости альтернативной гипотезы

H'₁ : M(X)  M(Y) .

Если гипотеза H0 верна, то и гипотеза H'0 верна, но из справедливости H'0 не следует обязательно справедливость H0: математические ожидания могут совпадать для различающихся между собой функций распределения. В частности, если в результате обработки выборочных данных принята гипотеза H'0, то отсюда не следует, что две выборки можно объединить в одну. Однако в ряде ситуаций целесообразна проверка именно гипотезы H'0 .

5.2.2 Независимость выборок

При сравнении двух (и более) выборок важным параметром является их зависимость. Если можно установить гомоморфную пару (то есть, когда одному случаю из выборки X соответствует один и только один случай из выборки Y и наоборот) для каждого случая в двух выборках (и это основание взаимосвязи является важным для измеряемого признака), такие выборки называются зависимыми. Примеры зависимых выборок: пары близнецов, два измерения какого-либо признака до и после экспериментального воздействия, мужья и жёны и т. п.

В случае, если такая взаимосвязь между выборками отсутствует, то эти выборки считаются независимыми, например: мужчины и женщины, психологи и математики.

Соответственно, зависимые выборки всегда имеют одинаковый объём, а объём независимых может отличаться.

Например, если проведено (т+п) измерений объемов продаж в (т+п) торговых точках, то описанную выше модель, как правило, можно применять. Если же, например, x_i и y_i- объемы продаж одного и того же товара до и после определенного рекламного воздействия, то используют модель связанных (зависимых) выборок.

5.2.3 Параметрические и непараметрические гипотезы

В зависимости от формулировки статистических гипотез различают параметрические и непараметрические статистические гипотезы.

Предположение, которое касается неизвестного значения параметра распределения, входящего в некоторое параметрическое семейство распределений, называется параметрической гипотезой (напомним, что параметр может быть и многомерным).

Большинство параметрических методов разработаны для нормально распределенных совокупностей. Некоторые методы позволяют анализировать данные, распределенные по другим законам (например, биномиальному или Пуассона).

Предположение, при котором вид распределения не рассматривается (т.е. не предполагается, что оно входит в некоторое параметрическое семейство распределений), называется непараметрической гипотезой.

Непараметрические методы позволяют исследовать данные без допущений о характере распределения переменных. Так как в этих тестах обрабатывается не само измеренное значение, а его ранг, то эти тесты нечувствительны к выбросам. Непараметрические тесты могут применяться в тех случаях, когда переменные измерены при помощи порядковой или метрической шкалы. Существуют тесты, предназначенные для анализа номинальных данных.

Непараметрические методы наиболее приемлемы, когда объем выборок мал. Если данных много (например, n>100), то не имеет смысла использовать непараметрические статистики. Когда выборки становятся очень большими, то выборочные средние подчиняются нормальному закону, даже если исходная переменная не является нормальной или измерена с погрешностью. Таким образом, параметрические методы, являющиеся более чувствительными (имеют большую статистическую мощность), практически всегда подходят для больших выборок.