Проверка статистических гипотез. 5_Проверка статистических гипотез. Тема Проверка статистических гипотез 1 Основные понятия, используемые при проверке гипотез
 Скачать 1.03 Mb.
|
|
5.6.2 Сравнение двух зависимых выборок с использованием теста Уилкоксона (Вилкоксона) Тест известен также как знаковый ранговый критерий Уилкоксона, критерий знаковых рангов Уилкоксона, одновыборочный критерий Вилкоксона. Критерий применяется для сопоставления двух зависимых выборках. С его помощью можно определить, является ли сдвиг показателя в каком-то одном направлении более существенным, чем в другом. Нулевая гипотеза H0={существенность сдвигов в типичном направлении не превосходит существенности сдвигов в нетипичном направлении}. На объём выборки накладывается условие: 5≤n≤50. Алгоритм проверки: Вычисляются разности между индивидуальными значениями показателя после проведения эксперимента и до него. Модули разностей ранжируются в порядке возрастания. Отмечаются ранги, соответствующие сдвигам в нетипичном направлении. Например, если в большинстве случаев после проведения эксперимента наблюдалось увеличение измеряемого параметра, то его уменьшение следует считать нетипичным сдвигом. Эмпирическое значение критерия определяется как сумма рангов, соответствующих нетипичным сдвигам. Если критическое значение не превосходит эмпирического, то на данном уровне значимости отсутствуют основания для отклонения нулевой гипотезы о несущественности различий. В противном случае нулевая гипотеза отвергается. Таким образом, схема применения критерия Вилкоксона будет иметь следующий вид: 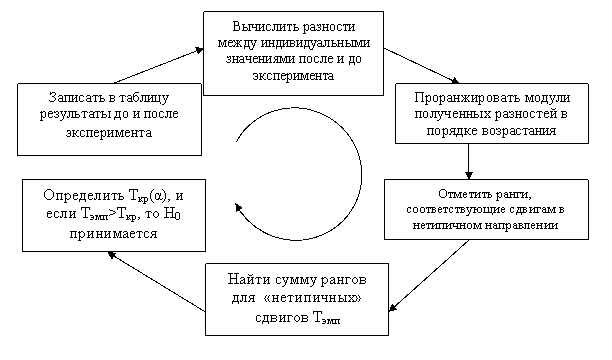 Критерий Вилкоксона позволяет установить не только направленность изменений, но и их выраженность. Следующий рассматриваемый нами критерий служит только для определения направления изменения в двух связанных выборках. Этот тест предъявляет к исследуемой выборке следующие требования: шкала измерений должна быть порядковой, интервальной или относительной (т.е. тест нельзя применять к номинальным переменным). исследуемое распределение должно быть непрерывно и симметрично относительно своей медианы число различных значений в массиве X должно быть не менее 5 Предположение о симметричности распределения является критичным для работы теста. В случае, если оно не выполняется, тест неприменим и возвращаемые им уровни достоверности некорректны. В этом случае можно использовать менее мощный, но более общий критерий знаков. Пример сравнения двух зависимых выборок с использованием теста Уилкоксона (Вилкоксона) Для демонстрации применения критерия определим значимость различий изменений вербальной памяти до и после иппотерапии (в баллах), используя следующие данные:
В рассмотренном примере имеется только один такой сдвиг (см. таблицу), которому соответствует ранг, равный 5. Поэтому эмпирическое значение критерия будет численно равно этому рангу:  . Критическое значение на уровне значимости 5%  (приложение 6).Так как  , то нулевую гипотезу следует отвергнуть и считать различия существенными.5.7 Сравнение нескольких выборок Для сравнения нескольких выборок используется: дисперсионный анализ для случая нормально распределенных переменных с однородными дисперсиями; непараметрические критерии – для распределений, отличных от нормальных и для малых выборок. Для сравнения более чем двух независимых выборок по уровню выраженности переменных применяется несколько критериев: Н-критерий Крускала (Краскала(-Уоллеса (Уоллиса), критерий медиан, критерий Джонкира-Терспта. Из них наибольшей чувствительностью к различиям обладает критерий Крускала-Уоллиса. Этот критерий является непараметрическим аналогом дисперсионного анализа. Отличия состоят в том, что: сравниваются не средние значения переменных, а средние значения их рангов; используется не F-критерий Фишера, а критерий хи-квадрат. Дисперсионный анализ обеспечивает более точные результаты, но условием его применения является нормальное распределение значений признака и однородность дисперсий или достаточно большой размер выборок. Для малых выборок и распределений, отличающихся от нормальных рекомендуется использовать критерий Крускала-Уоллиса. 5.7.1 Сравнение нескольких независимых выборок. Критерий Крускала-Уоллиса Критерий Краскела — Уоллиса предназначен для проверки равенства медиан нескольких выборок. Он является обобщением U-критерия Манна-Уитни на случай  несвязанных выборок ( ) и предназначен для оценки различий по уровню какого-либо признака одновременно между тремя и более выборками.Критерий Краскела — Уоллиса является ранговым, поэтому он инвариантен по отношению к любому монотонному преобразованию шкалы измерения. Нулевая гипотеза H0={между выборками существует лишь случайные различия по уровню исследуемого признака}. Альтернативная гипотеза Н1={между выборками имеются существенные различия}. Значения признака ранжируются для всех выборок, как для одной, в порядке возрастания. Далее рассчитывают суммы рангов для каждой выборки отдельно. Выборки могут быть как разных, так и равных объемов. Эмпирическое значение критерия Крускала-Уоллиса рассчитывается по следующей формуле:  ,где  – общее количество испытуемых,  – сумма рангов в  -ой выборке,  – число испытуемых в -ой выборке.Нулевая гипотеза сдвига отклоняется на уровне значимости  , если  , где  — критическое значение, вычисляемое при  (количество выборок) и  по специальным таблицам. При бо́льших значениях применимы различные аппроксимации, например, при  справедлива аппроксимация распределения статистики распределением  со степенями свободы  , то есть нулевая гипотеза отклоняется, если  .Схема применения критерия Крускала-Уоллиса выглядит следующим образом 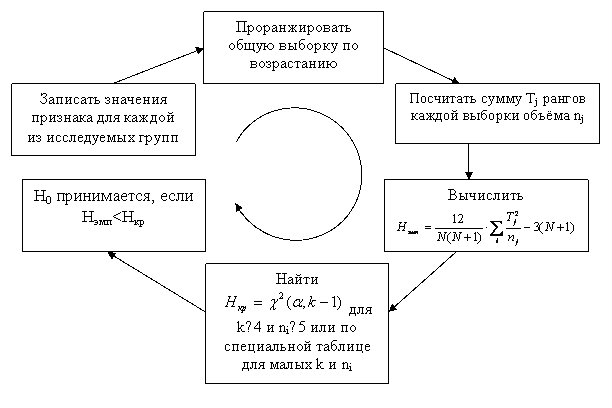 Рис 1 Алгоритм применения критерия Крускала-Уоллиса Пример использования критерия Крускала-Уоллиса Одинакова ли степень освоения нового материала младших и старших школьников и учителей. Таблица 1
Значения признака ранжируется для всех выборок, как для одной, в порядке возрастания. Далее вычисляются суммы рангов для каждой выборки отдельно (т.е. произведём суммирование рангов по строкам, см. таблицу). Таблица 2
Эмпирическое значение критерия:  В рассматриваемом примере количество испытуемых во всех группах одинаково и равно 9. На практике выборки могут быть разных объёмов. Критическое значение критерия по уровню значимости и степени свободы . При этом степень свободы рассчитывается как разность количества групп и единицы, то есть  . При  критическое значение  . В данном случае нулевая гипотеза на уровне значимости 0.05 не отвергается, выборки не имеют существенных отличий по исследуемому признаку.5.7.2 Сравнение нескольких зависимых выборок. Критерий Фридмана Критерий Фридмана является непараметрическим аналогом однофакторного дисперсионного анализа для повторных измерений. Он позволяет проверять гипотезы о различии более чем двух повторных измерений по уровню выраженности изучаемой переменной. Критерий более эффективен, чем дисперсионный анализ в случае малых выборок и распределений, отличных от нормального. Он основан на ранжировании повторных измерений для каждого объекта выборки. Проверяется при помощи критерия . Критерий применяется для сопоставления показателей, измеренных в разных условиях ( ) на одной и той же выборке из  испытуемых. Критерий Фридмана позволяет установить, что величины показателей от условия к условию изменяются, но при этом не указывает на направление изменений и в этом смысле он похож на критерий знаков.Критерий Фридмана является обобщением критерия Вилкоксона на большее, чем два, количество условий измерения, при этом ранжируются не абсолютные величины сдвигов, а сами индивидуальные значения измерений. Нулевая гипотеза H0={между полученными в разных условиях показателями существуют лишь случайные различия}. Альтернативная гипотеза H1={между полученными в разных условиях показателями имеются существенные различия}. Ранжируются индивидуальные значения показателей (повторные измерения) для каждого экземпляра выборки в порядке убывания признака (ранжирование параметров каждой строки). Полученные ранги суммируются по столбцам (ранги показателей, полученных по всем экземплярам выборки при одних и тех же условиям). Эмпирическое значение критерия по формуле:  ,где  – количество условий (тестов),  , – количество экземпляров выборки,  ,  – сумма рангов всех значений  при -ом условии.Критическое значение критерия  зависит от уровня значимости α и степени свободы  .Нулевая гипотеза не отвергается, если критическое значение превосходит эмпирическое. В этом случае различия значений показателя в разных условиях можно считать несущественными. Схема применения критерия имеет вид: 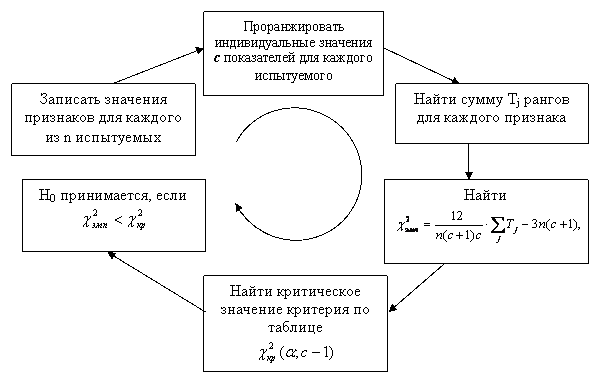 Рис 2 Алгоритм применения критерия Фридмана Пример использования критерия Фридмана Пять учащихся исследуются по четырём тестам. Являются ли результаты тестирования случайными? Таблица 3
Проранжируем индивидуальные значения показателей для каждого испытуемого в порядке убывания признака. Т.е. производим ранжирование параметров каждой строки представленной таблицы. Найдём суммы рангов по столбцам. В результате получаем: Таблица 4
Эмпирическое значение критерия:  Критическое значение критерия , зависит от уровня значимости α и степени свободы . Для  и критическое значение  . Нулевая гипотеза не отвергается, так как критическое значение превосходит эмпирическое.  .5.8 Использование критерия согласия Пирсона Критерий согласия -Пирсона позволяет осуществлять проверку эмпирического и теоретического (либо другого эмпирического) распределений одного признака. Данный критерий применяется, в основном, в двух случаях:для сопоставления эмпирического распределения признака с теоретическим распределением (нормальным, показательным, равномерным либо каким-то иным законом); для сопоставления двух эмпирических распределений одного и того же признака. Идея метода – определение степени расхождения соответствующих частот 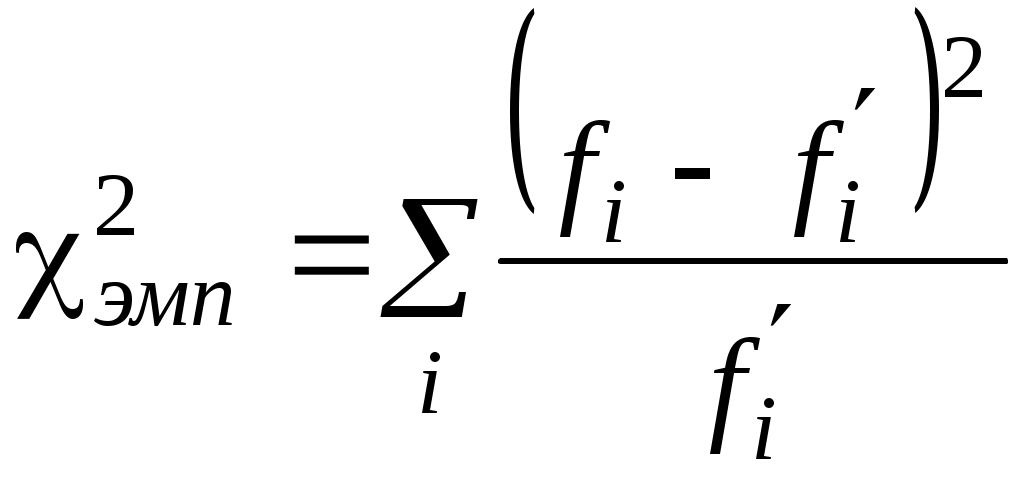 и  ; чем больше это расхождение, тем больше значение  : Объемы выборок должны быть не меньше 50 и необходимо равенство сумм частот  .Нулевая гипотеза H0={два распределения практически не различаются между собой}; альтернативная гипотеза – H1={расхождение между распределениями существенно}. Приведем схему применения 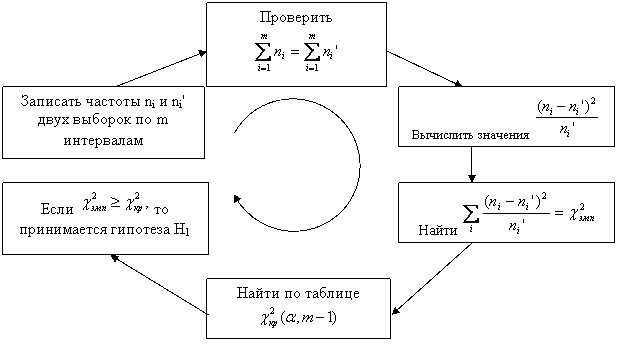-критерия для сопоставления двух эмпирических распределений: Пример использования критерия Пирсона Среди школьников с 1 по 7 класс в течение двух недель проводился опрос об удовлетворенности собственными оценками. Результаты опроса представлены в таблице: Таблица
Можно ли считать, что эмпирическое распределение на первой неделе исследования согласуется с эмпирическим распределением на второй неделе исследования, т.е. структура удовлетворенности ответами учащихся сохранилась в течение данного времени? Вычислим эмпирическое значение критерия: 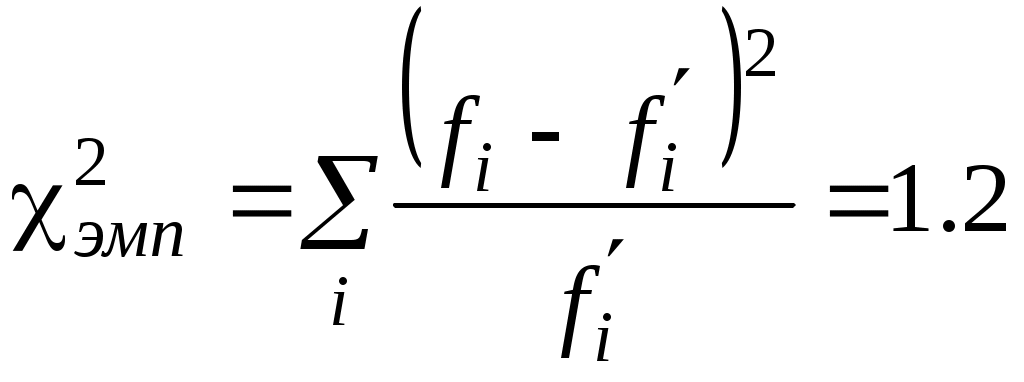 По таблице критических точек распределения по принятому уровню значимости 0,05 и числу степеней свободы k=7-1 находим критическую точку  .Поскольку  , то нет оснований отвергать нулевую гипотезу об одинаковом распределении мнений учащихся о своей успеваемости в разные недели.5.9 Проверка статистических гипотез применительно к таблицам сопряженности Таблица сопряженности - средство представления совместного распределения двух переменных, предназначенное для исследования связи между ними. Таблица сопряженности является наиболее универсальным средством изучения статистических связей, так как в ней могут быть представлены переменные с любым уровнем измерения. Строки таблицы сопряженности соответствуют значениям одной переменной, столбцы - значениям другой переменной (количественные шкалы предварительно должны быть сгруппированы в интервалы). На пересечении строки и столбца указывается частота совместного появления соответствующих значений двух признаков  и  . Сумма частот по строке  называется маргинальной частотой строки; сумма частот по столбцу  - маргинальной частотой столбца. Сумма маргинальных частот равна объему выборки ; их распределение представляет собой одномерное распределение переменной, образующей строки или столбцы таблицы. В таблицах сопряженности могут быть представлены как абсолютные, так и относительные частоты (в долях или процентах). Относительные частоты могут рассчитываться по отношению: к маргинальной частоте по строке к маргинальной частоте по столбцу к объему выборки Таблицы сопряженности используются для проверки гипотезы о наличии связи между двумя признаками, а также для измерения тесноты связи. Для анализа таблиц сопряженности при проверке гипотезы о наличии связи между двумя признаками может быть использован критерий "хи-квадрат". Гипотеза H0: переменные  и  независимы.Пусть имеется таблица сопряженности  , построенная для переменных и :
Введем следующие обозначения:  - наблюдаемая частота для соответствующей ячейки; - ожидаемая частота в случае правильности нулевой гипотезы.Тогда статистика "хи-квадрат" может быть рассчитана по формуле: 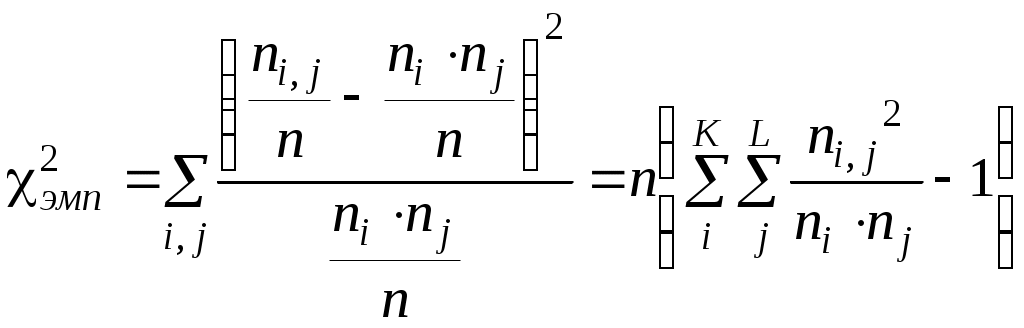 Условия применимости:  ; не более чем в 20% ячеек n>40.Эмпирическое значение критерия сравнивается с критическим  . Если эмпирическое значение критерия не больше критического, то нулевая гипотеза не отвергается и переменные и на выбранном уровне значимости могут считаться независимыми. Для частного случая  таблица сопряженности принимает вид:
Статистика рассчитывается по упрощенной формуле:  Пример применения критерия  Эффективны ли занятия на подготовительных курсах (ПК) при поступлении на факультет информатики и управления (ИФ). Данные о поступивших на факультет ИФ ХПИ представлены в таблице:
Нулевая гипотеза H0: ПК не эффективны. В данном случае , следовательно, можно применить упрощенную формулу:  Критическое значение критерия  , следовательно ,Гипотеза H0 отвергается, т.е. ПК эффективны для поступления на НТУ «ХПИ». Критерий Мак-Немара Критерий Мак-Нимара (также, К. Мак-Немара, англ. McNemar's test) используется для анализа таблиц сопряженности размером 2x2 (для дихотомического признака). В отличие от критерия хи-квадрат, критерий Мак-Немара применяется, когда условие независимости наблюдений не просто не выполняется, но, напротив, учет признака выполняется на одних и тех же субъектах. Этот тест проводится в следующих случаях: для одной и той же выборки определяются значения двух дихотомических переменных (например, любовь к сладкому и предпочтение чая или кофе); для одной и той же выборки определяется значение одной дихотомической переменной до воздействия и после воздействия (например, отношение к товару до и после просмотра рекламы). Пусть дихотомическая переменная принимает значения  и  , а дихотомическая переменная принимает значения  и  .
Нулевая гипотеза утверждает, что маргинальные распределения для всех исходов совпадают: Расчет эмпирического значения критерия  производится (для b≠c) следующим образом:а) если b+c=q≤20, то находится по таблице M(n,m), где m=min(b,c).б) если b+c>20, то вычисляется по формуле При b=c рекомендуется использовать -критерий. Определение критического значения зависит от способа определения эмпирического значения. Алгоритм применения критерия Макнамары можно описать следующей схемой: 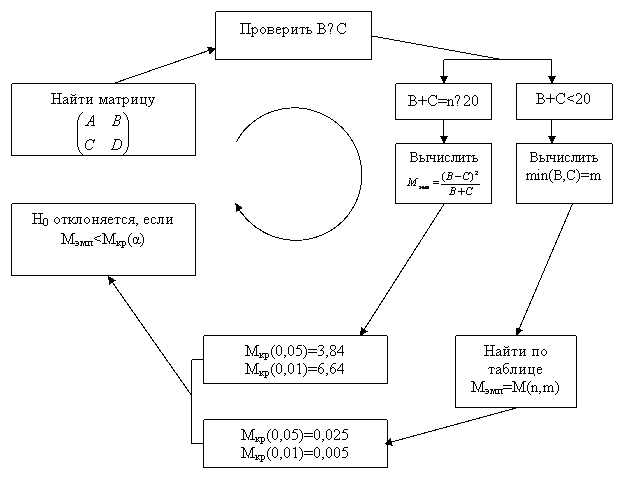 Для повышения качества критерия на выборках с низкочастотными событиями применяют скорректированную формулу Йейтса:  или скорректированную формулу Эдвардса:  Пример применения критерия Мак-Немара Учащиеся тестировались до и после проведения тренинга по повышению качества усвоения учебного материала Экспериментальные данные, представляют итог прохождения теста: «+» – тест пройден успешно; «–« – тест не пройден. Результаты представлены в четырехпольной таблице.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
