5_Проверка статистических гипотез. Тема Проверка статистических гипотез 1 Основные понятия, используемые при проверке гипотез

• Название: Тема Проверка статистических гипотез 1 Основные понятия, используемые при проверке гипотез
• Анкор: 5_Проверка статистических гипотез.doc
• Дата: 29.01.2017
• Размер: 1.03 Mb.
• Имя файла: 5_Проверка статистических гипотез.doc
• Тип: Документы; #1139
• страница: 2 из 10

5.3 Параметрические методы проверки однородности выборок

5.3.1 Традиционный метод проверки однородности двух независимых выборок (критерий Стьюдента)

Наиболее распространенный метод проверки однородности выборок путем выдвижения и проверки параметрических гипотез основан на применении критерия Стьюдента.

Рассмотрим случай сравнения двух независимых выборок.

Выдвигаются: нулевая гипотеза о равенстве средних и альтернативная, о том, что средние не равны.

Вычисляют выборочные средние арифметические и дисперсии в каждой выборке и статистику Стьюдента t, на основе которой принимают решение.

По заданному уровню значимости  и числу степеней свободы (m+n-2) из таблиц распределения Стьюдента находят критическое значение t_кр. Если |t|>t_кр, то гипотезу однородности (отсутствия различия) отклоняют, если же |t|<t_кр, то принимают.

В приложении 1 приведены основные формулы и условия применения традиционного метода проверки равенства математических ожиданий, дисперсий, а также долей успешных исходов экспериментов в двух совокупностях

5.3.2 Классические условия применимости критерия Стьюдента

Согласно математико-статистической теории должны быть выполнены два условия применимости критерия Стьюдента, основанного на использовании статистики t, заданной формулой (1):

• 
  а) результаты наблюдений имеют нормальные распределения:
  
• 
  F(x)=N(x; m₁, ₁²), G(x)=N(x; m₂, ₂²)
  

с математическими ожиданиями m₁ и m₂ и дисперсиями ₁² и ₂² в первой и во второй выборках соответственно;

• 
  б) дисперсии результатов наблюдений в первой и второй выборках совпадают:
  

D(X)=₁²=D(Y)=₂².

Если условия а) и б) выполнены, то нормальные распределения F(x) и G(x) отличаются только математическими ожиданиями, а поэтому обе гипотезы H₀ и H'₀ сводятся к гипотезе

H"₀ : m₁=m₂, ,

а обе альтернативные гипотезы H₁ и H'₁ сводятся к гипотезе

H"₁ : m₁m₂, .

Если условия а) и б) выполнены, то статистика t при справедливости H"0 имеет распределение Стьюдента с (n+m-2) степенями свободы. Только в этом случае описанный выше традиционный метод обоснован безупречно. Если хотя бы одно из условий не выполнено, то нет никаких оснований считать, что статистика t имеет распределение Стьюдента, поэтому применение традиционного метода, строго говоря, не обосновано.

В большинстве случаев априори нет оснований предполагать нормальность распределения результатов экономических, технико-экономических, технических, медицинских и иных наблюдений.

Однако проверка нормальности - более сложная и трудоемкая статистическая процедура, чем проверка однородности, требующая большого числа наблюдений.

Тем не менее, несмотря на нарушение условия нормальности традиционный метод (критерий Стьюдента) можно использовать для проверки гипотезы о равенстве мат. ожиданий при больших объемах выборок. При этом вместо таблиц распределения Стьюдента достаточно пользоваться таблицами стандартного нормального распределения Ф(х).

Иногда условие равенства дисперсий вытекает из методики получения результатов наблюдений, например, когда с помощью одного и того же прибора или методики m раз измеряют характеристику первого объекта и п раз - второго, а параметры распределения погрешностей измерения при этом не меняются. Однако, в большинстве технических, экономических, медицинских и иных задач условие равенства дисперсий нельзя считать выполненным, а проверять его нецелесообразно.

Однако при больших и равных или мало различающихся объемах выборок нет необходимости требовать выполнения условия равенства дисперсий.

В таких случаях применение t-критерия позволяет проверять гипотезу H'₀ о равенстве математических ожиданий, но не гипотезу H₀о том, что обе выборки взяты из одной и той же генеральной совокупности. Классические условия применимости критерия Стьюдента в подавляющем большинстве технических, экономических, медицинских и иных задач не выполнимы. Тем не менее, при больших и примерно равных объемах выборок его можно применять. При конечных объемах выборок традиционный метод носит неустранимо приближенный характер.

Кроме того, следует обратить внимание на то, что t-критерий можно использовать лишь при выполнении следующих условий:

1. Наблюдения в каждой из рассматриваемых групп взяты случайным образом из одной и той же генеральной совокупности (например, две группы студентов одного курса или дети одного возраста и т.д.)

2. Наблюдения имеют нормальные распределения или объем каждой выборки превышает 30 значений.

5.3.3 Использование критерия Крамера-Уэлча при проверке равенства математических ожиданий двух независимых выборок

Вместо критерия Стьюдента для проверки равенства мат. ожиданий целесообразно использовать критерий Крамера-Уэлча, который в отличие от критерия Стьюдента не требует для своего использования равенства дисперсий D(X)=D(Y). Применение критерия Крамера-Уэлча основано на статистике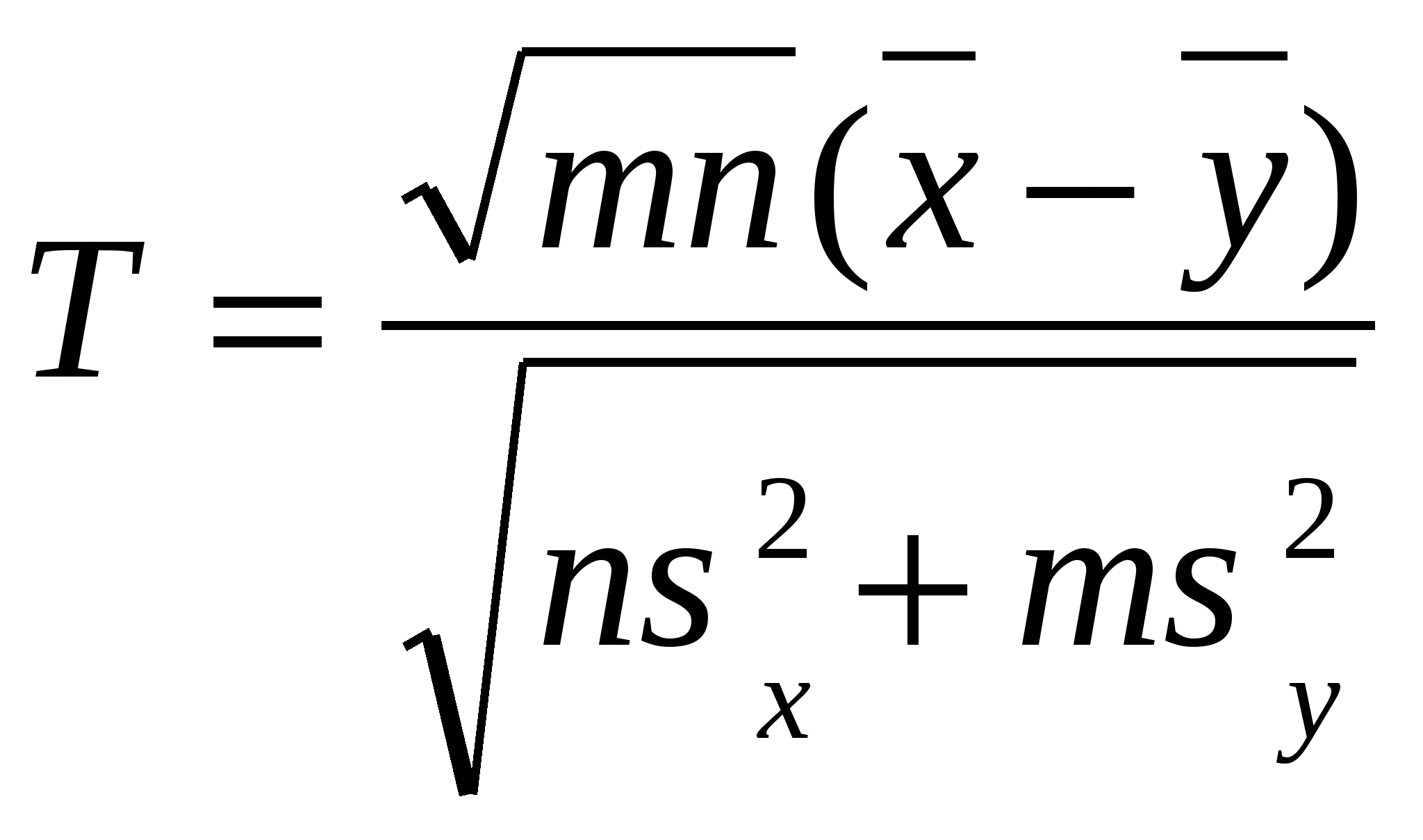

.

Правило принятия решения для критерия Крамера-Уэлча выглядит так:

• 
  если |T|<то гипотеза однородности (равенства) математических ожиданий принимается на уровне значимости
  
• 
  если же |T|>то гипотеза однородности (равенства) математических ожиданий отклоняется на уровне значимости .
  

Эмпирическое значение критерия Крамера-Уэлча есть приближенное значение эмпирического значения t-критерия Стьюдента. В прикладной статистике наиболее часто применяется уровень значимости Тогда значение модуля статистики Т Крамера-Уэлча надо сравнивать с граничным значением

5.3.4 Сравнение среднего с нормативом (t-тест одной выборки)

Этот тест позволяет выяснить, отличается ли среднее значение, полученное на основе данной выборки, от предварительно заданного контрольного значения.

Выдвигаются гипотезы

Вычисляется значение статистики t по формуле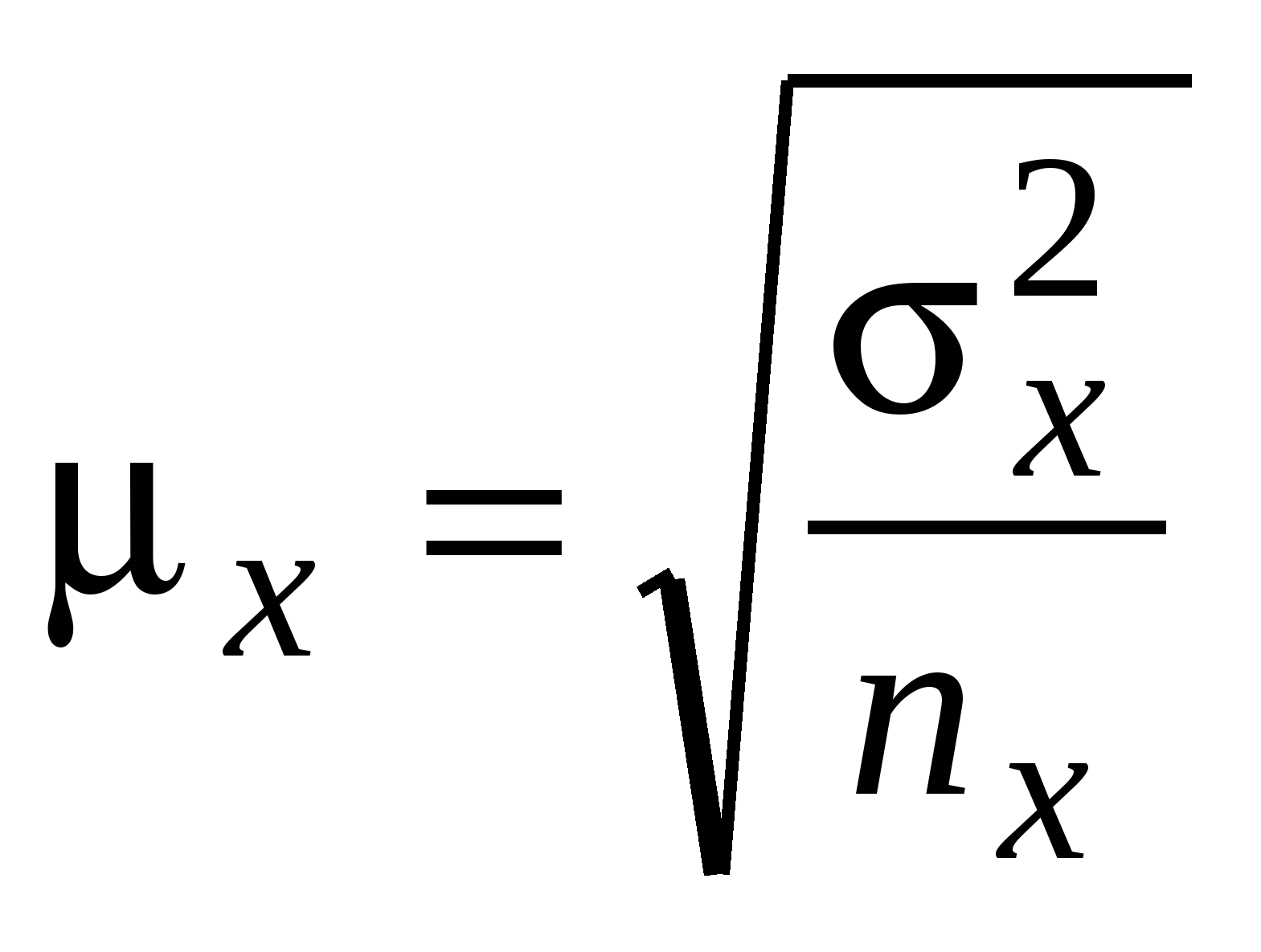

, где

Значимость отличия среднего от заданного значения определяется на основании сравнения полученной статистики t с критической или в зависимости от полученной величины наблюдаемого уровня значимости. Если наблюдаемый уровень значимости меньше необходимого (например, 0,05), то считается, что среднее значение существенно отличается от нормативной величины.

5.3.5 Сравнение двух зависимых выборок при помощи t-критерия Стьюдента

Цель: определить, есть ли достоверные статистические различия между средними значениями генеральных совокупностей, из которых сформированы две исследуемые зависимые выборки.

Нулевая гипотеза: между средними значениями генеральных совокупностей, из которых сформированы две исследуемые зависимые выборки отсутствуют достоверные статистические различия (M1=M2)

Альтернативная гипотеза: между средними значениями генеральных совокупностей, из которых сформированы две исследуемые зависимые выборки есть достоверные статистические различия. Среднее значение первой выборки достоверно выше среднего значения второй выборки или среднее значение второй выборки достоверно выше среднего значения первой выборки.

Ограничения метода:

1. 
   Каждое значение одной переменной, логически сопоставлено со значением другой переменной (признак измерен на одной и той же выборке дважды, выборки имеют одинаковый размер);
   
2. 
   Данные двух выборок положительно коррелируют между собой;
   
3. 
   Измеренные данные в выборках подчиняются закону нормального распределения или имеют достаточно большой объем (если требование не выполняется, в качестве альтернативы используют непараметрический T-критерий Вилкоксона).
   

,

где – средняя разность значений; – стандартное отклонение разностей, - размер выборки, число степеней свободы . Для определения уровня значимости используется таблица критических значений -критерия Стьюдента. В случае если эмпирическое≥критическое, то нулевая гипотеза о равенстве средних отклоняется на выбранном уровне статистической значимости.

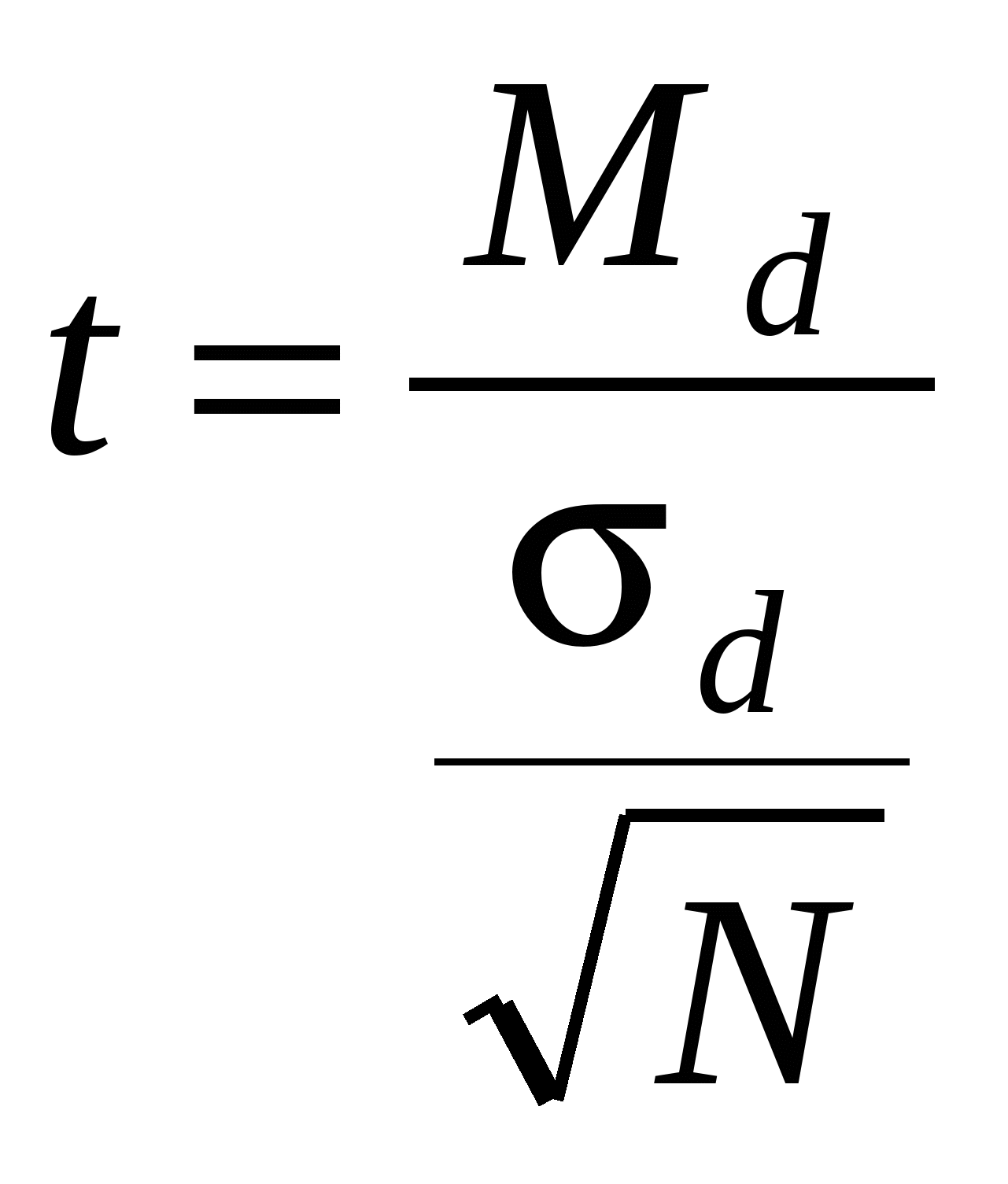5.4 Непараметрические методы проверки однородности выборок

Критерии сравнения, которые могут быть применены как количественным, так и к порядковым совокупностям, называются непараметрическими. Использование этих критериев не нуждается в каких-либо предположениях о характере распределения переменных. Так как их применение не требует оценки параметров распределений, то критерии называют непараметрическими (термин ввел Вольфовиц в 1942 г.), или - свободными от параметров, или свободно распределенными

Непараметрические критерии обладают рядом преимуществ:

• 
  они не требуют предварительных предположений относительно вида исходного распределения;
  
• 
  для их вычисления не требуется большого объема данных;
  
• 
  они являются более робастными (применимыми в широком диапазоне условий), чем их параметрические аналоги.
  

Недостатки непараметрических критериев:

• 
  низкая статистическая мощность (менее чувствительные);
  
• 
  меньшая гибкость;
  
• 
  большая вероятность совершить ошибку II рода - отклонить нулевую гипотезу, когда она верна.
  

5.5 Сравнение двух независимых выборок

5.5.1 Сравнение двух независимых выборок Критерий Манна–Уитни

Наиболее часто для сравнения двух независимых выборок используется U-критерий Манна–Уитни –– статистический критерий, используемый для оценки различий между двумя независимыми выборками по уровню какого-либо признака, измеренного количественно.

В отличие от t-критерия Стьюдента U-критерий не требует проверки на нормальность распределения, с его помощью можно сравнивать маленькие выборки объёмом от 3-х наблюдений, т.е. тест позволяет выявлять различия в значении параметра между малыми выборками.

Данный метод выявления различий между выборками был предложен в 1945 году Фрэнком Уилкоксоном (F. Wilcoxon). В 1947 году он был существенно переработан и расширен Х. Б. Манном (H. B. Mann) и Д. Р. Уитни (D. R. Whitney), по именам которых сегодня обычно и называется.

Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны. Иногда эти различия называют различиями в расположении двух выборок.

Для корректной работы теста требуется выполнение следующих условий:

• 
  распределения X и Y непрерывны (или являются дискретными распределениями, хорошо аппроксимирующими непрерывное распределение);
  
• 
  распределения X и Y имеют одинаковую форму, единственным возможным отличием является их расположение (т.е. медиана);
  
• 
  выборки независимы;
  
• 
  тест нельзя применять к номинальным переменным;
  
• 
  в каждой выборке должно быть не менее 3 наблюдений: n1,n2 ≥ З; допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5;
  
• 
  в выборочных данных не должно быть совпадающих значений (все числа — разные) или таких совпадений должно быть достаточно мало.
  

Первым рядом (выборкой, группой) выбирается тот ряд значений, в котором значения, по предварительной оценке, выше, а вторым рядом - тот, где они предположительно ниже.

Гипотезы U - критерия Манна-Уитни:

H₀: Уровень признака в группе 2 не ниже уровня признака в группе 1.

H₁: Уровень признака в группе 2 ниже уровня признака в группе 1.

Для применения U-критерия Манна — Уитни нужно произвести следующие операции:

1. 
   Составить единый ранжированный ряд из обеих сопоставляемых выборок, расставив их элементы по степени нарастания признака и приписав меньшему значению меньший ранг. Общее количество рангов получится равным: , где — количество единиц в первой выборке, а — количество единиц во второй выборке.
   
2. 
   Если имеются одинаковые значения, им присваивается средний ранг.
   
3. 
   Подсчитать отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно — на долю элементов второй выборки.
   
4. 
   Определить большую из двух ранговых сумм (), соответствующую выборке с единиц.
   
5. 
   Определить значение U-критерия Манна — Уитни по формуле:
   

6. 
   По таблице для избранного уровня статистической значимости определить критическое значение критерия для данных и . Если полученное значение U меньше табличного или равно ему, то признается наличие существенного различия между уровнем признака в рассматриваемых выборках (отвергается нулевая гипотеза). Если же полученное значение U больше табличного, то нулевая гипотеза не отвергается. Достоверность различий тем выше, чем меньше значение U.
   

Пример проверки гипотезы при помощи U-критерия Манна-Уитни

Проверим гипотезу о принадлежности сравниваемых независимых выборок к одной и той же генеральной совокупности с помощью непараметрического U-критерия Манна-Уитни. Для расчета U-критерия расположим значения сравниваемых выборок в порядке возрастания в один обобщенный ряд и присвоим вариантам обобщенного ряда ранги от 1 до . Первая строка представляет собой значения первой выборки, вторая - второй выборки, третья - соответствующие ранги в обобщенном ряду:

6	7	7	8	8		9	9	9			10	11
					8				9	9			11	11	12	12	12	13	13
1	2,5	2,5	5	5	5	9	9	9	9	9	12	14	14	14	17	17	17	19,5	19,5

Если имеются одинаковые варианты, им присваивается средний ранг, однако значение последнего ранга должно быть равно (в нашем случае 20). Это правило используют для проверки правильности ранжирования. Отдельно для каждой выборки рассчитываем суммы рангов их рангов и . В нашем случае:





Для проверки правильности вычислений можно воспользоваться правилом:



В рассматриваемом случае .

Статистика

Для проверки одностороннего критерия определим критическое значение для и уровня значимости 5%, которое равно (таблица критических значений критерия приведены в приложении 2). Так как вычисленное значение критерия меньше табличного, нулевая гипотеза отвергается на выбранном уровне значимости, и различия между выборками признаются статистически значимыми. Таким образом, вывод о существовании различий подтверждается с помощью данного непараметрического теста.