5_Проверка статистических гипотез. Тема Проверка статистических гипотез 1 Основные понятия, используемые при проверке гипотез
 Скачать 1.03 Mb.
|
|
5.5.2 Сравнение двух независимых выборок. Критерий серий Вальда—Вольфовица Критерий серий Вальда—Вольфовица представляет собой непараметрическую альтернативу  -критерию для независимых выборок. Данные имеют тот же вид, что и в -критерии для независимых выборок. Файл должен содержать группирующую (независимую) переменную, принимающую, по крайней мере, два различных значения (кода), чтобы однозначно определить, к какой группе относится каждое наблюдение. Критерий серий Вальда—Вольфовица устроен следующим образом. Представьте, что вы хотите сравнить мужчин и женщин по некоторому признаку. Вы можете упорядочить данные, например, по возрастанию, и найти те случаи, когда субъекты одного и того же пола примыкают друг к другу в построенном вариационном ряде (иными словами, образуют серию). Если нет различия между мужчинами и женщинами, то число и длина «серий», относящиеся к одному и тому же полу, будут более или менее случайными. В противном случае две группы (мужчины и женщины) отличаются друг от друга, то есть не являются однородными. Критерий предполагает, что рассматриваемые переменные являются непрерывными и измерены, по крайней мере, в порядковой шкале. Критерий серий Вальда—Вольфовица проверяет гипотезу о том, что две независимые выборки извлечены из двух популяций, которые в чем-то существенно различаются между собой, иными словами, различаются не только средними, но также формой распределения. Серийный критерий позволяет обнаружить различие между двумя выборками не только по центральной тенденции, но и по другим характеристикам. Нулевая гипотеза заключается в предположении, что ряды Х и Y являются двумя выборками из одной генеральной совокупности, то есть данные однородны. Если это так, то отдельные ранги (или значения) из обоих рядов должны чередоваться, когда эти два ряда объединены в один общий ряд. Пусть, например, ранги (или значения) рядов X и Y будут: x1, x2, x3, x4, x5 и y1, y2, y3, y4, y5, y6. Тогда расположение x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, y6 будет противоречить нулевой гипотезе. Гораздо больше соответствует гипотезе Н0 расположение вида: x1, x2, y1, y3, x4, y2, y3, y4, y5, x5, y6. Количественным показателем, по которому можно отличить оба эти распределения друг от друга, может служить число серий S, каждая из которых есть непрерывная последовательность наблюдений, принадлежащих к одному из двух рядов. Так, первое расположение состоит из двух серий, а второе расположение - из шести серий. Серийный критерий различия между двумя совокупностями основан на том, что нулевая гипотеза отвергается, если число серий слишком мало (в данном случае применяется односторонний критерий). Методы теории вероятности позволяют вычислить вероятность того или иного числа серий при заданном числе наблюдений в каждом из рядов (нулевая гипотеза справедлива). И наоборот, можно указать число серий, отвечающих тому или иному уровню значимости (например, 0,05 или 0,01). В таблице приводятся граничные значения числа серий при α=0,05. Приближенно можно считать, что  Нулевая гипотеза отвергается при  и не отвергается при  При малых объемах выборок серийный критерий оказывается недостаточно чувствительным. В таких случаях, а также, если  , следует проверить результат при помощи наиболее строгого критерия однородности Колмогорова-Смирнова.Пример проверки гипотезы при помощи U-критерия серий Вальда—Вольфовица. Для проверки эффективности новой добавки к кормам цыплят оценивали дневной привес у контрольной  и экспериментальной  групп.
Расположим все значения в один возрастающий ряд, помещая для ясности наблюдения по  и  в разных строках:
Имеется пять серий (  ). Из таблицы критических значений (приложение 3) находим  , а значение  . Так как  , то вопрос о справедливости нулевой гипотезы остается открытым.5.5.3 Сравнение двух независимых выборок. Тест Колмогорова-Смирнова Данный критерий позволяет оценить существенность различий между двумя выборками. Его применение возможно также для сравнения эмпирического распределения с теоретическим. Объёмы рассматриваемых выборок должны быть достаточно большими:  ≥50,  ≥50. Для использования теста выборки должны быть представлены в виде частотного распределения, при этом число категорий должно быть небольшим (до 7-9).Нулевая гипотеза H0={различия между двумя распределениями недостоверны}. Критерий позволяет найти категорию, в которой сумма частот расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения. Алгоритм проверки:
Схематично алгоритм применения критерия Колмогорова-Смирнова можно представить следующим образом: 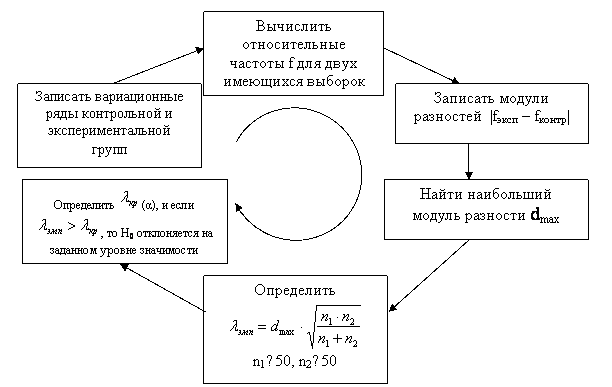 Пример сравнения двух независимых выборок с использованием теста Колмогорова-Смирнова Являются ли значимыми различия между творческой активностью контрольной и экспериментальной группами студентов?
Вычисляем относительные частоты  , равные частному от деления частот на объём выборки, для каждой из имеющихся выборок.Определяем модуль разности соответствующих относительных частот для контрольной и экспериментальной выборок. В результате исходная таблица примет следующий вид:
Среди полученных модулей разностей относительных частот выбираем наибольший модуль, который обозначается  =0.18.Эмпирическое значение критерия λэмп определяется с помощью формулы:  Считая, что , по таблице (приложение 4) определяем критическое значение критерия:  .  , следовательно, нулевая гипотеза отвергается, и группы по рассмотренному признаку отличаются существенно.5.6 Сравнение двух зависимых выборок Имеются данные обследования, полученные в двух опытах (или в двух замерах), но на одной и той же группе единиц совокупности. Две выборки считаются зависимыми, если каждому значению одной выборки однозначно ставится в соответствие ровно одно значение другой выборки. Зависимые (связанные, попарно сопряженные) выборки - это выборки, представляющие собой параметры одной и той же совокупности до и после воздействия некоторого фактора. Чаще всего зависимые выборки – это измерения одной и той же группы объектов в разные моменты времени (например, до и после воздействия какого-либо фактора). Таким образом, зависимые выборки всегда должны содержать одинаковое количество наблюдений. Для того чтобы доказать эффективность воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Сдвигом называется разность между значениями измеряемого параметра «после» и «до» проведения эксперимента. Наиболее часто для сравнения зависимых выборок используют параметрический тест – -критерий Стьюдента и непараметрические тесты – критерий знаков и критерий Уилкоксона.Критерий знаков - это непараметрический тест, использующийся фактически для сравнения медианы распределения с каждым конкретным значением. Критерий знаков предъявляет к тестируемой выборке только одно требование: шкала измерений должна быть порядковой, интервальной или относительной (т.е. тест нельзя применять к номинальным переменным). Других ограничений (в том числе и на форму распределения) нет. С одной стороны, это делает тест настолько широко применимым, насколько это вообще возможно. С другой - снижает его мощность, поскольку тест не может опираться в своей работе на какие-либо предположения о свойствах анализируемого распределения. Невысокая мощность критерия знаков особенно сильно проявляется на небольших выборках. Это является следствием того, что тест использует информацию только о положении элементов выборки относительно предполагаемой медианы: слева или справа. Информация об их сравнительной величине тестом не используется. В то же время, есть более мощный тест - W-критерий Уилкоксона, использующий информацию о ранге элементов в выборке. К сожалению, сфера применения этого теста ограничена распределениями, симметричными относительно медианы. Для несимметричных распределений он дает некорректные результаты, так что в нашем распоряжении остается только менее мощный критерий знаков. 5.6.1 Сравнение двух зависимых выборок с использованием теста знаков Одним из наиболее простых критериев различия является критерий знаков G. Он дает возможность установить, насколько однонаправленно изменяются значения признака при повторном измерении связанной однородной выборки. Критерий знаков применяется к данным, полученным в ранговой, интервальной шкале и шкале отношений. В случаях, когда сдвиги могут быть определены количественно, но варьируются в достаточно широком диапазоне, лучше применять критерий Вилкоксона. Нулевая гипотеза: H0={преобладание типичного направления сдвига является случайным}. Альтернативная гипотеза – H1={преобладание типичного направления сдвига не является случайным}. Алгоритм проверки:
Количество измерений должно быть не меньше 5 и не больше 300. При равенстве типичных и нетипичных сдвигов критерий знаков неприменим. Схематично алгоритм применения критерия знаков можно представить следующим образом: 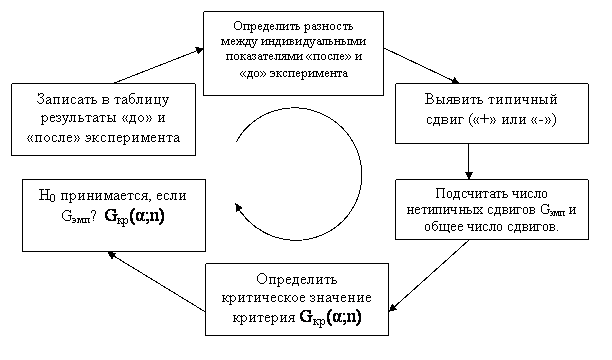 Пример сравнения двух зависимых выборок с использованием теста знаков Результаты измерения уровня тревожности до и после проведения тренинга в группе испытуемых отображены в таблице.
Определить, является ли изменение уровня тревожности статистически значимым. Число положительных сдвигов превосходит количество сдвигов в отрицательном направлении, следовательно, типичным является положительный сдвиг. Эмпирическое значение критерия определяется, как число нетипичных сдвигов и равно 5. Критическое значение критерия  (приложение 5). Так как  , то нулевая гипотеза не отвергается. Типичный сдвиг считается случайным на выбранном уровне значимости. |
.
:
, где 
– общее число сдвигов, т.е. объем выборки, определяют по специальной таблице.