лекция. Радианная мера угла. Тема Радианная мера угла. Вращательное движение. Синус, косинус, тангенс и котангенс числа

• Название: Тема Радианная мера угла. Вращательное движение. Синус, косинус, тангенс и котангенс числа
• Анкор: лекция
• Дата: 08.03.2021
• Размер: 439.37 Kb.
• Имя файла: Радианная мера угла.docx
• Тип: Документы; #182619

Тема: Радианная мера угла. Вращательное движение. Синус, косинус, тангенс и котангенс числа

1. 
   Радианная мера угла. Вращательное движение.
   

Градусная мера.Здесь единицей измерения является градус (обозначение °) – это поворот луча на 1 / 360 часть одного полного оборота. Таким образом, полный оборот луча равен 360°. 

1/60 часть градуса называется минутой (обозначают 1^').

1/60 часть минуты называется секундой (обозначают 1^'').
Радианная мера.  

 Радианная мера измерения угла есть отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к радиусу дуги.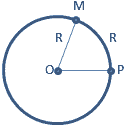



Градусная мера угла в 1 радиан равна: Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.


Так как π = 3,14, то 1 рад = 57,3°

Если угол содержит α  радиан, то его градусная мера равна



И наоборот



Наиболее активные студенты участвуют при решении примеров на поиск радианной и градусной меры угла.
Пример 1.

Найти радианную меру угла равного 1) 30°, 2)135°

Решение:

1) 30° = 30·π / 180 = π/6

2) 135° = 135·π/180 = 3π/4
Пример 2.

Найти градусную меру угла выраженного в радианах 1) π/3 , 2) 4·π/5

Решение:

1) π/3 = 180°/3 = 60°

2) 4π/5 = 4·180°/5 = 144°
Практические задания
№1: Переведите в радианную меру углы:

1) 45° 4) 100° 7) 215°

2) 15° 5) 200° 8) 150°

3) 72° 6) 360° 9) 330°
№2: Переведите в градусную меру углы: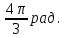




1) 3) 5)

2 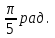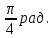) 4) 6)

2. 
   Синус, косинус, тангенс и котангенс числа
   

Острый угол в прямоугольном треугольнике

Из курса геометрии известны определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Они даются как отношение сторон прямоугольного треугольника. Приведем их формулировки.

Определение.

Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.

Определение.

Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.

Определение.

Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.

Определение.

Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.

Там же вводятся обозначения синуса, косинуса, тангенса и котангенса – sin, cos, tg и ctg соответственно.

Давайте найдем значения синуса, косинуса, тангенса и котангенса углов 30°,45° и 60°.





Запишем все значения углов в таблицу: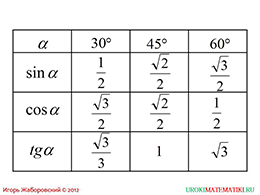



Предлагаю вам алгоритм, благодаря которому вы легко, в течение минуты восстановите в памяти все вышеуказанные значения:
1. Записываем в строчку углы от 0 до 90 градусов. Слева в столбик запишем сначала синус, затем косинус аргумента:



2. Напротив синуса пишем числа от нуля до четырёх (под значениями  углов). Напротив косинуса от 4 до 0:



3. Далее извлекаем корень:



4. Делим на 2:



5. Вычисляем: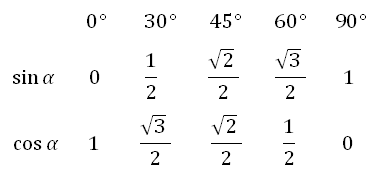



Мы получили значения синуса и косинуса углов от 0 до 90 градусов. Далее, зная формулы тангенса и  котангенса: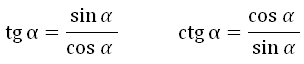



вы сможете найти  значения для указанных углов.

Например:




6.Решение задач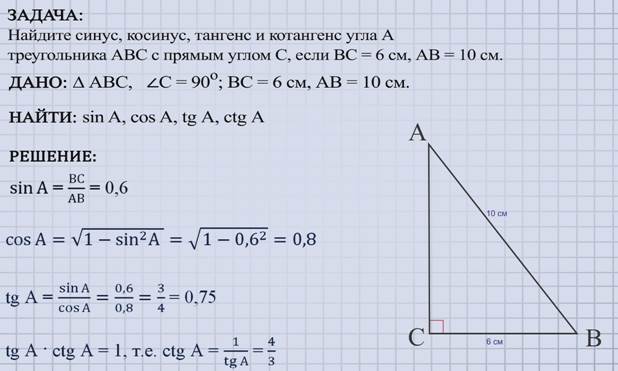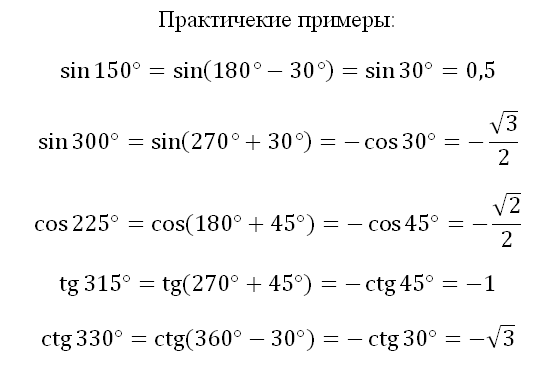





8. Практическая работа

Вычислить:
а) sin 30⁰; cos 30⁰; tg 30⁰; ctg 30^0;
б) sin 150⁰; cos 150⁰; tg 150⁰; ctg 150⁰;
в) sin 210⁰; cos 210⁰; tg 210⁰; ctg 210⁰;
г) sin 240⁰; cos 240⁰; tg 240⁰; ctg 240⁰.