С-21 Системы счисления. Тема Системы счисления. Непозиционные и позиционные системы счисления. Позиционные и непозиционные системы счисления

• Название: Тема Системы счисления. Непозиционные и позиционные системы счисления. Позиционные и непозиционные системы счисления
• Дата: 12.02.2021
• Размер: 54.06 Kb.
• Имя файла: С-21 Системы счисления.docx
• Тип: Документы; #175974

Тема: Системы счисления. Непозиционные и позиционные системы счисления.

1. Позиционные и непозиционные системы счисления

Системой счисления называется совокупность приемов и правил для записи чисел цифровыми знаками. Любая предназначенная для практического применения система счисления должна обеспечивать:

• 
  возможность представления любого числа в рассматриваемом диапазоне величин;
  
• 
  единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);
  
• 
  простоту оперирования числами.
  

Все системы представления чисел делят на позиционные и непозиционные.

Непозиционная система счисления – система, для которой значение символа не зависит от его положения в числе.

Для их образования используют в основном операции сложения и вычитания. Например, система с одним символом-палочкой встречалась у многих народов. Для изображения какого-то числа в этой системе нужно записать количество палочек, равное данному числу. Эта система неэффективна, так как запись числа получается длинной. Другим примером непозиционной системы счисления является римская система, использующая набор следующих символов: I, V, X, L, C, D, M и т. д. В этой системе существует отклонение от правила независимости значения цифры от положения в числе. В числах LX и XL символ X принимает два различных значения: +10 – в первом случае и –10 – во втором случае.

Позиционная система счисления – система, в которой значение символа определяется его положением в числе: один и тот же знак принимает различное значение. Например, в десятичном числе 222 первая цифра справа означает две единицы, соседняя с ней – два десятка, а левая – две сотни.

Любая позиционная система характеризуется основанием. Основание (базис) позиционной системы счисления – количество знаков или символов, используемых для изображения числа в данной системе.

Для позиционной системы счисления справедливо равенство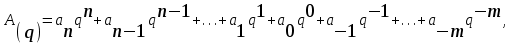

(1)
где A_(q) – произвольное число, записанное в системе счисления с основанием q; a_i – коэффициенты ряда (цифры системы счисления); n, m – количество целых и дробных разрядов.

На практике используют сокращенную запись чисел: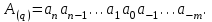

( 2)
Например:

а) в двоичной системе (q=2)

11010.101₂ = 1 · 2⁴ + 1 · 2³ + 0 · 2² + 1 · 2¹ + 0 · 2⁰ + 1 · 2^-1 + 0 · 2^-2 + 1 · 2^-3;

б) в троичной системе (q=3)

22120.212₃ = 2 · 3⁴ + 2 · 3³ + 1 · 3² + 2 · 3¹ + 0 · 3⁰ + 2 · 3^-1 + 1 · 3^-2 + 2 · 3^-3;

в) в шестнадцатиричной системе (q=16)

A3F.1CD₁₆ = A · 16² + 3 · 16¹ + F · 16⁰ + 1 · 16^-1 + C · 16^-2 + D · 16^-3.

Контрольные вопросы:

1. 
   Что обеспечивает система счисления?
   
2. 
   Какая система счисления называется позиционной?
   
3. 
   Какая система счисления называется непозиционной?
   
4. 
   Какое равенство отожествляется с позиционной системой счисления?
   
5. 
   Приведите примеры позиционных и непозиционных систем счисления.
   

Тема: Перевод чисел из заданной системы в другую.

1. 
   Методы перевода чисел
   

Числа в разных системах счисления можно представить следующим образом: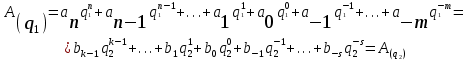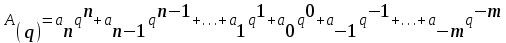





где

Значит, в общем виде задачу перевода числа из системы счисления с основанием q₁ в систему счисления с основанием q₂ можно представить как задачу определения коэффициентов b_j нового ряда, изображающего число в системе с основанием q₂. В такой постановке задачу перевода можно решить подбором коэффициентов b_j.

Перевод чисел делением на основание новой системы

Перевод целых чисел осуществляется делением на основание q₂ новой системы счисления, правильных дробей – умножением на основание q₂. Действия деления и умножения выполняются по правилам q₁-арифметики. Перевод неправильных дробей осуществляется раздельно по указанным правилам, результат записывается в виде новой дроби в системе с основанием q₂.

Пример 1. Перевести десятичное число A = 61₁₀ в систему счисления с q = 2.
61 | 2

60 30 | 2

b₀ = 1 30 15 | 2

b₁ = 0 14 7 | 2

b₂ = 1 6 3 | 2

b₃ = 1 2 1 = b₅

b₄ = 1

Ответ: 61₁₀ = 111101₂.

Табличный метод перевода

В простейшем виде табличный метод заключается в следующем: имеется таблица всех чисел одной системы с соответствующими эквивалентами из другой системы; задача перевода сводится к нахождению соответствующей строки таблицы и выбору из нее эквивалента. Такая таблица очень громоздка и требует большой емкости памяти для хранения.

Другой вид табличного метода заключается в том, что имеются таблицы эквивалентов в каждой системе только для цифр этих систем и степеней основания (положительных и отрицательных); задача перевода сводится к тому, что в выражение ряда (1) для исходной системы счисления надо поставить эквиваленты из новой системы для всех цифр и степеней основания и произвести соответствующие действия (умножения и сложения) по правилам q₂-арифметики. полученный результат этих действий будет изображать число в новой системе счисления.

Пример 2. Перевести десятичное число A = 113 в двоичную систему счисления, используя таблицу эквивалентов цифр и степеней основания

(q₂ = 2).
Таблица 1 – Таблица эквивалентов

Десятичное число	Двоичное число
100	0001
101	1010
102	110 0100

Решение. Подставив значения двоичных эквивалентов десятичных цифр и степеней основания в (3), получим

A = 113 = 1 · 10² + 1 · 10¹ + 3 · 10⁰ = 001 · 1100100 + 0001 · 1010 + 0011 · 0001 = 1110001₂.

Ответ: 1110001₂.

2. 
   Форматы представления чисел с фиксированной и плавающей запятой
   

Число 0,028 можно записать так: 28·10^-3, или 2,8·10^-2, или 0,03 (с округлением) и т. д. В компьютере используются две формы представления чисел.

Представление чисел с фиксированной запятой (точкой). Оно характеризуется тем, что положение разрядов числа в машинном изображении остается всегда постоянным независимо от величины самого числа.

Число А можно представить в виде
A=[A]_ф K_A,
где [A]_ф – машинное изображение числа в формате с фиксированной запятой, значение которого лежит в пределах
-1 < [A]_ф < 1;
K_A – масштабный коэффициент, выбирается так, чтобы сохранить соответствие разрядов всех чисел, которыми оперирует компьютер.

Формат (разрядная сетка) машинного изображения чисел с фиксированной запятой разбивается на знаковую часть и поле числа. В знаковую часть записывается информация о знаке числа: 0, если A≥0; 1, если A<0.

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

№ разряда

Знаковая часть

Поле числа

Например, числа А₁ и A₂ в прямом коде имеют машинное изображение:

0

0

1

0

0

1

1

1

0

0

0

1

0

1

1

1

A₁ = 0.010011100010111₂;

1

0

1

0

0

1

1

1

0

0

0

1

0

1

1

1

A₂ = – A₁ = 0.010011100010111_2.

Представление чисел в формате с плавающей запятой. Оно характеризуется тем, что положение разряда числа в его машинном изображении непостоянно, и число А записывается следующим образом:

A = m_Ap_A,
где m_A – мантисса числа A; при представлении числа в компьютере мантисса должна удовлетворять ограничению 2^-1 ≤ | m_A | ≤ 1 – 2^-n; n – количество разрядов для изображения мантиссы без знака; p_A – порядок числа A.

Формат машинного изображения числа с плавающей запятой содержит знаковые части и поля мантиссы и порядка.

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

№ разряда

Форматы данных и машинные коды чисел.

Числа в компьютерах в двоичных кодах представляются как с фиксированной точкой или запятой, так и с плавающей точкой или запятой. Представление чисел в формате с фиксированной точкой получило название естественной формы числа, представление с плавающей точкой – нормальной формы числа. Под те или иные форматы отводится заранее известное количество разрядов (бит) -16,32 и т.д. Эта же величина может быть выражена в байтах, с учетом того, что 1 байт=8 бит.

Представление чисел в формате с фиксированной точкой

Для чисел в естественной форме положение точки жестко фиксируется:

• 
  Для целых чисел точка располагается справа от младшего разряда:
  

0000000000000000₂ =0₁₀, 0111111111111111_{. 2}=32767.₁₀;

• 
  Для правильных дробей – перед старшим разрядом:
  

0.000000000000000₂=0₁₀, 0.000000000000001₂=0.000 030 517 578₁₀;

• 
  Для смешанных дробей – в определенном месте, отделяющем целую часть числа от дробной:
  

000000.0000000000₂=0.0₁₀, 000001.0000000001₂=1.000 976 563₁₀

Наиболее часто такая форма используется для целых чисел и целых чисел без знака. Количество разрядов может быть либо 16 (вид Н), либо 32 (вид F).

Во всех форматах знак числа помещается в старший разряд и кодируется как 0 – знак положительного числа, либо как 1 – знак отрицательного числа. Знак отделяется от самого числа воображаемой точкой (рис.)

Знак 2¹⁴ 2¹³ 2¹ 2⁰

	1	1	1		1	1	Аmin
Формат Н				…
	0	1	1		1	1	Аmax
	0	1	2	…	14	15

Знак 2³⁰ 2²⁹ 2¹ 2⁰

	1	1	1		1	1	Аmin
Формат F				…
	0	1	1		1	1	Аmax
	0	1	2	…	14	15

Рис. 1.3. Форматы чисел с фиксированной точкой.
Фиксированная точка позволяет задать число только в строго определенном диапазоне. В формате Н числа можно задавать

От 1111 1111 1111 1111₂ до 0111 1111 1111 1111₂,

т.е. от -32767₁₀ до 32767₁₀, или от (1 – 2¹⁵ ) до (2¹⁵-1).

В формате F числа могут находиться в интервале

От 1111 1111 1111 1111 1111 1111 1111 1111₂

До 0111 1111 1111 1111 1111 1111 1111 1111₂,

т.е. от -7 F F F F F F F₁₆ до 7 F F F F F F F₁₆.

Естественно, что представление в шестнадцатиричной системе для формы F предпочтительнее двоичной.

Рассмотрим несколько примеров.

ЗАДАЧИ

1.3.1. Представить в форматах Н и F числа -127₁₀ и 127₁₀

127₁₀=1*2⁶+1*2⁵+1*2⁴+1*2³+1*2²+1*2¹+1*2⁰=0111 1111₂.

А₂^Н=0000 0000 0111 1111_2, А₂^F=0000 00 7 F₁₆.

-127₁₀=- (1*2⁶+1*2⁵+1*2⁴+1*2³+1*2²+1*2¹+1*2⁰)= -0111 1111₂.

А₂^Н=1000 0000 0111 1111_2, А₂^F=8000 00 7 F₁₆.
1.3.2. Определить, какие из следующих шестнадцатиричных чисел положительные, а какие отрицательные: 9754, 157, ADF, 7654AD и DFEA.

Знак числа определяется по первой цифре: если она меньше 8 (1000), то число положительное, если значение от 8 до F, то отрицательное. Таким образом, получаем 9754<0, 157>0, ADF<0, 7654AD>0 и DFEA<0.

Представление чисел в формате с плавающей точкой

Для расширения диапазона рассматриваемых чисел по сравнению с естественной формой чисел используется формат с плавающей точкой или нормальная форма. Любое число в этом формате представляется, как А= ±m_aE^±Pа,

где m_a - мантисса числа А; Е – основание системы счисления; ±Р_а- порядок. Все эти величины – двоичные числа без знака. На рис. 2 приведен формат числа в нормальной форме. Старший разряд (нулевой) содержит знак мантиссы, первый разряд – знак порядка, 6 разрядов, со второго по седьмой, определяют значение порядка, а остальные – мантиссу. Нормальная форма может быть представлена коротким форматом Е (4 байта), длинным форматом D (8 байт) и повышенной точности (16 байт). Во всех этих формах представления первый байт остается постоянным, изменяется только область, отведенная под мантиссу.
Знак m_a Знак Р_а Порядок Мантисса

Знак ma

Знак Ра

Ра

ma

0 1 2 … 7 8 31

Рис. 2. Нормальная форма числа
При таком представлении чисел 0 может быть записан 64 разными способами, т.к. для этого подходят любые значения порядков 0*2⁰=0*2¹=…=0*2⁶³. А другие числа могут иметь много различных форм записи. Например, 1536₁₀=3*2⁹=6*2⁸=…=768*2¹.

Для однозначного представления чисел мантиссу нормализуют, т.е. накладывают ограничение 1/Е≤m<1.

Это ограничение означает, что мантисса представляет собой правильную дробь и содержит хотя бы одну значащую цифру после запятой, отличную от нуля. Нормализованным представлением нуля является такое представление, при котором во всех разрядах находятся нули.

При использовании нормальной формы для части компьютеров характерно смещение оси порядков в область положительных значений. В этом случае арифметические действия производятся над порядками, не имеющими знака. В нормальной форме под значение порядка отводится 7 разрядов, один из них знаковый. Таким образом, значение порядка может лежать в интервале 2⁶≤Р≤2⁶-1, т.е. от -64 до 63.

Сместив порядок на 2⁶=64=40₁₆, мы получаем интервал возможных значений 0≤Р≤2⁷-1=127. Смещенный порядок на 40₁₆ называется характеристикой и вычисляется как Рx=P+40.

Если характеристика равна 40, то порядок равен 0; если характеристика меньше 40, то порядок отрицателен; если больше – то положителен.

ЗАДАЧИ

1.3.3. Представить в нормальной сетке Е числа 32001,5₁₀ и -32001,5₁₀
Представим числа в шестнадцатиричном коде 32001,5₁₀=7D01,8₁₆и

-32001,5₁₀. =-7D01,8₁₆

Затем найдем нормализованные мантиссы и характеристики.

m=7D01,8₁₆ m=0,7D018,

при этом характеристика становится равной Рx=40+4=44

Знак mРx m

0

100 0100

0111 1101 0000 0001 1000 0000

447D0180>0

m=-7D01,816 m=-0,7D018,

при этом характеристика становится равной Рx=40+4=44

Знак mРx m

1

100 0100

0111 1101 0000 0001 1000 0000

С47D0180<0

Контрольные вопросы:

1. 
   Как осуществляется перевод чисел делением на основание новой системы.
   
2. 
   Как пользуются при табличном методе перевода чисел?
   
3. 
   Что понимают под форматом данных?
   
4. 
   Как представляется число в формате с фиксированной точкой?
   
5. 
   Как представляется число в формате с плавающей точкой?