Тема 1. Случайные события
Найти средний балл учащихся, которые во время экзамена получили следующие оценки: 5; 3; 4; 5; 3; 2; 3; 5; 4; 3
|
3,7
|
Дискретная случайная величина Х имеет закон распределения вероятностей: (x=5;7 p=0,3;0,7):
|
6,4
|
Несовместными являются следующие события
|
появление валета и дамы при однократном взятии одной карты из колоды;
|
В урне имеется 5 белых и 7 черных шаров. Из урны вынимают одновременно два шара. Вероятность того, что оба шара окажутся белыми, равна:
|
5/33
|
Игральный кубик подбрасывают один раз. Событие А – “выпало число очков, большее двух”; событие В – “выпало число очков, меньшее пяти”. Верным является утверждение:
|
события А и В совместны
|
Игральный кубик подбрасывают один раз. Вероятность того, что на верхней грани выпадет четное число очков, равна:
|
1/2
|
Вероятность наступления некоторого события может быть равной:
|
0,6
|
Дана плотность вероятности непрерывной случайной величины X:
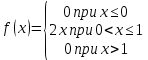
Найдите вероятность того, что в результате испытания X примет значения, принадлежащее интервалу (0,3;1)
|
0,91
|
Математическое ожидание M(Y) случайной величины Y = 2X + 4 при M(X) = 3 равно:
|
10
|
Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей
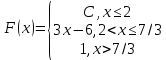
Тогда значение С равно ...
|
0
|
Первый студент успешно ответит на данный вариант тестов с вероятностью 0,5, а второй – с вероятностью 0,4. Вероятность того, что оба студента успешно пройдут тестирование, равна:
|
0,2
|
Математическое ожидание разности двух случайных величин равна:
|
разности математических ожиданий этих случайных величин
|
Если события А и В несовместны, то справедлива формула:
|
P(A+B)=P(A)+P(B)
|
Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей
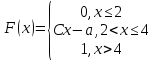
Тогда значение С равно ...
|
C=1/2, a=1
|
Постоянный множитель из под знака дисперсии ...
|
Можно внести в квадрат и вынести
|
Дисперсия случайной величины характеризует...
|
рассеивание случайной величины относительно среднего значения
|
Формула 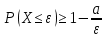 выражает выражает
|
Неравенство Маркова
|
В партии из 10 изделий 8 изделий являются бракованными. Вероятность того, что при выборочном контроле из 5выбранных изделий бракованными окажутся 3 изделий (С - символ числа сочетаний):
|
2/9
|
Формула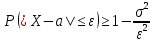 выражает выражает
|
Неравенство Чебышева
|
Математическое ожидание случайной величины имеет размерность
|
самой случайной величины
|
Формула 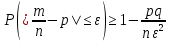 выражает выражает
|
Теорему Бернулли
|
Случайная величина равномерно распределена на интервале [-2,2]. Тогда ее плотность вероятности принимает значение, равное
|
1/4
|
Дискретная случайная величина X имеет закон распределения:
(X=7;14;21;28 P=0,1;0,2 Pз=0,4):
Вероятность Pз равна:
|
0,3
|
Непрерывная случайная величина Х задана дифференциальной функцией распределения вероятностей
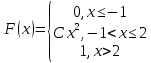
Тогда значение С равно ...
|
1/3
|
Первый студент успешно ответит на данный вариант тестов с вероятностью 0,5, а второй – с вероятностью 0,7. Вероятность того, что оба студента успешно пройдут тестирование, равна:
|
0,35
|
В урне имеется а белых и b черных шаров. Из урны вынимают (одновременно или последовательно) два шара. Вероятность того, что оба шара окажутся белыми, равна:
|
a*(a-1)/(a+b)*(a+b-1)
|
Несовместными являются следующие события
|
появление герба и цифры при однократном подбрасывании одной монеты;
|
Первый стрелок попадает в мишень с вероятностью 0,9, а второй – с вероятностью 0,5. Каждый стрелок делает по одному выстрелу. Вероятность того, что оба стрелка попадут в мишень, равна:
|
0,45
|
Количество различных способов выбора (порядок не имеет значения) 3 томов из 8-томного собрания сочинений равно:
|
56
|
Количество комбинаций, которые можно получить путем перестановки букв, входящих в слово “число”, равно:
|
120
|
Если события А и В совместны, то справедлива формула:
|
P(A+B)<=P(A)+P(B)
|
Число пятизначных чисел, одинаково читающихся слева направо и справа налево равно...
|
900
|
Имеется 10 качественных и 4 бракованных изделий. Извлекается одно изделие. Событие А – “извлечено качественное изделие”, событие B – “извлечено бракованное изделие”. Для этих событий неверным является утверждение:
|
вероятность события А равна вероятности события В;
|
В партии из N изделий М изделий являются бракованными. Вероятность того, что при выборочном контроле из n выбранных изделий бракованными окажутся m изделий (m< n; С - символ числа сочетаний):
|
верхний правый член числителя (С(N-M))^n-m
|
Игральный кубик подбрасывают один раз. Событие А – “выпало число очков, большее трех”; событие В – “выпало число очков, меньшее трех”. Верным является утверждение:
|
события А и В несовместны
|
Вероятность для студента сдать первый экзамен равна 0,6, второй — 0,4. Вероятность сдать либо первый, либо второй, либо оба экзамена равна:
|
0,76
|
Игральный кубик подбрасывают один раз. Вероятность того, что на верхней грани выпадет число очков, равное двум или четырем, равна:
|
1/3
|
Вероятность наступления некоторого события не может быть равной:
|
3
|
Вероятность изготовления нестандартной детали равна 0,11. Пользуясь формулой Бернулли найти вероятность того, что из пяти наудачу взятых деталей будут четыре стандартных.
|
0,345
|
В вопросах к зачету имеются 75% вопросов, на которые студенты знают ответы. Преподаватель выбирает из них два вопроса и задает их студенту. Определить вероятность того, что среди полученных студентом вопросов есть хотя бы один, на который он знает ответ
|
0,937
| Тема 2. Случайные величины
Дисперсия разности двух независимых случайных величин равна:
|
разности дисперсий этих случайных величин
|
Дискретная случайная величина задана законом распределения вероятностей, тогда ее математическое ожидание равно 1,7, если ... X -2 1 3 P 0,1 a b
|
a=0,3, b=0,6
|
Дисперсия случайной величины имеет размерность
|
квадрата случайной величины
|
Математическое ожидание M(Y) случайной величины Y = 5 X - 3 при M(X) = 2 равно:
|
7
|
Дискретная случайная величина X имеет закон распределения:
|
(X=2;4; P=0,2;0,8):
|
Математическое ожидание M(X) этой случайной величины равно:
|
0,2
|
Дискретная случайная величина Х имеет закон распределения вероятностей: (x=5;7 p=0,3;0,7):
|
3,6
|
Математическое ожидание случайной величины характеризует...
|
среднее значение случайной величины
|
Найти средний балл учащихся, которые во время экзамена получили следующие оценки: 5; 4; 4; 5; 3; 2; 3; 5; 5
|
4
|
Дискретная случайная величина Х имеет закон распределения:
Вероятность Pз равна:
(X=2;4;7;11 P=0,1;0,2 Pз=0,5):
|
0,2
|
Найти моду для заданного ряда оценок, полученных учащимися на экзамене: 5; 4; 4; 5; 3; 2; 3; 5; 5
|
5
|
Как называется наиболее вероятное значение случайной величины X?
|
Модой
|
Ряд распределения дискретной случайной величины характеризует:
|
соответствие между значениями случайной величины и их вероятностями
|
Постоянный множитель из под знака математического ожидания ...
|
Можно вынести
|
Функция распределения случайной величины определяется как:
|
вероятность попадания случайной величины в область левее (менее) заданного значения
|
Найти медиану для заданного ряда оценок, полученных учащимися на экзамене: 5; 4; 4; 5; 3; 2; 3; 5; 5
|
4
|
Дано следующее распределение дискретной случайной величины Х
(X=1;2;4;5 P=0.31;0.1;0.29;0.3)
Найти ее математическое ожидание, дисперсию и среднеквадратичное отклонение, используя формулы для их определения.
|
М(х) = 3,17; Д(х) = 2,80; 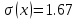
|
Как называется сумма произведений всех значений дискретной случайной величины X на соответствующие им вероятности?
|
Математическим ожиданием
|
Дискретная случайная величина Х имеет закон распределения вероятностей: (x=2;4 p=0,2;0,8):
Математическое ожидание M(X) этой случайной величины равно:
|
3,6
| Тема 3. Законы распределения
На рисунке изображены четыре кривые, характеризующие случайные величины с гауссовскими плотностями вероятности p(x) и одинаковыми математическими ожиданиями, равными m. Наибольшее значение дисперсии соответствует кривой:
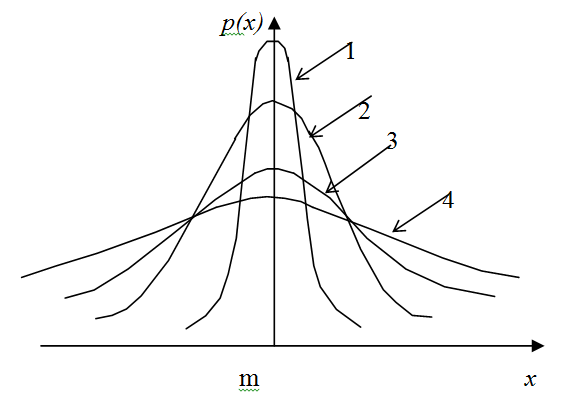
|
4
|
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале (-1;5), имеет вид:
Тогда значение a равно...
|
1/6
|
Что представляет собой закон больших чисел?
|
общий принцип, в силу которого совокупное действие большого числа факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая
|
Непрерывная случайная величина Х задана дифференциальной функцией распределения вероятностей
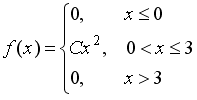
Тогда значение С равно ...
|
1/9
|
График плотности распределения вероятностей f(x) случайной величины приведен на рисунке (4/3;0,5)
Тогда значение a равно ...
|
1
|
Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей

Тогда значение С равно …
|
0
|
Какой закон распределения имеет непрерывная случайная величина X на отрезке [a, b], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его?
|
равномерный закон распределения
|
Дана плотность вероятности непрерывной случайной величины X:
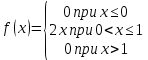
Найдите вероятность того, что в результате испытания X примет значения, принадлежащее интервалу (0,5;1)
|
0,75
|
График плотности распределения вероятностей непрерывной случайной величины Х, распределенной равномерно в интервале (-2;3), имеет вид (см. рисунок). Тогда значение а равно...
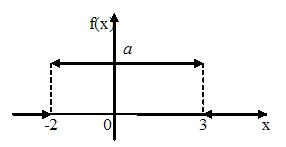
|
0,2
|
График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале (-1;3), имеет вид:
Тогда значение а равно...
|
0,25
|
Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей
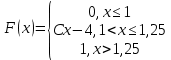
Тогда значение С равно …
|
4
|
Изизображенных на рисунке кривых линий F(x) в качестве функции распределения случайной величины с математическими ожиданием m может рассматриваться
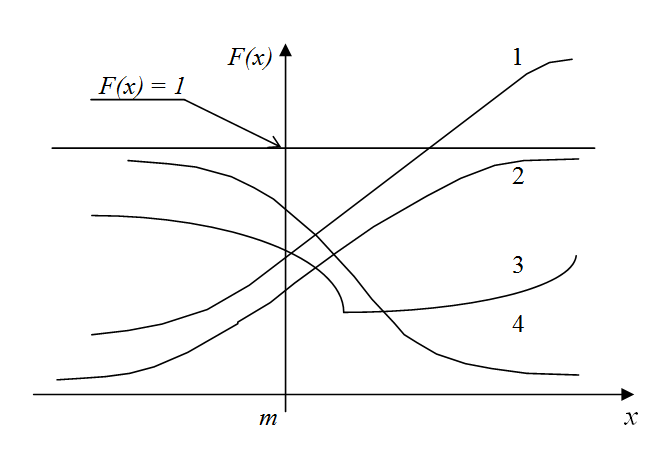
|
2
|
Случайная величина равномерно распределена на интервале [0; 4]. Тогда ее плотность вероятности принимает значение, равное
|
1/4
| |
 Скачать 82.31 Kb.
Скачать 82.31 Kb.