Копия Выпуклые и вогнутые функции.. Тема Выпуклые и вогнутые функции. Их основные свойства. Выпуклые и вогнутые функции
 Скачать 96 Kb.
|
Тема: Выпуклые и вогнутые функции. Их основные свойства.§1. Выпуклые и вогнутые функции.Определение 1. Функция f(X), определенная на выпуклом множестве M, называется выпуклой, если для любых двух точек X1 и X2 из этого множества и любого 0 ≤ λ ≤ 1 справедливо неравенство: f[λX1 + (1 - λ)X2] ≤ λf(X1) + (1 – λ)f(X2) (1) Функция называется строго выпуклой, если в условии (1) при 0 < λ < 1 и любых X1, X2  M, X1 ≠ X2 имеет место строгое неравенство « < ».Определение 2. Функция f(X), определенная на выпуклом множестве M называется вогнутой, если для любых двух точек X1и X2 из этого множества и любого 0 < λ < 1 справедливо неравенство: f[λX1 + (1 – λ)X2] ≥ λf(X1) + (1 – λ)f(X2) (2). Если в условии (2) при 0 ≤ λ ≤ 1 и любых X1, X2 M, X1 ≠ X2 имеет место строгое неравенство « > », то f(X) называется строго вогнутой.Если функция f(X) – выпуклая, то « – f(X)» – вогнутая функция и наоборот. Выпуклость и вогнутость функций определяется только относительно выпуклых множеств, так как по определению выпуклого множества ему вместе с точками X1 и X2 принадлежат и все точки вида: λX1 + (1–λ)X2 при 0 ≤ λ ≤ 1. Если Z = f(X) – выпуклая поверхность ( n ≤ 2) , то отрезок, соединяющий любые две ее точки лежит на поверхности или выше ее. ЕслиZ= f(X) – вогнутая, то отрезок лежит на поверхности или ниже ее. 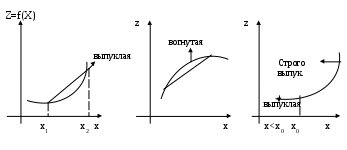 Выпуклая функция f(X) не может принимать на отрезке [X1,X2] значений больших, чем линейная функция интерпретирующая значения f(X1) и f(X2). Сумма выпуклых функций есть функция выпуклая: F(X) =  , если fj(X) –выпуклые, то и F(X) – выпуклая.Справедливо такое утверждение: сумма выпуклых функций есть функция выпуклая. Теорема 1. Если g(x) – выпуклая функция при всех x ≥ 0, то будем выпуклым и множество решений системы g(x) ≤ b, x ≥ 0. Доказательство. Покажем, что вместе с решением x1 и x2 системы множеству решений системы будет принадлежать и их выпуклая линейная комбинация, то есть  , где 0 ≤ λ ≤ 1. Ясно, что  . Покажем, что  ≤ b.Так как функция g(x) – выпуклая:  (3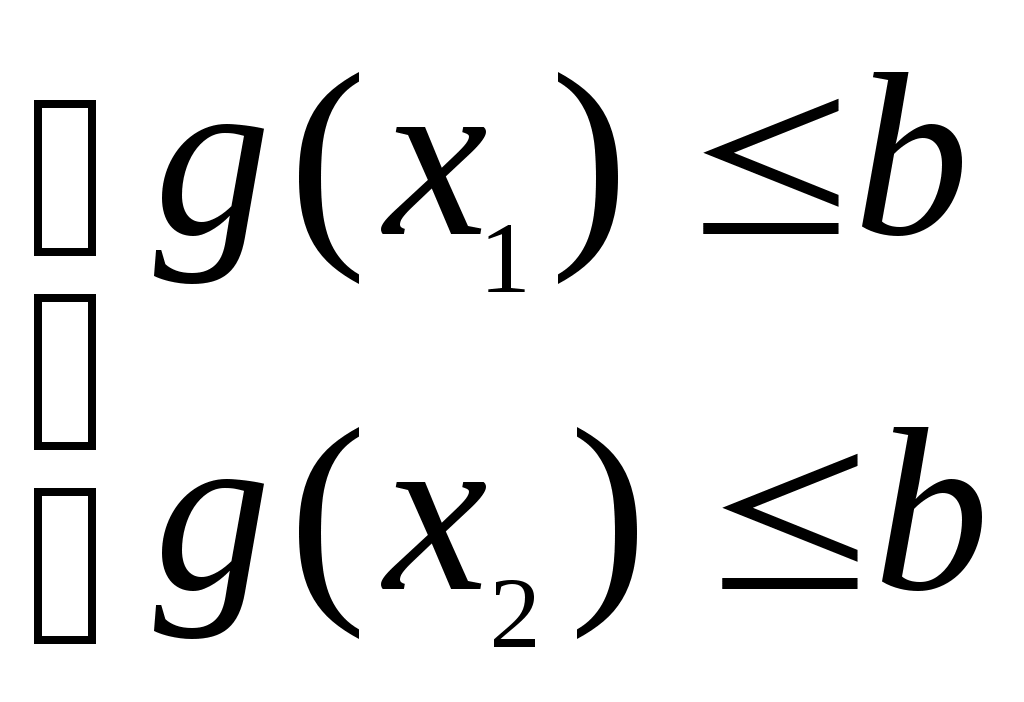)И  , тогда для любого 0 ≤ λ ≤ 1 выполняются условия:λg(x1) ≤ λb и (1 – λ)g(x2) ≤ (1 – λ)b , складывая, получим: λg(x1) + (1 – λ)g(x2) ≤ λb + (1 – λ)b = b и учитывая соотношения (3), получаем: ≤ b, ч.т.д.Известно, что пересечение выпуклых множеств выпукло. В связи с этим множество решений системы неравенств  – выпукло, если в неравенствах со знаком «≤» gi – выпуклые функции, а в неравенствах со знаком «≥» gi – вогнутые функции для x ≥ 0.Можно доказать, что выпуклая функция f(x), определенная на выпуклом множестве M непрерывна в любой внутренней точке этого множества. Теорема 2. Еслиf(x) – выпуклая функция, заданная на замкнутом выпуклом множестве  , тогда любой локальный минимум функции f(x) на множестве M является и глобальным.Докажем от противного. Предположим, что в точке  функция f(x) имеет локальный минимум, а в точке X*– глобальный минимум, причем:  . Так как f(x) – выпуклая функция, то для любого 0 ≤ λ ≤ 1 справедливо соотношение.  (4)Множество M выпукло, поэтому точка λX*+ (1 – λ) при0 < λ <1 принадлежит множеству M. Неравенство (4) можно усилить если вместо  представим  , будем иметь < (5)Значение λ можно выбрать так, чтобы точка λX*+ (1 – λ) была расположена как угодно близко к . Тогда из (5) получим, что в этой близкой к точке функция f принимает значение меньшее, чем в точке , а это противоречит тому, что точка является точкой локального минимума. Противоречие доказывает теорему.Следствие 1. Если глобальный минимум достигает в двух различных точках, то он достигается и в любой точке отрезка, соединяющего данные точки. Следствие 2. Если f(x) – строго выпуклая функция, то ее глобальный минимум на выпуклом множестве M достигается в единственной точке. Необходимое и достаточное условие выпуклости f(x). Пусть f(x) – непрерывная функция и имеет непрерывные частные производные первого порядка на выпуклом множестве M. Определение. Если функция f(X) дифференцируема в точке X0 , то градиентом f(X) в точке X0 называется n-мерный вектор: gradf(X0) =  Если функция f(x) непрерывна и дифференцируема во внутренних точках множества M и выпукла на нем, то можно получить следующий результат:  (6), где X1 и X2 – любые внутренние точки множества M. Это условие выполняется для любых внутренних точек X1 и X2 и является необходимым и достаточным условием выпуклости функции f(x). Если функцияfнепрерывна вместе с частными производными первого порядка и вогнута на множестве M, то  (7).Теорема 3. Выпуклая функция  , определенная на выпуклом множестве M достигает своего глобального минимума в каждой точке  , в которой gradf( ) = 0.Доказательство. Пусть в точке X*, gradf(X*) = 0. Пусть X – произвольная точка множества M, X*= X(1), а  = X(2), тогда из (6) получим 0 ≤ f( ) – f(X*) или gradf(X*)( –X*) или f( ) ≥ f(X*), ч.т.д.Таким образом, выпуклая функция f(x) достигает своего глобального минимума на множестве M в каждой точке, где  .* * * Можно показать, что если M – замкнутое, ограниченное сверху выпуклое множество, то глобальный максимум выпуклой функции f(x) достигается на нем в одной или нескольких угловых точках (при этом предполагается, что в точке X значение функции f(X) – конечно). Применяя при решении таких задач процедуру перебора крайних точек, можно получить точку локального максимума, но нельзя установить, является ли эта точка точкой глобального максимума. * * * Для вогнутых функций получим следующий результат. Пусть f(x) – вогнутая функция, заданная на замкнутом выпуклом множестве M  En . Тогда любой локальный максимум f(x) на множестве M является глобальным. Если глобальный максимум достигается в двух различных точках множества, то он достигается в любой точке отрезка, соединяющего эти точки.Для строго вогнутой функции существует единственная точка, в которой она достигает глобального максимума. Градиент вогнутой функции f(x) в точках максимума равен нулю, если f(x) – дифференциальная функция. * * * Глобальный минимум вогнутой функции, если он конечен, на замкнутом ограниченном снизу множестве должен достигаться в одной или нескольких его угловых точках, если функция f(x) конечна в каждой точке этого множества. |