Аксиомы стерометрии. Теорема Аксиомы стерометрии
 Скачать 165.18 Kb. Скачать 165.18 Kb.
|
|
Теорема: Аксиомы стерометрии Изучая математику, вы со многими понятиями знакомились с помощью определений. Так, из курса планиметрии вам хорошо известны определения четырёхугольника, трапеции, окружности и т. п. Определение любого понятия основано на других понятиях, содержание которых вам уже известно. Например, рассмотрим определение трапеции: «Трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие не параллельны». Видим, что определение трапеции основано на таких уже введённых понятиях, как четырёхугольник, сторона четырёхугольника, параллельные и непараллельные стороны и т. д. Итак, определения вводятся по принципу «новое основано на старом». Тогда ясно, что должны существовать первоначальные понятия, которым определений не дают. Их называют основными понятиями (рис. 1.1).  В изученном вами курсе планиметрии определения не давали таким фигурам, как точка и прямая. В стереометрии, помимо них, к основным понятиям отнесём ещё одну фигуру — плоскость. Наглядное представление о плоскости дают поверхность водоёма в безветренную погоду, поверхность зеркала, поверхность полированного стола, мысленно продолженные во всех направлениях. Используя понятие плоскости, можно считать, что в планиметрии мы рассматривали только одну плоскость, и все изучаемые фигуры принадлежали этой плоскости. В стереометрии же рассматривают бесконечно много плоскостей, расположенных в пространстве. Как правило, плоскости обозначают строчными греческими буквами 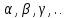 . На рисунках плоскости изображают в виде параллелограмма (рис. 1.2) или в виде других ограниченных частей плоскости (рис. 1.3). . На рисунках плоскости изображают в виде параллелограмма (рис. 1.2) или в виде других ограниченных частей плоскости (рис. 1.3). Плоскость, так же как и прямая, состоит из точек, т. е. плоскость — это множество точек. Существует несколько случаев взаимного расположения точек, прямых и плоскостей в пространстве. Приведём примеры. На рисунке 1.4 изображена точка A, принадлежащая плоскости 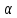 . Также говорят, что точка A лежит в плоскости . Также говорят, что точка A лежит в плоскости 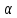 , или что плоскость , или что плоскость 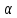 проходит через точку A. Коротко это можно записать так: проходит через точку A. Коротко это можно записать так:  . Приведённая запись означает, что точка А является элементом множества точек, представляющих собой плоскость . Приведённая запись означает, что точка А является элементом множества точек, представляющих собой плоскость 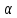 . . На рисунке 1.5 изображена точка B, не принадлежащая плоскости . Коротко это можно записать так: 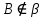 . . На рисунке 1.6 изображена прямая a, принадлежащая плоскости 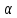 . Также говорят, что прямая a лежит в плоскости . Также говорят, что прямая a лежит в плоскости 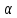 или что плоскость или что плоскость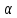 проходит через прямую a. Коротко это можно записать так: проходит через прямую a. Коротко это можно записать так: 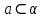 . Приведённая запись означает, что множество точек прямой a является подмножеством множества точек, представляющих собой плоскость . Приведённая запись означает, что множество точек прямой a является подмножеством множества точек, представляющих собой плоскость 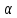 . .Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость. На рисунке 1.7 изображена прямая a, пересекающая плоскость 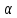 в точке A. Пишут: a ∩α =A . в точке A. Пишут: a ∩α =A .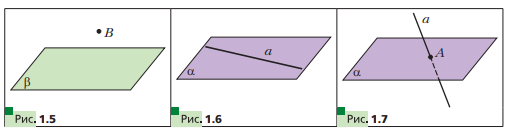 В дальнейшем, говоря «две точки», «три прямые», «две плоскости» и т. п., будем иметь в виду, что это разные точки, разные прямые и разные плоскости. Если две плоскости имеют общую точку, то говорят, что эти плоскости пересекаются. На рисунке 1.8 изображены пересекающиеся плоскостии α и β . Они пересекаются по прямой a. Пишут: α ∩β = a. На начальном этапе изучения стереометрии невозможно доказывать теоремы, опираясь на другие утверждения, поскольку этих утверждений ещё нет. Поэтому первые свойства, касающиеся точек, прямых и плоскостей в пространстве, принимают без доказательства. Как вы знаете из курса планиметрии, такого рода утверждения называют аксиомами. Отметим, что ряд аксиом стереометрии по формулировкам дословно совпадают со знакомыми вам аксиомами планиметрии. Например: • какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей; • через любые две точки можно провести прямую, и притом только одну. Аксиома 1. Для любой плоскости пространства существует точка, ей не принадлежащая Аксиома 2. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. Аксиома 3. Если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости. В этом случае говорят, что прямая лежит в плоскости или что плоскость проходит через прямую. Из аксиомы 2 следует, что прямая, не лежащая в плоскости, не может иметь с плоскостью более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость. 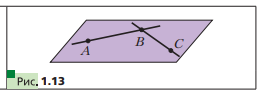 Аксиома 4. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей. В этом случае говорят, что плоскости пересекаются по прямой. Эту аксиому можно проиллюстрировать с помощью согнутого листа бумаги или с помощью вашего учебника (рис. 1.15). 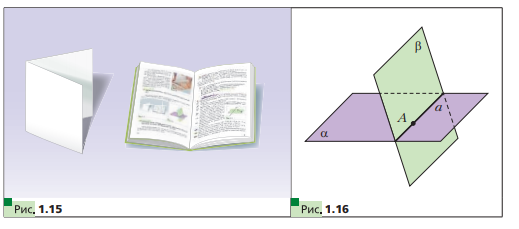 Аксиома 5. В любой плоскости пространства выполняются все аксиомы планиметрии. Таким образом, в любой плоскости пространства можно использовать все доказанные теоремы и формулы из планиметрии. Аксиома 6. Расстояние между любыми двумя точками пространства одинаково для любой плоскости, проходящей через эти точки. Некоторые следствия из аксиом Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна. Следствие 2. Через две пересекающиеся прямые проходит плоскость и притом только одна. Следствие 3. Через две параллельные прямые проходит плоскость и притом только одна.  Домашнее задание: Перепишите лекцию и ответьте на вопросы  |
