статика. 1 Лекции статика. Теоретическая механика
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
Теоретическая механика Теоретическая механика – есть наука об общих законах механического движения и взаимодействия материальных тел. Теоретическая механика является базой для всех технических дисциплин. По характеру рассматриваемых задач она подразделяется на статику, кинематику и динамику. 1. Статика Статикой называется раздел теоретической механики, в котором излагается общее учение о силах, и изучаются условия равновесия тел, находящихся под действием сил. Основные определенияАбсолютно твердое тело – это такое тело, расстояние между двумя любыми точками которого всегда остается постоянным. Сила – есть количественная мера механического взаимодействия тел. Сила – величина векторная, она определяется тремя параметрами: линией действия, направлением вдоль линии и величиной (модулем). Сила – это скользящий вектор, который можно перемещать вдоль линии действия. П 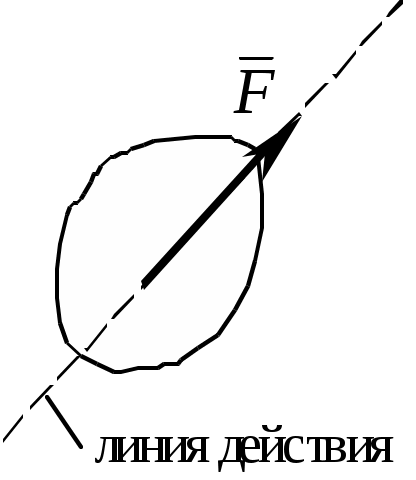 рямая, вдоль которой направлена сила, называется линией действия силы. рямая, вдоль которой направлена сила, называется линией действия силы.Вся совокупность сил, действующих на твердое тело, называется системой сил. Равнодействующая сила – это такая сила, которая заменяет действие системы сил на твердое тело (сила эквивалентна системе). Уравновешенной называется система сил, под действием которой тело находится в состоянии равновесия. Под состоянием равновесия в механике понимают состояние покоя или равномерного и прямолинейного движения. Сила равная по модулю равнодействующей, противоположно ей направленная вдоль той же линии действия называется уравновешивающей силой. Аксиомы статикиВсе теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без доказательств и называемых аксиомами или принципами статики. Аксиома 1. Если тело находится в равновесии под действием двух сил, то эти силы имеют общую линию действия, противоположны по направлению и равны по величине.  Аксиома 2. Действие системы сил на тело не изменится, если к этой системе добавить или от нее отнять уравновешенную систему сил. 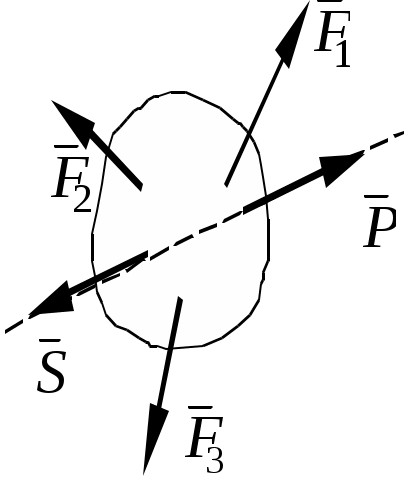 С  ледствие (из аксиом 1 и 2): Действие силы на абсолютно твердое тело не изменится, если силу перенести в любую точку тела по линии действия. ледствие (из аксиом 1 и 2): Действие силы на абсолютно твердое тело не изменится, если силу перенести в любую точку тела по линии действия.Пусть есть сила F в точке A. В точку B на линии действия силы F помещаем уравновешенную систему сил F1 и F2, так чтобы Аксиома 3. Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах как на сторонах.  , ,Пользуясь аксиомой 3 можно не только складывать любое количество сил, но и раскладывать на любое число направлений. А 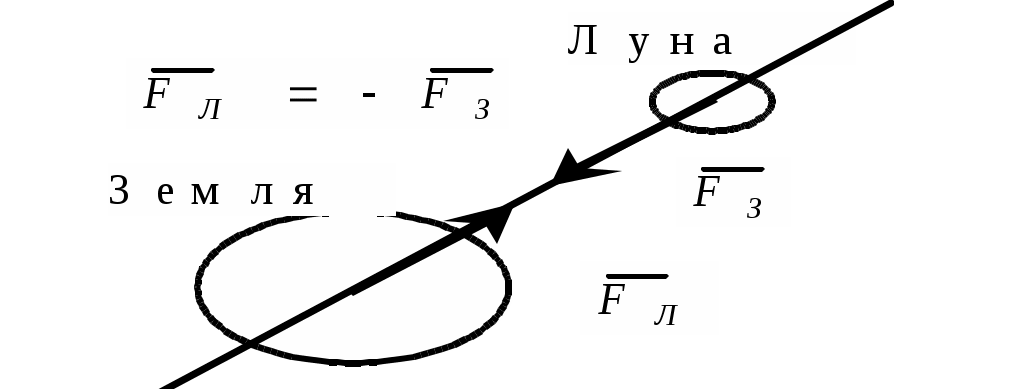  ксиома 4. Всякому действию одного тела на другое существует равное по величине, но противоположное по направлению противодействие. ксиома 4. Всякому действию одного тела на другое существует равное по величине, но противоположное по направлению противодействие.Силы, возникающие при взаимодействии, не образуют уравновешенную систему, так как приложены к разным телам.Аксиома 5. Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать мгновенно отвердевшим (абсолютно твердым).Аналитическое задание и сложение силСилы можно задавать и складывать аналитически с помощью их проекций на оси координат. П 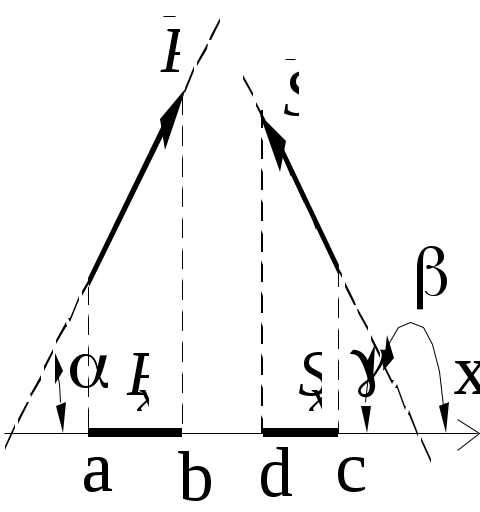 роекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца вектора силы. Проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси. Пусть сила F задана через свои проекции на координатные оси Fx, Fy, Fz. По приведенному выше определению проекции определяются выражениями 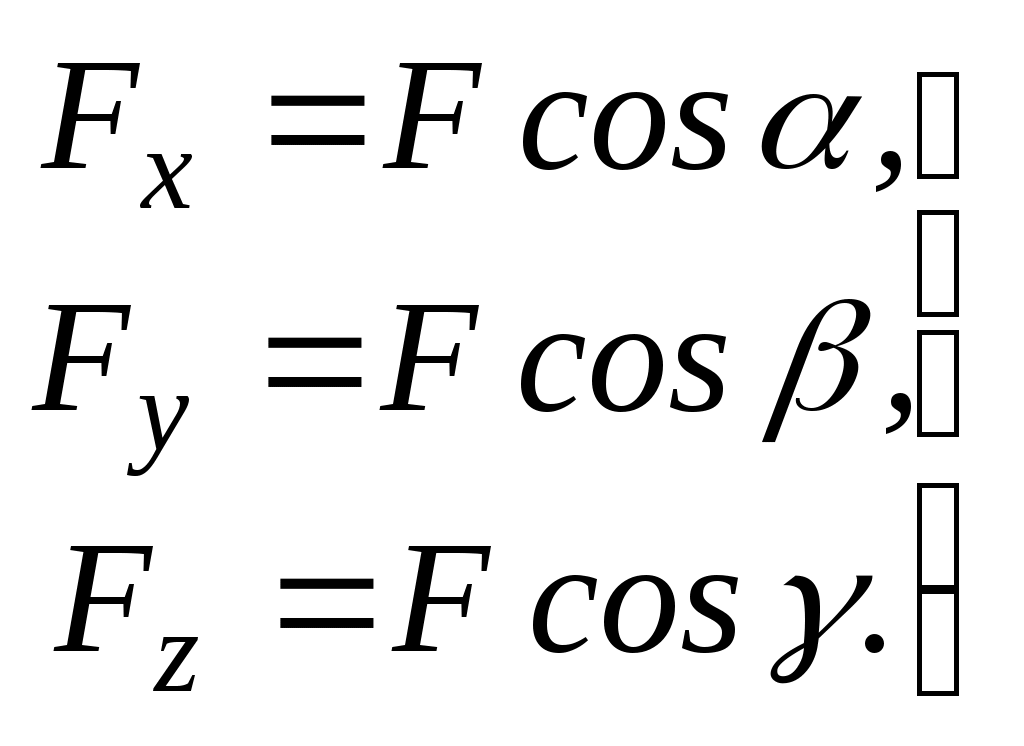 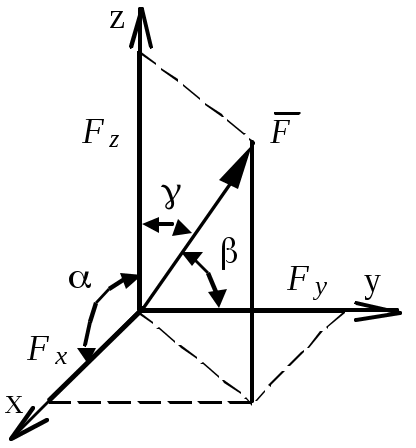 (1.4) (1.4)Углы в (1.4) удовлетворяют уравнению Возводя в квадрат (1.4) и складывая, с учетом (1.5) получим модуль силы и направляющие косинусы Направляющие косинусы указывают положение вектора силы в пространстве по отношению к координатным осям. Зная проекции сил на координатные оси, их можно складывать аналитически. Проекция вектора суммы на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось Модуль равнодействующей и направляющие косинусы определяются по (1.6) и (1.7) Связи и реакции связейТело, не связанное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным. Тело, перемещениям которого в пространстве препятствуют какие-либо другие тела, называется несвободным. Связями будем называть все тела, которые ограничивают перемещение данного тела. Сила, с которой данная связь действует на тело, называется реакцией связи. Направлена реакция связи всегда в сторону, противоположную той, куда связь не дает перемещаться телу. Типы связей1. Гладкая поверхность.  Реакция гладкой поверхности перпендикулярна этой поверхности. 2. Невесомый стержень. 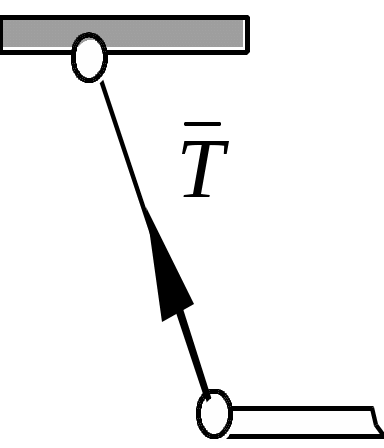 Реакция стержня всегда направлена вдоль его оси. Стержень может работать и на сжатие и на растяжение. 3. Неподвижный цилиндрический шарнир. К 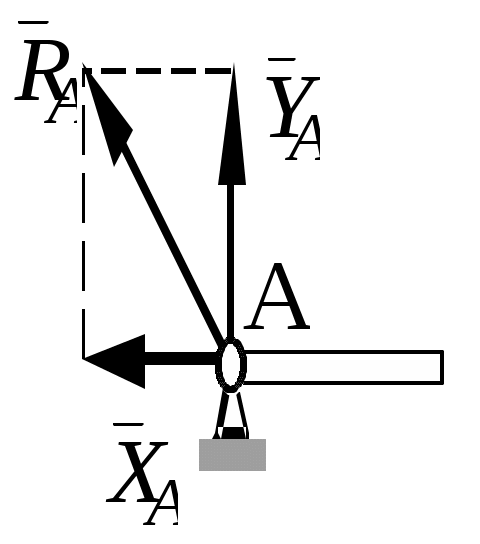 ак правило, направление реакции RA заранее не известно, поэтому ее раскладывают по двум известным направлениям, например, по направлению координатных осей. ак правило, направление реакции RA заранее не известно, поэтому ее раскладывают по двум известным направлениям, например, по направлению координатных осей.4. Подвижный цилиндрический шарнир. 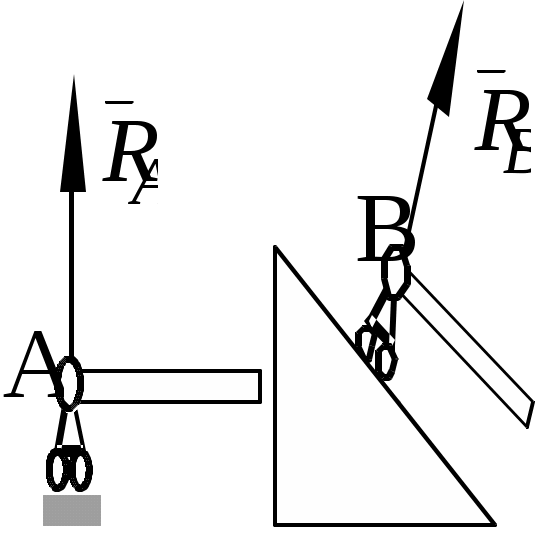 Реакция перпендикулярна плоскости возможного перемещения шарнира. 5 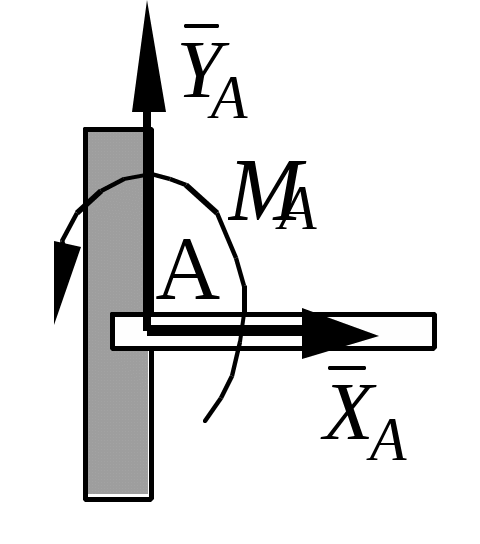 . Жесткая заделка. . Жесткая заделка.Реакция в данном случае состоит из трех компонентов: двух составляющих силы XA, YA и реактивного момента M неизвестного направления (понятие момента силы будет рассмотрено позже). 6. Скользящая заделка. Р 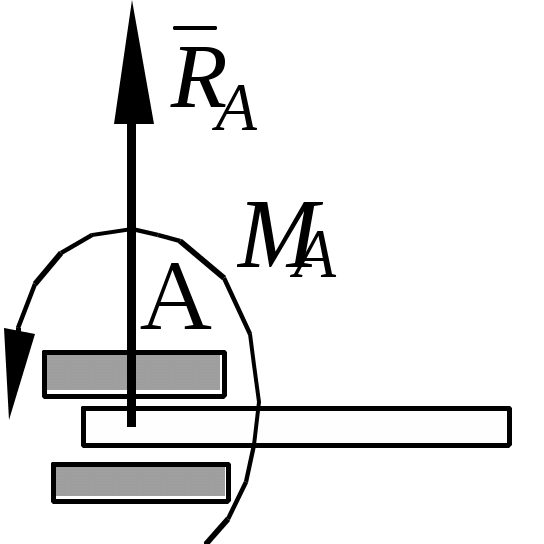 еакция включает силу, перпендикулярную оси заделки, и реактивный момент. еакция включает силу, перпендикулярную оси заделки, и реактивный момент.Система сходящихся сил Если линии действия сил пересекаются в одной точке, то такая система называется сходящейся системой сил. Эту систему можно заменить равнодействующей, построив силовой многоугольник или вычислив ее аналитически по выражениям (1.8)-(1.10). Условие равновесия сходящейся системы сил1. В геометрической форме. Для равновесия сходящейся системы сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым. 2. В аналитической форме. Для равновесия сходящейся системы сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из координатных осей были равны нулю При решении задач на равновесие сходящейся системы сил иногда удобно пользоваться следующей теоремой о трех силах. Теорема: Если тело находится в равновесии под действием трех сил, расположенных в одной плоскости, то линии действия этих сил параллельны или пересекаются в одной точке. Произвольная плоская система силМомент силы относительно точки (центра) Момент силы относительно точки это количественная характеристика вращательного эффекта от действия силы. Моментом силы относительно точки называется величина, равная взятому с соответствующим знаком произведению модуля силы на плечо, т.е. кратчайшее расстояние от центра до линии действия силы 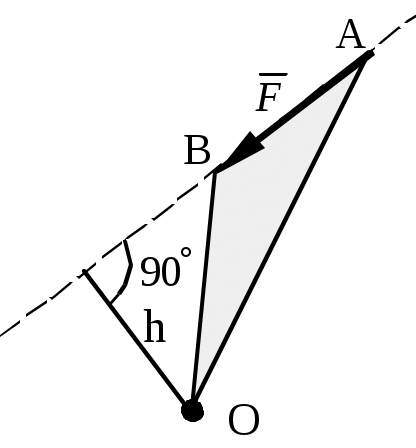 . (1.13) . (1.13)Если сила стремится повернуть тело относительно точки против часовой стрелки, то момент положительный, если по часовой стрелке – отрицательный. Момент силы относительно центра равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через этот центр. Момент силы численно выражается удвоенной площадью OAB При решении задач для вычисления момента силы в некоторых случаях удобно пользоваться следующей теоремой Вариньона о моменте равнодействующей. Теорема: Момент равнодействующей плоской сходящейся системы сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра. Сложение параллельных силНайдем равнодействующую двух действующих на твердое тело параллельных сил в двух случаях: 1. Силы направлены в одну сторону. Равнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в одну сторону, равна по модулю сумме модулей слагаемых сил, им параллельна и направлена в туже сторону. Линия действия равнодействующей проходит между точками приложения слагаемых сил на расстояниях от этих точек, обратно пропорциональных этим силам. 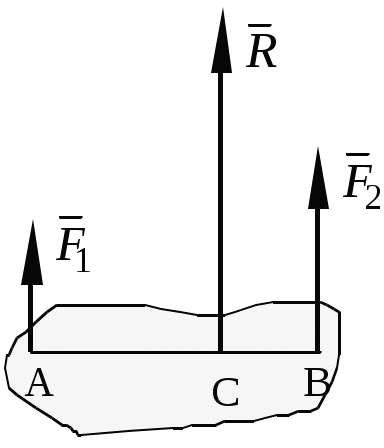 , , 2. Силы направлены в разные стороны. Р 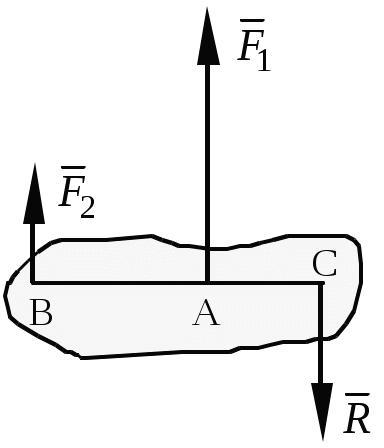 авнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в разные стороны, равна по модулю разности модулей слагаемых сил, им параллельна и направлена в сторону большей силы. Линия действия равнодействующей проходит вне отрезка, соединяющего точки приложения слагаемых сил, на расстояниях от этих точек, обратно пропорциональных силам. авнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в разные стороны, равна по модулю разности модулей слагаемых сил, им параллельна и направлена в сторону большей силы. Линия действия равнодействующей проходит вне отрезка, соединяющего точки приложения слагаемых сил, на расстояниях от этих точек, обратно пропорциональных силам.С помощью приведенных формул можно решать задачи и о разложении силы на две ей параллельные. Пара силПара сил - это система двух равных по модулю, параллельных и направленных в противоположные стороны сил. Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары. Расстояние между линиями действия сил пары называется плечом пары. П 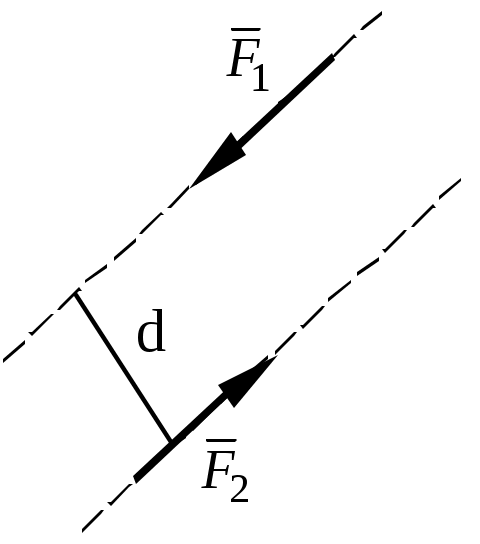 ара сил не имеет равнодействующей. Действие пары на тело сводится к некоторому вращательному эффекту, численно характеризуемому моментом пары сил. ара сил не имеет равнодействующей. Действие пары на тело сводится к некоторому вращательному эффекту, численно характеризуемому моментом пары сил.Моментом пары сил называется величина, равная взятому с соответствующим знаком произведению модуля одной из силы пары на ее плечо Свойства пары сил 1. Действие пары сил на тело не изменится, если у нее произвольным образом изменить силы и плечо при неизменном моменте пары. 2. Не изменяя действия пары сил, ее можно переносить произвольным образом в плоскости ее действия. 3. Пару сил можно повернуть в плоскости ее действия на любой угол. 4. Действие нескольких пар сил, приложенных в одной плоскости, можно заменить одной парой сил, момент которой равен алгебраической сумме моментов заданных пар сил. Условие равновесия плоской системы сил Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на оси координат и алгебраическая сумма моментов всех сил относительно любой точки равнялись нулю Теорема о параллельном переносе силыТеорема: Силу, приложенную к твердому телу, можно, не изменяя оказываемого действия, переносить параллельно ей самой в любую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится.  Приведение плоской системы сил к заданному центруПользуясь теоремой о параллельном переносе, систему сил, действующую на твердое тело, можно перенести в одну точку. Эту точку будем называть центром приведения. При этом сила Теорема: Всякая плоская система сил, при приведении к произвольному центру O заменяется одной силой R, равной главному вектору системы, и приложенной в центре приведения, и одной парой с моментом MO, равным главному моменту системы относительно центра O. Пространственная система силЧтобы перейти к рассмотрению системы сил, расположенных в пространстве, необходимо уточнить и расширить введенные ранее понятия. Момент силы относительно центра как векторМомент силы относительно центра можно изобразить в виде вектора, который приложен в центре O, равен по модулю произведению силы на плечо и перпендикулярен к плоскости, проходящей через центр O и силу F. Направлен вектор в ту сторону, откуда поворот, совершаемый силой, виден происходящим против хода часовой стрелки. М 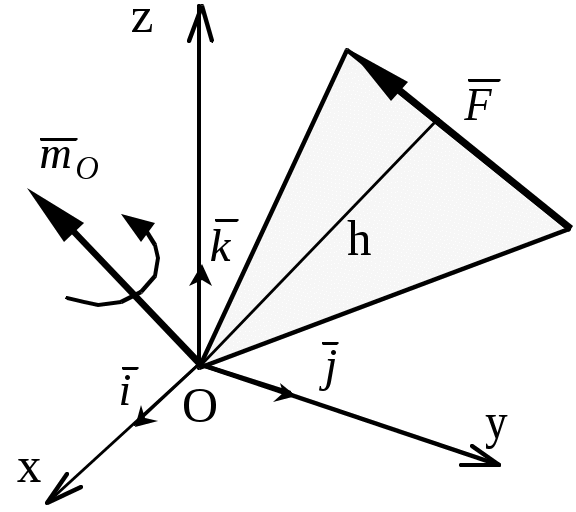 омент силы относительно центра можно вычислить аналитически. Для этого через центр O нужно провести координатные оси. Допустим, что известны координаты точки приложения вектора F и его проекции на оси Fx, Fy, Fz,, тогда, проекции вектора-момента на оси вычисляются по формулам омент силы относительно центра можно вычислить аналитически. Для этого через центр O нужно провести координатные оси. Допустим, что известны координаты точки приложения вектора F и его проекции на оси Fx, Fy, Fz,, тогда, проекции вектора-момента на оси вычисляются по формуламМодуль вектора и направляющие косинусы где i, j, k – единичные векторы координатных осей. Момент пары сил как векторВ 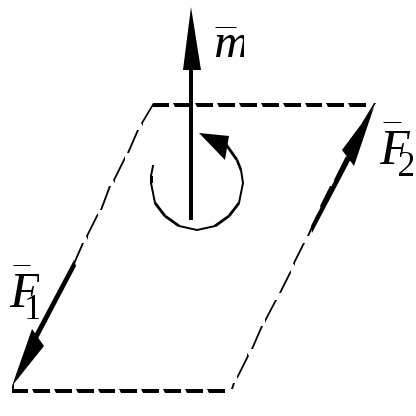 ектор-момент пары сил равен по модулю моменту пары, т.е. произведению одной из сил на плечо, и направлен перпендикулярно плоскости действия пары в ту сторону, откуда поворот пары виден происходящим против хода часовой стрелки. ектор-момент пары сил равен по модулю моменту пары, т.е. произведению одной из сил на плечо, и направлен перпендикулярно плоскости действия пары в ту сторону, откуда поворот пары виден происходящим против хода часовой стрелки.Момент силы относительно осиМомент силы относительно оси характеризует вращательный эффект, создаваемый силой, стремящейся повернуть тело вокруг данной оси. Пусть на твердое тело, которое может вращаться относительно некоторой оси z, действует сила F, приложенная в точке A. Проведем через точку A плоскость xy, перпендикулярную оси z, и разложим силу F на составляющие: Fz, параллельную оси z, и Fxy, лежащую в плоскости xy. Сила Fz параллельна оси и не может повернуть тело относительно нее. Весь вращательной эффект от силы F будет совпадать с вращательным эффектом ее составляющей Fxy. Отсюда получим, что М 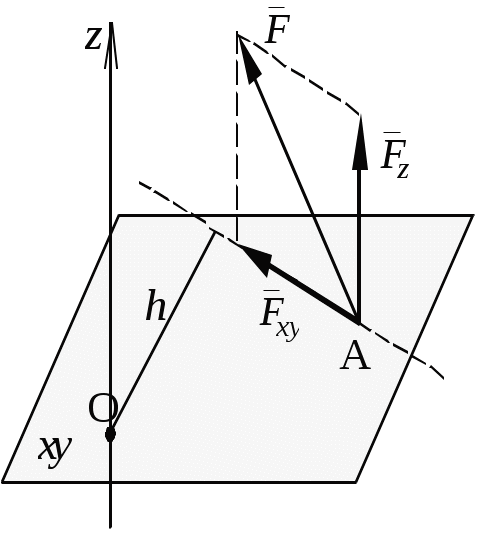 оментом силы относительно оси называется алгебраическая величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью. оментом силы относительно оси называется алгебраическая величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.Момент считается положительным, если с положительного конца оси z поворот, который стремится совершить сила Fxy, виден происходящим против часовой стрелки, и отрицательным, если по часовой стрелке (например, на рисунке момент положительный). Чтобы найти момент силы относительно оси надо: провести плоскость xy, перпендикулярную к оси z (в любом месте); спроектировать силу F на эту плоскость и вычислить величину Fxy; опустить из точки O пересечения оси с плоскостью перпендикуляр на линию действия силы Fxy и найти плечо h; вычислить момент Fxyh и найти его знак. Момент силы относительно оси равен нулю, если сила параллельна оси (Fxy=0), или если линия действия силы пересекает ось (h=0). Условие равновесия пространственной системы силДля равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю. 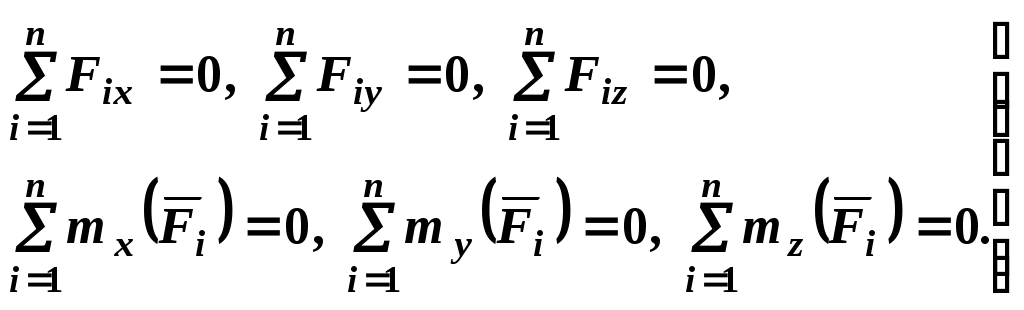 (1.23) (1.23) |
