статистика оборотных средств. Статистика оборотных средств курсовая. Теоретические основы формирования оборотных средств предприятия
 Скачать 487.22 Kb.
|
2.3. Корреляционно-регрессионный анализ взаимосвязи признаковВ завершении работы проведем корреляционно-регрессионный анализ зависимости прибыли от продаж от коэффициента оборачиваемости оборотных активов. Данные для анализа представим в таблице 9. Таблица 9 Данные для корреляционно-регрессионного анализа зависимости прибыли от продаж и стоимости оборотных средств ООО «Сармаш»
Построим корреляционное поле (рис.6). 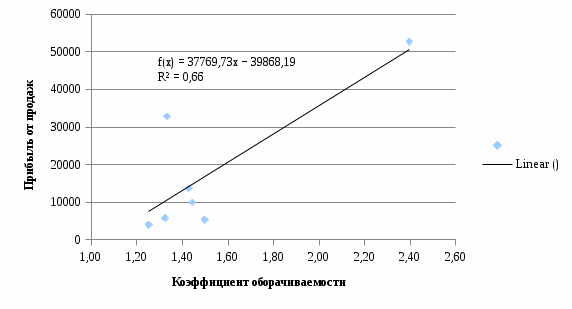 Рис. 6. Корреляционное поле  Для наших данных система уравнений имеет вид 7a + 10,68·b = 124161 10,68·a + 17,21·b = 224431,03 Домножим первое уравнение системы на -1,525.  -10,68a - 16,28·b = -189367,35 10,68·a + 17,21·b = 224431,03 0,93·b=35063,69 Получаем коэффициенты регрессии: b = 37769,7, a = -39868,2 Уравнение регрессии: y = -39868,2 x + 37769,7 Выборочные средние. 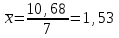 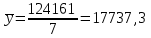 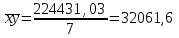 Выборочные дисперсии: 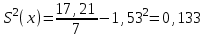 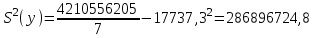 Среднеквадратическое отклонение 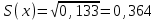 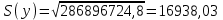 Рассчитываем показатель тесноты связи. 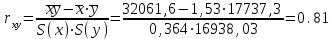 Линейный коэффициент корреляции принимает значения от –1 до +1. Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока: 0.7 < rxy < 0.9: высокая; В нашем случае связь между коэффициентом оборачиваемости оборотных средств и прибылью от продаж прямая и высокая. 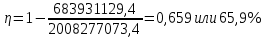 т.е. в 65,9% случаев изменения коэффициента оборачиваемости оборотных средств приводят к изменению прибыли от продаж. Остальные 34,1% изменения прибыли от продаж объясняются факторами, не учтенными в модели (а также ошибками спецификации). Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму: 1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α. 2. Далее определяют фактическое значение F-критерия: 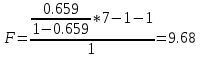  3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2. Fтабл - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости α. Уровень значимости α - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно α принимается равной 0,05 или 0,01. 4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу. В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом. Табличное значение критерия со степенями свободы k1=1 и k2=5, Fтабл = 6.61. Поскольку фактическое значение F>Fтабл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна). Проиллюстрируем алгоритм расчета с помощью программы Excel (рис.7).  Рис. 7. Расчет параметров уравнения регрессии с помощью программы Excel Таким образом, проведенный корреляционно-регрессионный анализ зависимости прибыли от продаж показал, что связь между названными показателями прямая и тесная. В 65,9% случаев изменения коэффициента оборачиваемости оборотных средств приводят к изменению прибыли от продаж. Остальные 34,1% изменения прибыли от продаж объясняются факторами, не учтенными в модели (а также ошибками спецификации). Коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна). |