курсовая. ОГЛАВЛЕНИЕ. Теоретические подходы к изучению функции в школе сущность понятия функции и графика
 Скачать 65.89 Kb.
|
|
ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ ПОДХОДЫ К ИЗУЧЕНИЮ ФУНКЦИИ В ШКОЛЕ Сущность понятия: функции и графика Функциональная (или функционально-графическая) линия ‒ основной стержень, который проходит от арифметики до высших разделов единой математики, и вокруг него группируется вся современная школьная алгебра, начала анализа и в некоторой мере геометрия. Существующая примерная программа содержит значительно увеличенный объем сведений функционального содержания после проведенной в 70-е гг. ХХ в. реформы математического образования. Расширение понятийного аппарата вплоть до включения начал математического анализа подняло функциональные представления учащихся на новый качественный уровень. Существенное влияние на такой решительный шаг оказали идеи педагогов-математиков Ф. Клейна, А. Я. Хинчина, А. Н. Колмогорова, А. И. Маркушевича, А. Г. Мордковича и других, убежденных в ведущей роли понятия функции в математике-науке и в обучении математике, непосредственно связанного с реальной действительностью. В нем ярко воплощены изменчивость и динамичность реального мира, причинно-следственная связь и обусловленность реальных объектов и явлений, диалектические черты современного математического мышления. Функция, являющаяся математической моделью многих реальных ситуаций, позволяет описывать и изучать разнообразные зависимости между величинами, познавать окружающий мир. Поэтому так важно знакомить учащихся с функциональным материалом, который позволяет осуществлять как внутрипредметные, так и межпредметные связи (многие понятия и законы носят функциональную основу), реализовывать прикладную направленность школьной математики. Понятие функции в математике складывалось постепенно, возникая из самых разнообразных задач практики, когда находили общие приемы их решения (абстрагируясь от конкретного содержания задачи). Исходным пунктом здесь было понятие переменной величины. Содержание понятия функции развивалось, обогащалось в процессе эволюции математики, существовало множество споров относительно вновь вводимых определений. И сейчас невозможно сказать, что математика нашла окончательное, последнее определение понятия. Понятие функции прошло долгий путь развития и имеет свою историю. Хотя идея функциональной зависимости величин относится к глубокой древности, потребность в общем понятии функции возникла лишь в XVII в. в связи с возникновением идеи переменных, с которой в математику вошло движение, изменение, процессы, наблюдаемые во времени. Первоначальная трактовка была либо геометрической, либо механической: ординаты точек совершенно произвольных кривых – функции от абсцисс, путь и скорость – функции от времени (П. Ферма, Р. Декарт, И. Ньютон, Г. Лейбниц). В этот период Г. Лейбниц ввел термины: «функция» (1673), «переменная», «константа» (1698). Термин «функция» в переводе с латинского означает «свершение», «выполнение». Постепенно трактовка функции стала освобождаться от первоначальных представлений и доминировать стала аналитическая – отождествляющая функцию с формулой, задающей ее (И. Бернулли, Л. Эйлер). И. Бернулли в 1718 г. дал впервые явное определение функции, Л. Эйлер в 1734 г. ввел обозначение y = f(x). Примерно в середине XIX в. понятие функции освободилось от единовластия формулы, и в новом определении делается акцент на идею соответствия (Н. И. Лобачевский, Л. Дирихле), которое называют классическим, близким к современным. После создания общей теории множеств идея соответствия была дополнена идеей множества, позволившей рассматривать функцию не только для числовых множеств, но и на объектах произвольной природы. В конце XIX в. сформировалось понятие отображения, развивающее понятие функции. В ХХ в. в связи с потребностями физики возникли «обобщенные функции» (Л. Шварц, С. Л. Соболев), сильно отличающиеся по внешнему виду от исходных представлений о функции. На примере развития понятия функции возможно познакомить учащихся с проявлением важных философских категорий – причины и следствия. С понятием функции связана определенная система общефункциональных понятий (числовая функция, области определения и значений, способы задания, график, возрастание и убывание, четность и нечетность, нули (корни) функции, знакопостоянство, монотонность, экстремумы, периодичность, обратная и сложная функции, непрерывность или разрывность, приращение аргумента и функции, дифференцируемость, интегрируемость и др.). Многие из перечисленных понятий именуются и свойством функции, и названием отдельного вида функций. Например, свойство периодичности одной из тригонометрических функций указывает одновременно на принадлежность ее к виду периодических функций, выделяемых данным свойством. Важное место в функциональной линии уделяется глубокому изучению класса функций, получивших название элементарных (не значит простых), которые имеют широкую область применения. К элементарным функциям, которые уже к XVII в. были хорошо изучены, относят многочлены, рациональные и иррациональные функции, показательную, логарифмическую, тригонометрические и обратно тригонометрические функции. Этот набор функций тесно связан с основными арифметическими операциями (сложение, вычитание, умножение, деление), алгебраическими операциями (возведение в целую степень, извлечение корня) и трансцендентными операциями (возведение в иррациональную степень, логарифмирование, тригонометрическими, модуль), понятием непрерывности и геометрическими преобразованиями, что позволяет устанавливать связи функциональной линии с другими содержательно-методическими линиями. Классификацию элементарных функций можно представить в следующем виде: 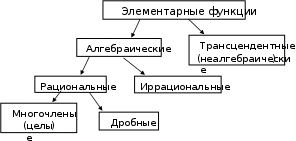 Приведенная классификация относит ту или иную функцию к определенному виду по «внешнему признаку», т. е. в зависимости от проводимых операций. Однако не всякая функция, заданная формулой, содержащей трансцендентные операции, является трансцендентной. Так, например, функция  не трансцендентная, т. к. ее закон соответствия может быть выражен посредством алгебраических операций: y = 2 + x2. Слово «трансцендентный» произошло от латинского transendens перешагивающий, выходящий за пределы чего-либо. Трансцендентные функции выходят за пределы алгебраических. К классу элементарных функций относят и различные их комбинации, получаемые путем использования арифметических операций. Однако в школьном курсе определения таких операций с функциями отсутствуют. Арифметические операции с числовыми функциями все же неявно прослеживаются (при построении графиков, в некоторых формулировках, например, производная суммы и т. п.). Основные элементарные функции могут соединяться между собой и с помощью операции взятия (отыскания) функции от функции. В таком случае мы придем к понятию сложной функции или композиции функций. Пусть даны две функции y = f(z) и z = g(x), тогда функцию y = f(g(x)) называют композицией двух данных функций или сложной функцией, составленной из них. Функция z = g(x) называется промежуточным аргументом, x – основным аргументом. Композиция функций  результат последовательного применения этих функций в определенном порядке. Для записи композиции функций часто употребляется значок «о» и пишут h = f0g, т. е. функция h получена как композиция функций f и g (сначала применяется g, а затем f). Ясно, что если z есть функция от x, а y есть функция от z, то y можно рассматривать как сложную функцию от x. Например, функцию  можно рассматривать как композицию функций z = 1 – x2 и y  . Такое задание сложной функции называют еще цепным заданием. При этом цепь функций может состоять из любого их числа. Из функций z  образовать сложную функцию нельзя, т. е.  в области действительных чисел не существует, т. к. никакому числу x не соответствует число y. Поэтому при рассмотрении сложных функций следует иметь в виду области определения составляющих функций. С понятием функции тесно связано понятие обратной функции и умение выяснять, имеет ли данная функция обратную, и если имеет, то как ее найти. Слово «обратный» часто используется в математике: обратное число, обратная дробь, обратное действие, обратная теорема, взаимно обратные числа (теоремы), взаимно обратные отношения (2:3 и 3:2) и др. Какой смысл вкладывается в понятие «обратная функция»? В учебнике М. И. Башмакова (9-й класс) дается такое определение: «Обратной функцией для функции f называется такая функция g, которая каждому числу y (из области значений функции f) ставит в соответствие такое число x, для которого f(x) = y». Если функция y = f(x) имеет обратную (иногда ее обозначают x = f--1(y)), то f(x) называют обратимой, а функции y = f(x) и x = f-1(y) – взаимно обрат- ными. Например, пары функций y = kx и x  взаимно обратные. В ныне действующих учебниках алгебры приводятся примеры кусочных функций, т. е. функций, заданных различными формулами на разных промежутках области определения. Графики таких функций составляются из отдельных «кусочков» известных учащимся функций, создавая целостный образ, что и послужило основанием для их названия. Во многих случаях именно кусочные функции считаются математическими моделями реальных ситуаций. Такие функции стали рассматриваться только в середине XIX в., когда и было уточнено определение функции. Некоторые из них имеют свои названия и обозначения: модуль (│x│), знак (sign x), целая часть ([x]), дробная часть ({x}), функция Дирихле (D(x)). Функции такого рода не являются элементарными. Последний важный вопрос, относящийся к теории: что такое равные функции? Пусть даны две функции y = f(x) и y = g(x), они будут равными, если имеют одну и ту же область определения и для любого x = a из их области определения f(a) = g(a). Такие функции еще называют тождественными, одинаковыми. Основные свойства функций Роль и место функций в школьном курсе математики ГЛАВА 2. МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ПРИМЕНЕНИЕ СВОЙСТВ ФУНКЦИИ ПРИ РЕШЕНИИ ЗАДАЧ ШКОЛЬНОГО КУРСА МАТЕМАТИКИ 2.1. Элементарная функция как средство решения уравнений. 2.2. Использование свойств монотонных функций при решении неравенств ЗАКЛЮЧЕНИЕ СПИСОК ЛИТЕРАТУРЫ |