Теоретические положения Деревья. Основные понятия
 Скачать 452 Kb. Скачать 452 Kb.
|
Рис. 3. Представление дерева в виде списков дочерних узловНа рис. 3 в виде совокупности связных списков представлено дерево, показанное на рис. 2. Здесь используется массив указателей-заголовков, индексированных номерами узлов. Любой заголовок узла i указывает на связный список элементов, являющихся дочерними узлами данного узла, расположенных в порядке слева направо. Аналогичное дерево можно построить без использования указателей, с помощью двух массивов структур. В одном из них хранятся ключи с соответствующими заголовками, имеющими произвольное местоположение. В другом – цепочки дочерних узлов для каждого заголовка ( рис. 4). Например, узел E дерева, изображенного на рис. 4, имеет три дочерних узла (G, H, I) с индексами в первой таблице 1, 3, 9 соответственно. Заголовок, соответствующий ключу E, из первой таблицы содержит индекс 8 второй таблицы. В первом поле структуры с этим номером хранится индекс 1 ключа G, второе поле содержит индекс (в той же таблице), соответствующий структуре, содержащей индекс следующего ключа (дочернего узла) из первой таблицы и т.д. 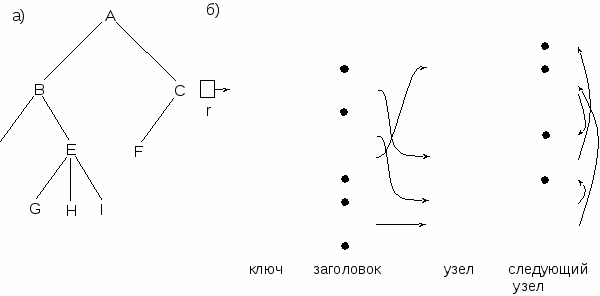
Рис. 4. Представление дерева в виде списка дочерних узлов, не использующее указатели: а – исходное дерево, б – массивы для его хранения Можно упростить структуру дерева, если все элементы хранить в одном массиве (списке) структур. Каждая из них будет содержать ключ, индекс (ссылку на) самый левый дочерний узел, индекс (ссылку на) узел непосредственно правого соседа (рис. 5).
Рис. 5. Представление дерева в виде списка дочерних узлов с использованием одного массива структур Представление деревьев с помощью указателей Классический способ представления деревьев предполагает наличие совокупности структур, каждая из которых в простом случае содержит ключ и указатели на аналогичные структуры, количество которых равно степени дерева: struct Tree { Tree *leftmost_child; Tree *right_sibling_1; Tree *right_sibling_2; ... Tree *right_sibling_k; //для дерева степени k+1 }; 1.3. АВЛ-деревья Оптимальным для хранения в памяти является дерево, у которого на каж-дом уровне размещается максимально возможное число узлов. Такое дерево на-зывается сбалансированным. Двоичное дерево называется идеально сбалансированным, если число вершин в его левых и правых поддеревьях отличается не более чем на единицу. Поддержание идеальной сбалансированности требует слишком больших накладных расходов. Советскими математиками Адельсоном-Вельским и Ландисом предложено менее строгое определение сбалансированности деревьев: двоичное дерево называется сбалансированным в том и только в том случае, когда высоты двух поддеревьев каждой из вершин дерева отличаются не более, чем на единицу. Такие деревья стали называть АВЛ-деревьями [2, 3]. Рассмотрим аспекты балансировки АВЛ-дерева при выполнении операций включения и исключения ключей. Пусть рассматриваемое дерево состоит из корневой вершины r и левого (L) и правого (R) поддеревьев. Обозначим через hl высоту L, а через hr - высоту R. Пусть выполняется операция включения, и новый ключ включается в поддерево L. Если высота L не изменяется, то не изменяются и соотношения между высотами L и R, и свойства АВЛ-дерева сохраняются. Если же при включении в поддерево L высота этого поддерева увеличивается на единицу, то возможны следующие три случая: • если hl = hr, то после добавления вершины поддеревья L и R станут разной высоты, но свойство сбалансированности сохранится; • если hl < hr, то после добавления новой вершины L и R станут равной высоты, т.е. сбалансированность общего дерева улучшится; • если hl > hr, то после включения ключа критерий сбалансированности нарушится и потребуется перестройка дерева. Существует лишь два случая, каждый из которых требует индивидуального подхода к балансировке (рис. 6, а, б). Результаты балансировок показаны на рис. 6, в, г. (переходы от несбалансированных схем деревьев к соответствующим сбалансированным показаны стрелками). Примеры балансировок после включения узлов приведены на рис. 7. При исключении вершин из АВЛ-дерева также возможна его балансировка. Удаление терминальных вершин и вершин с одним потомком тривиально, вершину с двумя потомками заменяют на самую правую (левую) вершину его левого (правого) поддерева. Балансировка, возможно, потребуется, если уменьшилась высота дерева [3]. 1.4. В-деревья Механизм классических B-деревьев был предложен в 1972 г. Байером и Мак-Крейтом с целью организации эффективного внешнего поиска. B-дерево порядка m представляет собой сильноветвящееся дерево, удовлетворяющее следующим условиям [5]: 1. Каждый узел имеет не более m потомков. 2. Каждый узел, за исключением корня и листьев, имеет не менее m/2 потомков (через m/2 обозначено округление вправо, т.е. взятие наименьшего целого числа, которое не меньше m/2). 3. Корень, если он не является листом, имеет минимум двух потомков. 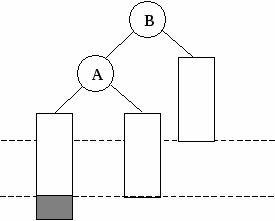 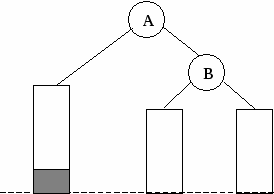  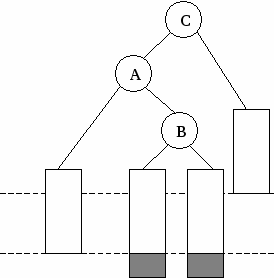 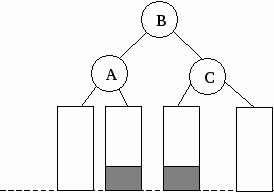 а в а в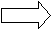 б г Рис. 6. Несбалансированность после включения – а, б; итоги балансировки – в, г 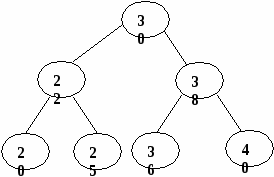 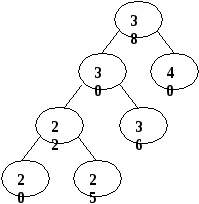 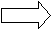    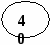 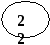 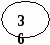    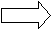 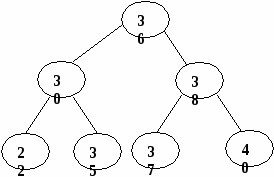   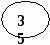 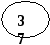 Рис. 7. Примеры балансировки АВЛ-деревьев после включения узлов 4. Все листья находятся на одном уровне и не содержат информации. 5. Нелистовой узел с k потомками содержит k-1 ключей. На рис. 8 показан пример B-дерева порядка 5. Узлы В-дерева называются страницами. Они содержат ключи и ссылки на другие страницы. Ключи в каждом узле расположены в порядке возрастания слева направо с использованием естественного обобщения концепции симметричного порядка, количество листьев на единицу больше количества ключей. Так как листья являются «пустыми», ссылки из предшествующих листьям страниц можно сделать ни на что не указывающими. 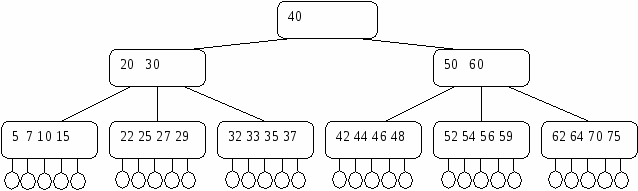 Рис. 8. B-дерево порядка 5 Поиск в B-дереве прямолинеен. Рассмотрим поиск заданного ключа k. В основную память считывается корневая страница B-дерева. Предположим, что она содержит ключи k1, k2, ..., kn и ссылки на страницы p0, p1, ..., pn. В ней последовательно (или с помощью какого-либо другого метода поиска в основной памяти) ищется ключ k. Если он обнаруживается, поиск завершен. Иначе возможны три ситуации:
Для внутренних страниц поиск продолжается аналогичным образом, пока либо не будет найден ключ k, либо не будет достигнута листовая страница (обнаружена необходимость перехода по ссылке, которая ни на что не указывает). Если достигнута листовая страница, ключ k в B-дереве отсутствует. Чтобы вставить новый ключ k в B-дерево порядка m, в котором все листья расположены на уровне l, необходимо вставить новый ключ в подходящее место на уровне l-1. Можно осуществить поиск ключа k описанным выше способом и дойти до нужной страницы А, предшествующей листовой. Далее возможны два случая. Если страница А содержит менее m ссылок на потомков, ключ k помещается на свое место, определяемое порядком сортировки ключей в странице. Если же данная страница уже заполнена, то необходимо разбить страницу А на две страницы. При этом создается новая страница C. Ключи из страницы A и ключ k поровну распределяются между A и C, а средний ключ вместе со ссылкой на страницу C переносится в непосредственно родительскую для А страницу B (рис. 9). Такое деление может повлечь деление страницы B и т.д. до корня, который также может быть разделен. В последнем случае будет создан новый корень (высота дерева увеличится на единицу), в который переместится средний ключ из совокупности ключей предыдущей корневой страницы и ключа k. При исключении различают два случая – удаление ключа из страницы, непосредственно предшествующей листовой, и удаление ключа из внутренней страницы. В первом случае удаляемый ключ убирается из списка ключей. Во втором случае для сохранения корректной структуры B-дерева удаляемый ключ необходимо заменить минимальным (максимальным) ключом страницы, предшествующей листовой, достигнутой при переходе от страницы с удаляемым ключом вначале по самой правой (левой), а затем по всем самым левым (правым) ссылкам. В любом из указанных случаев может возникнуть ситуация, в которой одна из страниц после удаления будут содержать меньшее, чем требуется, количество ключей. Поэтому если в некоторой странице А количество ключей оказалось меньшим, чем m/2-1, необходимо осуществить процедуру перераспределения ключей или слияния. Для этого берется одна из соседних (в частности, с максимальным количеством ключей) листовых страниц – страница В (у страниц А и В имеется общая страница-предок); если на странице B имеется не менее m/2 ключей, возможно перераспределение. При этом ключи, содержащиеся в страницах А и В, а также средний ключ страницы-предка поровну распределяются между ними, и новый средний ключ заменяет тот, который был заимствован у страницы-предка. 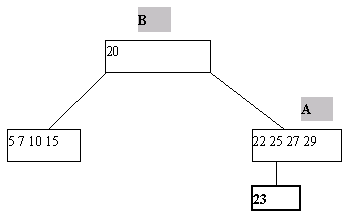 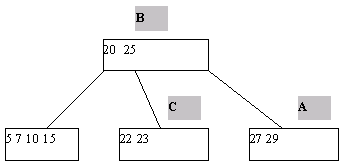 а б Рис. 9. Пример включения в B-дерево (листья не показаны): а – попытка вставить ключ 23 в заполненную страницу; б – выполнение включения ключа 23 Если количество ключей на странице В равно минимально возможному – m/2-1, следует выполнить процедуру слияния страниц А и В. При этом к ключам страниц А и В добавляется средний ключ из страницы-предка (из страницы-предка он изымается), эти ключи формируют содержимое страницы, полученной слиянием страниц А и В. Поскольку в странице-предке число ключей уменьшилось на единицу, может оказаться, что число элементов в ней стало меньше m/2-1, тогда на этом уровне выполняется процедура перераспределения, а возможно, и слияния. Так может продолжаться до внутренних страниц, находящихся непосредственно под корнем B-дерева. При необходимости слияния страниц, общим предком которых является корень, содержащий единственный ключ, высота дерева уменьшится на единицу. Пример удаления ключа из В-дерева порядка 5 со слиянием показан на рис. 10. 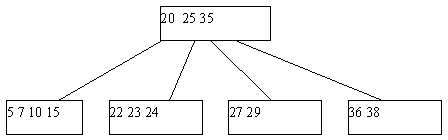  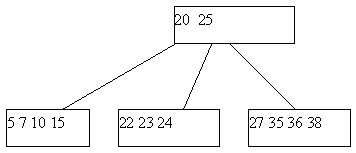 Рис. 10. Пример удаления ключа 29 из B-дерева 1.5. Алгоритмы на графах С формальной точки зрения граф представляет собой упорядоченную пару G = (V, E) множеств, первое из которых состоит из вершин или узлов графа, а второе – из его ребер. Ребро связывает между собой две примыкающие друг к другу (соседние) вершины и часто обозначается этой парой вершин. Графы бывают ориентированными (орграфами) и неориентированными. В орграфе ребро представляет собой упорядоченную пару вершин – начало и конец, в неориентированном графе – неупорядоченную пару вершин, его концов. Путь в графе или орграфе – последовательность ребер, по которым можно поочередно проходить. Во взвешенном графе каждому ребру приписано число, называемое весом ребра. Граф называется связным, если всякую пару узлов можно соединить по крайней мере одним путем. Цикл – это путь, который начинается и заканчивается в одной и той же вершине. Более подробно с терминологией можно ознакомиться в [4]. При работе с графами часто приходится выполнять некоторое действие по одному разу с каждой вершиной графа. Подобный обход может быть выполнен двумя способами – в глубину или по уровням. В обоих случаях одна из вершин графа выбирается в качестве отправной точки. Обход в глубину При обходе в глубину посещается первый узел, а затем происходит перемещение вдоль ребер графа до тех пор, пока не встретится тупик. Узел неориентированного графа является тупиком, если все примыкающие к нему узлы уже были посещены. В орграфе тупиком также называется узел, из которого нет выходящих ребер. После попадания в тупик необходимо передвигаться назад вдоль пройденного пути до тех пор, пока не будет обнаружена вершина, у которой есть еще не посещенный сосед, и затем двигаться в этом новом направлении. Процесс оказывается завершенным, когда произошел возврат в отправную точку и все примыкающие к ней вершины уже были посещены. Обход по уровням При обходе по уровням после посещения первого узла посещаются все соседние с ним вершины. При втором проходе посещаются все вершины, находящиеся на расстоянии двух ребер от начальной. При каждом новом проходе обходятся все вершины, расстояние от которых до начальной на единицу больше предыдущего. Для предупреждения повторного посещения необходимо либо вести список посещенных вершин, либо хранить информацию о посещении в соответствующей структуре данных узла. Алгоритмы поиска минимального остовного дерева Минимальным остовным деревом (МОД) связного взвешенного графа называется его связный подграф, состоящий из всех вершин исходного графа и некоторых его ребер, причем сумма весов ребер является минимально возможной. Такое дерево может понадобиться, например, для организации компьютерной сети. Дейкстра и Прим предложили так называемый «жадный» алгоритм построения МОД. «Жадные» алгоритмы действуют, используя в каждый момент часть исходных данных и принимая лучшее решение на основе этой части. В рассматриваемом случае на каждом шаге имеется множество ребер, которые могут быть присоединены к уже построенной части остовного дерева, из них выбирается ребро с наименьшим весом. Вершины графа разбиваются на три класса: вершины, вошедшие в уже построенную часть дерева, вершины, окаймляющие построенную часть, и еще не рассмотренные вершины. Алгоритм начинает работу с произвольной вершины графа, которая включается в остовное дерево. Все вершины, соединенные (соседние) с данной, заносятся в кайму. Затем выполняется цикл поиска ребра с наименьшим весом, соединяющего уже построенную часть остовного дерева с каймой; это ребро вместе с новой вершиной добавляется в дерево и происходит обновление каймы таким образом, чтобы список ребер из дерева в кайму включал ребра с наименьшими весами. После того, как в дерево попадут все вершины, работа будет закончена. Другой алгоритм построения МОД предложил Крускал. Алгоритм начинает работу с пустого дерева. К нему добавляются ребра в порядке возрастания их весов до тех пор, пока не будет получен набор ребер, объединяющий все вершины графа. В процессе выполнения необходимо не допускать добавление ребер, приводящих к появлению цикла в создаваемом дереве. Если ребра закончатся до того, как все вершины будут соединены между собой, это означает, что граф был несвязным, и полученный результат представляет собой объединение МОД всех его компонент связности [4]. 2. Задания к лабораторному практикуму 2.1. Лабораторная работа №1 «Программирование алгоритмов реализации и обработки древовидных структур неспециального вида» Цель работы Получение навыков реализации и использования деревьев неспециального вида, анализ эффективности работы с ними. |

