7. Кратные интегралы. Теоретические вопросы
 Скачать 1.36 Mb. Скачать 1.36 Mb.
|
|
VII. КРАТНЫЕ ИНТЕГРАЛЫ Теоретические вопросыОпределение двойного и тройного интегралов. Их геометрический и физический смысл. Основные свойства двойных и тройных интегралов. Теорема о среднем для двойного и тройного интегралов. Вычисление двойных интегралов двумя последовательными интегрированиями (случай прямоугольной области). Вычисление двойных интегралов двумя последовательными интегрированиями (общий случай). Замена переменных в двойном интеграле. Якобиан, его геометрический смысл. Двойной интеграл в полярных координатах. Тройной интеграл в цилиндрических координатах. Тройной интеграл в сферических координатах. Теоретические упражнения Пользуясь определением двойного интеграла, доказать, что 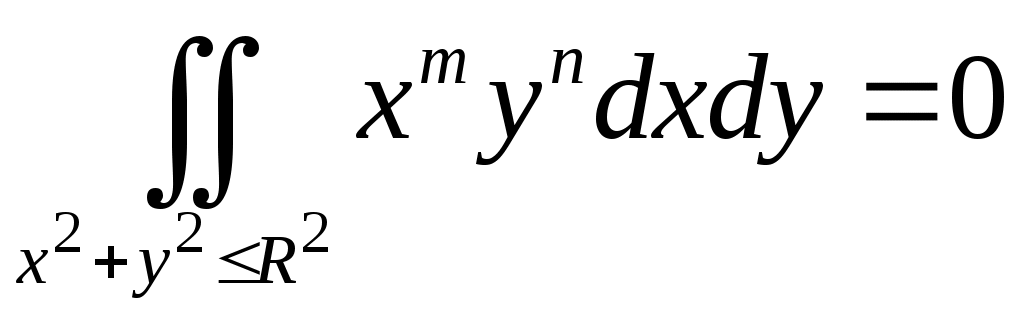 , ,если 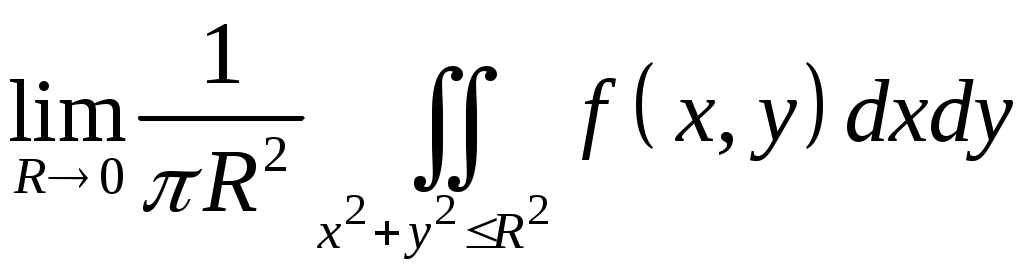 , ,где Оценить интеграл 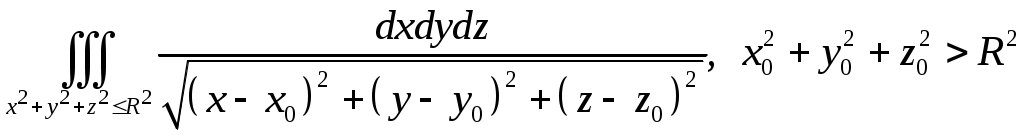 , ,т.е. указать, между какими значениями заключена его величина. Вычислить двойной интеграл 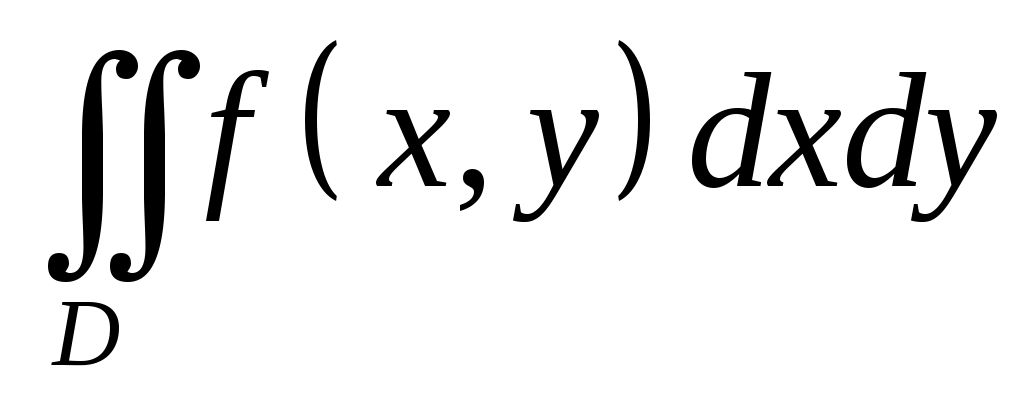 , ,если область Доказать равенство 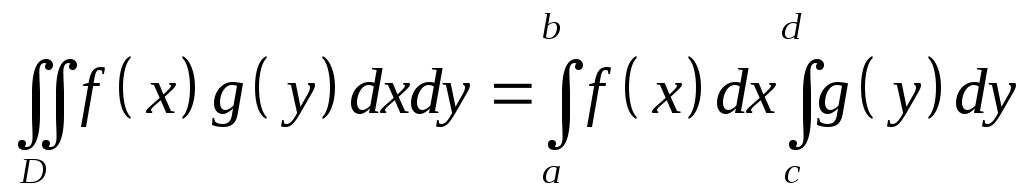 б бесли область Доказать формулу Дирихле 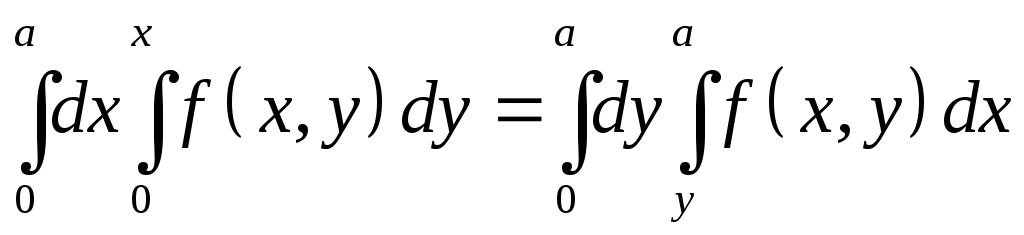 , , Пользуясь формулой Дирихле, доказать равенство 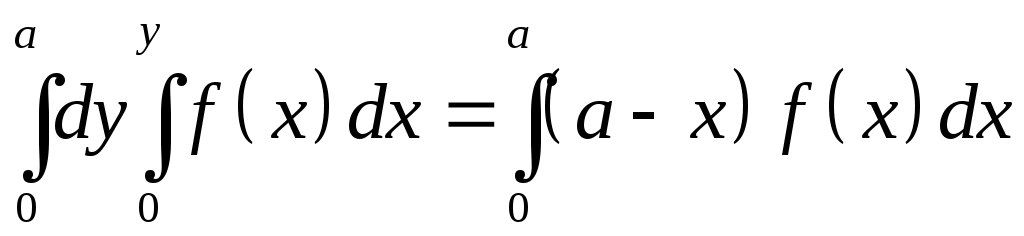 . .Какой из интегралов больше 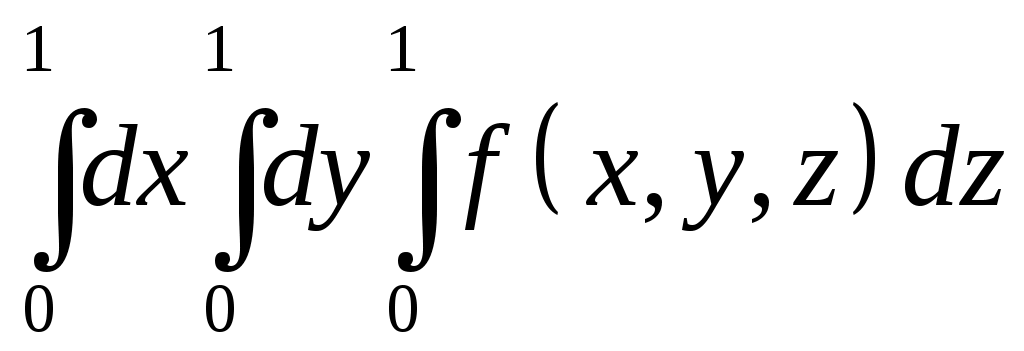 или или 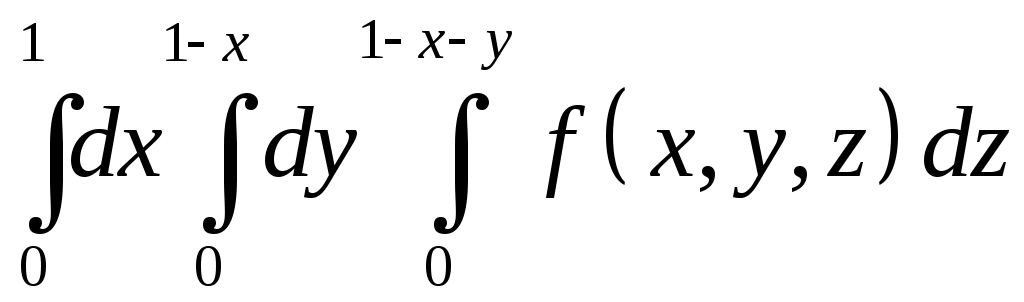 , ,если Расчетные заданияЗадача 1. Изменить порядок интегрирования. 1.1. 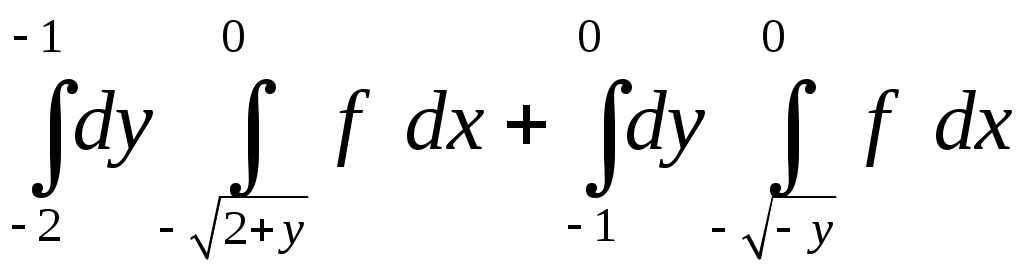 . 1.2. . 1.2. 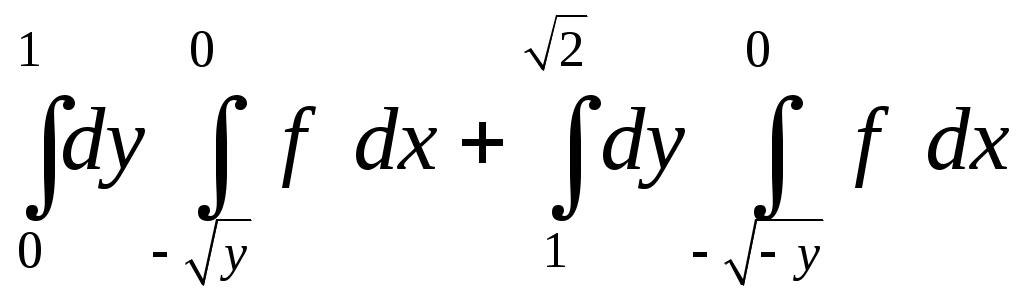 . .1.3. 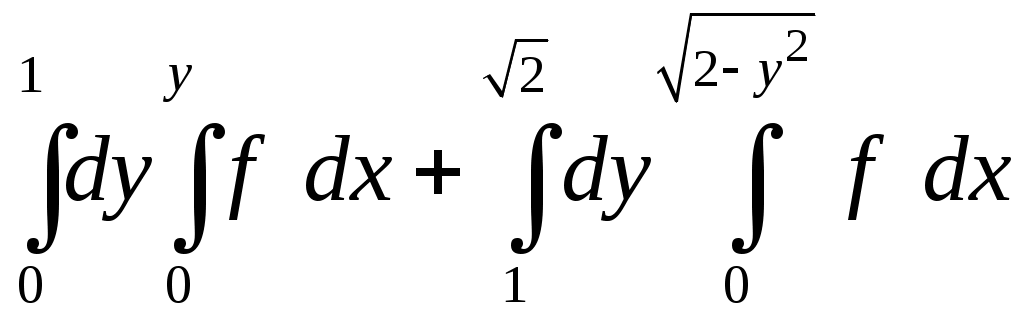 . 1.4. . 1.4. 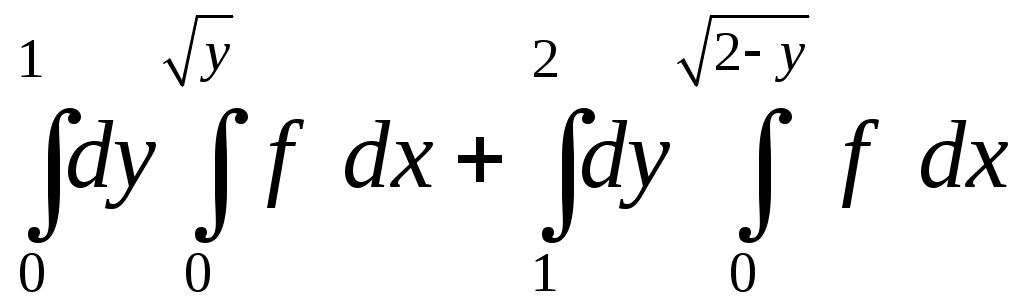 . .1.5. 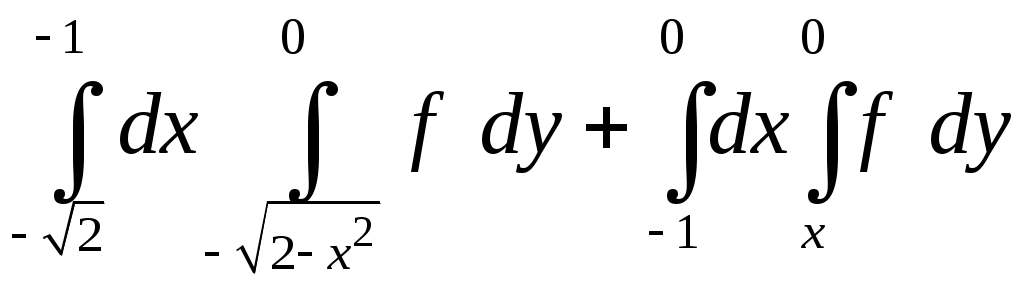 . 1.6. . 1.6. 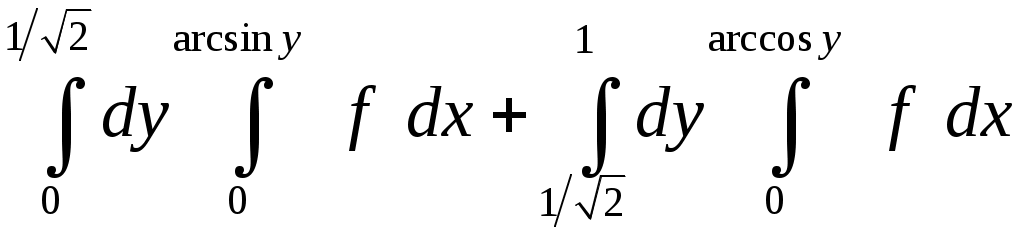 . .1.7. 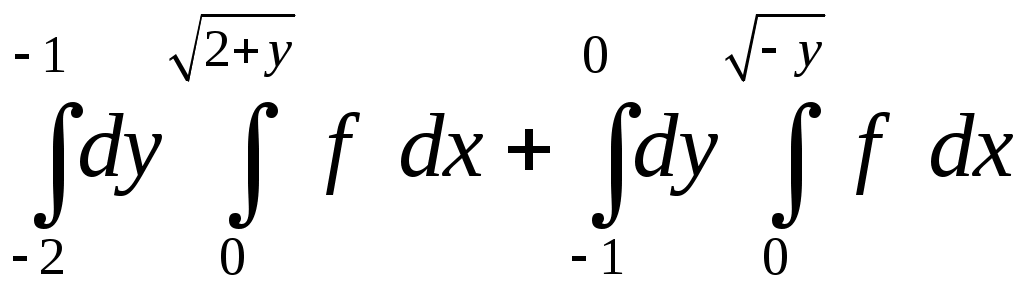 . 1.8. . 1.8. 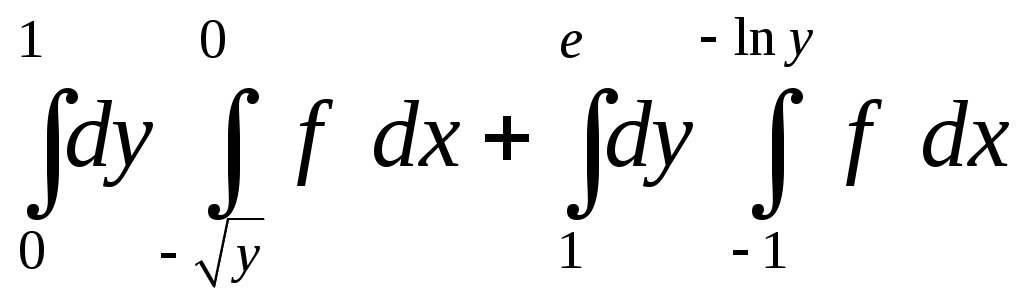 . .1.9. 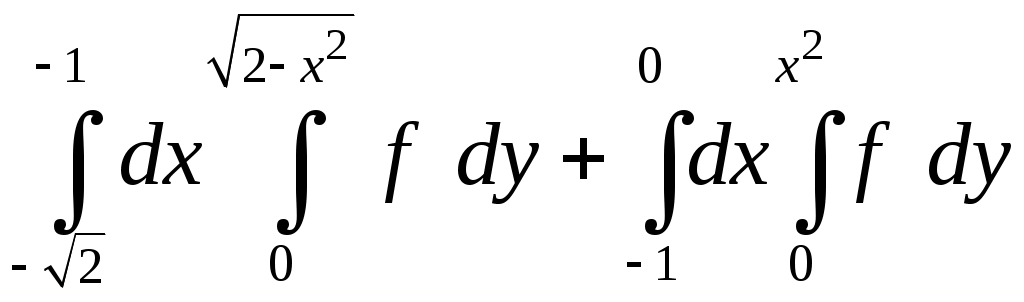 . 1.10. . 1.10. 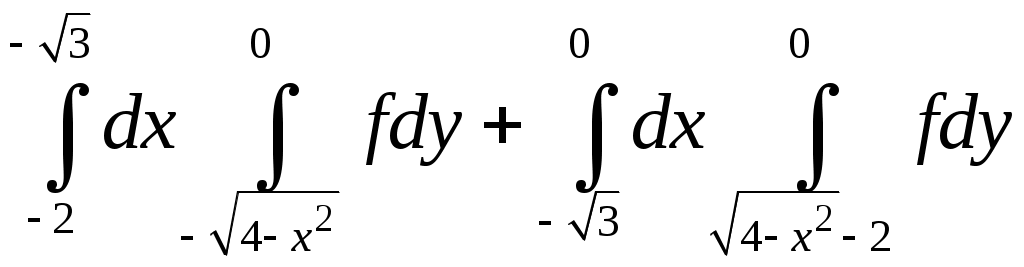 . .1.11. 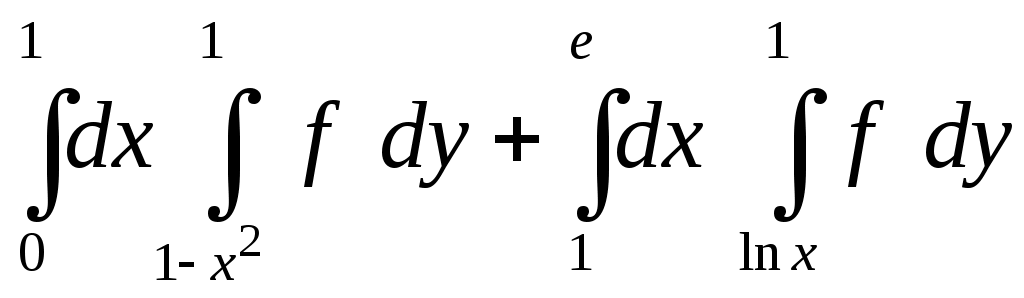 . 1.12. . 1.12. 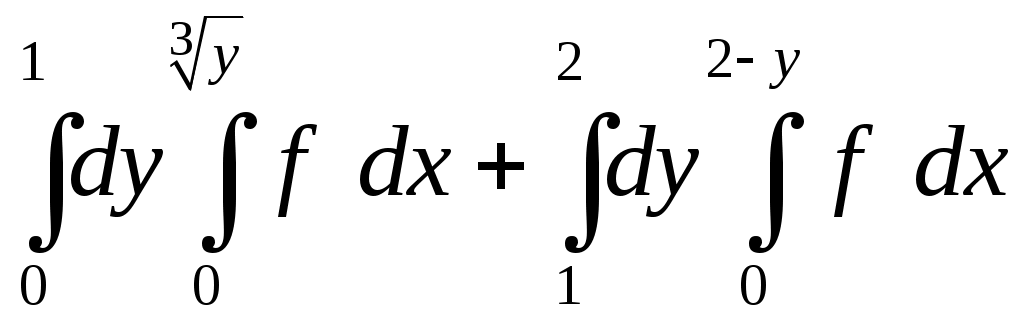 . .1.13. 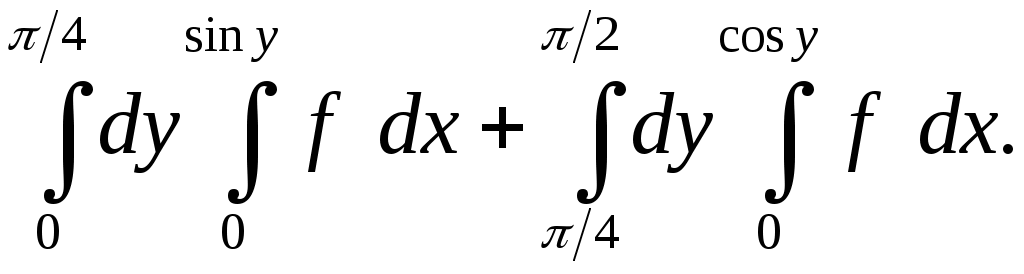 . 1.14. . 1.14. 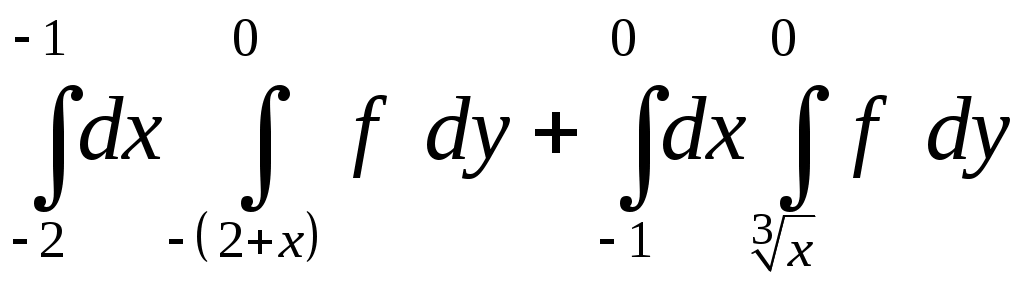 . .1.15. 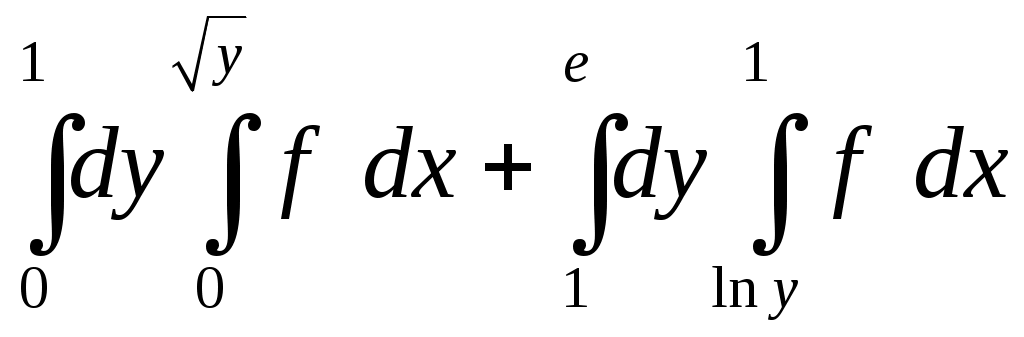 . 1.16. . 1.16. 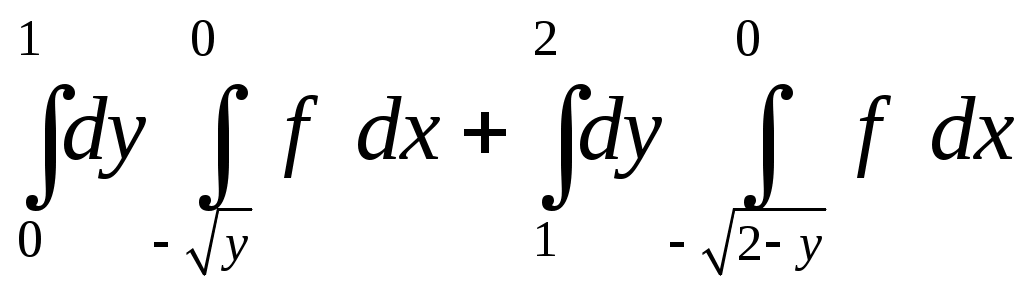 . .1.17. 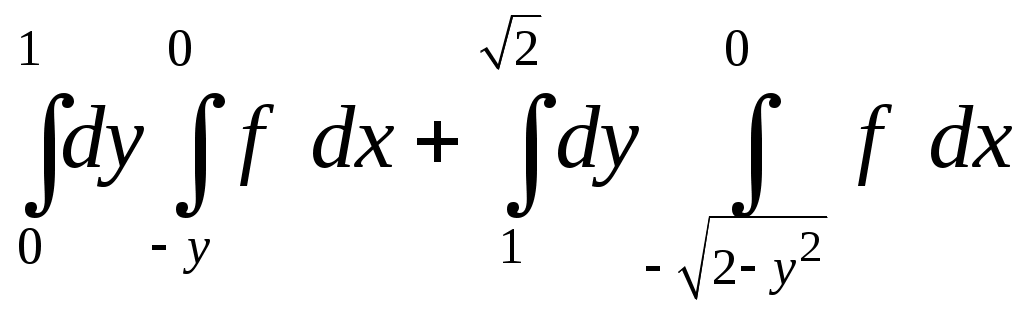 . 1.18. . 1.18. 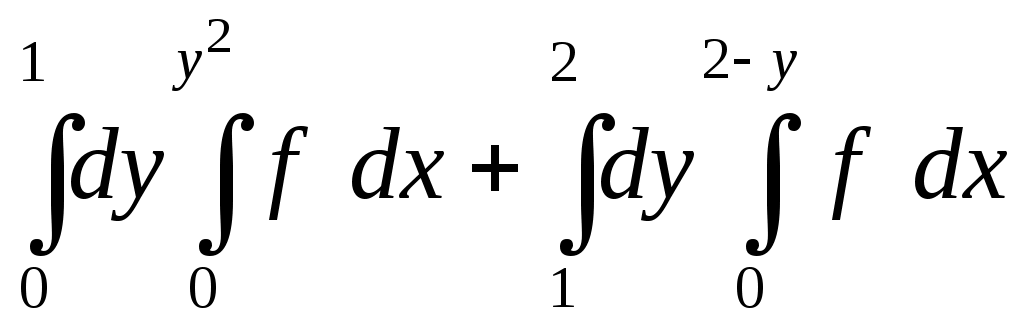 . .1.19. 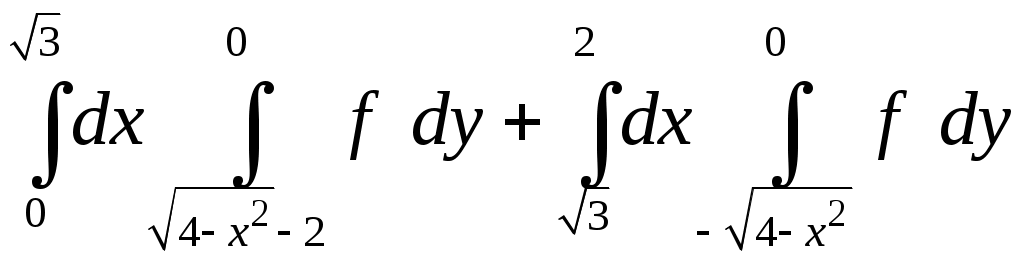 . 1.20. . 1.20. 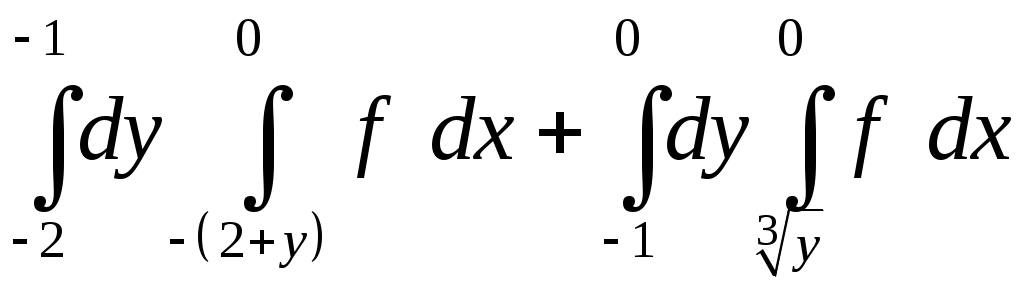 . .1.21. 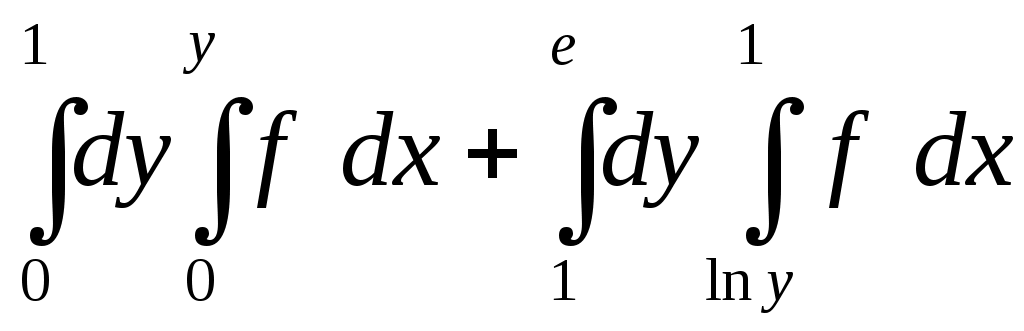 . 1.22. . 1.22. 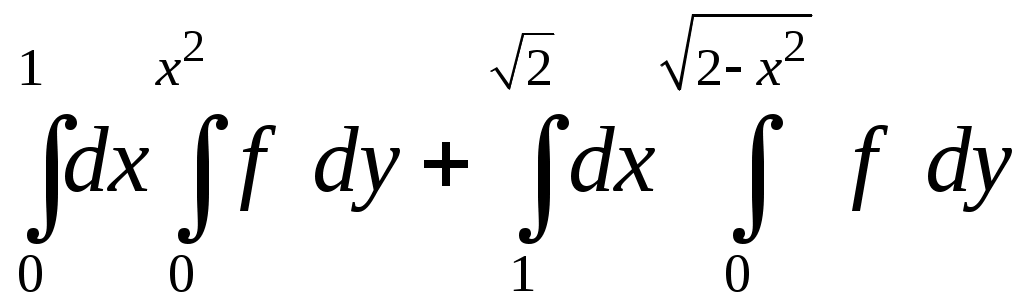 . .1.23. 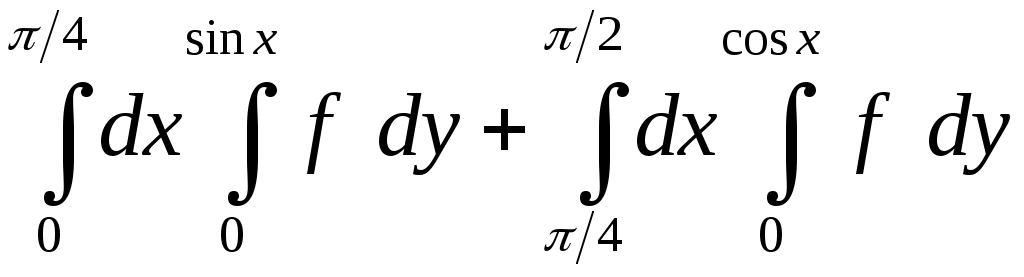 . 1.24. . 1.24. 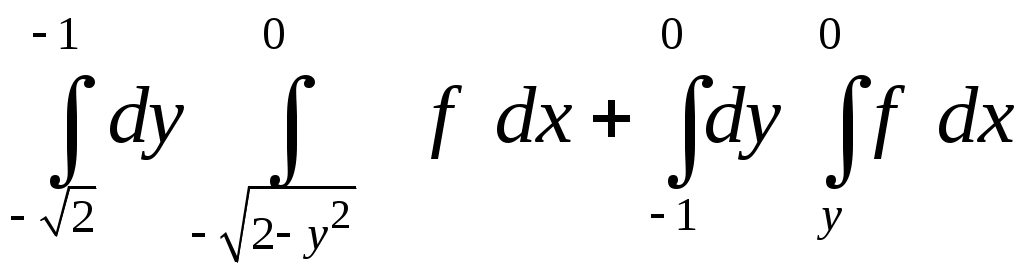 . .1.25. 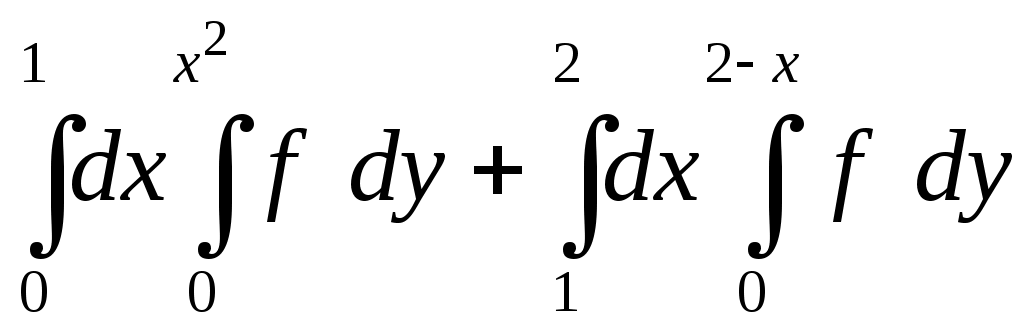 . 1.26. . 1.26. 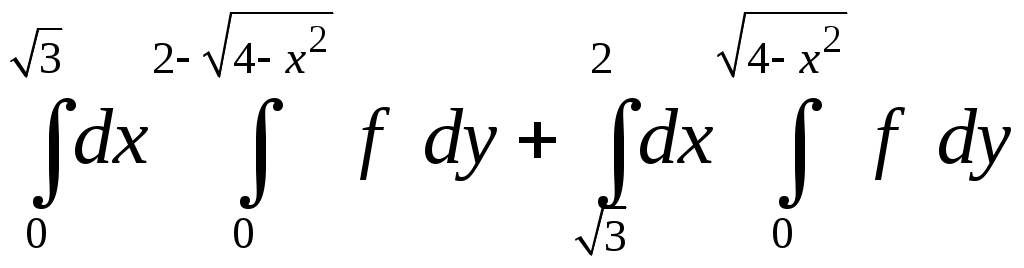 . .1.27. 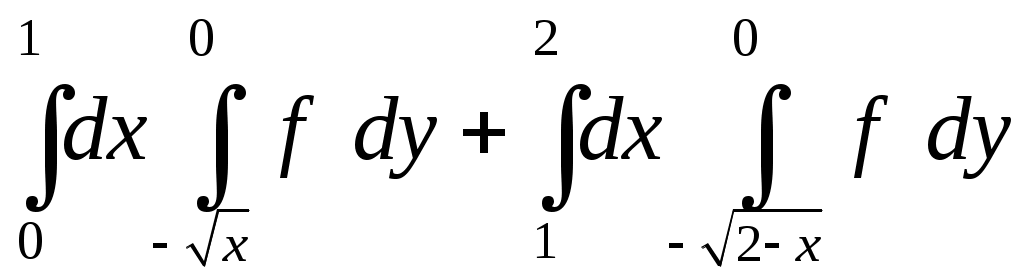 . 1.28. . 1.28. 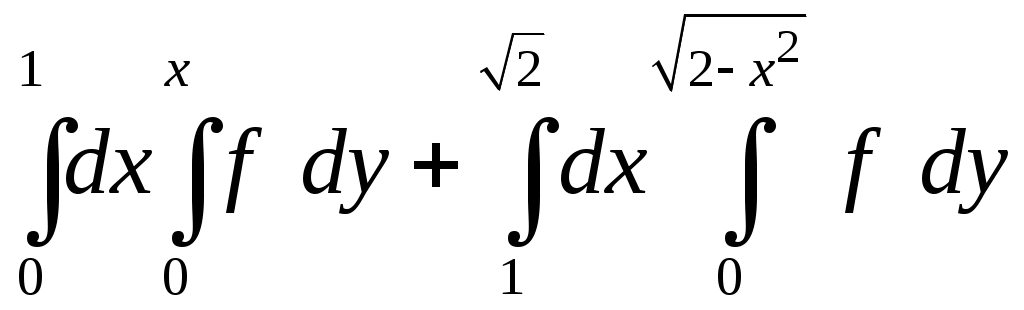 . .1.29. 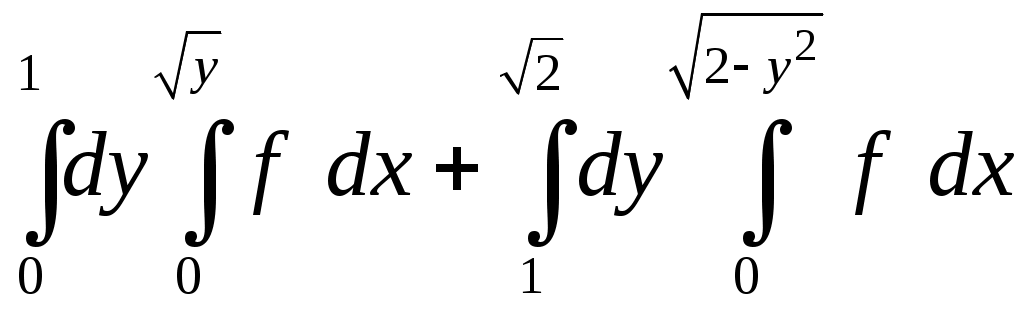 . 1.30. . 1.30. 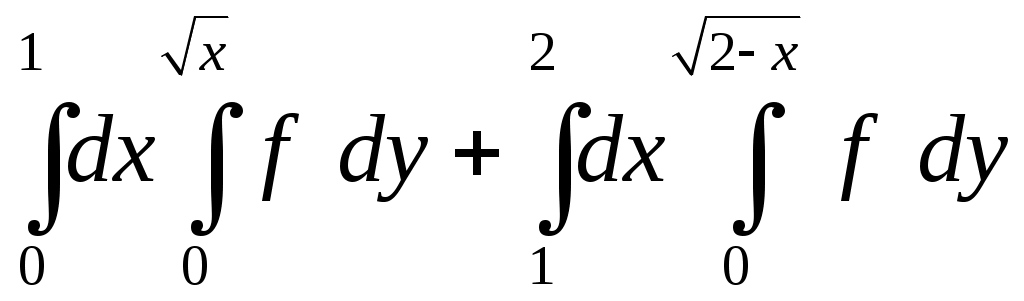 . .1.31. 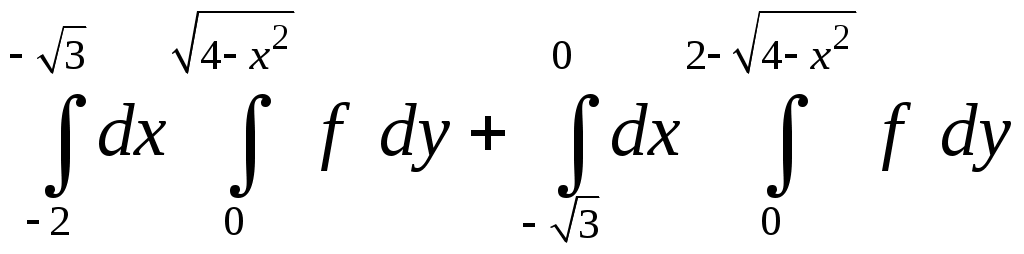 . .Задача 2. Вычислить. 2.1. 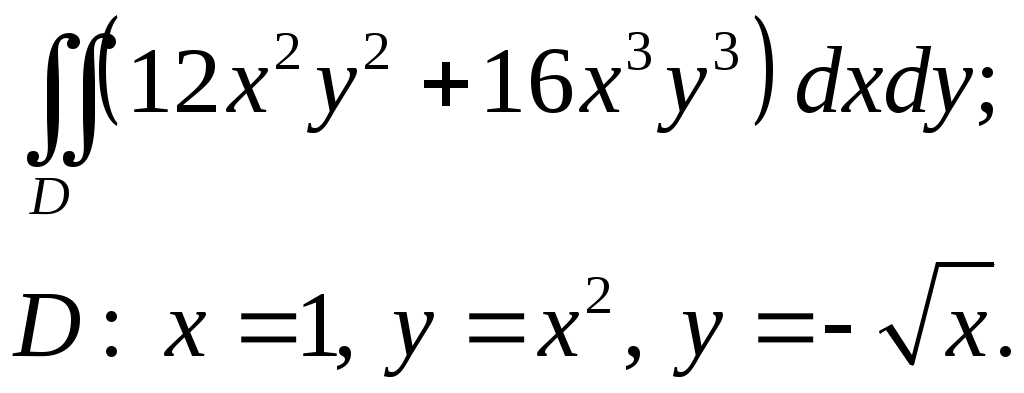 2.2. 2.2. 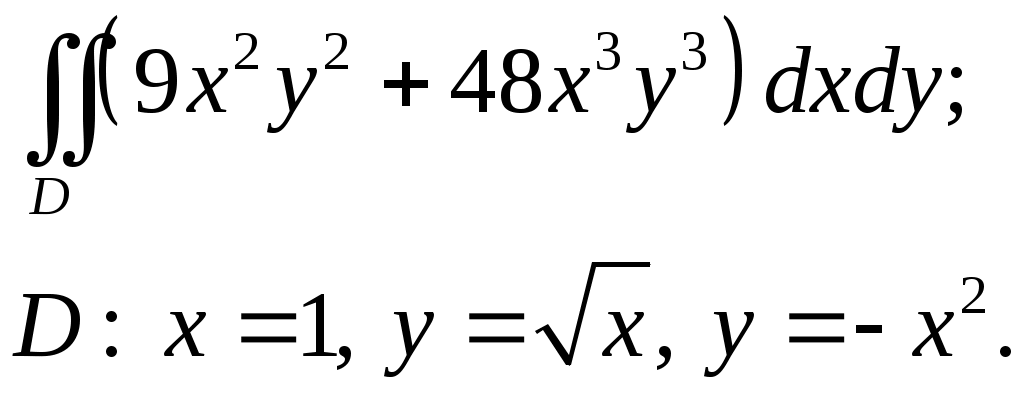 2.3. 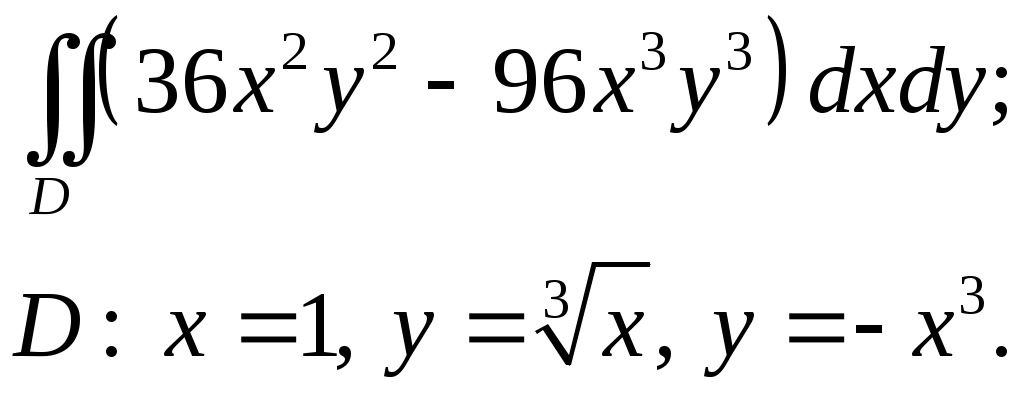 2.4. 2.4. 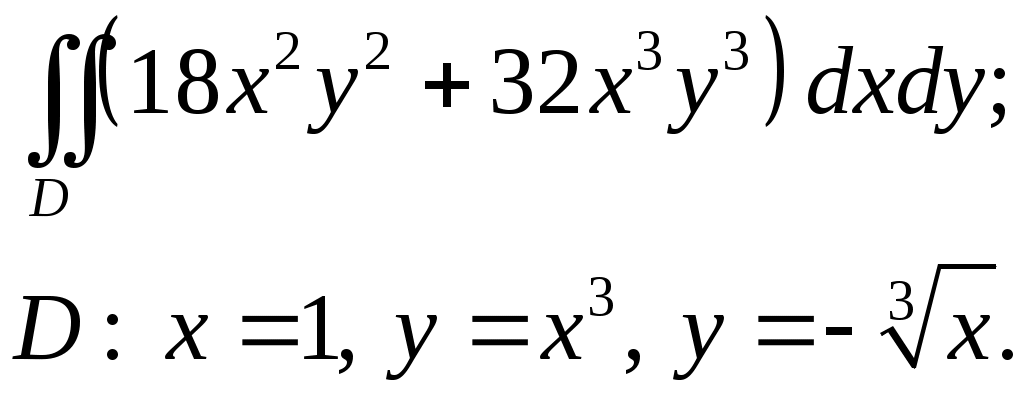 2.5. 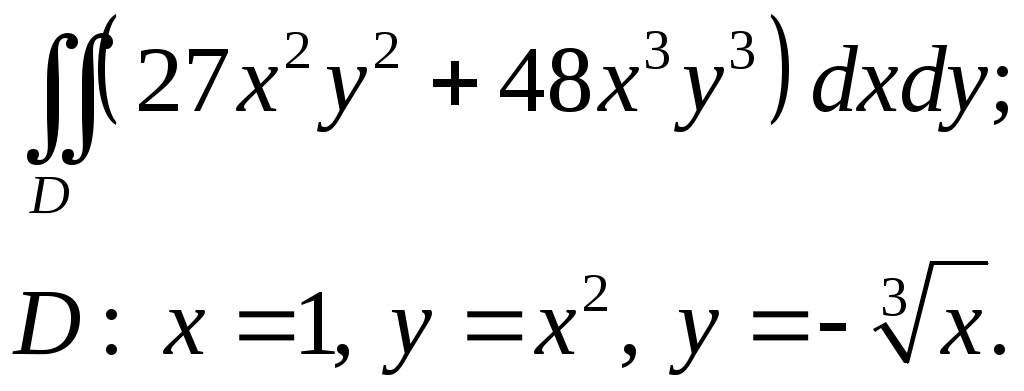 2.6. 2.6. 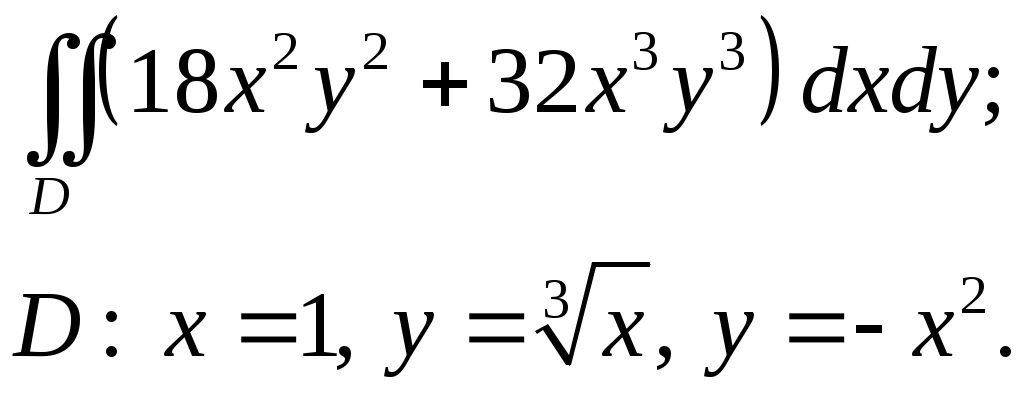 2.7. 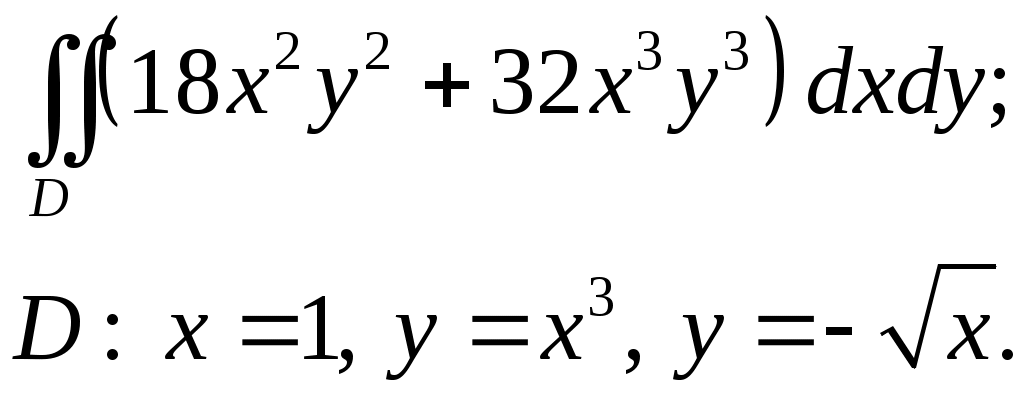 2.8. 2.8. 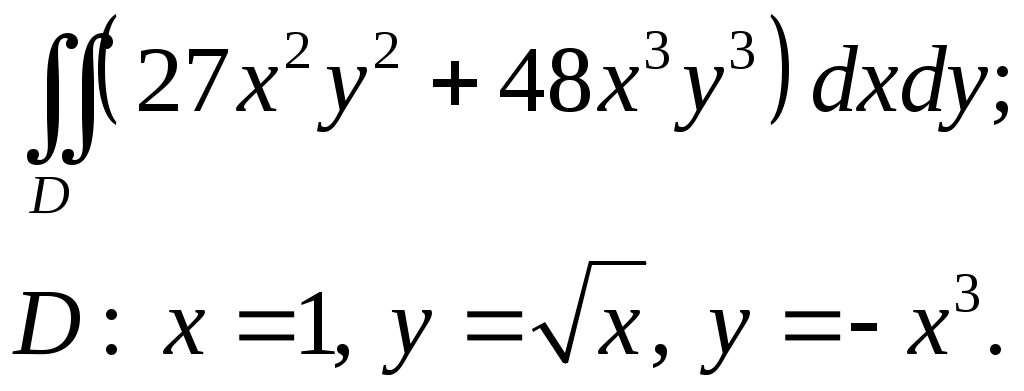 2.9. 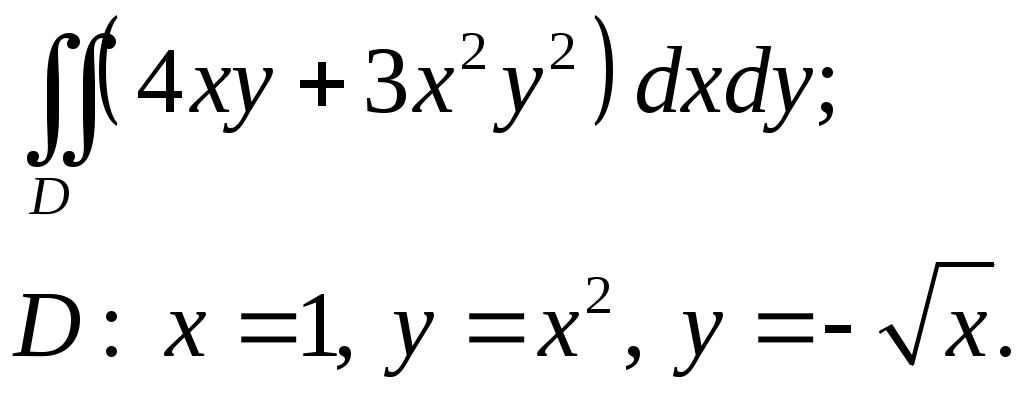 2.10. 2.10. 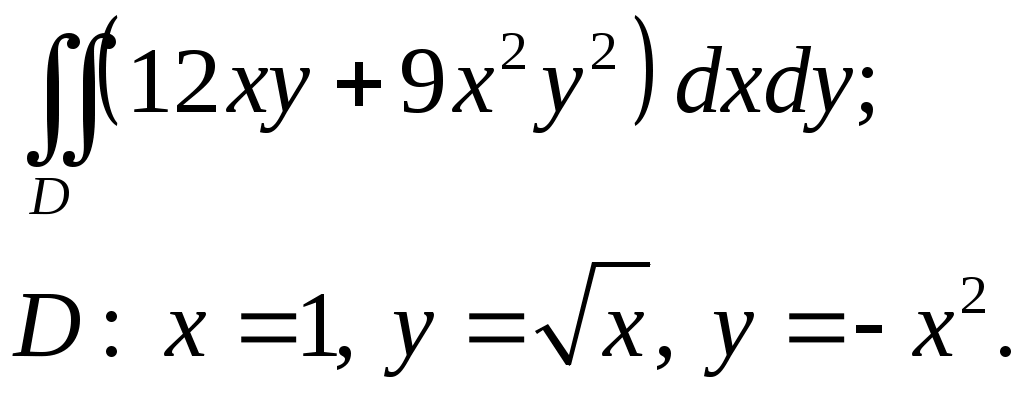 2.11. 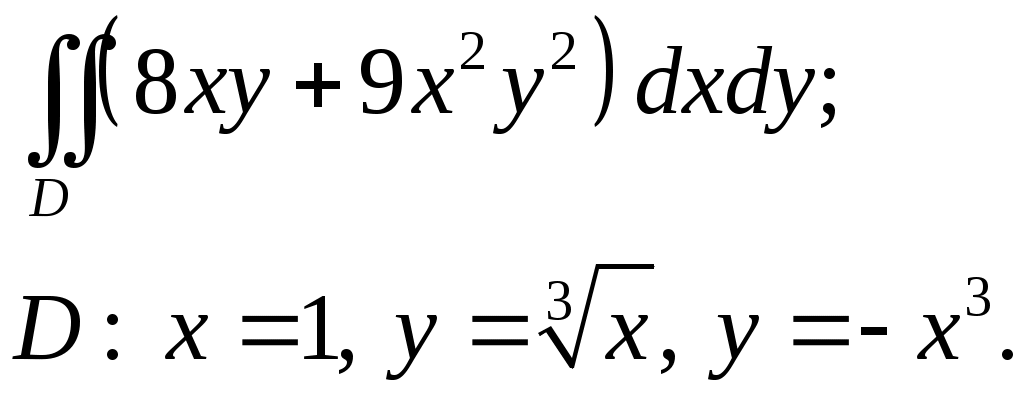 2.12. 2.12. 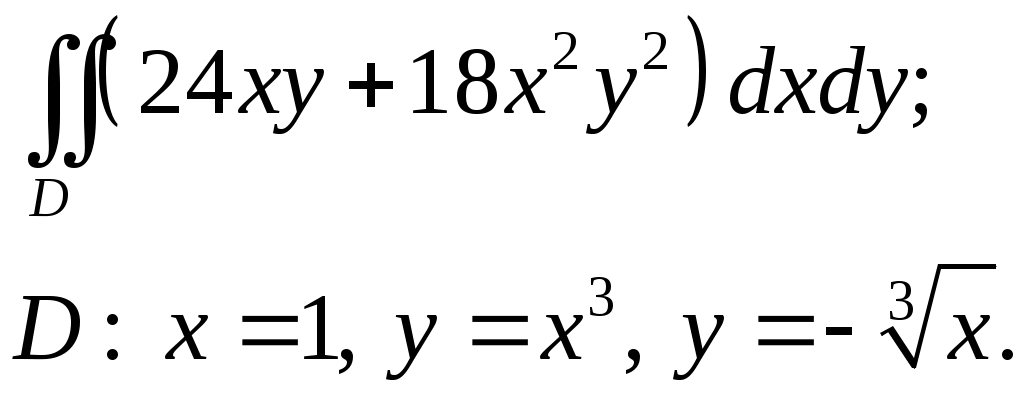 2.13. 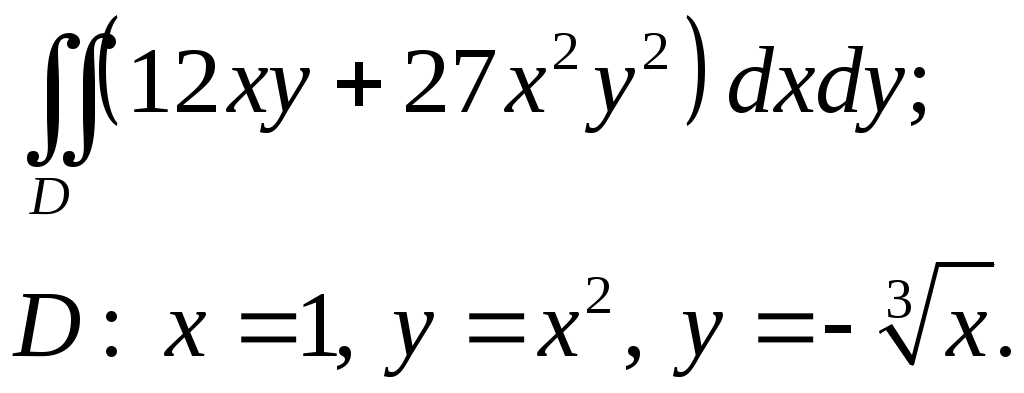 2.14. 2.14. 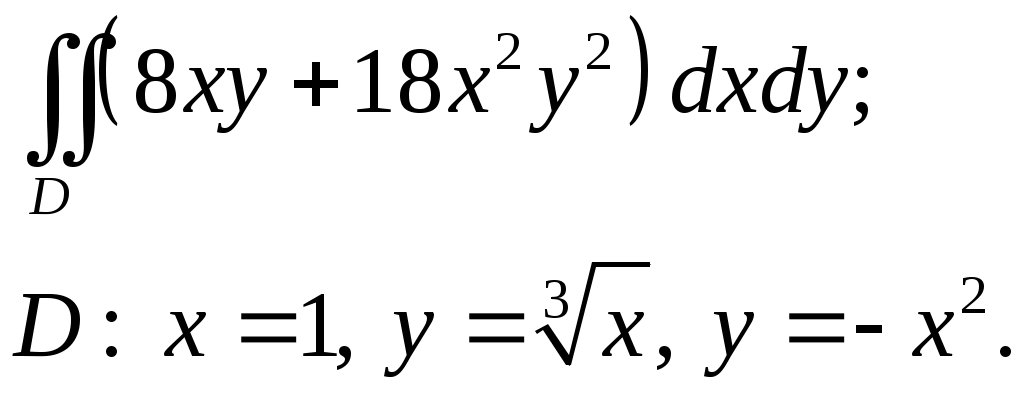 2.15. 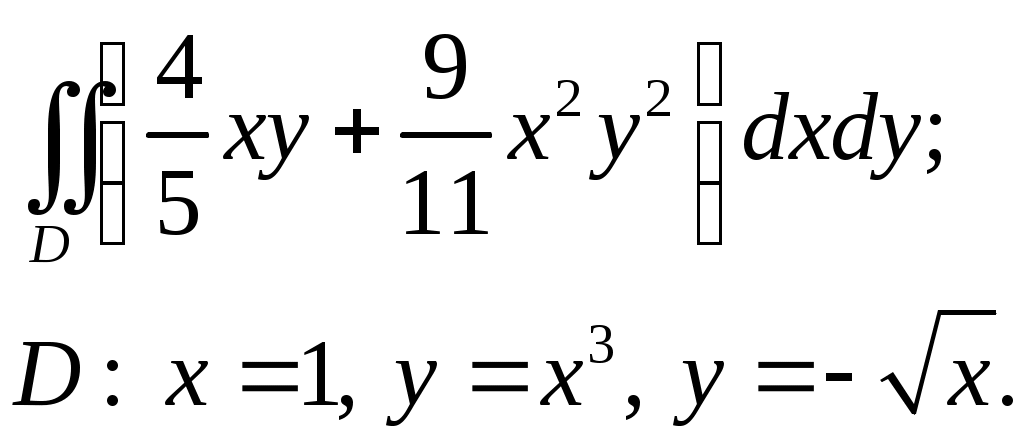 2.16. 2.16. 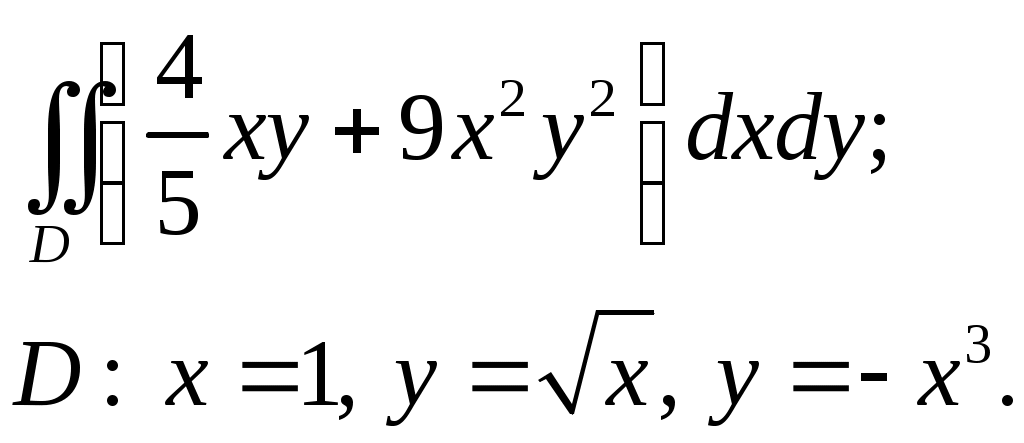 2.17. 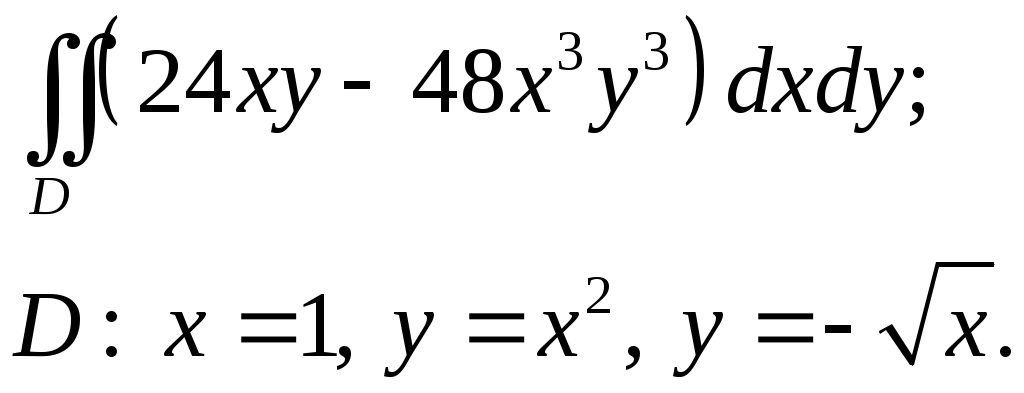 2.18. 2.18. 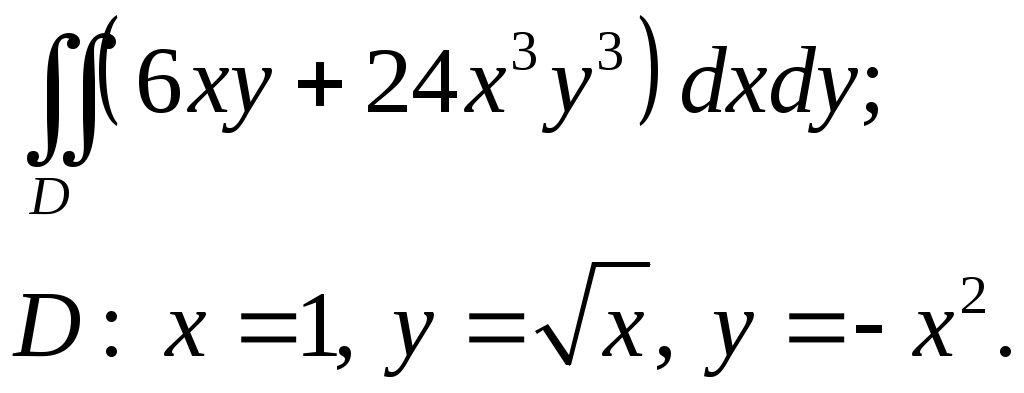 2.19. 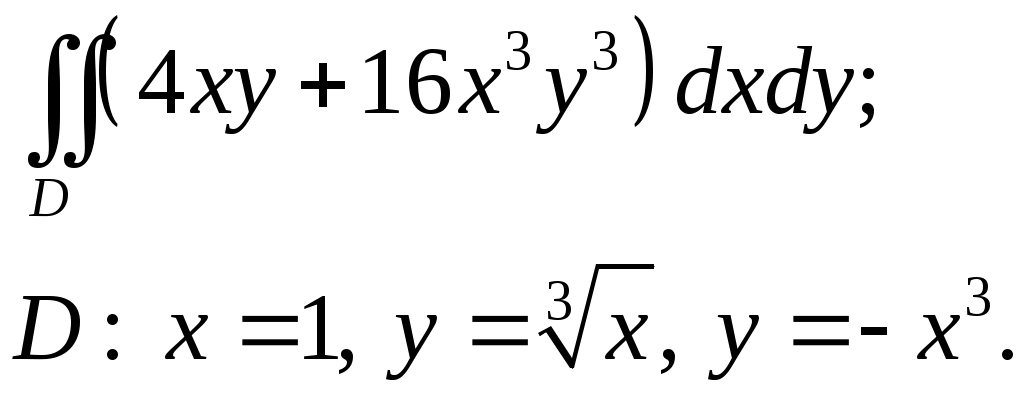 2.20. 2.20. 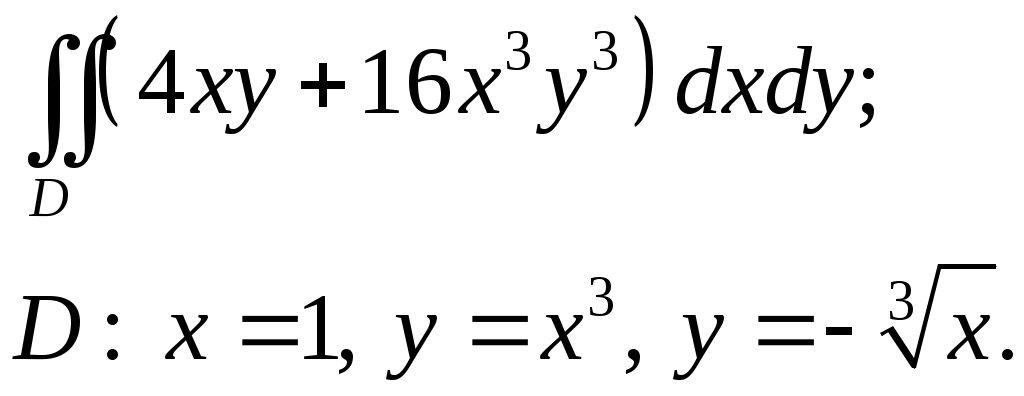 2.21. 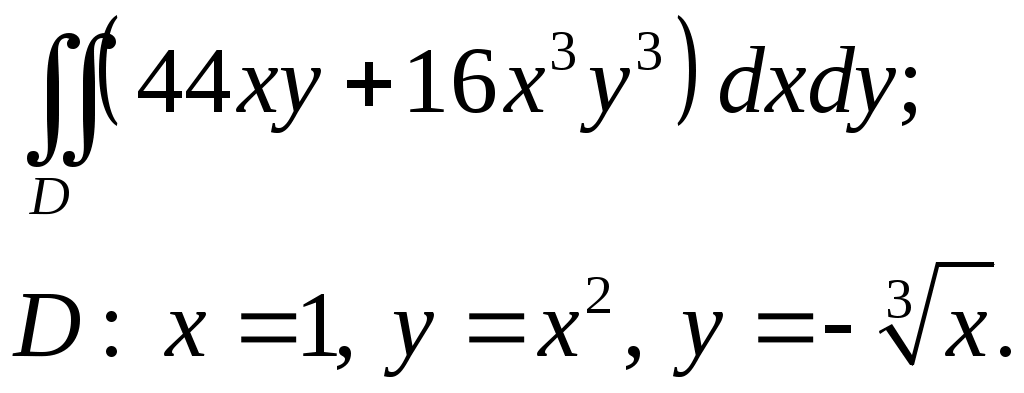 2.22. 2.22. 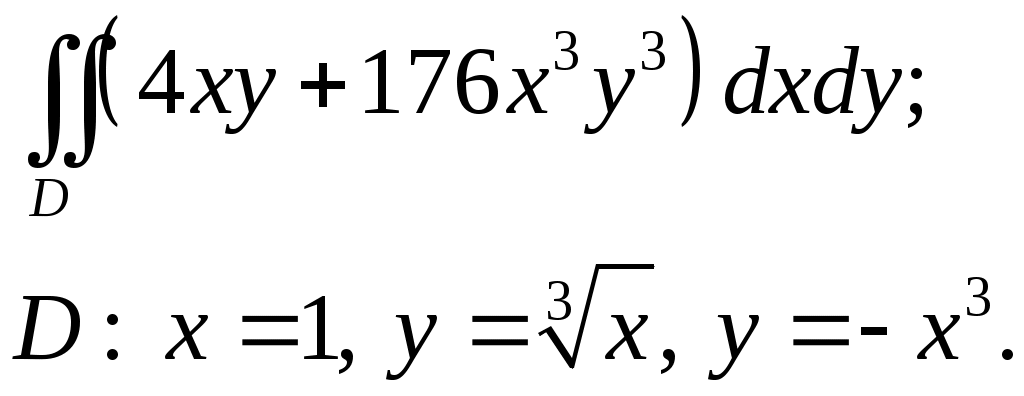 2.23. 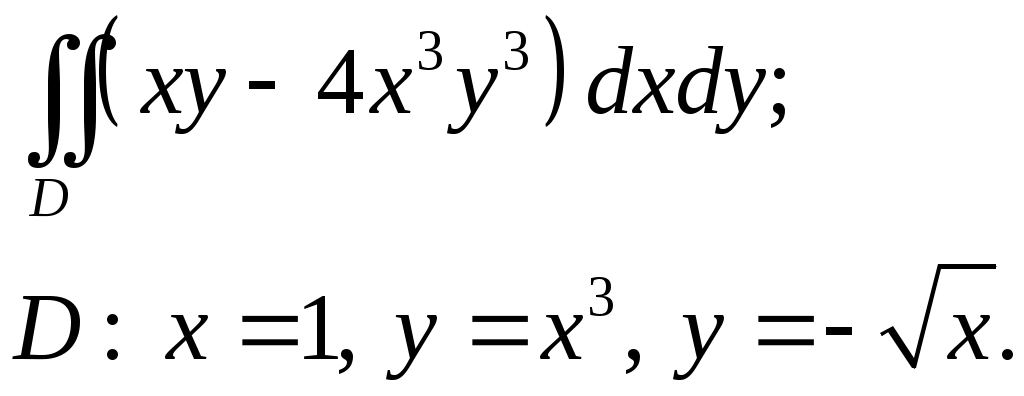 2.24. 2.24. 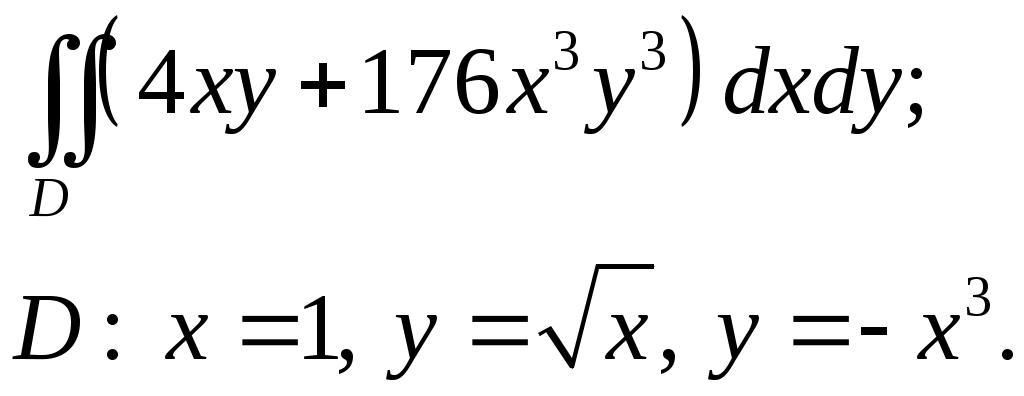 2.25. 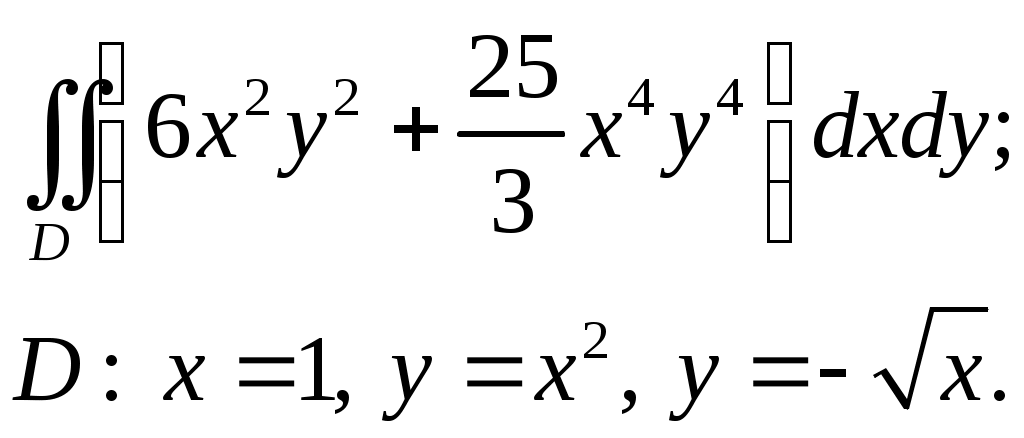 2.26. 2.26. 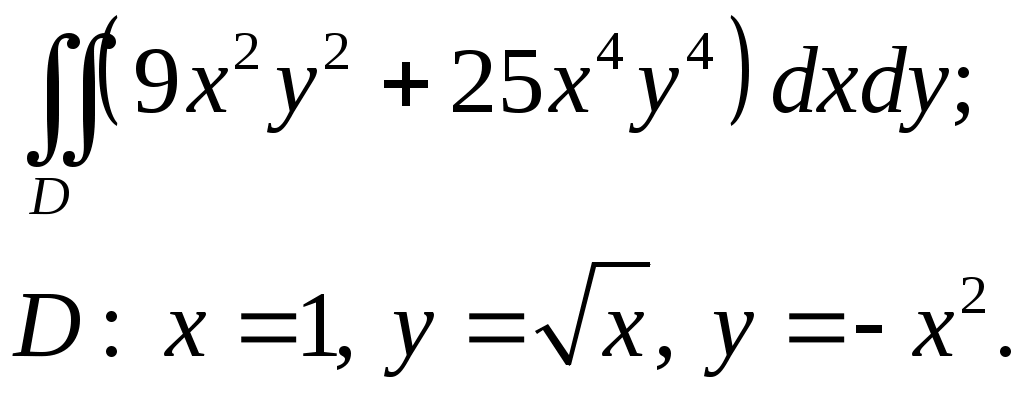 2.27. 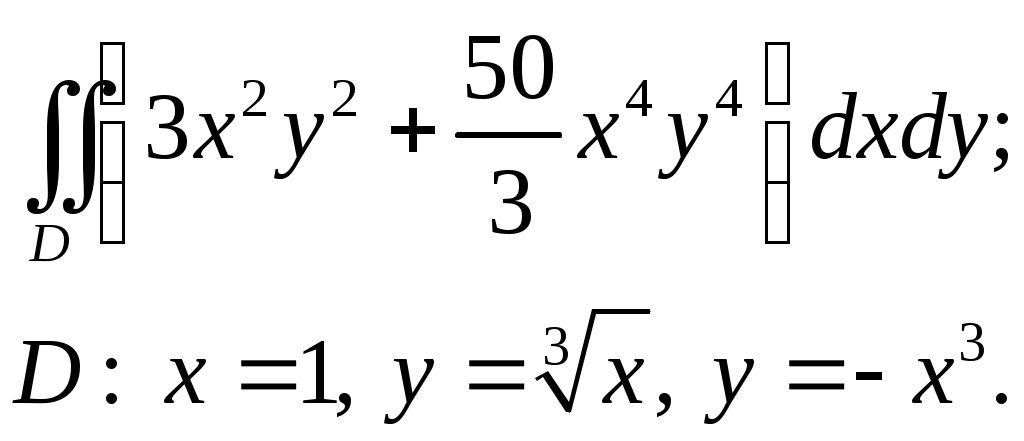 2.28. 2.28. 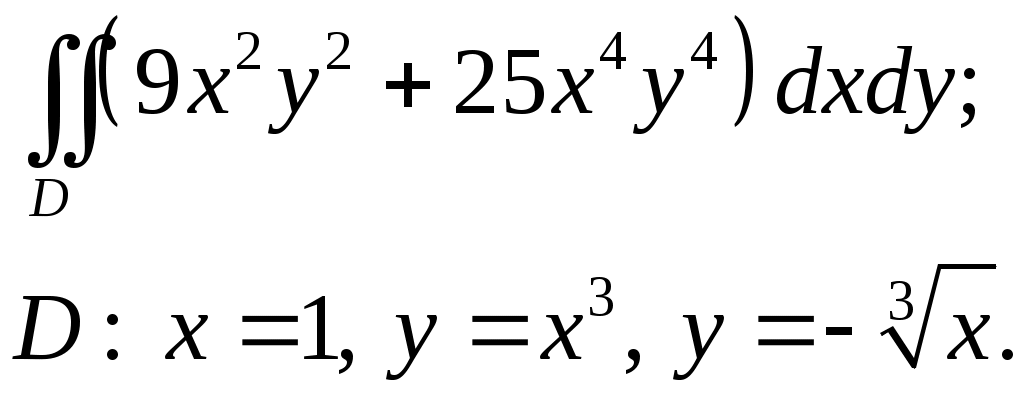 2.29. 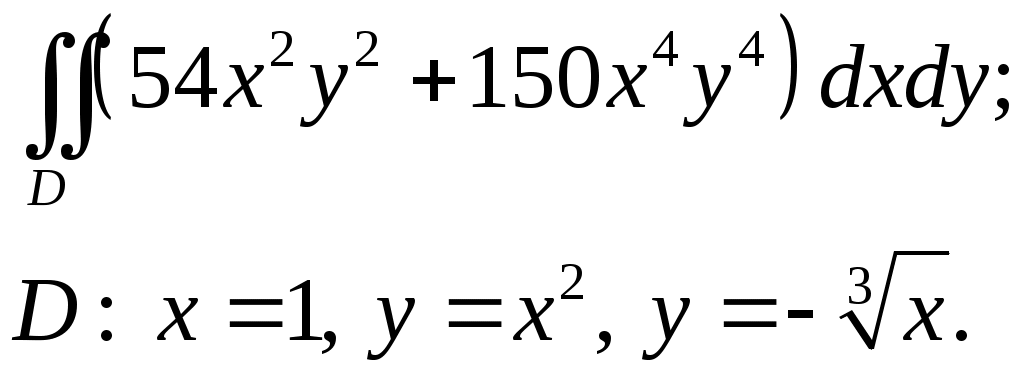 2.30. 2.30. 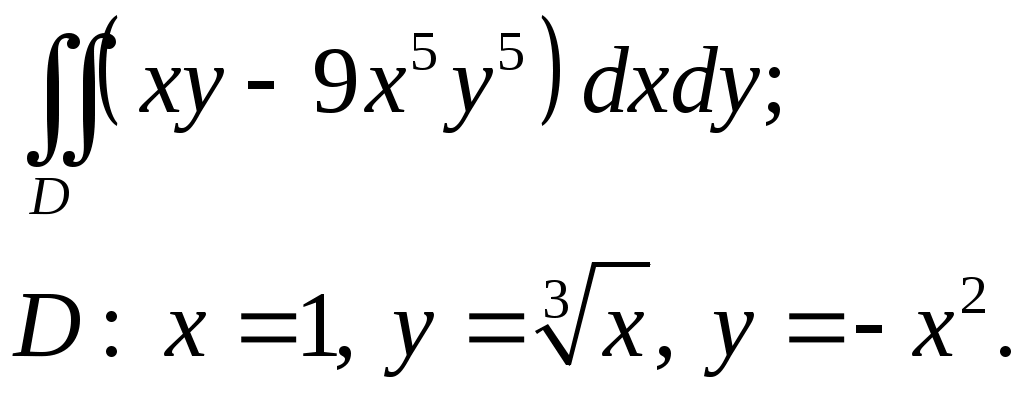 2.31. 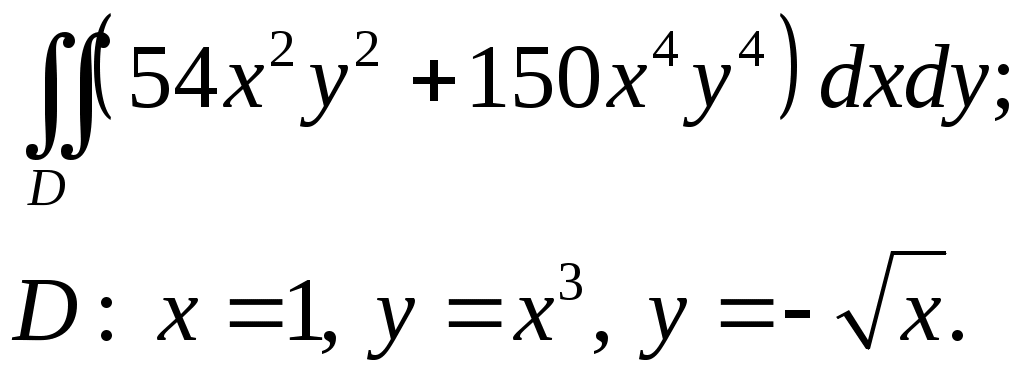 Задача 3. Вычислить. 3.1. 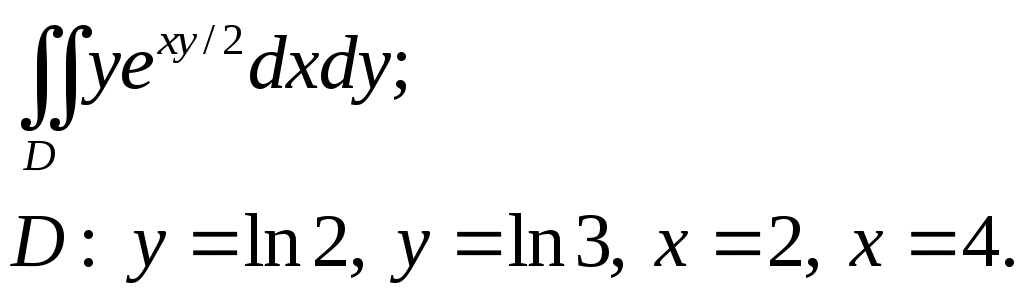 3.2. 3.2. 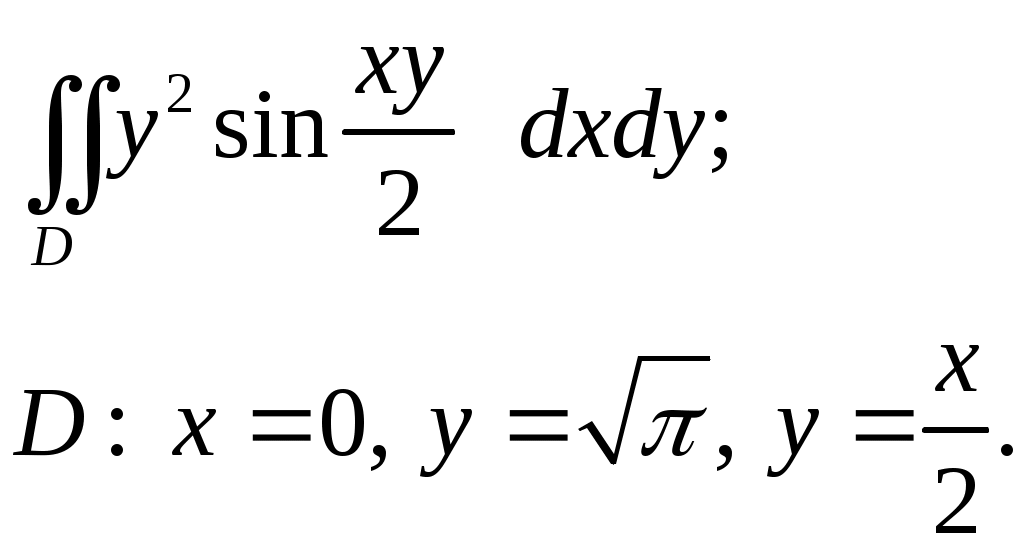 3.3. 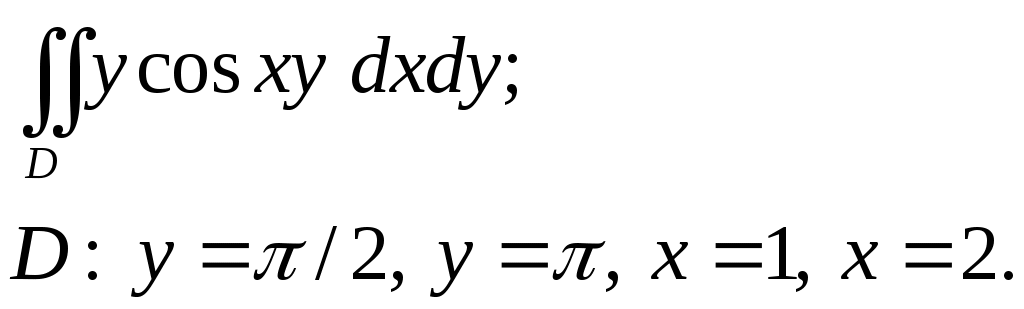 3.4. 3.4. 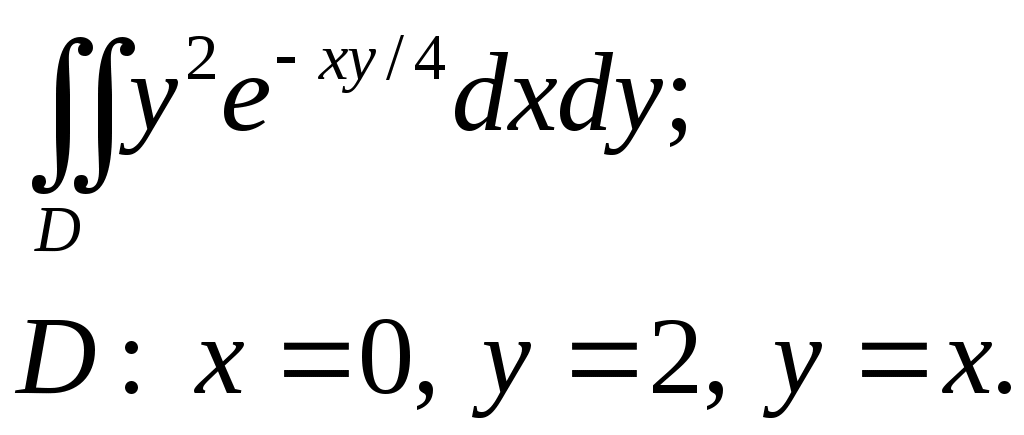 3.5. 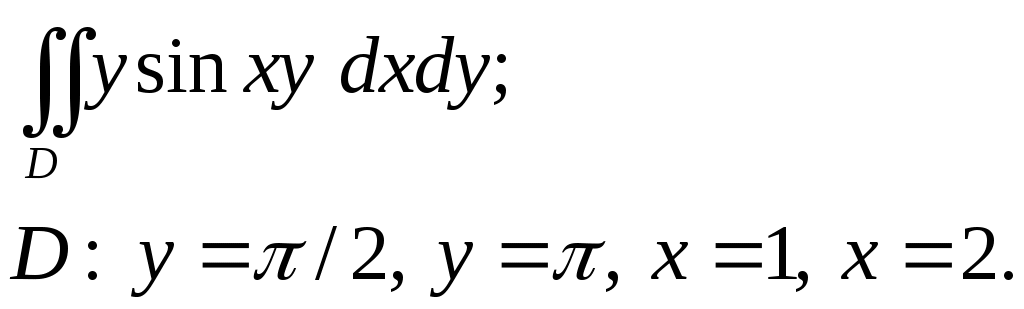 3.6. 3.6. 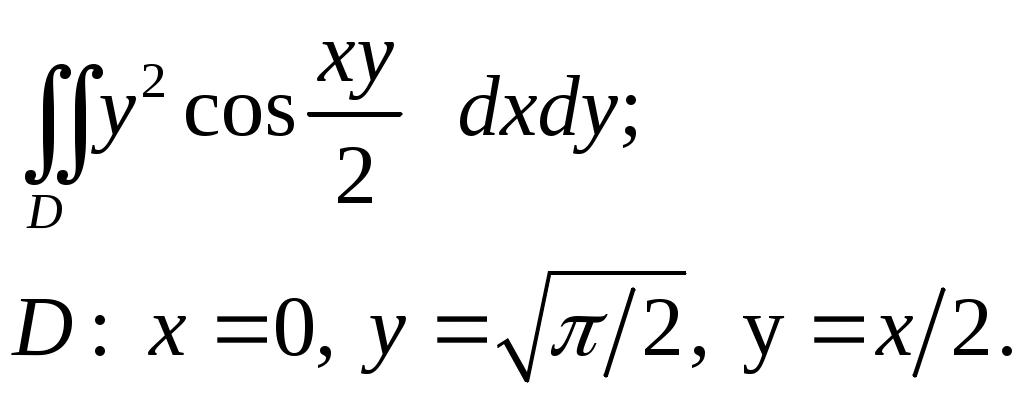 3.7. 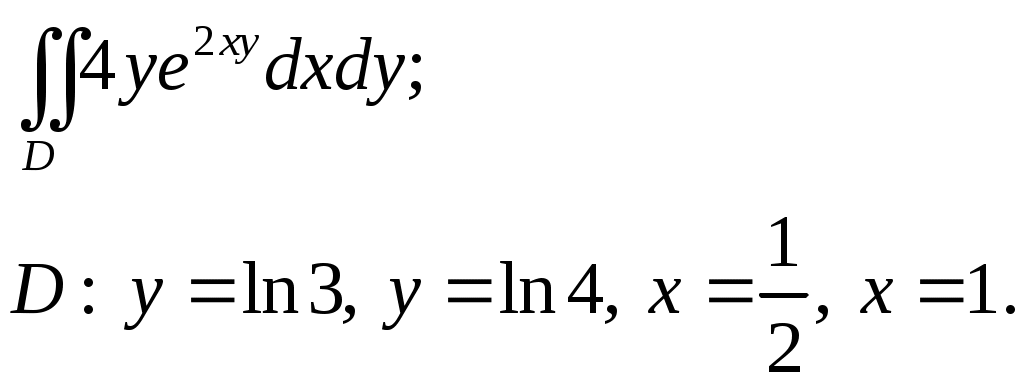 3.8. 3.8. 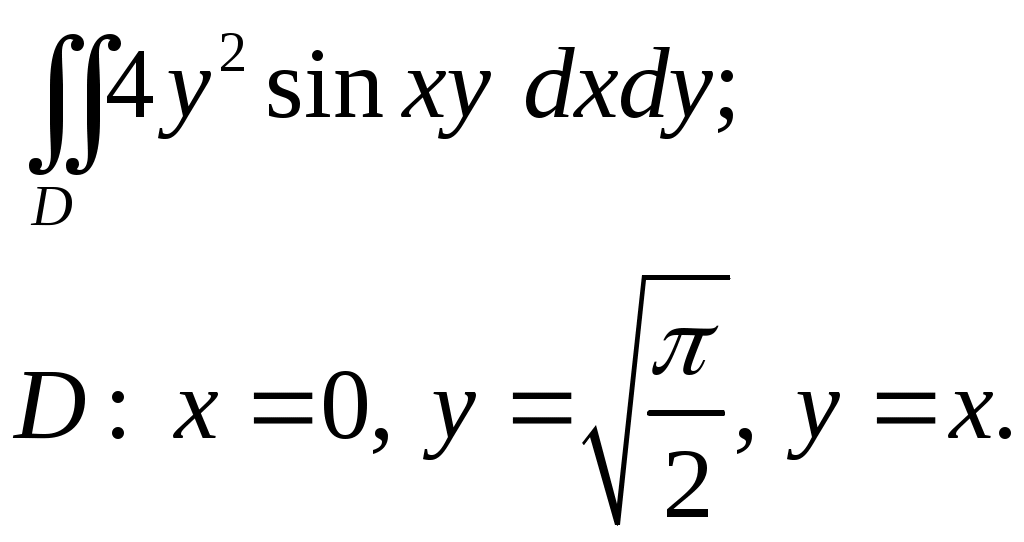 3.9. 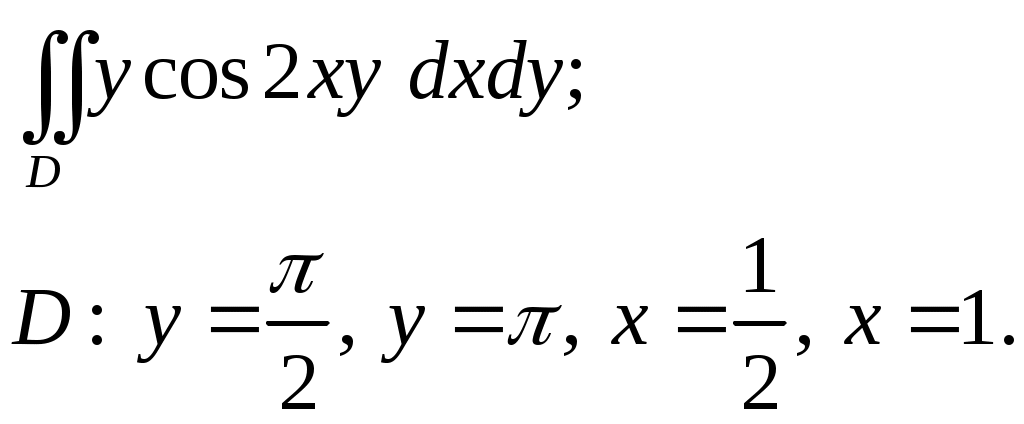 3.10. 3.10. 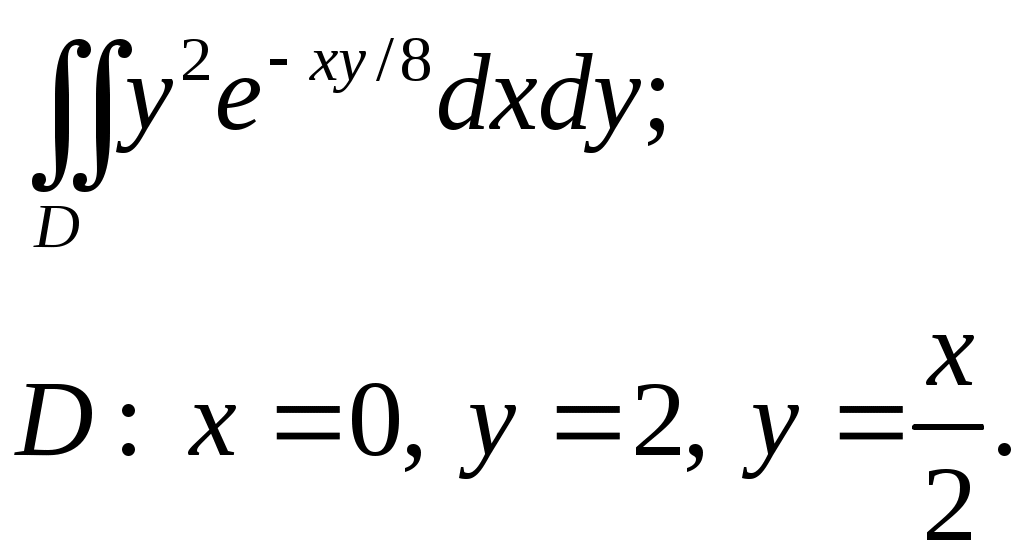 3.11. 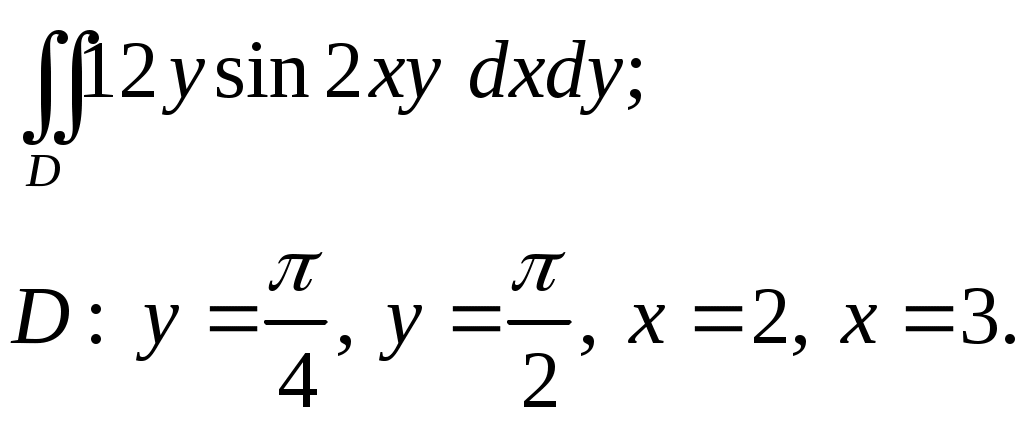 3.12. 3.12. 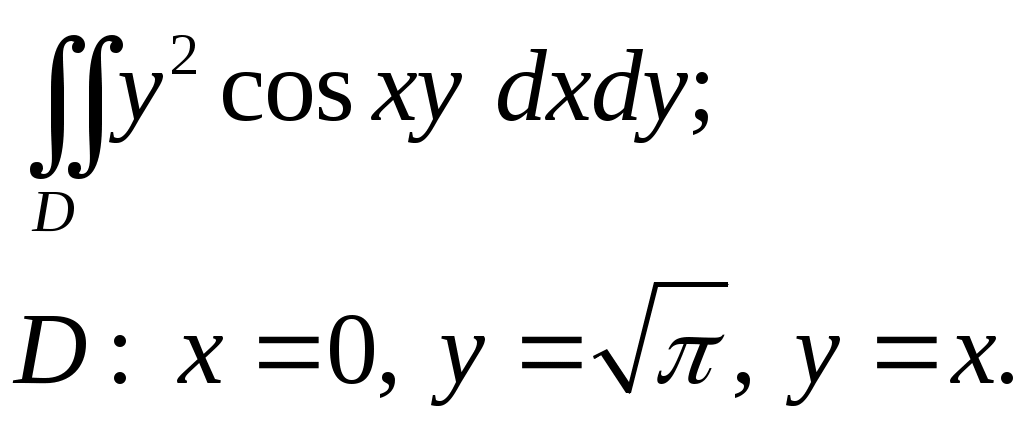 3.13. 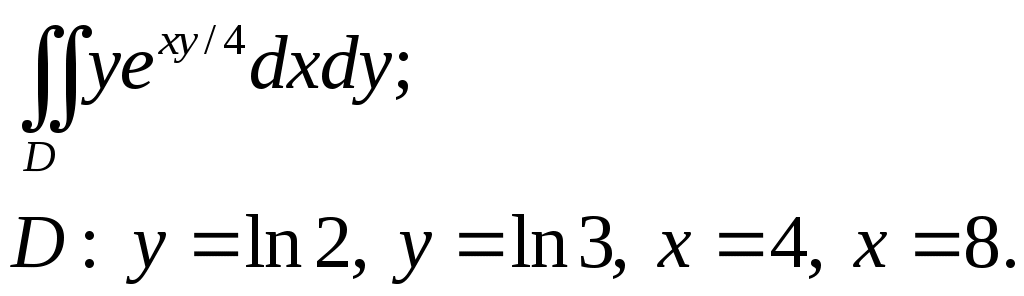 3.14. 3.14. 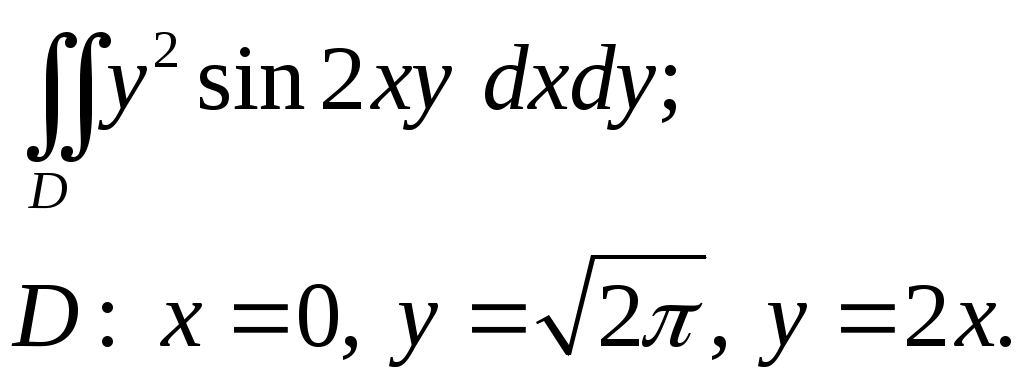 3.15. 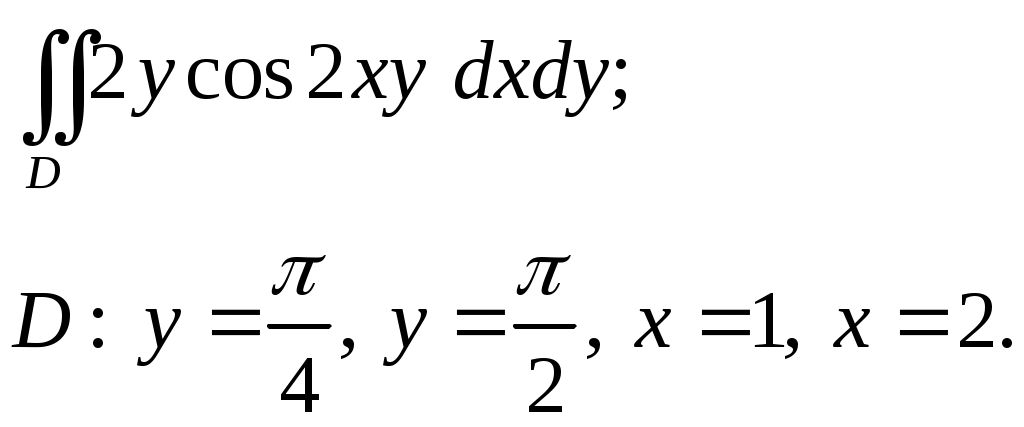 3.16. 3.16. 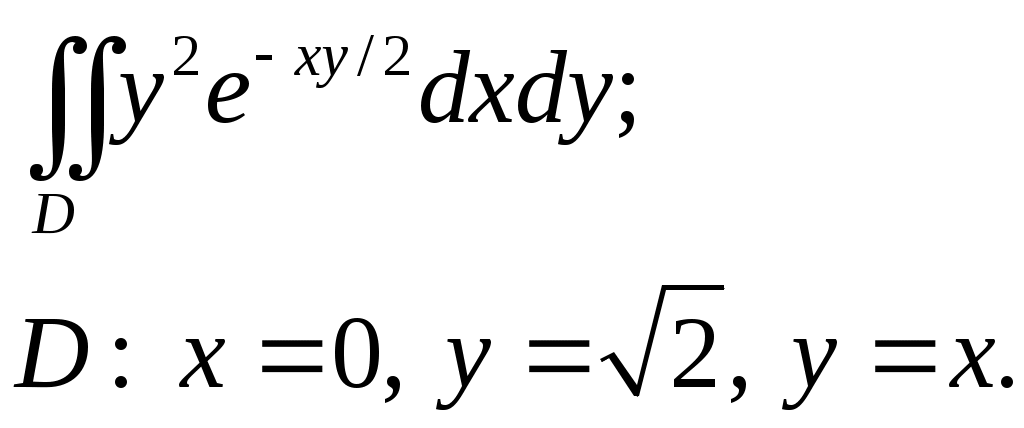 3.17. 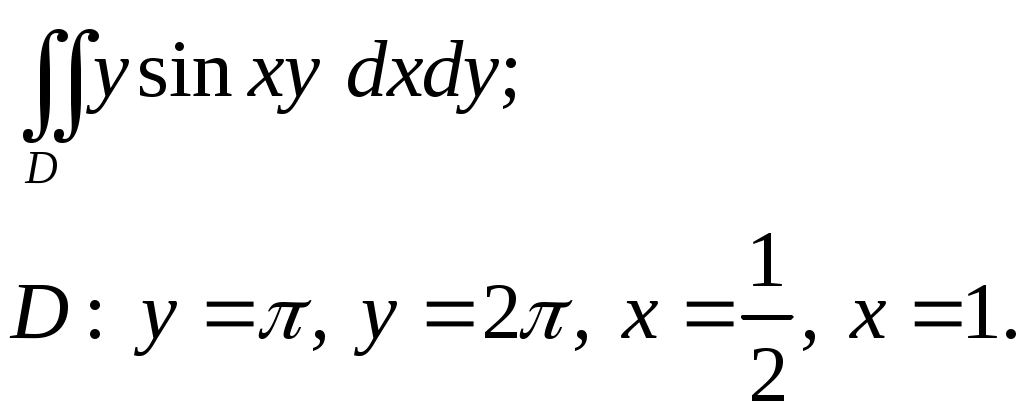 3.18. 3.18. 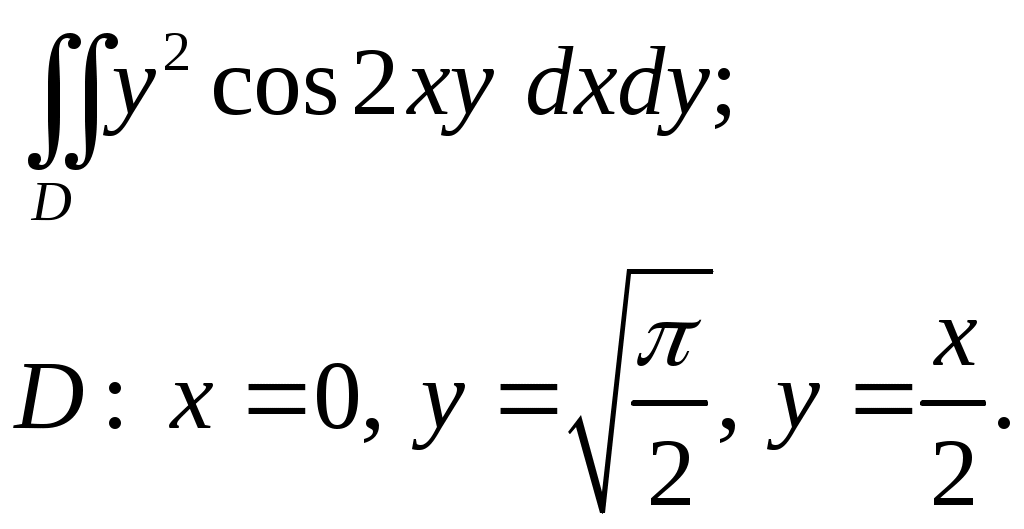 3.19. 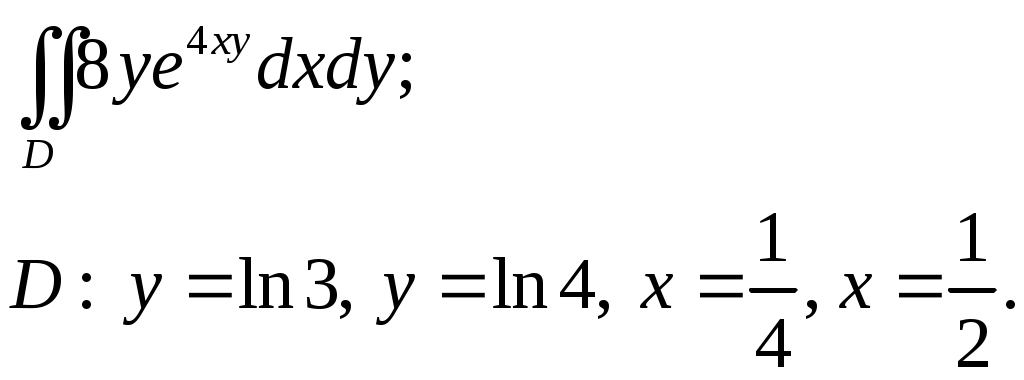 3.20. 3.20. 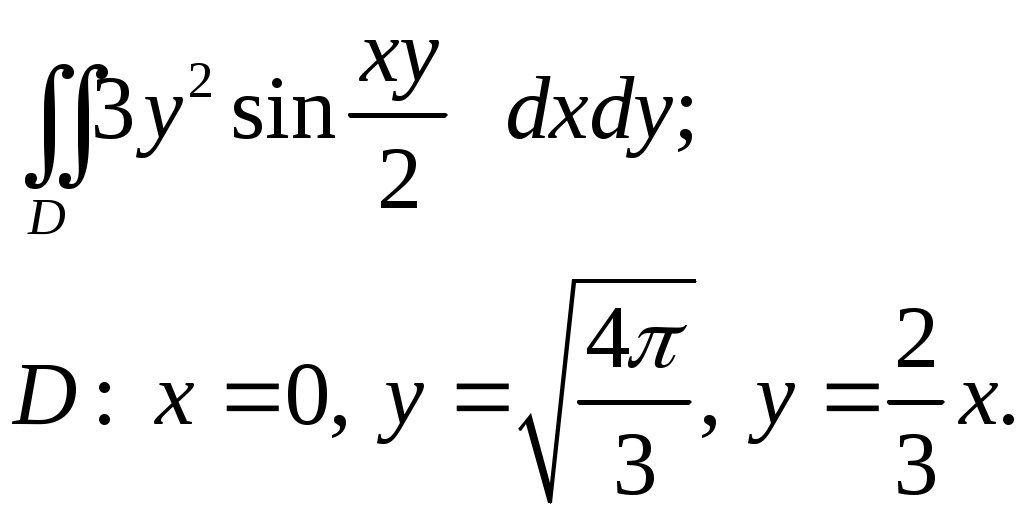 3.21. 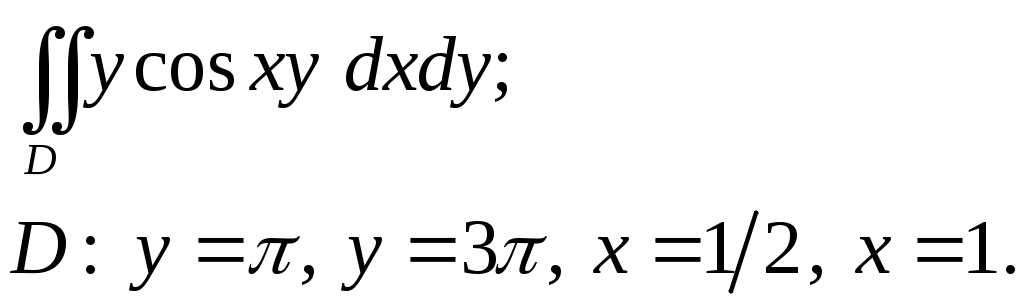 3.22. 3.22. 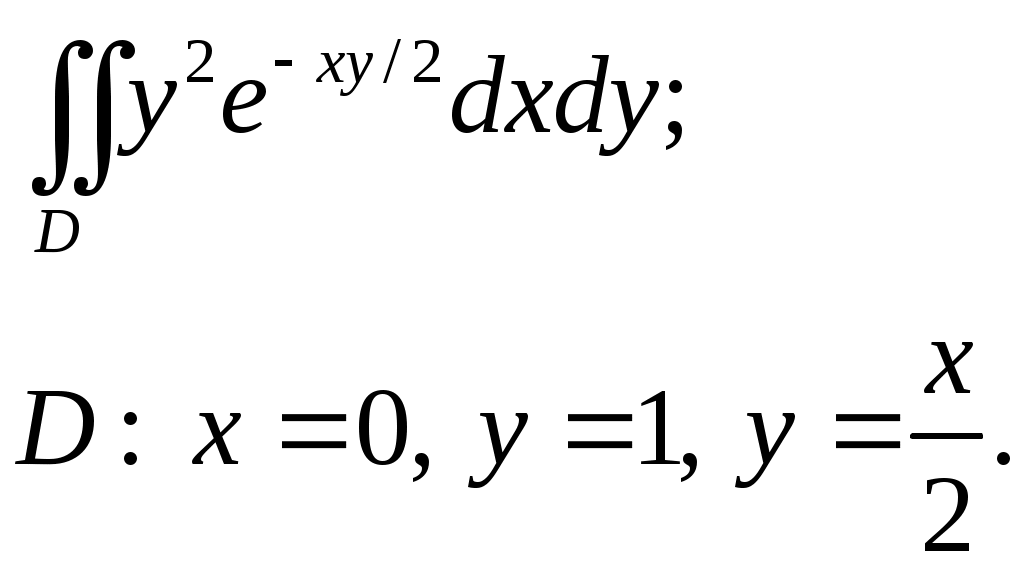 3.23. 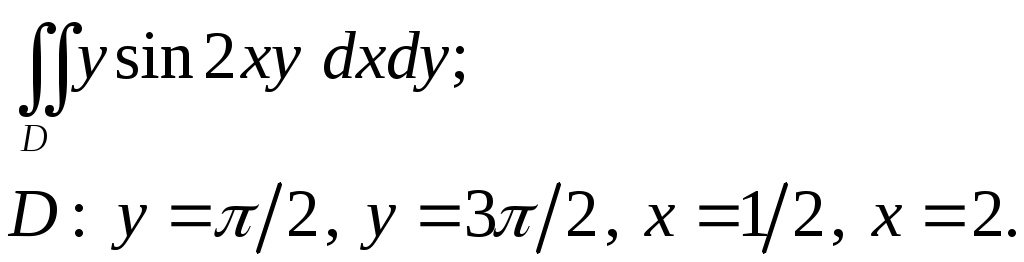 3.24. 3.24. 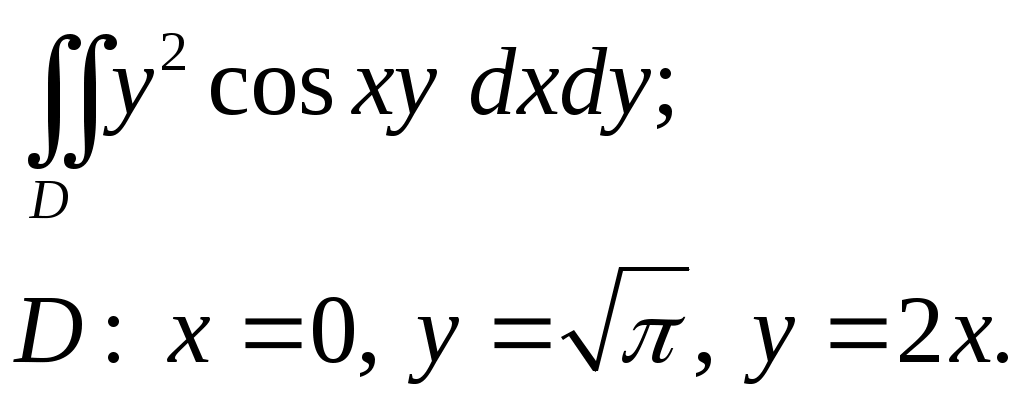 3.25. 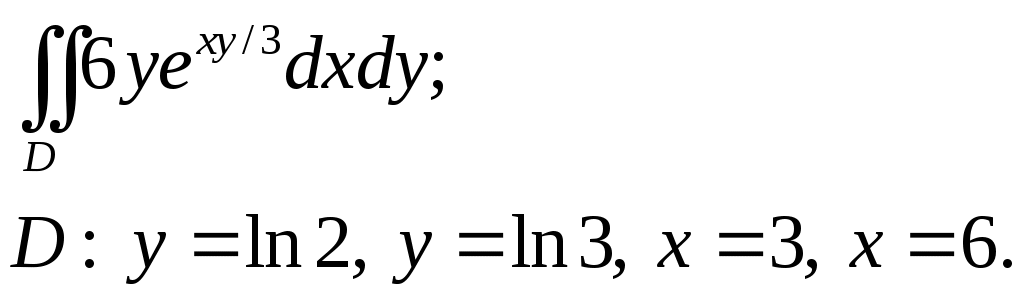 3.26. 3.26. 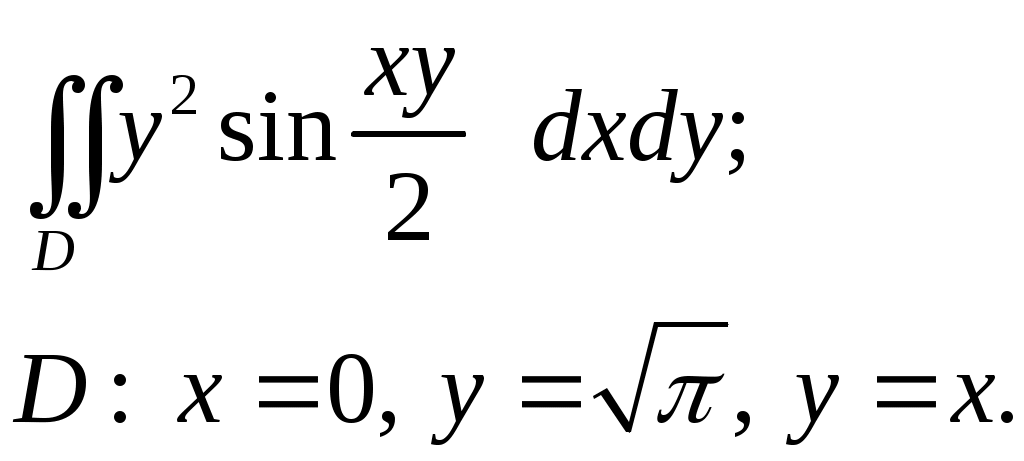 3.27. 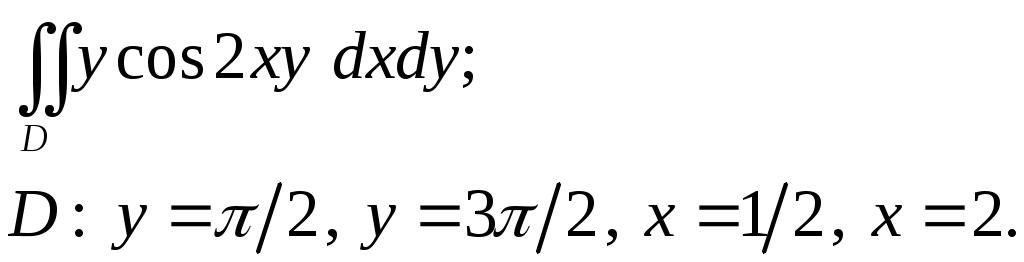 3.28. 3.28. 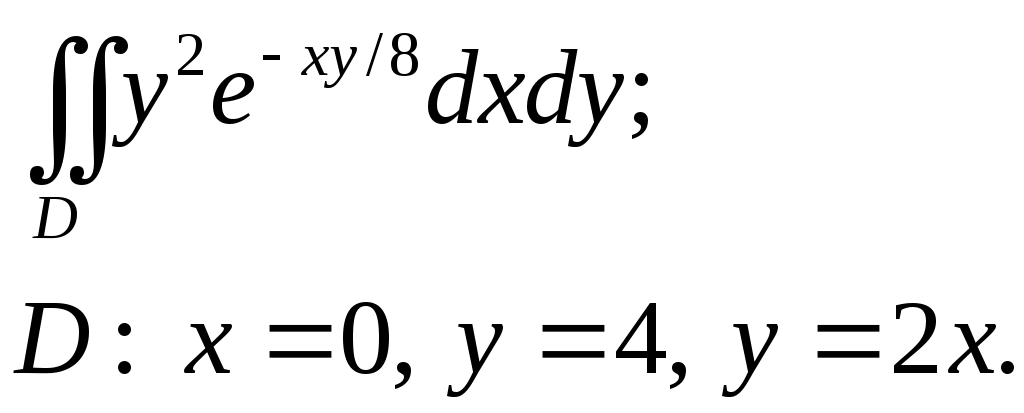 3.29. 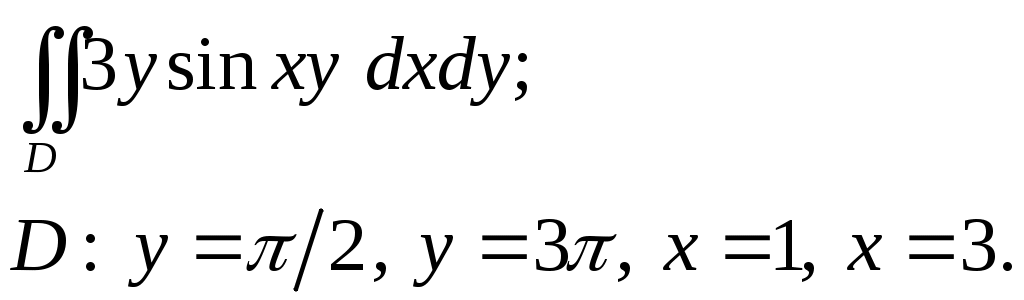 3.30. 3.30. 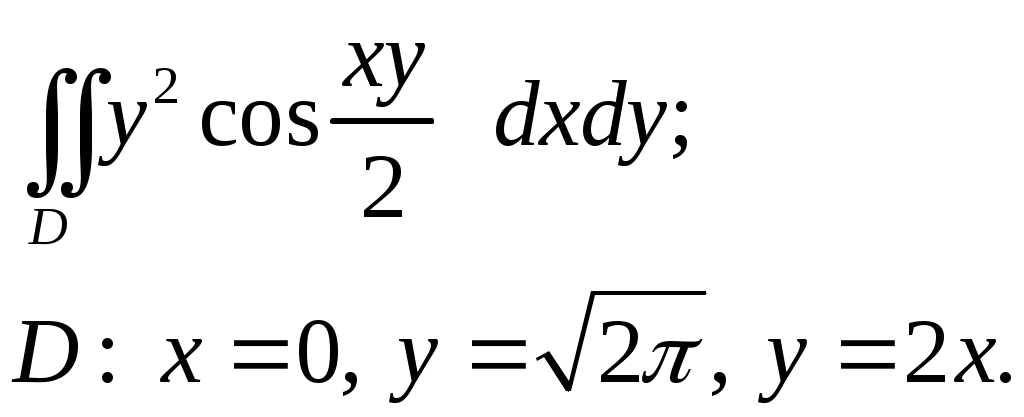 3.31. 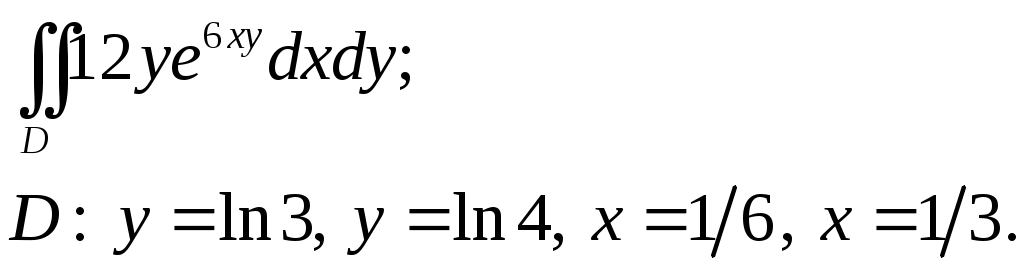 Задача 4. Вычислить. 4.1. 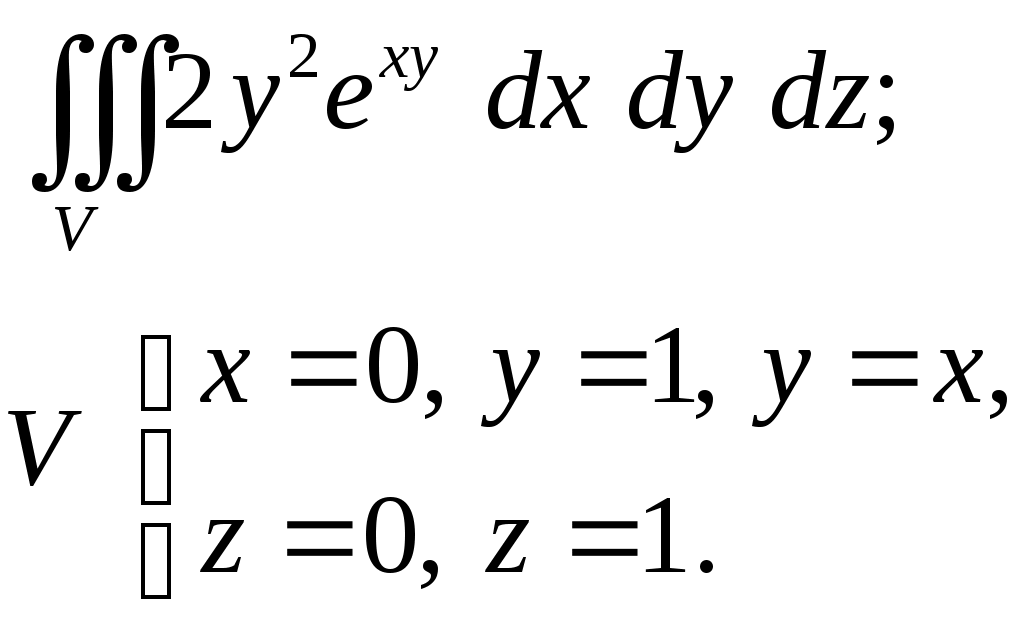 4.2. 4.2. 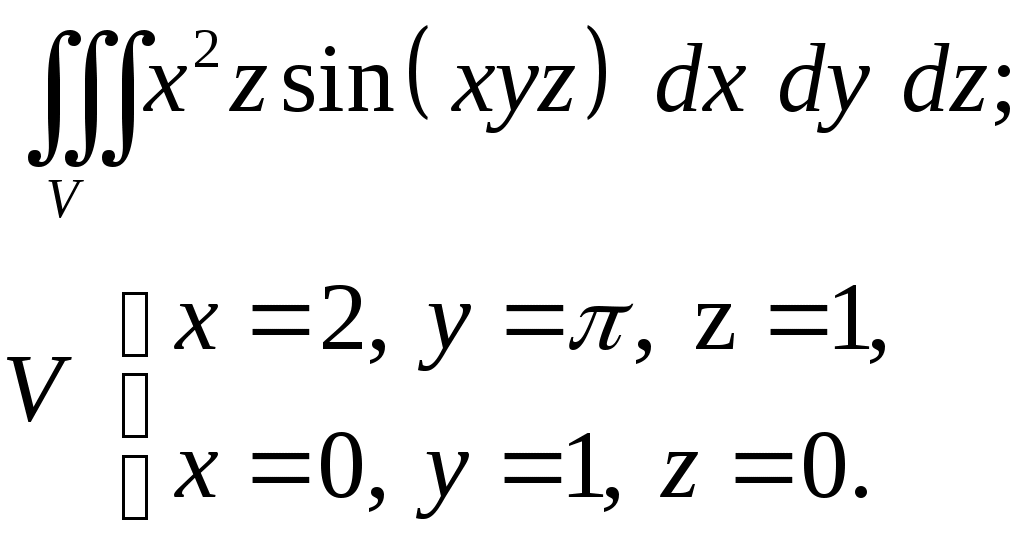 4.3. 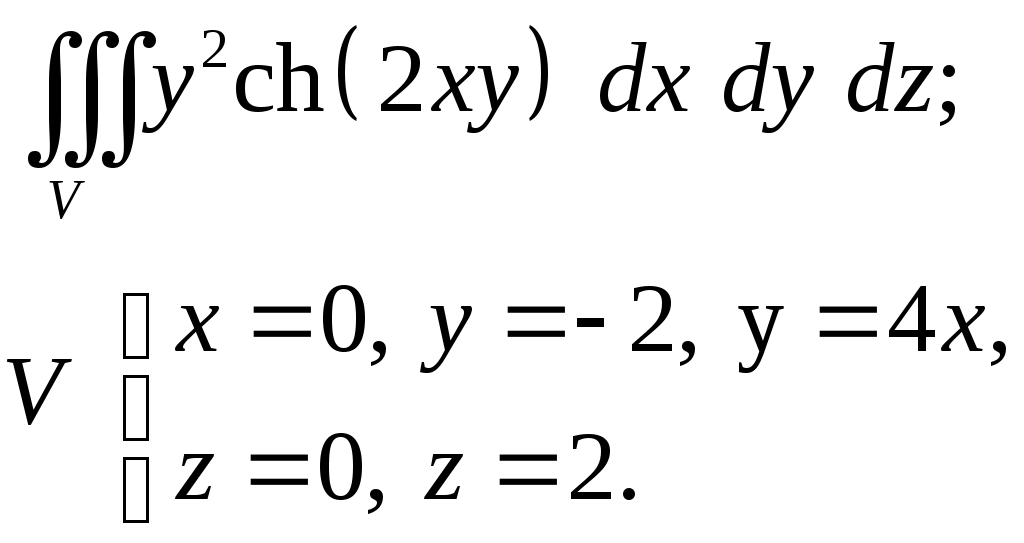 4.4. 4.4. 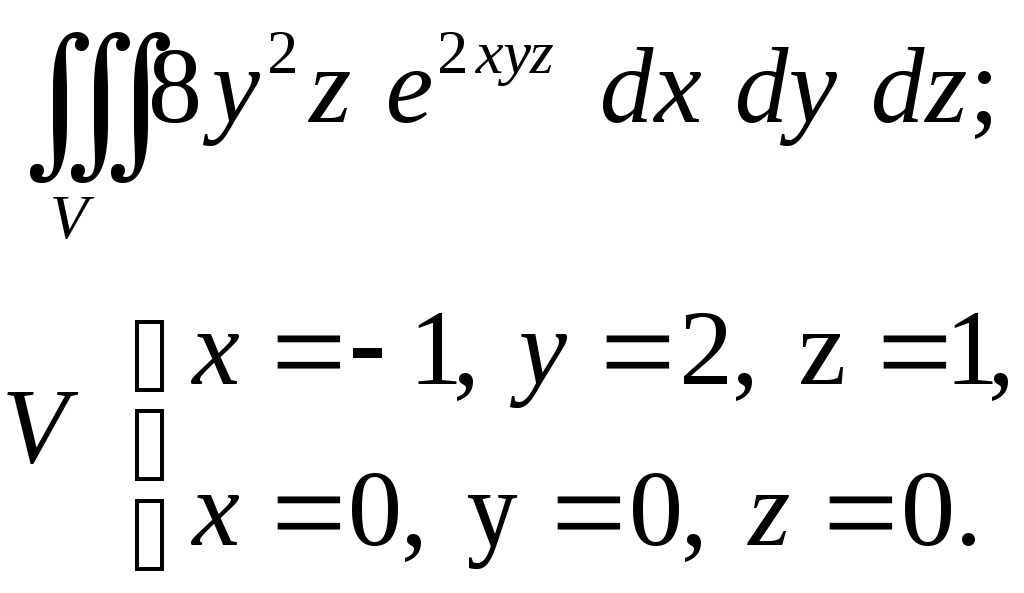 4.5. 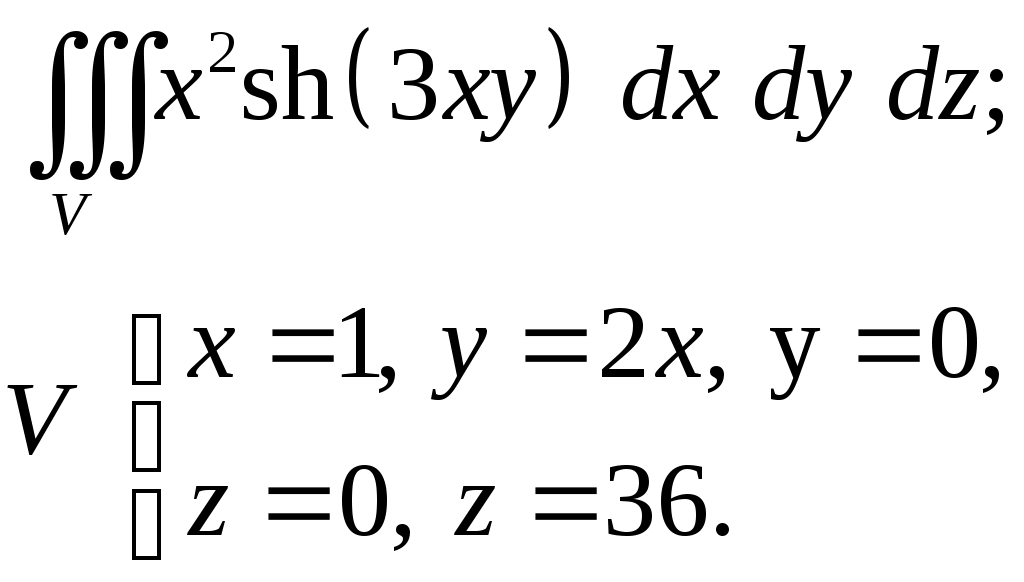 4.6. 4.6. 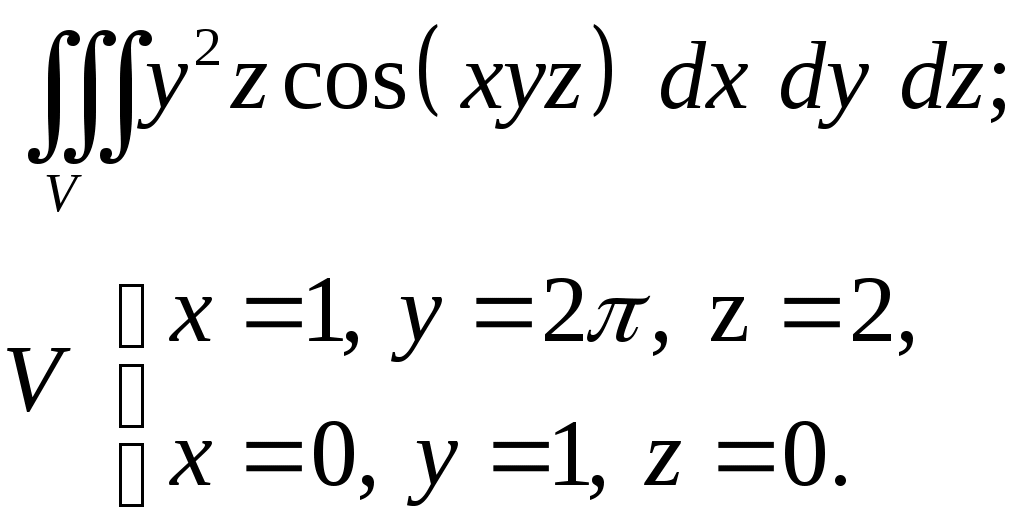 4.7. 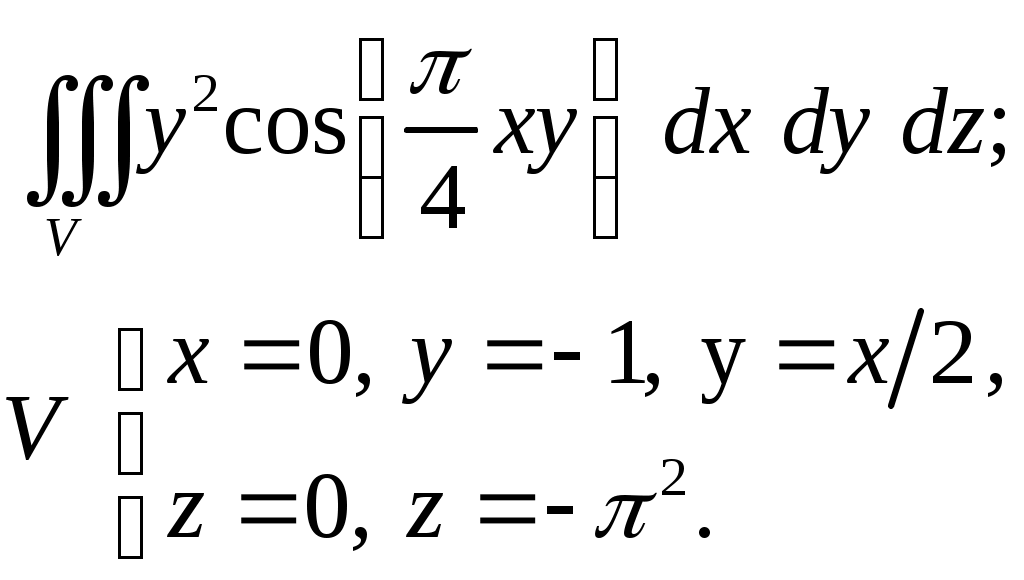 4.8. 4.8. 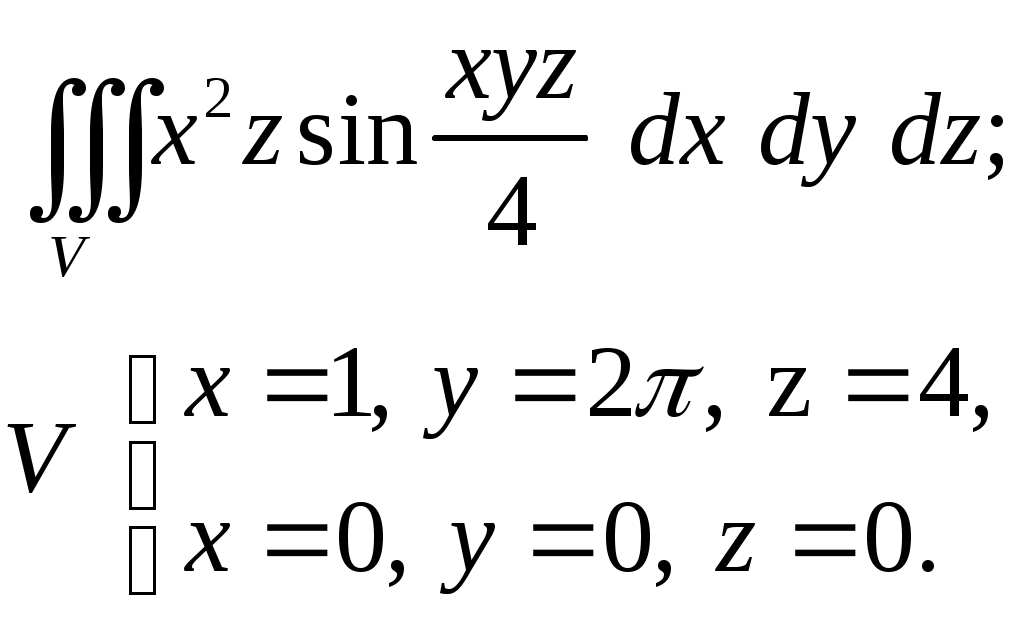 4.9. 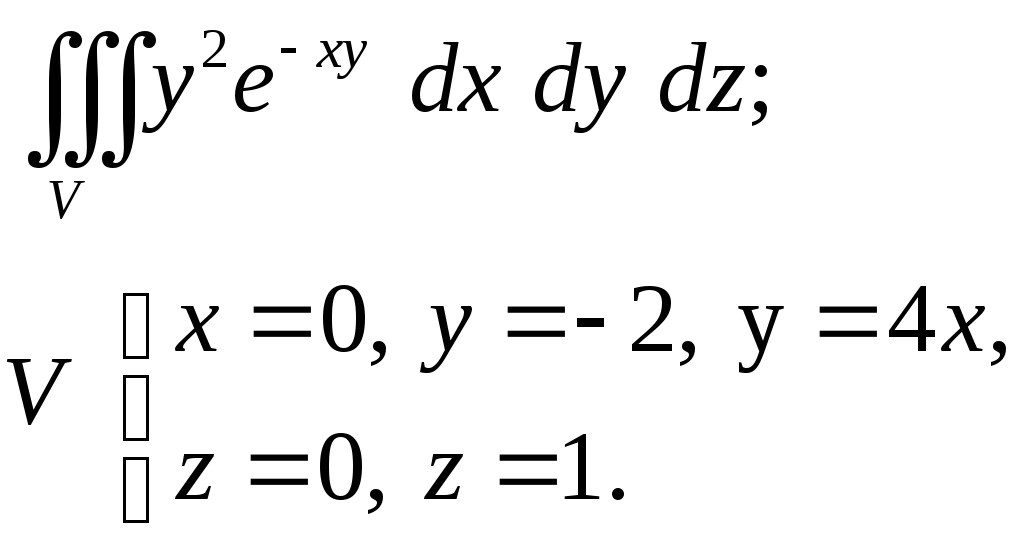 4.10. 4.10. 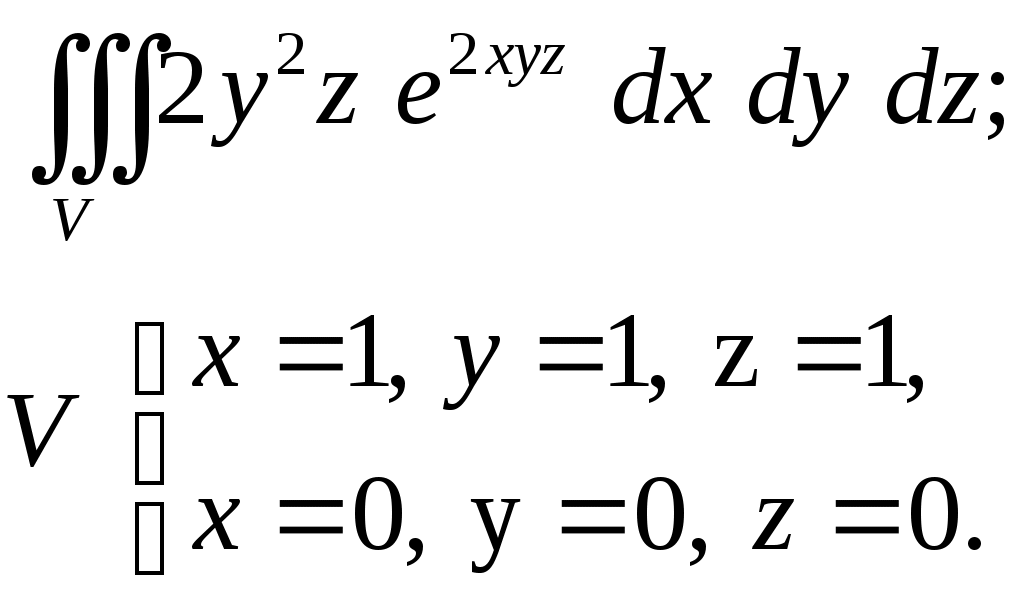 4.11. 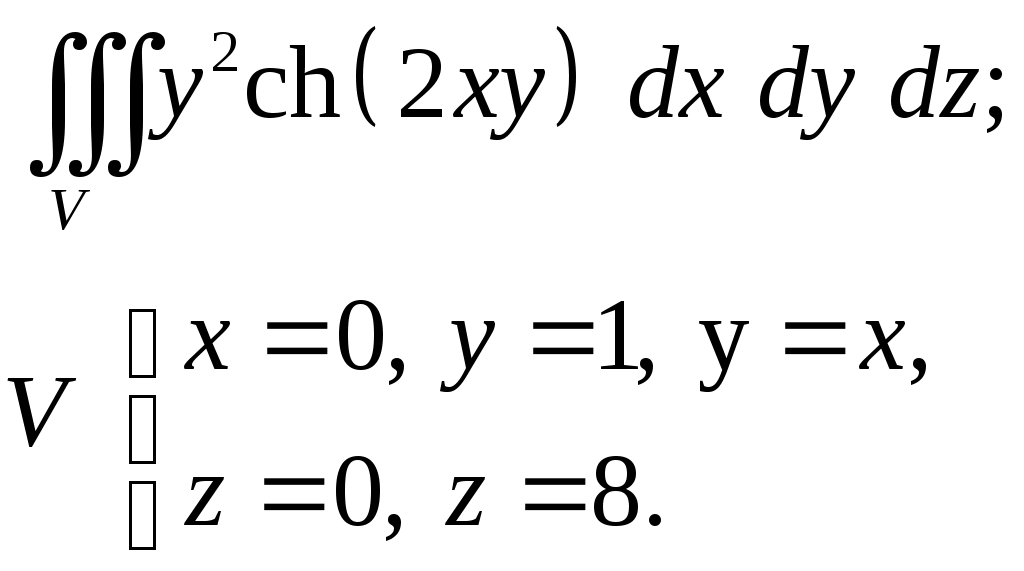 4.12. 4.12. 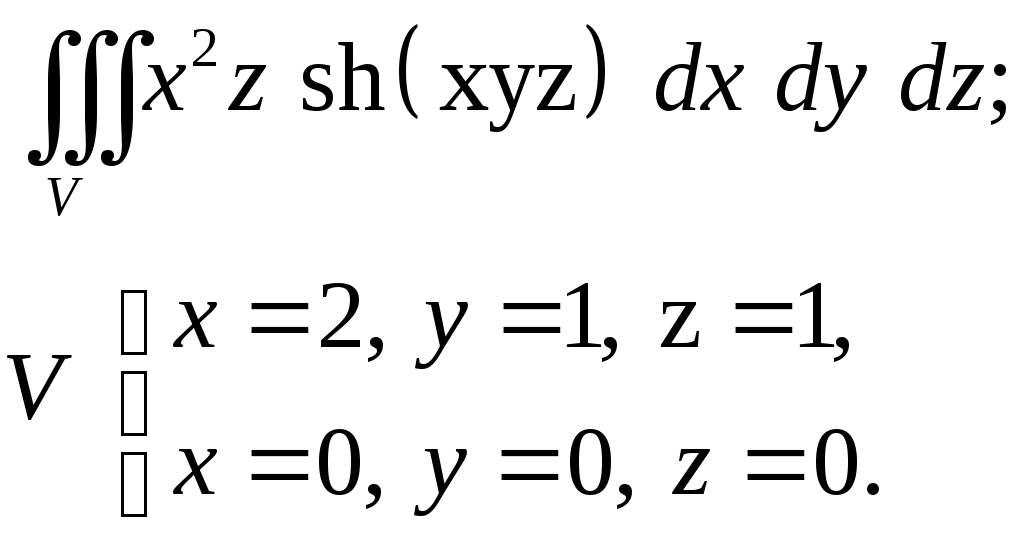 4.13. 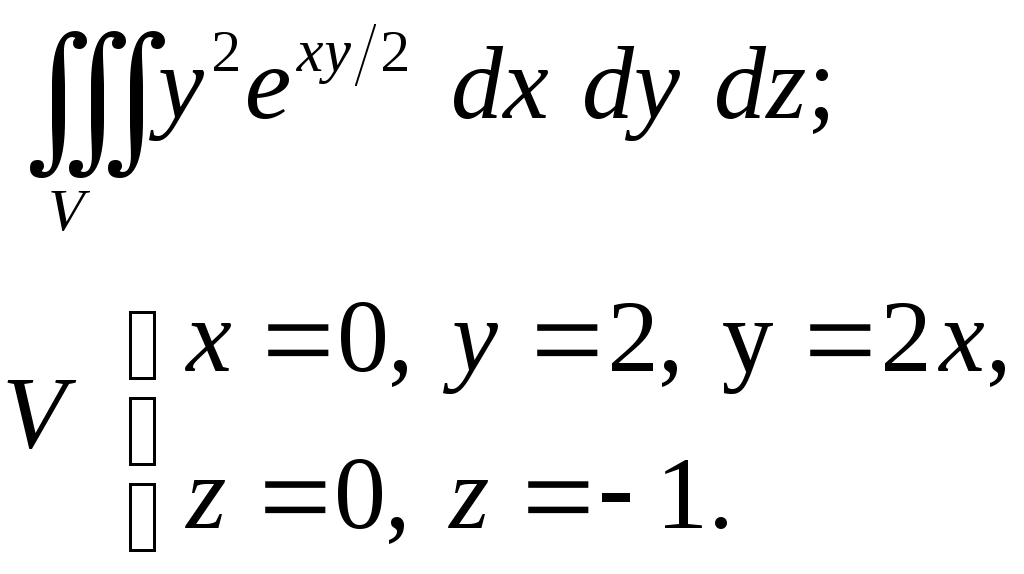 4.14. 4.14. 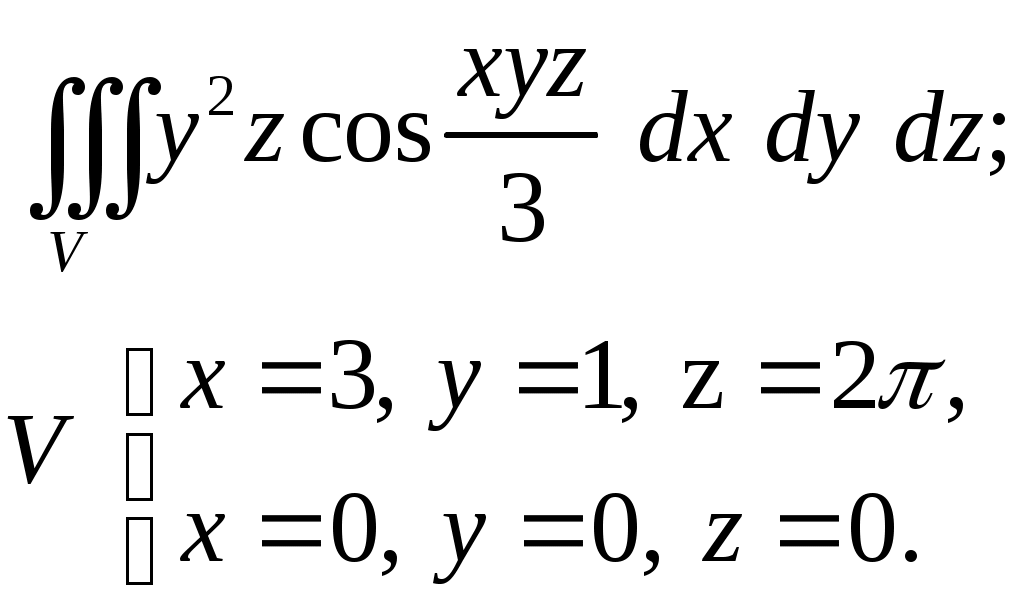 4.15. 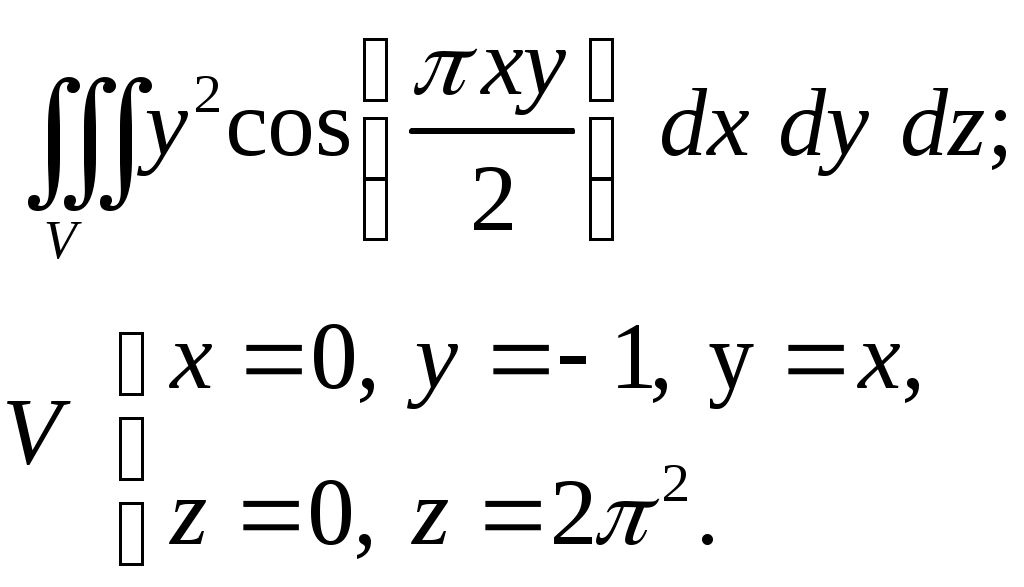 4.16. 4.16. 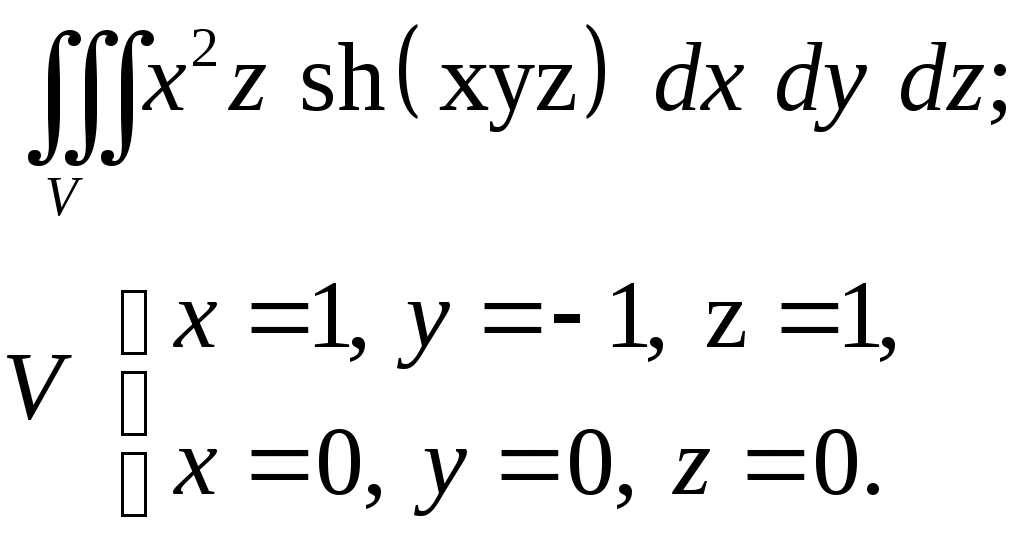 4.17. 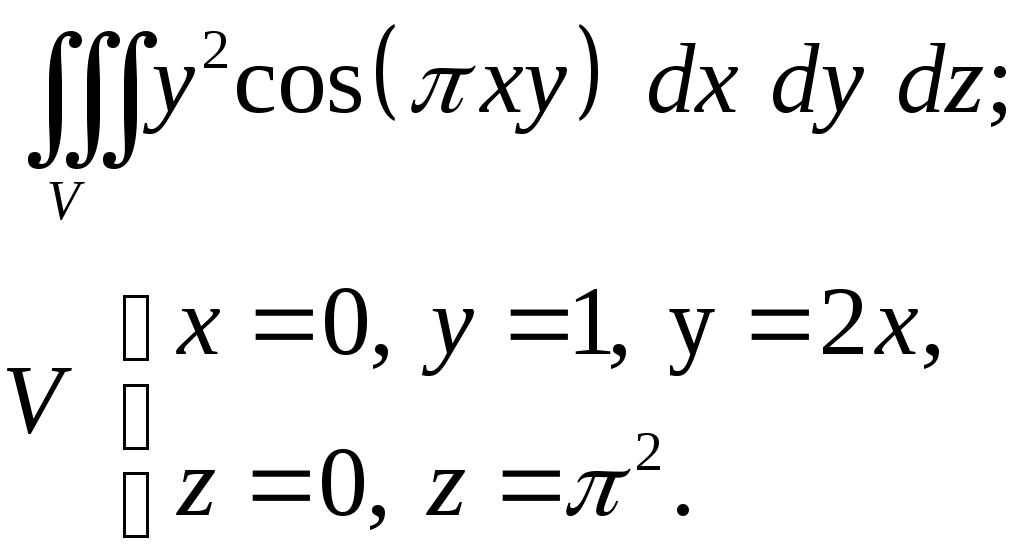 4.18. 4.18. 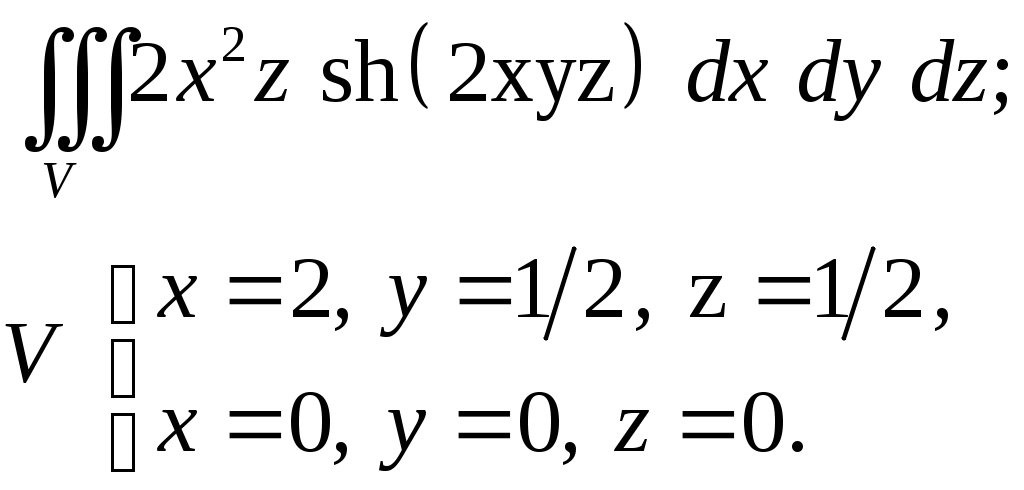 4.19. 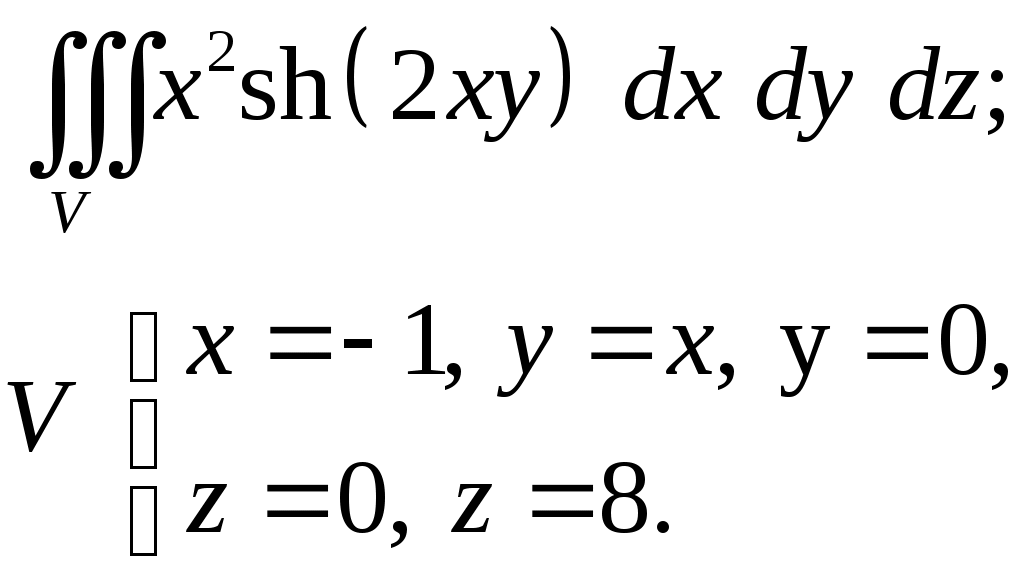 4.20. 4.20. 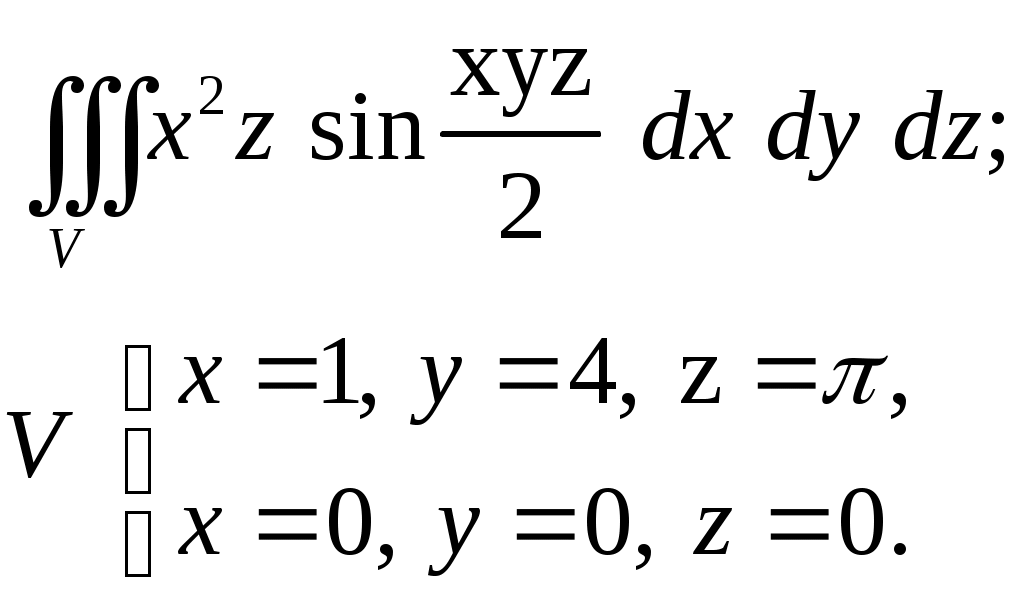 4.21. 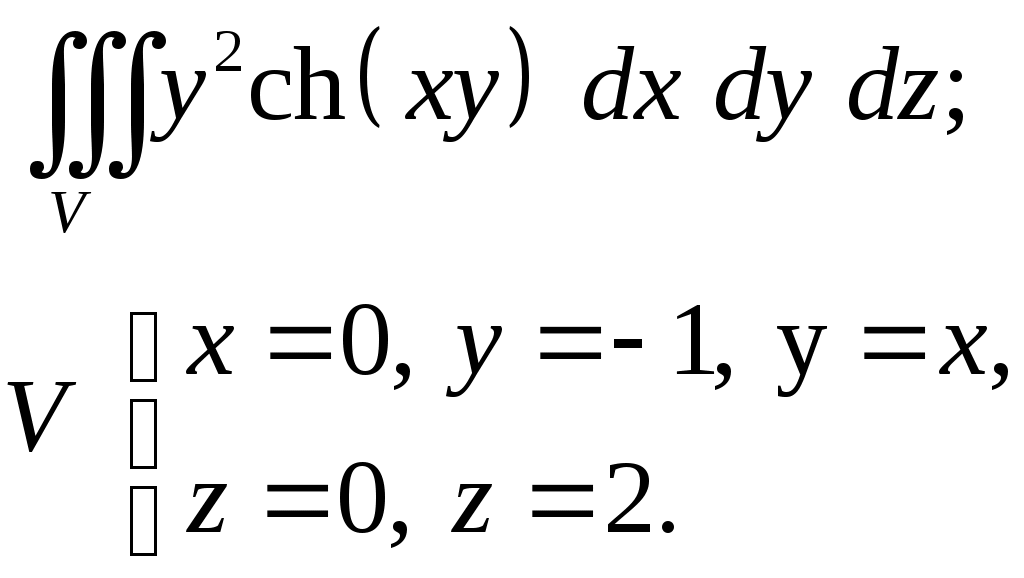 4.22. 4.22. 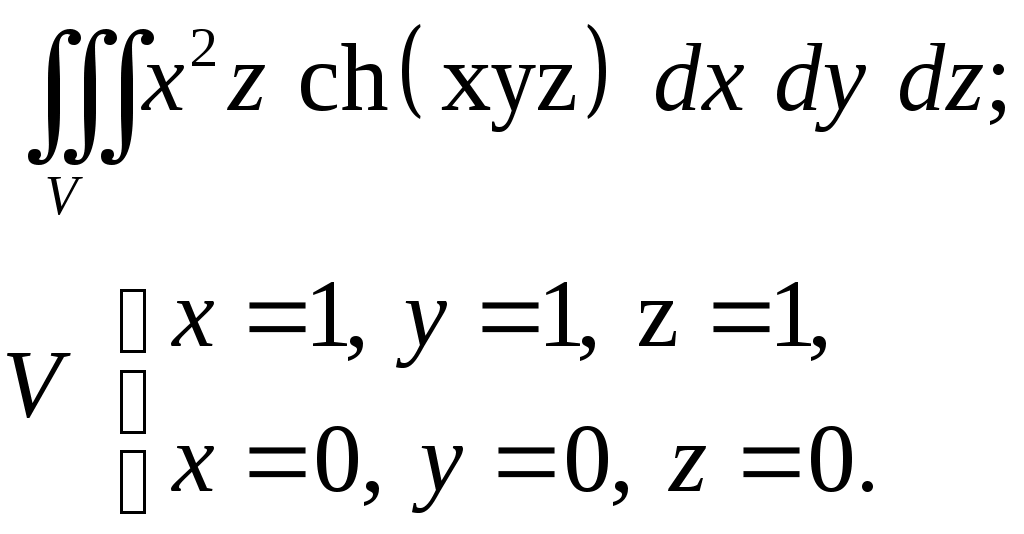 4.23. 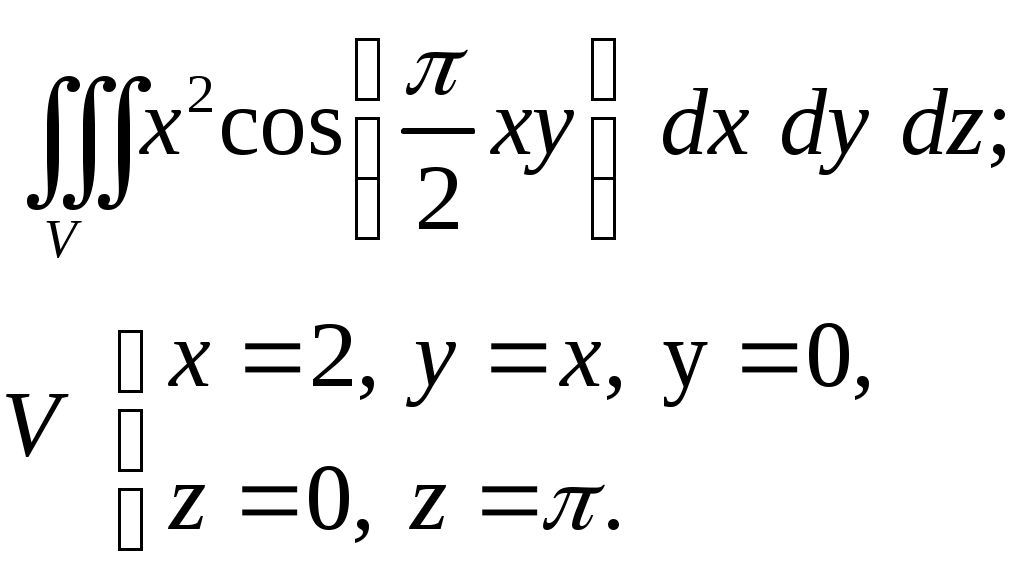 4.24. 4.24. 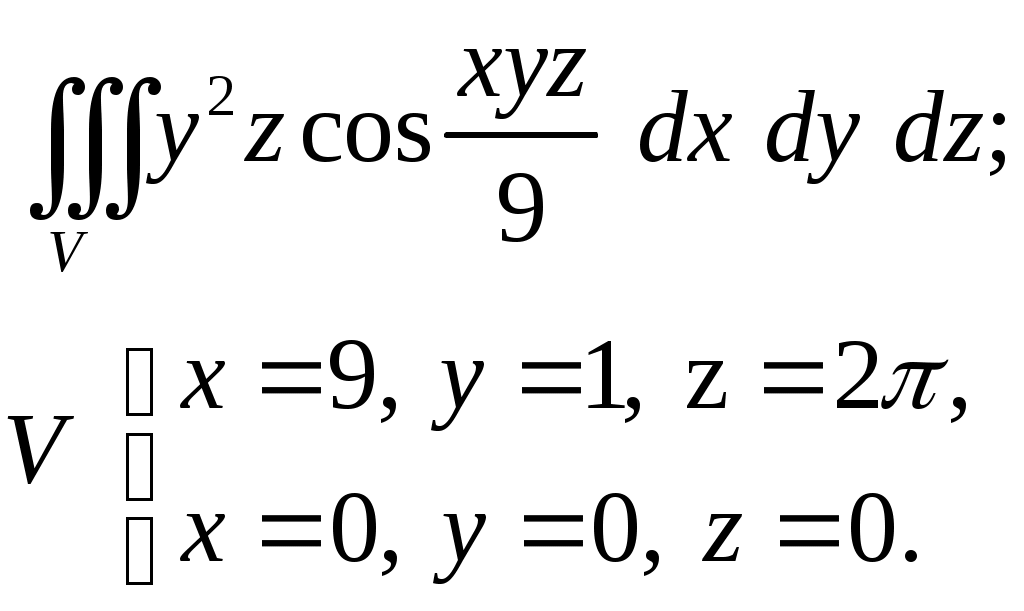 4.25. 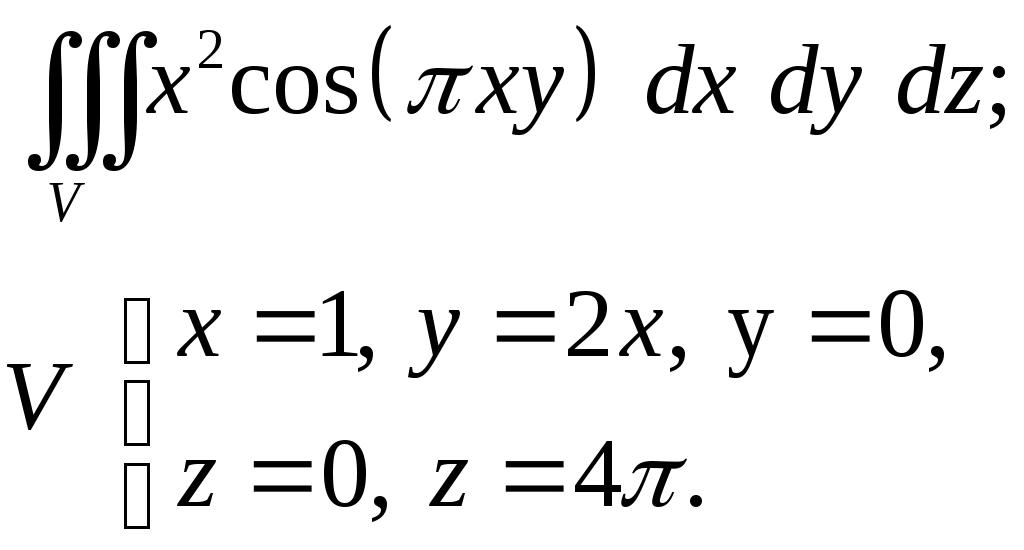 4.26. 4.26. 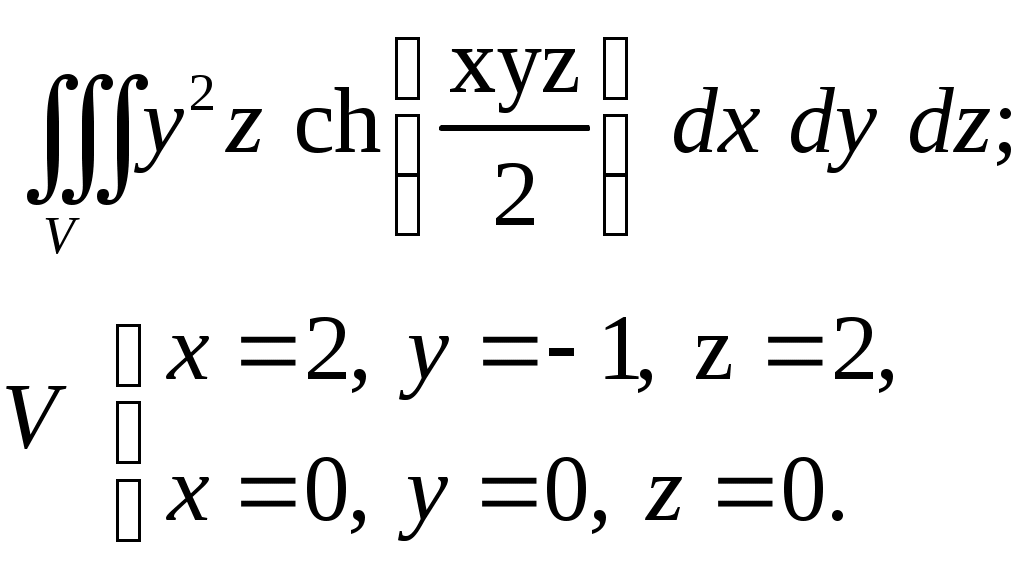 4.27. 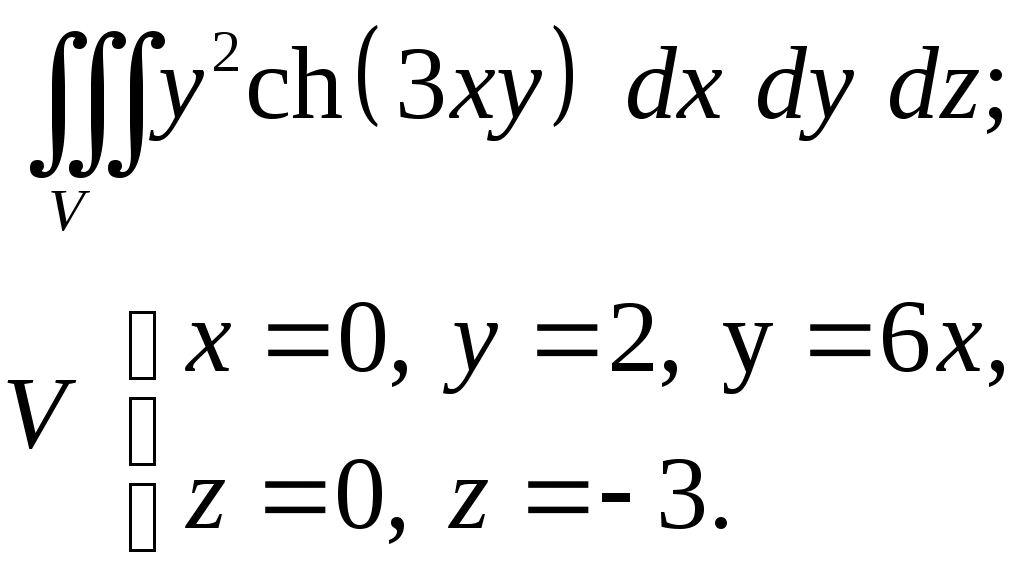 4.28. 4.28. 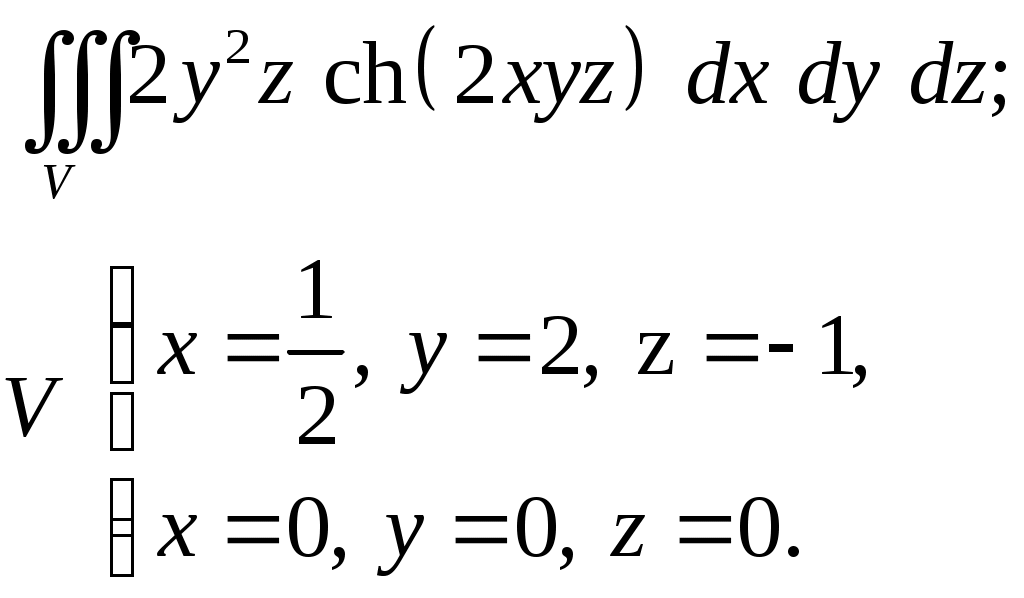 4.29. 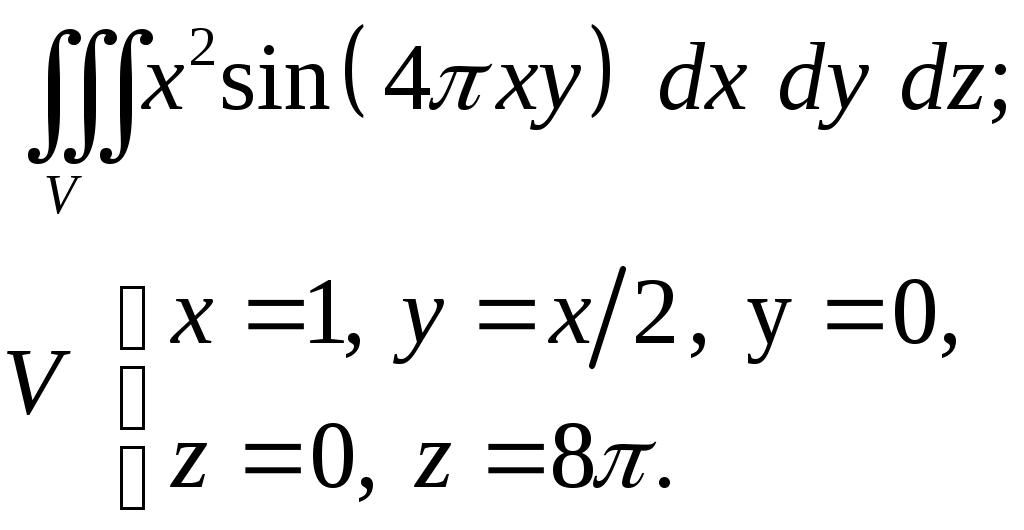 4.30. 4.30. 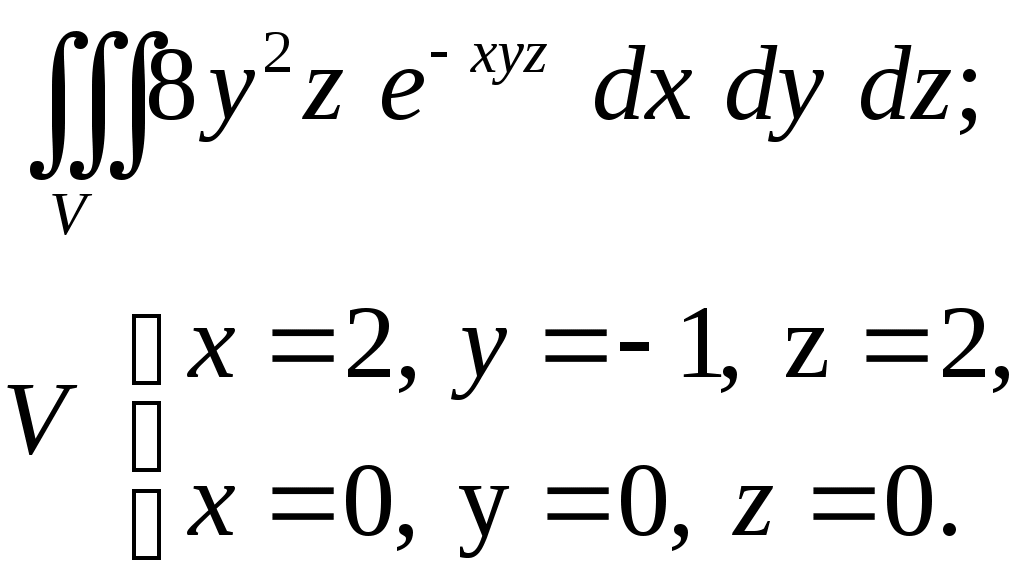 4.31. 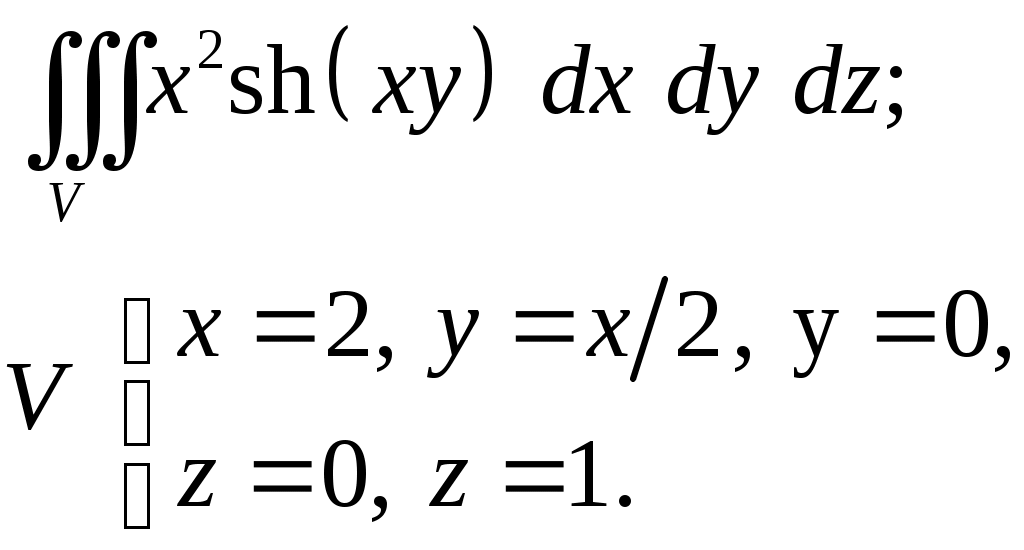 |
