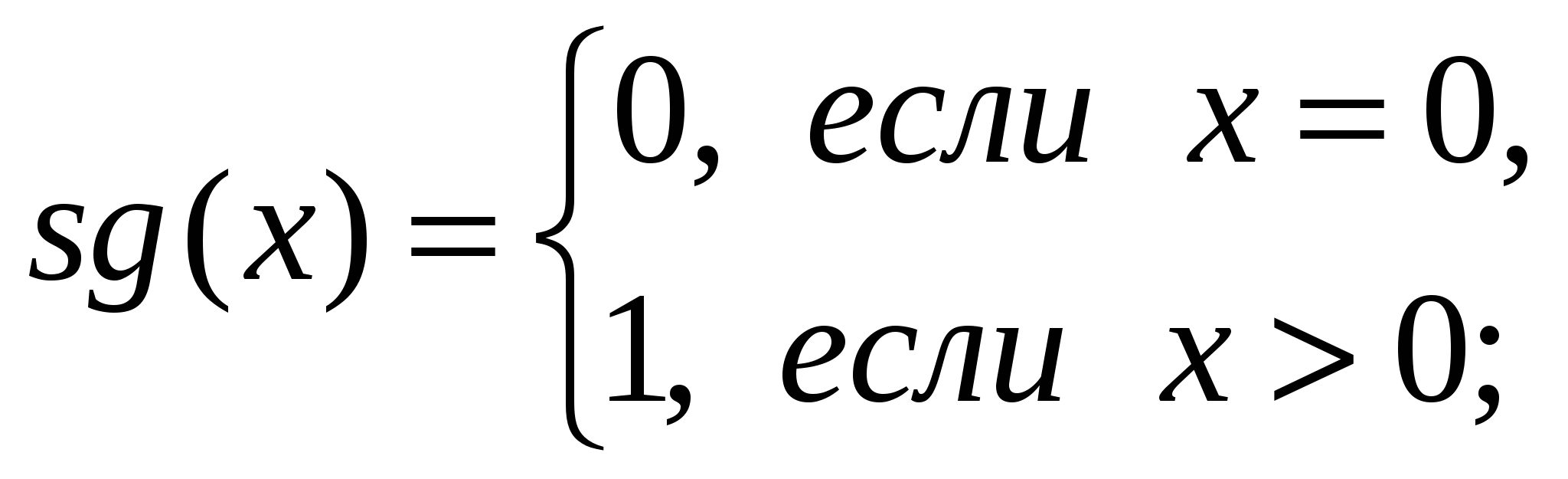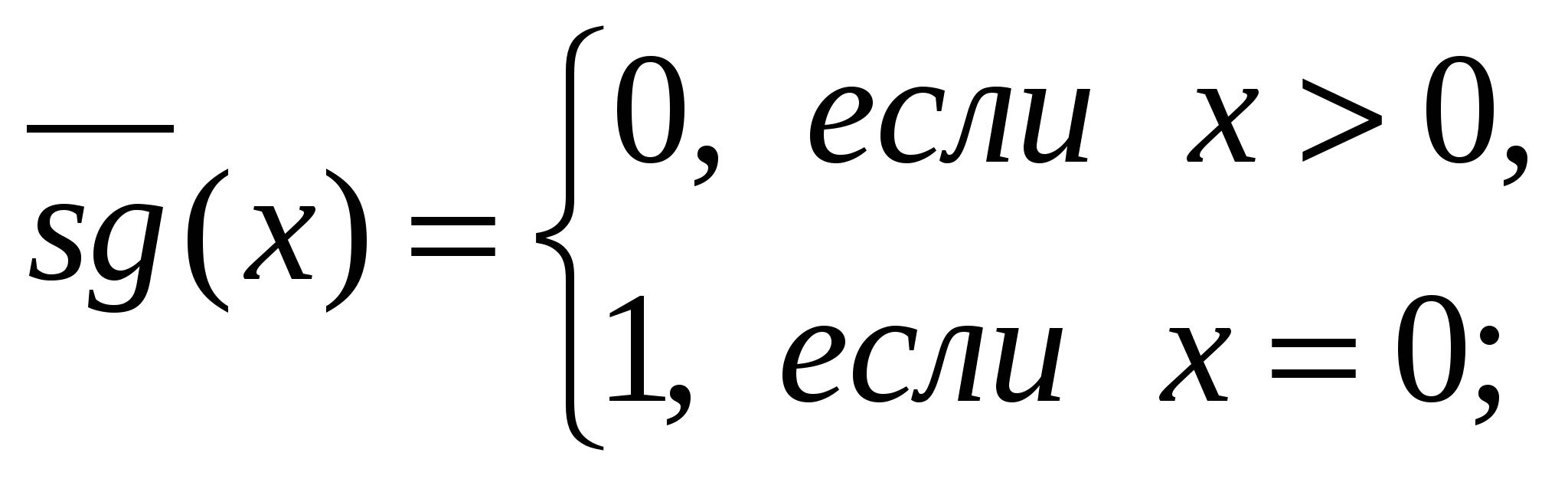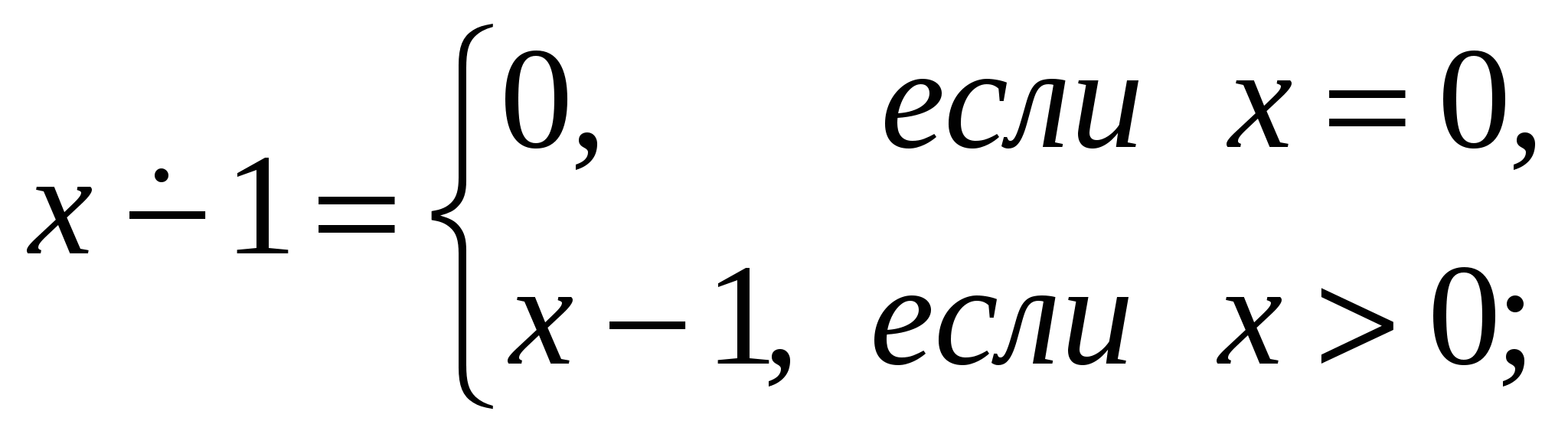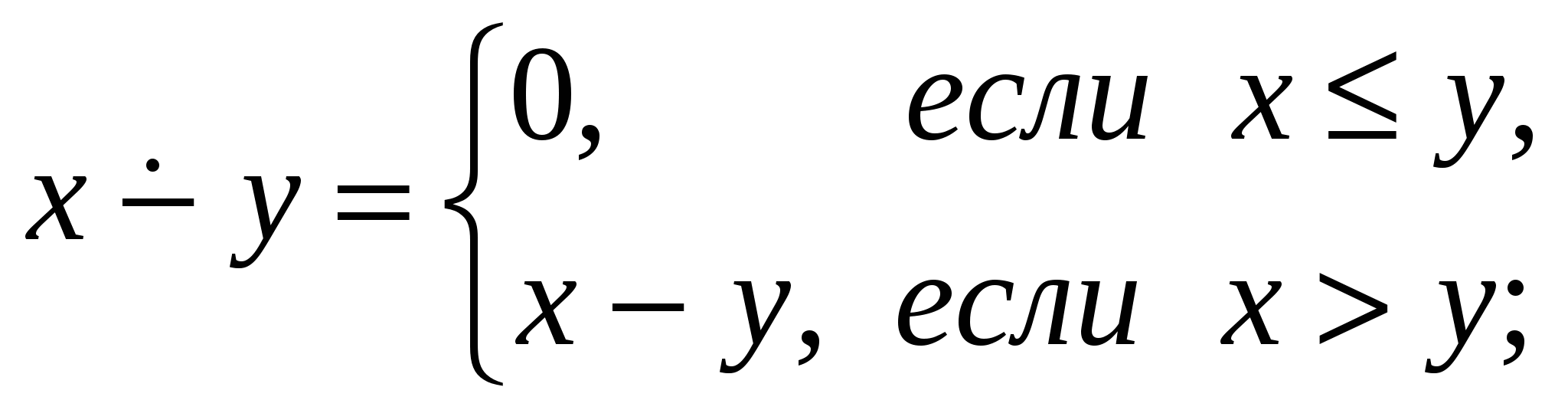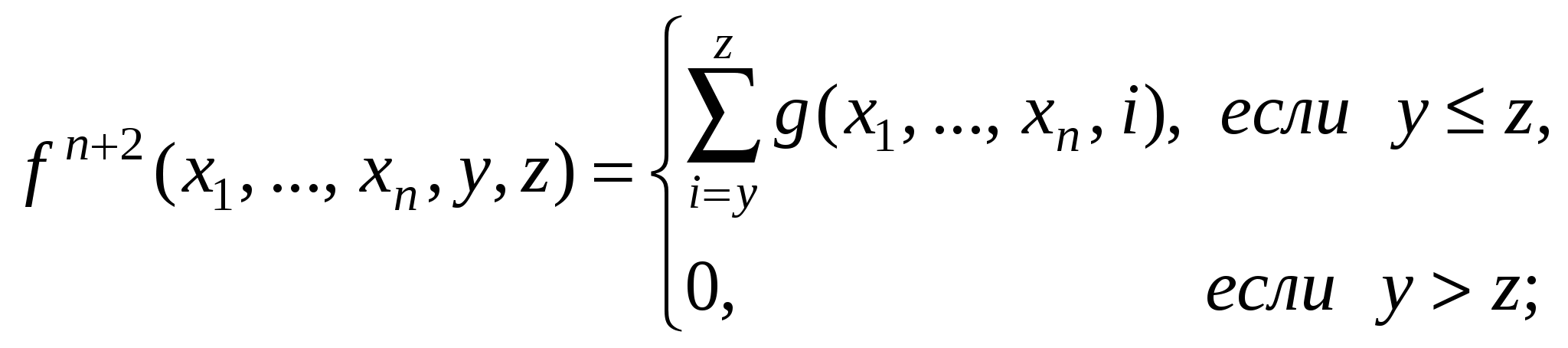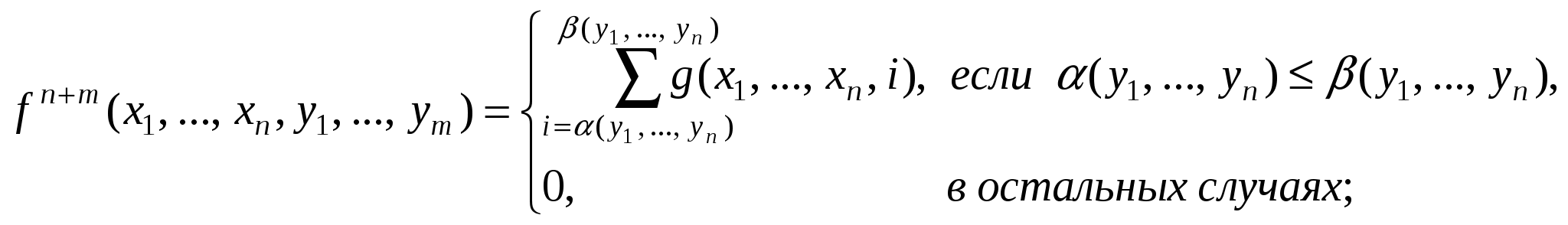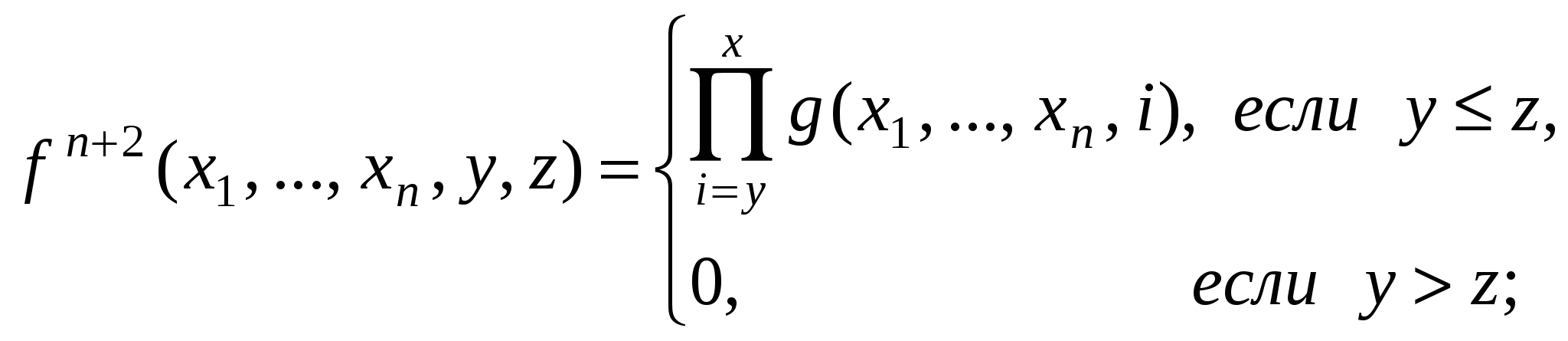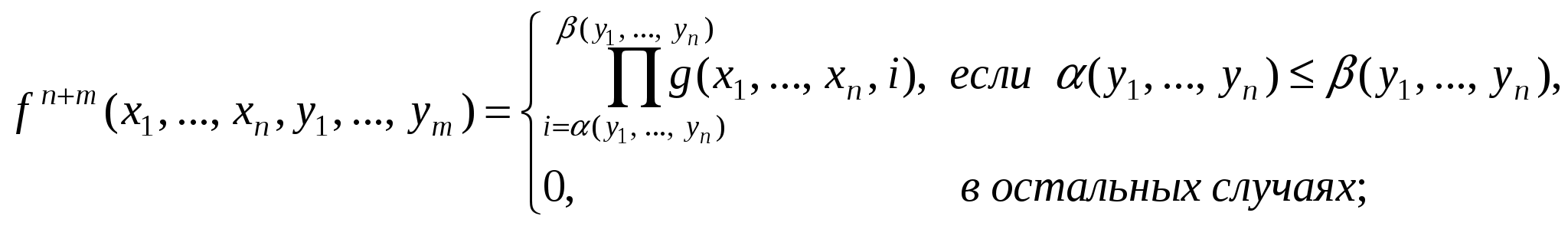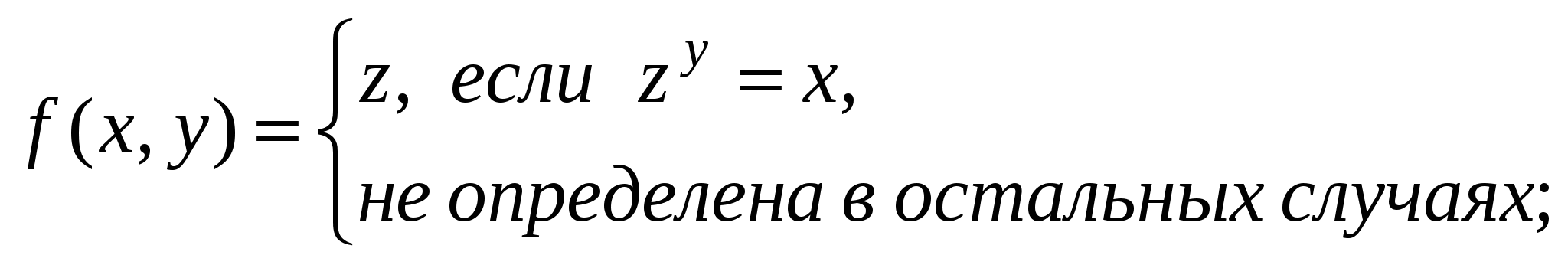Матеем)). Теория множеств определения Множество A
 Скачать 281 Kb.
|
|
ТЕОРИЯ МНОЖЕСТВ Определения
- объединение множеств A и B: = { x : x или xB} - пересечение множеств A и B: = { x : x и xB} - разность множеств A и B: \ B = { x : x и xB } - симметрическая разность множеств A и B: B = (A \ B)(B \ A) - дополнение множества A относительно U, AU:  = U \ AСледует обратить внимание: 1. При доказательстве включения AB использовать следующую схему доказательства: «Пусть x, тогда ..., значит xB. Следовательно, AB.» либо использовать элементарные соотношения типа: (1) A, B (2) A AB, B AB (3) A \ B (4) A B и B C A C и т.д. 2. При доказательстве равенства двух множеств нужно проверять два включения (см. определение равенства). 3. Правильно пользоваться отрицанием условий: x x и xB x x или xB x \ B x или xB Примеры решения задач 1. Доказать равенство множеств: = (B \ A). Решение. Докажем, что (B \ A). Пусть xAB, тогда xA или xВ. Если xA, то по формуле (2) x(B \ A). Если xA и xВ, то по определению разности множеств x(B \ A). По формуле (2) x(B \ A). Докажем, что (B \ A). Пусть x(B \ A), тогда xA или x(B \ A). Если xA, то по формуле (2) xB. Если x(B \ A), то по определению разности множеств xBи xA. Так как xB, то по формуле (2) xB. 2. Доказать: ABC AB и AC Решение. Докажем, что ABC AB и AC. Способ 1. Чтобы доказать, что AB и AC, возьмем x. Так как ABC, то из x следует, что xB и xC. Значит, одновременно выполняются (x и xB) и (x и xC). Поэтому AB и AC. Способ 2. Учитывая соотношение (1) имеем: ABCB и ABCС. Отсюда по транзитивности получаем: AB и AC. Докажем, что ABC AB и AC. Чтобы доказать, что ABC, возьмем x. Так как AB и AC, то из x следует, что xB и xC. По определению пересечения множеств получаем, что x BC. 3. Существуют ли такие множества А, В и С, что , С = , ()\С=? Если существуют, то привести пример. Если не существуют, то доказать это. Решение. Докажем от противного, что таких множеств не существует. Предположим, что существуют множества А, В и С, удовлетворяющие условию задачи. Так как , то существует x, то есть x и xB. Поскольку x и по условию С = , то xС. Так как xС и x, то по определению разности множеств x()\С. Значит, ()\С , что противоречит условию задачи. Следовательно, таких множеств не существует. 4. Доказать равенство множеств А \ (А \ В) = АВ. Решение. xА \ (А \ В) xА и x А \ В xА и (xА или xВ) xА и xВ xАВ. Задачи для самостоятельного решения:
(a)  = .(b)  = .ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ Определения
Пример 1. Пусть A={1, 2, 3}, B={a, b}. Тогда декартовы произведения: AB = { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) }, BA = { (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) }. Видно, что AB BA. Мощности: |AB| = |BA| = 32=6. Пример 2. Пусть A=[-1, 2], B=[1, 3] – отрезки прямых. Тогда декартово произведение AB – это все точки (пары координат) прямоугольника: 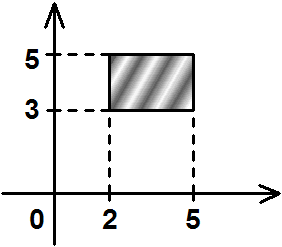 Примеры решения задач 1. Доказать равенство множеств: (B)С=(AC) (BC) Решение. Докажем, что (B)С(AC) (BC). Пусть z(AB)С, тогда z=(x, y), где xAB и yС. Значит, xA или xВ. То есть xA и yС или xВ и yС. Поэтому zAC или zBC. По определению объединения z(AC) (BC). Докажем, что (B)С (AC) (BC). Пусть z(AC)(BC), тогда zAC или zBC. Так как z=(x, y), то xA, yС или xB, yС. Значит, xA или xВ при yС. Поэтому xAB и yС. По определению декартова произведения z(B)С. БИНАРНЫЕ ОТНОШЕНИЯ, ФУНКЦИИ, ПОРЯДОК. Определения
а) f =А, f В б) для всех x, y1, y2 из того, что (x, y1)f и (x, y2)f следует y1=y2.
- рефлексивность: (x, x)R для всех xA. - иррефлексивность: (x, x)R для всех xA. - симметричность: (x, y)R (y, x)R. - антисимметричность: (x, y)R и (y, x)R x=y. - транзитивность: (x, y)R и (y, z)R (x, z)R. - дихотомия: либо (x, y)R, либо (y, x)R для всех xA и yA.
Подмножества Аi , i =1, ..., r, называются блоками разбиения.
Пример 1. Пусть A={1, 2, 3}, B={a, b}. Выпишем декартово произведение: AB = { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) }. Возьмём любое подмножество этого декартова произведения: R ={ (1, a), (1, b), (2, b) }. Тогда R – это бинарное отношение на множествах Aи B. Будет ли это отношение являться функцией? Проверим выполнение двух условий 9a) и 9б). Область определения отношения R – это множество R ={1, 2}{1,2,3}, то есть первое условие не выполняется, поэтому в R нужно добавить одну из пар: (3, a) или (3, b). Если добавить обе пары, то не будет выполняться второе условие, так как ab. По этой же причине из R нужно выбросить одну из пар: (1, a) или (1, b). Таким образом, отношение R={ (1, a), (2, b), (3, b) } является функцией. Заметим, что R не является 1-1 функцией. На заданных множествах A и В функциями также будут являться следующие отношения: { (1, a), (2, a), (3, a) }, { (1, a), (2, a), (3, b) }, { (1, b), (2, b), (3, b) } и т.д. Пример 2. Пусть A={1, 2, 3}. Примером отношения на множестве A является R = {(1,1),(2,1), (2, 3) }. Примером функции на множестве A является f = {(1,1),(2,1), (3, 3) }. Примеры решения задач 1. Найти R, R, R1, RR, RR1, R1R для R = {(x, y) | x, y D и x+y0}. Решение. Е  сли (x, y)R, то x и y пробегают все действительные числа. Поэтому R = R = D. Если (x, y)R, то x+y0, значит y+x0 и (y, x)R. Поэтому R1=R. Для любых xD, yD возьмём z=-|max(x, y)|-1, тогда x+z0 и z+y0, т.е. (x, z)R и (z, y)R. Поэтому RR = RR1 = R1R = D2. 2. Для каких бинарных отношений R справедливо R1= R? Решение. Пусть RAB. Возможны два случая:
Поэтому если A и B, то таких отношений R не существует. 3. На множестве D действительных чисел определим отношение R следующим образом: (x, y)R (x–y) – рациональное число. Доказать, что R есть эквивалентность. Решение. Рефлексивность: Для любого xD x-x=0 – рациональное число. Потому (x, x)R. Симметричность: Если (x, y)R, то x-y =  . Тогда y-x=-(x-y)=- – рациональное число. Поэтому (y, x)R.Транзитивность: Если (x, y)R, (y, z)R, то x-y = и y-z = . Складывая эти два уравнения, получаем, что x-z = + – рациональное число. Поэтому (x, z)R.Следовательно, R – это эквивалентность. 4. Разбиение плоскости D2 состоит из блоков, изображённых на рисунке а). Выписать отношение эквивалентности R, соответствующее этому разбиению, и классы эквивалентности. Аналогичная задача для b) и c). 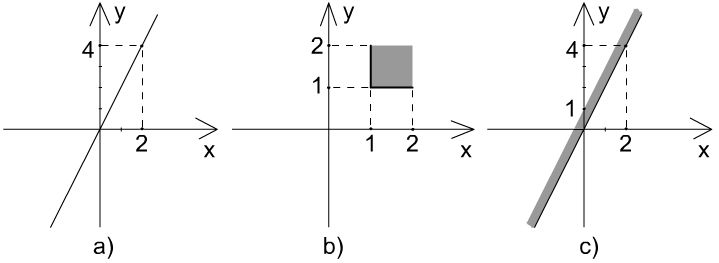 Решение. а) две точки эквивалентны, если лежат на прямой вида y=2x+b, где b – любое действительное число. b) две точки (x1,y1) и (x2,y2) эквивалентны, если (целая часть x1 равна целой части x2) и (целая часть y1 равна целой части y2). с) решить самостоятельно. Задачи для самостоятельного решения: 1. Доказать, что если f есть функция из A в B и g есть функция из B в C, то fg есть функция из A в C. 2. Пусть A и B – конечные множества, состоящие из m и n элементов соответственно.
3. Доказать, что f удовлетворяет условию f(AB)=f(A)f(B) для любых A и B тогда и только тогда, когда f есть 1-1 функция. КОМБИНАТОРИКА Произведение всех натуральных чисел от 1 до n обозначается: n! = 1·2·3·…·(n-1)·n, 0! = 1 Пусть X={x1, x2, ..., xn} – это множество из n элементов, k n. Размещение элементов из X объёма k – это упорядоченное подмножество из k элементов, принадлежащих X. Количество размещений объёма k из n различных элементов с неограниченными повторениями:  = nk (значмест)Если на каждую i-ю из k позиций можно поставить один из qi элементов множества X, то количество таких размещений равно: (q1, q2, ..., qn) = q1 q2 ... qnКоличество размещений объёма k из n различных элементов без повторений:  =n(n - 1)(n - 2) … (n - k + 1)=  Перестановка элементов из X – это размещение элементов из X объёма n. Количество перестановок из n различных элементов:  = Pn = n!Если n элементов содержат qi элементов i-го сорта, q1+ q2+...+ qm= n и элементы одного сорта идентичны, то число перестановок равно: Pn(q1, q2, ..., qm) =  Сочетание элементов из X объёма k – это неупорядоченное подмножество из k элементов, принадлежащих X. Сочетания, размещения и перестановки могут быть также с повторениями элементов множества X (неограниченными и ограниченными). Количество сочетаний объёма k из n различных элементов без повторений:  Количество сочетаний объёма k из n различных элементов с неограниченными повторениями:  Бином Ньютона:  Свойства: (1)  (2)  (3)  (4)  (5) При решении комбинаторных задач часто используются следующие правила комбинаторики:
Задача-пример. Из 12 девушек и 10 юношей выбирают команду, состоящую из пяти человек. Сколькими способами можно выбрать эту команду так, чтобы в нее вошло не более трех юношей? Решение. Условие «не более трех» означает, что в команду может входить либо 3 юноши, либо 2 юноши, либо 1 юноша, либо ни одного юноши. Таким образом, в задаче выделяются четыре различных случая. В соответствии с правилом сложения нужно подсчитать количества вариантов в каждом из этих случаев и сложить их. Рассмотрим первый случай. Нужно подсчитать, сколькими способами можно выбрать из 12 девушек и 10 юношей команду, состоящую из 3х юношей и 2х девушек. Из 10 юношей можно выбрать 3х юношей  способами. Для каждых трех выбранных юношей можно выбрать также  способами 2х девушек из 12ти. Поэтому работает правило умножения и в первом случае число вариантов команд равно .Аналогично, во втором случае:   .В третьем случае:   .В четвертом случае:  .Окончательный ответ: +++.Примеры решения задач №1.17. n (n>2) человек садятся за круглый стол. Два размещения по местам будем считать совпадающим, если каждый человек имеет одних и тех же соседей в обоих случаях. Сколько существует способов сесть за стол? Решение. Общее количество всевозможных рассадок равно числу перестановок из n элементов Pn = n! Однако из этих рассадок нужно исключить совпадающие. Отношение соседства сохраняется при циклических перестановках (их n штук) и при симметрическом отражении (их также n штук): 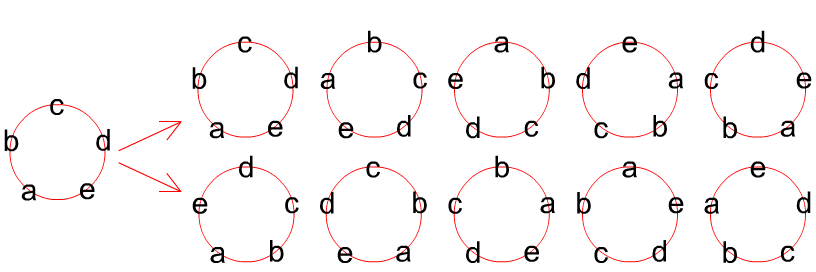 Поэтому всего способов  (делить, т.к. правило умножения) №1.19. Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется хотя бы один туз? Решение. Всего способов вынуть 10 карт из колоды  . Из них в  случаях в выборке не окажется ни одного туза. Поэтому ответ –.№1.20. Сколькими способами можно составить три пары из n шахматистов? Решение. Сначала выберем из n шахматистов 6 человек. Это можно сделать  способами. Теперь каждую шестёрку будем разбивать на пары. Для этого поставим 6 шахматистов в ряд, считая, что они имеют имена: a, b, c, d, e, f. Это можно сделать 6! способами. Однако нам не важен порядок внутри каждой пары и порядок самих пар. Перестановок, в которых шахматисты меняются местами в парах 23. Перестановок, в которых меняются местами пары 3!. Поэтому разбить на пары 6 шахматистов можно  способами. Ответ .№1.24. Сколько существует чисел от 0 до 10n, в которые не входят две идущие друг за другом одинаковые цифры? Решение. Рассмотрим все n-значные числа. Первую цифру мы можем выбрать 9-ю способами. Чтобы вторая цифра была отлична от первой, то её также можно выбрать 9-ю способами. Количество таких n-значных чисел равно количеству размещений объёма n из 9 элементов с неограниченными повторениями, т.е. равна 9n для n>1 и 10 для n=1. Поэтому ответ 10+92+93+...+9n. Число 10n не подходит. ТЕОРИЯ АЛГОРИТМОВ
1. s(x)=x+1 для любого x; 2. o(x)=0 для любого x; 3. Inm(x1, ..., xm, ..., xn)=xm. Эти простейшие функции всюду определены и из них с помощью конечного числа применений операторов, введенных ниже, можно конструировать более сложные функции.
Функция hn(x1, ..., xn) получается из функций gm, fn1, ..., fnm с помощью оператора суперпозиции, если hn(x1, ..., xn) = gm(fn1(x1, ..., xn), ..., fnm(x1, ..., xn)).
Функция fn+1(x1, ..., xn, y) получается из функций gn(x1, ..., xn) и hn+2(x1, ..., xn, y, z) с помощью оператора примитивной рекурсии, если она может быть задана схемой примитивной рекурсии: fn+1(x1, ..., xn, 0) = gn(x1, ..., xn), fn+1(x1, ..., xn, y+1) = hn+2(x1, ..., xn, y, fn+1(x1, ..., xn, y)).
Функция fn(x1, ..., xn) получается из функции gn+1(x1, ..., xn, y) с помощью оператора минимизации и обозначается fn(x1, ..., xn)=y[gn+1(x1, ..., xn, y)=0], если: fn(x1, ..., xn) определено и равно y gn+1(x1, ..., xn, 0), ..., gn+1(x1, ..., xn, y-1) определены и не равны нулю, а gn+1(x1, ..., xn, y)=0. (Можно говорить также: «Функция fn(x1, ..., xn) равна минимальному значению y, при котором функция gn+1 обращается в нуль»)
Функция fn+1(x1, ..., xn, y) называется примитивно рекурсивной, если она может быть получена из простейших функций с помощью конечного числа применений операторов суперпозиции и примитивной рекурсии. Следует отметить, что все примитивно рекурсивные функции всюду определены.
Функция fn+1(x1, ..., xn, y) называется частично рекурсивной, если она может быть получена из простейших функций с помощью конечного числа применений операторов суперпозиции, примитивной рекурсии и минимизации.
Примеры решения задач 1. Доказать, что следующие функции являются примитивно рекурсивными. a) f(x)=x+n Решение. Функция f(x) может быть получена с помощью n-кратного применения оператора суперпозиции к простейшей функции s(x). b) f(x,y)=x+y Решение. Функция f(x) может быть задана следующей схемой примитивной рекурсии: f(x, 0) = x = I11(x), f(x, y+1) = x+y+1=f(x,y)+1=s(f(x,y))=s(I33(x,y,f(x,y))). Здесь функция g(x) имеет вид g(x)= I11(x) и является, как и полагается, функцией одной переменной. А функция h(x,y,z) имеет вид h(x,y,z)=s(I33(x,y,z)) и является функцией трех переменных. Заметим, что функции g(x) и h(x,y,z) являются прф, т.к. g(x) – третья простейшая функция, а h(x,y,z) может быть получена из простейших функций s(x) и I33(x,y,z) с помощью применения оператора суперпозиции. Так как функцию f(x,y) можно получить с помощью оператора примитивной рекурсии из примитивно рекурсивных функций g(x) и h(x,y,z), то f(x,y) – прф. с) f(x,y)=xy Решение. Функция f(x) может быть задана следующей схемой примитивной рекурсии: f(x, 0) = 0 = o(x), f(x, y+1) = x(y+1)=xy+x=f(x,y)+x= I33(x,y,f(x,y)))+ I31(x,y,f(x,y))). Так как функцию f(x,y) можно получить с помощью оператора примитивной рекурсии из примитивно рекурсивных функций g(x)=o(x) и h(x,y,z) = I33(x,y,z)) + I31(x,y,z)), то f(x,y) – прф. 2. Пусть g(x1, ..., xn,y) примитивно рекурсивная функция. Доказать, что следующая функция примитивно рекурсивна:  Решение. Особенность этой функции заключается в том, что суммирование ведется по переменному числу слагаемых. Однако функция fn+1 может быть задана следующей схемой примитивной рекурсии: f(x1, ..., xn, 0) = g(x1, ..., xn,0) – прф, f(x1, ..., xn, y+1) =  = f(x1, ..., xn, y) + g(x1, ..., xn,y+1) – сумма прф g и самой функции f.3. Доказать, что следующая функция частично рекурсивна. 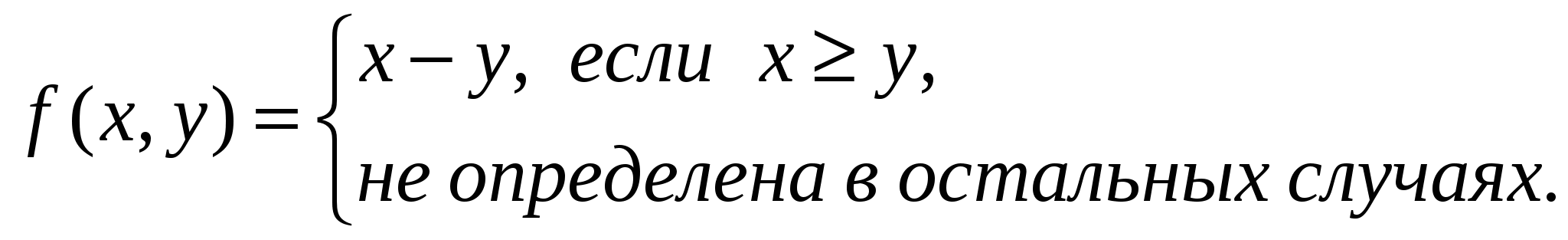 Решение. Покажем, что функция f(x,y) может быть получена с помощью оператора минимизации. Пусть xy, тогда f(x,y) определена и принимает некоторое значение: f(x,y) = xy = z. Как вычислить z? Можно предложить следующий способ: начиная с нуля перебирать по порядку все значения z, пока не выполнится условие xy=z, или xyz=0. Такое z обязательно найдется, т.к. xy0. Если же xy<0, то ни какое натуральное z не подойдет. Программист записал бы это так: unsigned int f(x,y) { z=0; while((xyz)!=0) z++; return z; } То же самое можно записать и в терминах оператора минимизации: f(x, y)=z[|x–y–z|=0] Модуль необходим для того, чтобы функция g(x,y,z)=|x–y–z| была определена, даже если x–y<0. Заметим, что g(x,y,z)=|x–y–z| является примитивно рекурсивной, т.к. может быть получена с помощью конечного числа применений оператора суперпозиции к простейшим функциям. Поэтому f(x,y) – чрф. Задачи для самостоятельного решения: 1. Доказать, что следующие функции являются примитивно рекурсивными.
2. Пусть gn+1, m, m примитивно рекурсивные функции. Доказать, что следующие функции примитивно рекурсивны: 3. Доказать, что частично рекурсивны следующие функции:
|
