Теория оптимизации

• Название: Теория оптимизации
• Дата: 10.05.2023
• Размер: 260.45 Kb.
• Имя файла: Laboratornyie-rabotyi-1-2-TOiPR.docx
• Тип: Решение; #1120224
• страница: 1 из 6

МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ 1-2
ПО ДИСЦИПЛИНЕ “ТЕОРИЯ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ”

ВВЕДЕНИЕ

Лабораторные работы предполагают решение задач оптимизации с использованием надстройки “Поиск решения” Microsoft EXCEL.
Доступ к инструменту Поиск решения осуществляется с помощью команды Данные Анализ Поиск решения

Если команда Поиск решения или группа Анализ отсутствует на вкладке

Данные, то необходимо загрузить соответствующую надстройку:

1. 
   Выбрать команду Файл Параметры.
   
2. 
   В диалоговом окне Параметры Ехсеl выбрать категорию Надстройки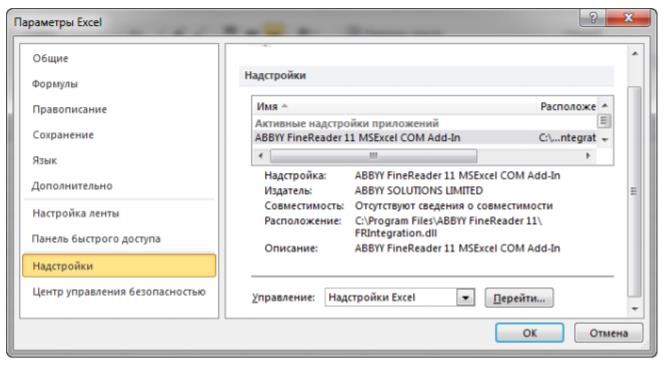
   

3. 
   В поле Управление выбрать значение Надстройки Excel, затем кнопку
   

Перейти.

4. 
   В поле Доступные надстройки установить флажок рядом с пунктом
   

Поиск решения и нажать кнопку ОК.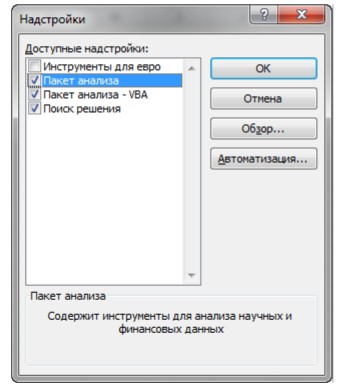

После выполнения этих действий команда Поиск решения будет доступной в группе команд Анализ вкладки Данные.

В методических указаниях подробно рассмотрены основные этапы решения задач с использованием версии Microsoft EXCEL 2007. В других версиях решение осуществляется аналогично.

ЛАБОРАТОРНАЯ РАБОТА №1

РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОЙ ОПТИМИЗАЦИИ СРЕДСТВАМИ EXCEL
Цельработы: Получение практических навыков формирования математических моделей прикладных задач линейного программирования и их решения средствами EXCEL.
Лабораторныезадания.

1. 
   По лекциям и учебному пособию ознакомиться с постановкой и методами решения задач линейной оптимизации (ГЛАВА 3, п. 3.1-3.4.).
   
2. 
   Выбрать задачу в соответствии с вариантом, составить ее математическую модель и решить с использованием средств EXCEL. Сформировать отчеты по устойчивости, результатам и пределам. Для визуализации результатов решения построить диаграммы. Проанализировать полученные результаты.
   
3. 
   Провести параметрический анализ решая задачу при пяти различных значениях ресурса оборудования первого типа (варианты 1-3), второго типа (варианты 4-7) и третьего типа (варианты 8-10).
   

3. 
   Решить задачу вручную с использованием симплекс-метода и графического метода. (Графический метод изложен в п.3.3.1 учебного пособия, симплекс-метод – в п.3.3.2)
   
4. 
   Сравнить результаты, полученные при выполнении лабораторных заданий 1 и 2.
   

Отчетполабораторной работе должен содержать :

1. 
   Постановку задачи.
   
2. 
   Математическую оптимизационную модель.
   
3. 
   Краткое описание основных этапов решения в среде EXCEL.
   
4. 
   Результат решения задачи (итоговую таблицу в EXCEL).
   
5. 
   Отчеты по результатам, устойчивости, пределам.
   
6. 
   Построенные диаграммы.
   
7. 
   Результаты параметрического анализа с соответствующими выводами.
   
8. 
   Решение задачи вручную с использованием симплекс-метода и графического метода.
   
9. 
   Выводы.
   

Для производства двух видов изделий A и B используются три типа технологического оборудования. Для производства одного изделия A оборудование первого типа используется в течение a₁ часов, оборудование второго типа – a₂ часов, оборудование третьего типа – a₃ часов. Для производства одного изделия B оборудование первого типа используется в течение b₁ часов, оборудование второго типа – b₂ часов, оборудование третьего типа – b₃ часов. На изготовление всех изделий предприятие может использовать оборудование

первого типа не более чем t₁ часов, оборудование второго типа – не более t₂ часов, оборудование третьего типа – не более t₃ часов. Прибыль от реализации одного готового изделия A составляет денежных единиц, а изделия В - денежных единиц. Составить план производства изделий A и B, обеспечивающий максимальную прибыль от их реализации.

Вариант	a1	a2	a3	b1	b2	b3	t1	t2	t3		
1	1	1	3	1	2	1	20	36	40	2	5
2	2	1	3	2	2	1	40	34	46	1	2
3	3	1	3	3	2	1	60	32	50	1	3
4	1	1	3	1	2	1	24	40	52	2	4
5	2	1	3	2	2	1	48	38	56	2	6
6	3	2	1	1	2	2	40	40	36	2	1
7	3	1	1	1	2	1	46	34	20	5	2
8	1	3	3	2	3	1	32	60	50	4	2
9	1	3	1	2	1	1	40	52	24	6	2
10	3	2	1	1	2	2	56	48	38	3	1

Методическиеуказаниядля выполнения работы
Решение задач в среде EXCEL начинается с ввода условий задачи. Ввод условий задачи состоит из следующих основных шагов:

• 
  создание формы для ввода условий задачи;
  
• 
  ввод исходных данных;
  
• 
  ввод зависимостей из математической модели;
  
• 
  назначение целевой функции;
  
• 
  ввод ограничений и граничных условий.
  

Последовательность работ рассмотрим на примере задачи составления производственного плана.

Пусть требуется определить, в каком количестве необходимо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4 для изготовления которой требуются ресурсы трех видов: трудовые ресурсы, сырье, финансы. Нормы расхода ресурсов каждого вида для выпуска единицы продукции, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в табл. 1. Количество расходуемых ресурсов не должно превышать имеющихся запасов.
Таблица 1

Ресурсы		Виды продукции			Запасы ресурсов
	Прод. 1	Прод. 2	Прод.3	Прод.4
Трудовые	3	1	2	4	440
Сырье	1	8	6	2	200
Финансы	1	4	7	2	320
Прибыль	7	3	6	12

Математическая модель для решения данной задачи:

^F=7x1^+3x2^+6x3^+12x4^{max; 3x}1^+x2^+2x3^+4x4 <sup>440;

x</sup>1^+8x2^+6x3^+2x4 ^{200; x}1^+4x2^+7x3^+2x4 <sup>320;


x</sup>j ^{0, j=1,4 .}

Форма для ввода условий данной задачи может иметь следующий вид: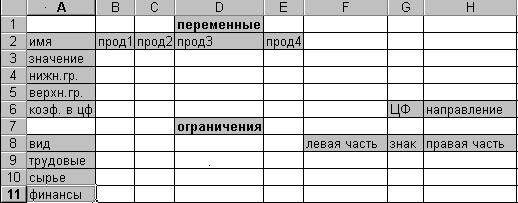


Рис. 1

Весь текст на рис.1 (и в дальнейшем) является комментарием и на решение задачи не влияет.

Далее необходимо ввести в сформированную форму исходные данные (коэффициенты в целевой функции и ограничениях, а также направление оптимизации целевой функции и знаки ограничений (рис.2)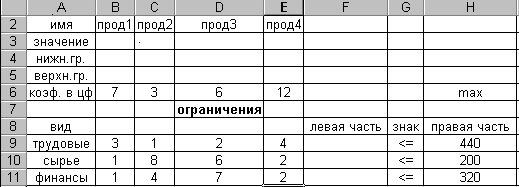


Рис.2

При этом ячейки B3:E3 являются изменяемыми и в них будут заноситься значения переменных.

Ввод функциональных зависимостей для целевой функции и ограничений осуществляется с использованием Мастера'>Мастера функций. Для этого необходимо активизировать требуемую ячейку (F6) и вызвать Мастер функций. В левой

части появившегося диалогового окна нужно выбрать категорию функции Математическая,а в правом окне выделить функцию СУММПРОИЗВ и нажать клавишу ОК. Затем на экране отобразится диалоговое окно второго шага (рис.8), где требуется ввести как первый (B$3:E$3), так и второй массивы (B6:E6). При вводе первого массива используются абсолютные ссылки на ячейки, при вводе второго - относительные, что в дальнейшем будет удобно при копировании формул. Во все окна адреса ячеек удобно вводить не с клавиатуры, а протаскивая мышь по соответствующим ячейкам.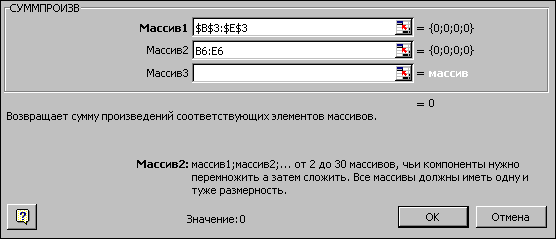


Рис.3
Зависимости для левых частей ограничений вводятся аналогично. При этом необходимо лишь менять адреса ячеек. Для ускорения и удобства ввода можно скопировать содержимое ячейки F6 в ячейки F9, F10 и F11 (при этом все относительные ссылки изменятся автоматически).

Окончательная таблица с исходными данными представлена на рис.4.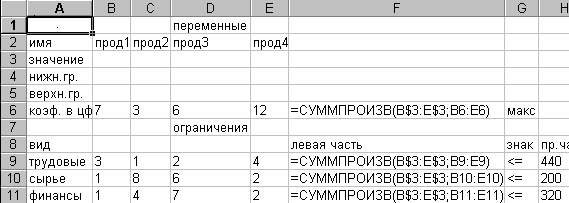


Рис. 4

После окончания ввода исходных данных осуществляется вызов программы Поиск решения.Для этого необходимо выбрать в меню пункт Данные, а в нем – Поиск решения, в результате чего на экране появится окно поиска решения (рис.5).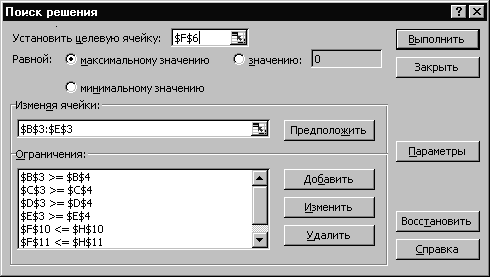


Рис.5

В окне Установить целевую ячейку требуется ввести имя ячейки, в которую введена зависимость для целевой функции (в данном случае F6). В качестве направления оптимизации выбирается максимизация. В окне Изменяя ячейки вводятся адреса ячеек, соответствующих варьируемым переменным задачи ($B3:$E3). Далее необходимо ввести ограничения. Для добавления ограничений выбирается пункт Добавить, после чего появляется окно добавления ограничений (рис.6)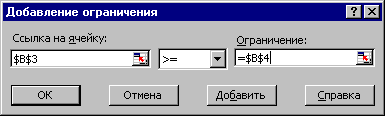



Рис.6
Вводятся граничные условия для переменных (Прод1 - Прод4) 0:

$B3>= $B4, $C3 >= $C4, $D3 >= $D4, $E3 >= $E4 (нулевые значения ячеек B4-E4

можно не устанавливать). Ограничения можно также ввести в виде $B3 >= 0, $C3

>= 0, $D3 >= 0, $E3 >= 0. Затем вводятся ограничения на ресурсы: $F9 <=

$H9, $F10 <= $H10, $F11 <= $H11. Ограничения вводят последовательно. Сначала выбирается пункт Добавить, далее в появившихся диалоговых окнах вводится левая часть, знак и правая часть каждого ограничения. После ввода последнего ограничения и нажатия OK произойдет возврат в окно Поиск решения.

Решение задачи производится сразу же после ввода данных, когда на экране находится диалоговое окно Поиск решения. Перед началом решения необходимо установить параметры решения, для чего в окне поиска решения выбрать команду параметры. Диалоговое окно параметров поиска решения представлено на рис. 7.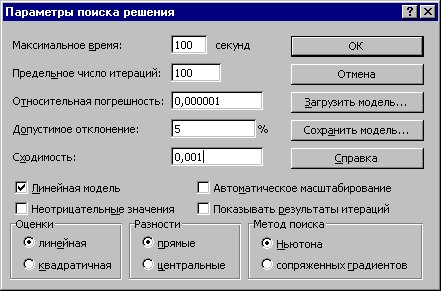



Рис.7
С помощью команд, находящихся в этом диалоговом окне, можно вводить условия для решения задач оптимизации всех классов. Рассмотрим наиболее важные команды, применяемые при решении конкретных задач.