Теория оптимизации

• Название: Теория оптимизации
• Дата: 10.05.2023
• Размер: 260.45 Kb.
• Имя файла: Laboratornyie-rabotyi-1-2-TOiPR.docx
• Тип: Решение; #1120224
• страница: 3 из 6

Линейная модель

Используется для решения линейной задачи оптимизации или линейной аппроксимации нелинейной задачи.

Показывать результаты итераций

Используется для приостановки поиска решения для просмотра результатов отдельных итераций.

Автоматическое масштабирование

Служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине, например, максимизация прибыли в процентах по отношению к вложениям в миллионах рублей.

Значения не отрицательны

Позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение.

Остальные команды будут рассмотрены позже при изучении соответствующих классов задач.

Для решения задачи линейного программирования необходимо установить флажок Линейная модель в окне Параметры поиска решения, что обеспечит использование симплексного метода. Далее после выбора OK произойдет возврат в окно Поиск решения. Запуск процесса решения задачи осуществляется командой Выполнить.

Решение задачи занимает несколько секунд, после чего на экране появляется диалоговое окно Результаты поиска решения. При решении рассматриваемой задачи производственного планирования в окне появится сообщение о том, что решение найдено. В данном окне предоставляется возможность или сохранить найденное решение во влияющих ячейках модели,

или восстановить исходные данные. Для этого необходимо отметить нужный пункт.

Результирующие значения всех переменных записываются в ячейки B3- E3 исходной задачи. Соответствующее значение целевой функции заносится в ячейку F6, а значения левых частей ограничений – в ячейки F9-F11. Таблица с результатами решения задачи представлена на рис. 8.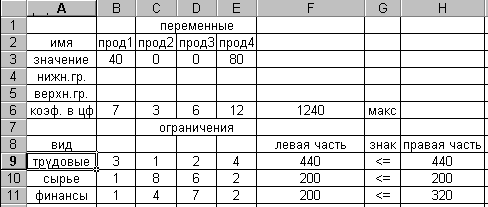

Рис.8

Рис. 8 показывает, что в оптимальном решении

Прод1 = В3 = 40; Прод2 = С3 = 0; Прод3 = D3 = 0; Прод4 = Е3 = 80.

При этом максимальная прибыль будет составлять F6 = 1240, а количество использованных ресурсов равно:

трудовых = F9 = 440,сырья = F10 = 200,финансов = F11 = 200.

Таково оптимальное решение рассматриваемой задачи производственного планирования. Однако решение задачи находится не всегда. Если условия задачи несовместны, на экране появится надпись - Поиск не может найти подходящего решения. Если целевая функция не ограничена, то в окне результатов поиска решения появится сообщение: Значения целевой функции не сходятся.

Кроме этого, из окна Результаты поиска решения возможно создание отчётов трех типов: по результатам, устойчивости и пределам, каждый из которых записывается на отдельном листе. Отчеты используются при анализе полученного оптимального решения.

Отчет по результатам (рис. 9) состоит из трех таблиц.

В таблице 1 (целевая ячейка) приведены сведения о целевой функции, в столбце "Исходно" - указывается значение целевой функции до вычислений, "Результат" - указывается значение целевой функции после вычислений.

Таблица 2 (изменяемые ячейки) содержит сведения о значениях искомых переменных, до и после решения задачи.

Таблица 3 (ограничения) показывает результаты оптимального решения для ограничений и для граничных условий. Здесь в графе "Формула" приведены зависимости, которые были введены в диалоговом окне "Поиск решения"); в графе "Разница" показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе "Состояние" указывается связанное; при неполном использовании ресурса в этой графе указывается несвязан.



Рис.9
Отчет по устойчивости (рис. 10) состоит из двух таблиц.

В таблице 1 (изменяемые ячейки) приводятся следующие значения для переменных:

• 
  результат решения задачи;
  
• 
  редуцированная стоимость, т.е. дополнительные двойственные переменные v_j, которые показывают, насколько изменяется целевая функция при принудительном включении единицы этой продукции в оптимальное решение;
  
• 
  коэффициенты целевой функции;
  

-предельные значения приращения коэффициентов c_j целевой функции при которых сохраняется набор переменных, входящих в оптимальное решение.

В таблице 2 (ограничения) приводятся аналогичные значения для ограничений:

• 
  величины использованных ресурсов;
  
• 
  теневые цены, т.е. двойственные оценки y_i, которые показывают, как изменится целевая функция при изменении ресурсов на единицу;
  
• 
  значения приращения ресурсов b_i, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.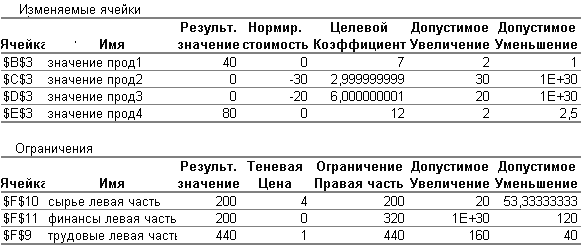
  

Рис. 10
Отчет по пределам (рис.11) показывает, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения:

• 
  рассматриваются значения x_j в оптимальном решении;
  
• 
  рассматриваются нижние пределы изменения значений x_j.
  

Кроме этого, в отчете указаны значения целевой функции при выпуске данного типа продукции на нижнем пределе. Далее приводятся верхние пределы изменения x_j и значения целевой функции при выпуске продукции, вошедшей в оптимальное решение на верхних пределах.


Рис. 11

Важным фактором, помогающим принять оптимальное решение, является наглядное представление полученного результата. Результат решения задачи, рассмотренной выше, примем в качестве исходных данных при рассмотрении вопросов построения диаграмм.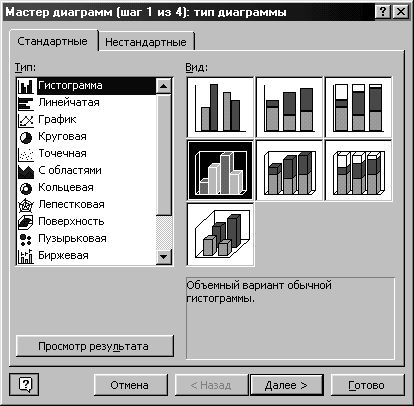


Рис. 12
Для построения диаграмм необходимо выделить те ячейки, значения которых должны быть представлены на диаграмме (B3:E3). Затем вызывается Мастер диаграмм (рис. 12). В появившемся диалоговом окне выбирается нужный тип диаграммы. Выберем, например, объемный вариант гистограммы.

После выбора типа диаграммы осуществляется переход к следующему этапу построения диаграммы. В диалоговом окне Исходные данные (рис.13) сначала необходимо ввести диапазон данных, которые отбражаются на диаграмме (в нашем примере ячейки B3:E3), а затем, выбрав команду Ряд, ввести названия рядов (например, “Количество продукции”), а также подписи под осью X (Прод1, Прод2, Прод3, Прод4). Для ввода подписей можно выделить соответствующие ячейки таблицы (B2:E2) или ввести подписи непосредственно в диалоговом окне через двоеточие.

После окончания работы с окном Исходные данные необходимо выбрать пункт Далее и перейти в диалоговое окно Параметры диаграммы (рис. 14). В данном окне, если необходимо, вводится заголовок диаграммы, размещается легенда, подписываются оси, определяются линии сетки. Все вводимые изменения отображаются на диаграмме. Затем осуществляется переход в

диалоговое окно Размещение диаграммы и выбирается тип размещения: на отдельном рабочем листе или на имеющемся рабочем листе. После выбора пункта Готово диаграмма размещается на указанном листе. Построенная гистограмма для рассматриваемой задачи представлена на рис. 15.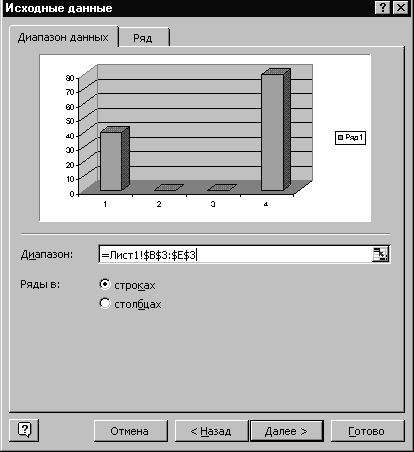


Рис. 13
Возможно перемещение данной диаграммы, изменение её размеров, перестройка параметров. Для этого необходимо активизировать нужную диаграмму с помощью мыши и в режиме форматирования диаграммы выполнить необходимые действия.

Рис.14



Рис. 15