Теория оптимизации

• Название: Теория оптимизации
• Дата: 10.05.2023
• Размер: 260.45 Kb.
• Имя файла: Laboratornyie-rabotyi-1-2-TOiPR.docx
• Тип: Решение; #1120224
• страница: 6 из 6

ЛАБОРАТОРНАЯ РАБОТА №2

РЕШЕНИЕ ТРАНСПОРТНЫХ ЗАДАЧ СРЕДСТВАМИ EXCEL
Цельработы: Получение практических навыков решения задач линейного программирования транспортного типа в среде EXCEL.
Лабораторныезадания.

1. 
   По лекциям и учебному пособию ознакомиться с постановкой и методом решения транспортных задач линейной оптимизации (ГЛАВА 3, п. 3.5.1).
   
2. 
   В соответствии с вариантом решить с использованием средств EXCEL все предлагаемыезадачи(пункты1,2,3). В задаче 3 открытую модель необходимо предварительно преобразовать к закрытой. Сформировать отчеты, построить диаграммы. Проанализировать полученные результаты.
   
3. 
   Решить транспортную задачу изпункта1вручную с использованием метода потенциалов (метод изложен в учебном пособии, п. 3.5.1). !!!Вручную решается только одна задача (из пункта 1). Задачи с дополнительными ограничениями и с открытой моделью вручную решать не надо.
   
4. 
   Сравнить результаты, полученные при выполнении лабораторных заданий 1 и 2, сделать выводы.
   

Отчет полабораторнойработедолженсодержать:

1. 
   Постановки решаемых транспортных задач.
   
2. 
   Математические оптимизационные модели решаемых транспортных задач.
   
3. 
   Результаты решения задач средствами EXCEL (покаждойзадаче отдельно).
   
4. 
   Сформированные отчеты, построенные диаграммы.
   
5. 
   Решение задачи из п.1 вручную с использованием метода потенциалов.
   
6. 
   Выводы.
   

Вариант1.

1. 
   Решить транспортную задачу
   

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
А1	2	4	7	9	200
A2	5	1	8	12	270
А3	11	6	4	3	140
Потребности	120	80	250	160

2. 
   Решить задачу из п. 1 при следующих дополнительных условиях: из пункта А1 в пункт В3 должно быть перевезено не более 20 единиц груза, из пункта А2 в пункт В2 перевозка груза запрещена, а из пункта А3 в пункт В1 необходимо перевезти не менее 5 единиц груза.
   
3. 
   Решить задачу из п. 1, если запас пункта отправления A1 составит 150 единиц, а потребность пункта назначения B4 200 единиц (открытая модель).
   

Вариант2.

1. 
   Решить транспортную задачу
   

   Пункты отправления	Пункты назначения				Запасы
   	B1	B2	B3	B4
   А1	3	2	7	9	190
   A2	8	3	5	10	250
   А3	10	6	2	4	280
   Потребности	220	100	250	150

2. 
   Решить задачу при следующих дополнительных условиях: из пункта А2 в пункт В4 должно быть перевезено не более 30 единиц груза, из пункта А1 в пункт В2 перевозка груза запрещена, а из пункта А3 в пункт В3 необходимо перевезти не менее 10 единиц груза.
   
3. 
   Решить задачу из п. 1, если запас пункта отправления A1 составит 150 единиц, а потребность пункта назначения B4 200 единиц (открытая модель).
   

Вариант3.

1. 
   Решить транспортную задачу
   

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
А1	8	6	8	3	250
A2	3	3	5	18	300
А3	13	5	7	2	130
Потребности	150	100	260	170

2. 
   Решить задачу при следующих дополнительных условиях: из пункта А3 в пункт В1 должно быть перевезено не более 30 единиц груза, из пункта А2 в пункт
   

В2 перевозка груза запрещена, а из пункта А1 в пункт В1 необходимо перевезти не менее 15 единиц груза.

3. 
   Решить задачу из п. 1, если запас пункта отправления A1 составит 200 единиц, а потребность пункта назначения B4 200 единиц (открытая модель).
   

Вариант4

1. 
   Решить транспортную задачу
   

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
А1	4	5	7	8	300
A2	5	6	3	11	470
А3	8	9	6	3	230
Потребности	220	180	340	260

2. 
   Решить задачу при следующих дополнительных условиях: Из пункта А2 в пункт В2 должно быть перевезено не более 50 единиц груза, из пункта А2 в пункт В3 перевозка груза запрещена, а из пункта А3 в пункт В4 необходимо перевезти не менее 25 единиц груза.
   
3. 
   Решить задачу из п. 1, если запас пункта отправления A3 составит 150 единиц, а потребность пункта назначения B2 300 единиц (открытая модель).
   

Вариант5.

1. 
   Решить транспортную задачу
   

   Пункты отправления	Пункты назначения				Запасы
   	B1	B2	B3	B4
   А1	11	6	4	3	100
   A2	5	1	8	12	270
   А3	2	4	7	9	280
   Потребности	140	180	200	130

2. 
   Решить задачу при следующих дополнительных условиях: Из пункта А1 в пункт В1 должно быть перевезено не более 30 единиц груза, из пункта А2 в пункт В4 перевозка груза запрещена, а из пункта А3 в пункт В3 необходимо перевезти не менее 35 единиц груза.
   
3. 
   Решить задачу из п. 1, если запас пункта отправления A2 составит 150 единиц, а потребность пункта назначения B1 200 единиц (открытая модель).
   

Вариант6.

1. 
   Решить транспортную задачу
   

   Пункты отправления	Пункты назначения				Запасы
   	B1	B2	B3	B4
   А1	4	5	8	6	200
   A2	7	1	2	2	150
   А3	9	3	9	6	300
   Потребности	150	170	100	230

2. 
   Решить задачу при следующих дополнительных условиях: Из пункта А2 в пункт В3 должно быть перевезено не более 60 единиц груза, из пункта А1 в пункт В3 перевозка груза запрещена, а из пункта А2 в пункт В3 необходимо перевезти не менее 25 единиц груза.
   
3. 
   Решить задачу из п. 1, если запас пункта отправления A3 составит 250 единиц, а потребность пункта назначения B2 200 единиц (открытая модель).
   

Вариант7.

1. 
   Решить транспортную задачу
   

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
А1	9	4	4	3	120
A2	6	2	3	11	250
А3	3	5	8	2	280
Потребности	240	80	150	180

2. 
   Решить задачу при следующих дополнительных условиях: Из пункта А3 в пункт В1 должно быть перевезено не более 20 единиц груза, из пункта А1 в пункт В4 перевозка груза запрещена, а из пункта А2 в пункт В3 необходимо перевезти не менее 45 единиц груза.
   
3. 
   Решить задачу из п. 1, если запас пункта отправления A2 составит 150 единиц, а потребность пункта назначения B4 200 единиц (открытая модель).
   

Вариант8.

1. 
   Решить транспортную задачу
   

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
А1	12	5	3	2	110
A2	7	2	9	11	280
А3	3	5	6	7	260
Потребности	120	200	230	100

2. 
   Решить задачу при следующих дополнительных условиях: Из пункта А2 в пункт В3 должно быть перевезено не более 50 единиц груза, из пункта А1 в пункт В4 перевозка груза запрещена, а из пункта А3 в пункт В3 необходимо перевезти не менее 30 единиц груза.
   
3. 
   Решить задачу из п. 1, если запас пункта отправления A3 составит 150 единиц, а потребность пункта назначения B1 200 единиц (открытая модель).
   

Вариант9.

1. 
   Решить транспортную задачу
   

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
А1	15	7	5	4	130
A2	4	2	9	10	250
А3	3	3	6	5	270
Потребности	160	140	200	150

2. 
   Решить задачу при следующих дополнительных условиях: Из пункта А3 в пункт В3 должно быть перевезено не более 40 единиц груза, из пункта А1 в пункт В4 перевозка груза запрещена, а из пункта А3 в пункт В1 необходимо перевезти не менее 15 единиц груза.
   
3. 
   Решить задачу из п. 1, если запас пункта отправления A2 составит 150 единиц, а потребность пункта назначения B4 200 единиц (открытая модель).
   

Вариант10.

1. 
   Решить транспортную задачу
   

Пункты отправления	Пункты назначения				Запасы
	B1	B2	B3	B4
А1	12	7	6	4	200
A2	6	2	8	11	170
А3	3	5	2	8	280
Потребности	120	200	100	230

2. 
   Решить задачу при следующих дополнительных условиях: Из пункта А1 в пункт В2 должно быть перевезено не более 20 единиц груза, из пункта А2 в пункт В4 перевозка груза запрещена, а из пункта А3 в пункт В3 необходимо перевезти не менее 15 единиц груза.
   
3. 
   Решить задачу из п. 1, если запас пункта отправления A3 составит 150 единиц, а потребность пункта назначения B2 200 единиц (открытая модель).
   

Методическиеуказаниядля выполнения работы

Рассмотрим пример решения средствами EXCEL следующей транспортной задачи:

Производственное объединение имеет в своем составе четыре филиала, которые производят однородную продукцию соответственно в количествах 12, 28

,11 и 14 единиц. Эту продукцию получают три потребителя, расположенные в разных местах. Их потребности в продукции равны соответственно 20, 30, и 15 единиц. Тарифы перевозок единицы продукции от каждого из филиалов соответствующим потребителям задаются матрицей

_1



_{C }12

^10

_

_5

7 8 _



4 6 _

15 14 ^



13 16 ^

Математическая модель для определения плана перевозок минимальной стоимости в данном случае имеет следующий вид:

x₁₁+7x₁₂+8x₁₃+12x₂₁+4x₂₂+6x₂₃+10x₃₁+15x₃₂+14x₃₃+5x₄₁+13x₄₂+16x₄₃ min; x₁₁+x₁₂+x₁₃₌12;

x₂₁+x₂₂+x₂₃=28;

x₃₁+x₃₂+x₃₃=11; x₄₁+x₄₂+x₄₃=14; x₁₁+x₂₁+x₃₁+x₄₁₌20; x₁₂+x₂₂+x₃₂+x₄₂=30; X₁₃+x₂₃+x₃₃+x₄₃=15;

x_ij0,

i 1,4, j 1,3.

Таблица EXCEL с введенными условиями данной задачи представлена на рис. 25. Ввод исходных данных для транспортной задачи аналогичен вводу условий обычной задачи линейного программирования. Сначала составляется форма для ввода, затем в полученную форму вводятся исходные данные задачи (запасы, потребности, тарифы на перевозку), далее осуществляется ввод зависимости для целевой функции и зависимостей для левых частей всех ограничений.



Рис.25

В ячейки F3-F6 занесены запасы всех пунктов отправления, в ячейки B8-D8

- потребности пунктов назначения. Значения тарифов на перевозку записаны в ячейках B11-D14. Ячейки B3-D6 соответствуют переменным задачи и в них после решения будут занесены значения перевозимых грузов. Ячейки E3-E6, B7-D7 соответствуют левым частям ограничений. Зависимость для целевой функции заносится в ячейку F8.

Для решения задачи вызывается программа Поиск решения. В появившемся диалоговом окне назначается целевая функция (ячейка F8), определяется направление поиска (минимизация), вводятся адреса искомых переменных (ячейки В3-D6). Для ввода ограничений выбирается команда Добавить. В появившемся диалоговом окне Добавление ограничений вводятся ограничения $B$7=$B$8, $C$7=$C$8, $D$7=$D$8, $E$3=$F$3, $E$4=$F$4,

$E$5=$F$5, $E$6=$F$6 .

Далее выбирается пункт Параметры и в появившемся диалоговом окне Параметры поиска решения устанавливается флажок Линейная модель и Неотрицательные значения. Результаты решения задачи представлены на рис. 26.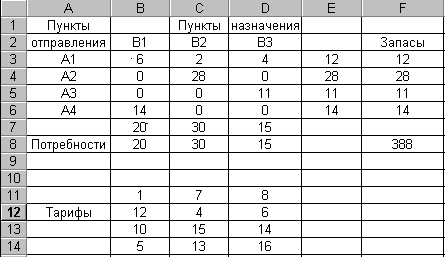

Рис. 26

Анализ оптимального решения транспортной задачи производится так же, как и для обычных задач линейного программирования. Могут быть созданы отчеты по результатам, пределам и устойчивости.

Если в условиях задачи существует запрет на перевозку (например, из

пункта A_i в пункт

B _j перевозка грузов запрещена), то тариф

^cij

приравнивается

какому-либо большому числу, либо при задании оптимизационной модели вводится ограничение x_ij=0.