Теория программирования. Теория программирования
 Скачать 195.28 Kb. Скачать 195.28 Kb.
|
|
Тема 4. Типы переменных. Целые и вещественные переменные, представление целых и вещественных чисел в компьютере Содержание темы: типы переменных, целочисленные и вещественные переменные, символьные переменные, логические переменные и выражения, массивы, текстовые строки Цели и задачи изучения темы: получить знания об основных типах переменных, о представлении целых и вещественных чисел в компьютере Изучая тему, необходимо акцентировать внимание на следующих понятиях: · тип переменной – определяется множеством значений, которое она может принимать; · целочисленная переменная – может хранить числа от нуля до 2 в 32-й степени минус 1; · вещественная переменная – представляется в компьютере в так называемой экспоненциальной, или плавающей, форме; · символьная переменная – представляется целочисленным кодом в некоторой фиксированной кодировке; · логические или условные выражения – используются в качестве условия в конструкциях ветвления; · массив переменных – объединение определенного числа однотипных данных, называемых элементамимассива; · текстовая строка – представляется массивами символов 4.1. Типы переменных Тип переменной определяется множеством значений, которое она может принимать. Кроме того, тип определяет операции, которые возможны с переменной. Например, с численными переменными возможны арифметические операции, с логическими - проверка, истинно или ложно значение переменной, с символьными - сравнение, с табличными (или массивами) – чтение или запись элемента таблицы с заданным индексом и т.п. Как правило, в любом современном языке имеется базовый набор типов и несколько конструкций, которые позволяют строить новые типы из уже созданных. Наборы базовых типов и конструкций различаются для разных языков. В описании неформального алгоритмического языка будут использоваться типы и конструкции, которые присутствуют в большинстве языков практического программирования. 4.2. Целочисленные переменные Тип целое число является основным для любого алгоритмического языка. Связано это с тем, что содержимое ячейки памяти или регистра процессора можно рассматривать как целое число. Адреса элементов памяти также представляют собой целые числа, с их помощью записываются машинные команды и т.д. Символы представляются в компьютере целыми числами - их кодами в некоторой кодировке. Изображения также задаются массивами целых чисел: для каждой точки цветного изображения хранятся интенсивности ее красной, зеленой и синей составляющей (в большинстве случаев - в диапазоне от 0 до 255). Как говорят математики, целые числа даны свыше, все остальное сконструировал из них человек. Общепринятый в программировании термин целое число или целочисленная переменная, строго говоря, не вполне корректен. Целых чисел бесконечно много, десятичная или двоичная запись целого числа может быть сколь угодно длинной и не помещаться в области памяти, отведенной под одну переменную. Целая переменная в компьютере может хранить лишь ограниченное множество целых чисел в некотором интервале. В современных компьютерах под целую переменную отводится 4 байта, т.е. 32 двоичных разряда. Она может хранить числа от нуля до 2 в 32-й степени минус 1. Таким образом, максимальное целое число, которое может храниться в целочисленной переменной, равно 232 - 1 = 4294967295 Сложение и умножение значений целых переменных выполняется следующим образом: сначала производится арифметическая операция, затем старшие разряды результата, вышедшие за границу тридцати двух двоичных разрядов (т.е. четырех байтов), отбрасываются. Определенные таким образом операции удовлетворяют традиционным законам коммутативности, ассоциативности и дистрибутивности: a+b = b+a, ab = ba (a+b) + c = a+(b+c), (ab)c = a(bc) a(b+c) = ab+ac В языке Си целым числам соответствуют типы int, char и bool. Представление целочисленных значений в памяти компьютера в большинстве случаев реализуется аппаратным способом с учетом возможностей конкретного процессора. Также аппаратно реализуется примитивный набор операций над этими значениями. Применение операций, реализуемых аппаратно, значительно более эффективно, чем использование программно реализуемых операций. Поэтому компиляторы по возможности формируют код, в котором применяется аппаратная реализация примитивных операций (таких, как сложение, вычитание, умножение и деление). Целочисленное значение типа integer (целое) может иметь в памяти компьютера следующее представление: 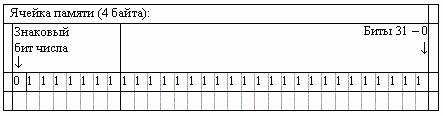 Рис. 4.1. Битовая структура типа integer 4.3. Вещественные переменные Вещественные числа представляются в компьютере в так называемой экспоненциальной, или плавающей, форме. Вещественное число r имеет вид r = ±2e* m Представление числа состоит из трех элементов: 1. знак числа - плюс или минус. Под знак числа отводится один бит в двоичном представлении, он располагается в старшем, т.е. знаковом разряде. Единица соответствует знаку минус, т.е. отрицательному числу, ноль - знаку плюс. У нуля знаковый разряд также нулевой; 2. показатель степени e, его называют порядком или экспонентой. Экспонента указывает степень двойки, на которую домножается число. Экспонента может быть как положительной, так и отрицательной (для чисел, меньших единицы). Под экспоненту отводится фиксированное число двоичных разрядов, обычно восемь или одиннадцать, расположенных в старшей части двоичного представления числа, сразу вслед за знаковым разрядом; 3. мантисса m представляет собой фиксированное количество разрядов двоичной записи вещественного числа в диапазоне от 1 до 2: 1 ≤ m <2 Следует подчеркнуть, что левое неравенство нестрогое - мантисса может равняться единице, а правое - строгое, мантисса всегда меньше двух. Разряды мантиссы включают один разряд целой части, который ввиду приведенного неравенства всегда равен единице, и фиксированное количество разрядов дробной части. Поскольку старший двоичный разряд мантиссы всегда равен единице, хранить его необязательно, и в двоичном коде он отсутствует. Фактически двоичный код хранит только разряды дробной части мантиссы. В языке Си вещественным числам соответствуют типы float и double. Элемент типа float занимает 4 байта, в которых один бит отводится под знак, восемь - под порядок, остальные 23 - под мантиссу (на самом деле, в мантиссе 24 разряда, но старший разряд всегда равен единице, поэтому хранить его не нужно). Тип double занимает 8 байтов, в них один разряд отводится под знак, 11 - под порядок, остальные 52 - под мантиссу. На самом деле в мантиссе 53 разряда, но старший всегда равен единице и поэтому не хранится. Поскольку порядок может быть положительным и отрицательным, в двоичном коде он хранится в смещенном виде: к нему прибавляется константа, равная абсолютной величине максимального по модулю отрицательного порядка. В случае типа float она равна 127, в случае double - 1023. Таким образом, максимальный по модулю отрицательный порядок представляется нулевым кодом. Основным типом является тип double, именно он наиболее естественен для компьютера. В программировании следует по возможности избегать типа float, так как его точность недостаточна, а процессор все равно при выполнении операций преобразует его в тип double. (Один из немногих случаев, где применение типа float оправдано, - трехмерная компьютерная графика.) Действия с плавающими числами из-за ошибок округления лишь приближенно отражают арифметику настоящих вещественных чисел. Так, если к большому плавающему числу прибавить очень маленькое, то оно не изменится. Действительно, при выравнивании порядков все значащие биты мантиссы меньшего числа могут выйти за пределы разрядной сетки, в результате чего оно станет равным нулю. Таким образом, с плавающими числами возможна ситуация, когда a+b = a при b ≠ 0 Более того, для сложения не выполняется закон ассоциативности: a+(b+c) ≠ (a+b)+c Приблизительно точность вычислений вещественных чисел типа double составляет 16 десятичных цифр. В случае четырехбайтовых плавающих чисел (тип float языка Си) точность вычислений составляет примерно 7 десятичных цифр. Это очень мало, поэтому тип float чрезвычайно редко применяется на практике. К тому же процессор сконструирован для работы с восьмибайтовыми вещественными числами, а при работе с четырехбайтовыми он все равно сначала приводит их к восьмибайтовому типу. В программировании следует избегать типа float и всегда пользоваться типом double. Кроме потери точности, при операциях с вещественными числами могут происходить и другие неприятности: 1. переполнение - когда порядок результата больше максимально возможного значения. Эта ошибка часто возникает при умножении больших чисел; 2. исчезновение порядка - когда порядок результата отрицательный и слишком большой по абсолютной величине, т.е. порядок меньше минимально допустимого значения. Эта ошибка может возникнуть при делении маленького числа на очень большое или при умножении двух очень маленьких по абсолютной величине чисел. Кроме того, некорректной операцией является деление на ноль. В отличие от операций с целыми числами, переполнение и исчезновение порядка считаются ошибочными ситуациями и приводят к аппаратному прерыванию работы процессора. Программист может задать реакцию на прерывание - либо аварийное завершение программы, либо, например, при переполнении присваивать результату специальное значение плюс или минус бесконечность, а при исчезновении порядка - ноль. Запись вещественных констант Вещественные константы записываются в двух формах - с фиксированной десятичной точкой или в экспоненциальном виде. В первом случае точка используется для разделения целой и дробной частей константы. Как целая, так и дробная части могут отсутствовать. Примеры: 1.2, 0.725, 1., .35, 0. В трех последних случаях отсутствует либо дробная, либо целая часть. Десятичная точка должна обязательно присутствовать, иначе константа считается целой. Отметим, что в программировании именно точка, а не запятая, используется для отделении дробной части; запятая обычно служит для разделения элементов списка. Экспоненциальная форма записи вещественной константы содержит знак, мантиссу и десятичный порядок (экспоненту). Мантисса - это любая положительная вещественная константа в форме с фиксированной точкой или целая константа. Порядок указывает степень числа 10, на которую домножается мантисса. Порядок отделяется от мантиссы буквой "e" (от слова exponent), она может быть прописной или строчной. Порядок может иметь знак плюс или минус, в случае положительного порядка знак плюс можно опускать. Примеры: 1.5e+6 константа эквивалентна 1500000.0 1e-4 константа эквивалентна 0.0001 -.75E3 константа эквивалентна -750.0 Вещественные типы аппаратно могут иметь два представления: вещественные числа с фиксированной точкой и вещественные числа с плавающей точкой. Как правило, по умолчанию компиляторы преобразуют вещественные значения в экспоненциальный формат (формат с плавающей точкой), если синтаксис языка явно не указывает применение формата с фиксированной точкой. Вещественное значение с плавающей точкой может иметь в памяти компьютера следующее представление:  Рис.4.2. Битовая структура типа float Для представления вещественных чисел с плавающей точкой и вещественных чисел двойной точности с плавающей точкой стандартом IEEE 754 определены 32- и 64-битовые представления соответственно. В разряды мантиссы записываются значащие цифры, а в разряды экспоненты заносится показатель степени. Положительные значения содержат в знаковом бите числа - 0, а отрицательные значения - 1. При обозначении чисел с плавающей точкой приняты следующие соглашения: знаковый разряд обозначается буквой s, экспонента - e, а мантисса - m. 4.4. Символьные переменные Значением символьной переменной является один символ из фиксированного набора. Такой набор обычно включает буквы, цифры, знаки препинания, знаки математических операций и различные специальные символы (процент, амперсенд, звездочка, косая черта и др.). Конечно, в памяти компьютера никаких символов не содержится. Символы представляются их целочисленными кодами в некоторой фиксированной кодировке. Кодировка определяется тремя параметрами: 1. диапазоном значений кодов. Например, самая распространенная в мире кодировка ASCII (от слов American Standard Code of Information Interchange - Американский стандартный код обмена информацией) имеет диапазон значений кодов от 0 до 127, т.е. требует семь бит на символ. Большинство современных кодировок имеют диапазон кодов от 0 до 255, т.е. один байт на символ. Наконец, сейчас во всем мире осуществляется переход на кодировку Unicode, которая использует коды в диапазоне от 0 до 65535, т.е. 2 байта на символ; 2. множеством изображаемых символов. Например, кодировка ASCII содержит буквы латинского алфавита, в западноевропейской кодировке к символам ASCII добавлены дополнительные знаки препинания, в частности, испанские перевернутые вопросительные и восклицательные знаки, и другие символы европейских языков, основанных на латинской графике. Любая из русских кодировок содержит кириллицу; 3. отображением множества кодов на множество символов. Например, русские кодировки КОИ-8 (Код обмена информацией восьмибитовый) и "Windows CP-1251", традиционно используемые в операционных системах Unix и MS Windows, имеют один и тот же диапазон кодов и один и тот же набор символов, но отображения их различны (одни и те же символы имеют разные коды в кодировках КОИ-8 и Windows). К сожалению, российские программисты не сумели договориться о единой кодировке русских букв. В настоящее время в России широко используются четыре различные кодировки: 1. кодировка КОИ-8 (это наиболее старый стандарт, принятый еще в конце 70-х годов XX века). КОИ-8 в основном используется в системе Unix и до недавнего времени была стандартом де-факто для русскоязычной электронной почты. Последнее время, однако, все чаще в электронной почте используют кодировку Windows; 2. так называемая альтернативная кодировка CP-866, которая используется в системе MS DOS. Она не удовлетворяет некоторым требованиям международных стандартов - например, ряд русских букв совпадает с кодами символов, используемых для управления передачей по линии. Альтернативная кодировка постепенно уходит в прошлое вместе с системой DOS; 3. кодировка Windows CP-1251, которая появилась значительно позже кодировки КОИ-8, но создатели русской версии Windows не захотели воспользоваться КОИ-8 (по-видимому, из-за того, что коды русских букв в КОИ-8 не упорядочены в соответствии с алфавитом; в CP-1251 коды русских букв упорядочены, за исключением буквы е). В связи с распространением операционной системы Windows, кодировка Windows получает все большее распространение; 4. кодировка, используемая в компьютерах Apple Macintosh. Существование различных кодировок русских букв сильно осложняет жизнь как программистам, так и обыкновенным пользователям: файлы при переносе из одной системы в другую приходится перекодировать, периодически возникают трудности при чтении писем, просмотре гипертекстовых страниц и т.п. Отметим, что ничего подобного нет ни в одной европейской стране. С повсеместным переходом на кодировку Unicode все проблемы такого рода должны исчезнуть. Кодировка Unicode включает символы алфавитов всех европейских стран и кириллицу. К сожалению, большинство существующих компьютерных программ приспособлено к представлению одного символа в виде одного байта. Поэтому в настоящее время часто используется промежуточное решение: компьютерные программы работают с внутренним представлением символов в кодировке Unicode (такое решение принято в языках Java и C#). При записи в файл символы Unicode приводятся к однобайтовой кодировке в соответствии с текущей языковой установкой. В языке Си символам соответствует тип char представляющий значение символа, реализуемое одним байтом. Для использования символов в кодировке Unicode язык C++ предоставляет тип wchar_t, в котором под каждый символ отводятся два байта. 4.5. Логические переменные и выражения В языке С++ определен логический тип данных bool, реализуемый одним байтом. Логические переменные принимают два значения: истина и ложь. Логические, или условные, выражения используются в качестве условия в конструкциях ветвления "если ... то ... иначе ... конец если" и цикла "пока". В первом случае в зависимости от истинности условия выполняется либо ветвь программы после ключевого слова "то", либо после "иначе"; во втором случае цикл выполняется до тех пор, пока условие продолжает оставаться истинным. В качестве элементарных условных выражений используются операции сравнения: можно проверить равенство двух выражений или определить, какое из них больше. Любая операция сравнения имеет два аргумента и вырабатывает логическое значение "истина" или "ложь" (true и false в языке C++). Мы будем обозначать операции сравнения так, как это принято в языке Си: · операция проверки равенства двух выражений обозначается двойным знаком равенства = = (мы не используем обычный знак равенства, поскольку знак равенства применяется для обозначения операции присваивания); · неравенство обозначается != (в Си восклицательный знак используется для отрицания); · для сравнения величин выражений применяются четыре операции больше >, больше или равно >=, меньше <, меньше или равно <=. Несколько примеров логических выражений: x == 0 - выражение истинно, если значение переменной x равно нулю, и ложно в противном случае; 0!= 0 - выражение ложно; 3>= 2 - выражение истинно. Из элементарных логических выражений и логических переменных можно составлять более сложные выражения, используя три логические операции "и", "или", "не": 1. результат логической операции "и" истинен, когда истинны оба ее аргумента. Например, логическое выражение 0 <= x и x <= 1 истинно, когда значение переменной x принадлежит отрезку [0, 1]. Логическую операцию "и" называют также логическим умножением или конъюнкцией; в языке Си логическое умножение обозначается двойным амперсандом &&; 2. результат логической операции "или" истинен, когда истинен хотя бы один из ее аргументов. Например, логическое выражение x != 0 или y != 0 ложно в том и только том случае, когда значения обеих переменных x и y равны нулю. Логическую операцию "или" называют также логическим сложением или дизъюнкцией; в Си логическое сложение обозначается двойной вертикальной чертой ||; 3. в отличие от логических операций "и" и "или", логическая операция "не" имеет только один аргумент. Ее результат истинен, когда аргумент ложен, и, наоборот, ложен, когда аргумент истинен. Например, логическое выражение не x == 0 истинно, когда значение переменной x отлично от нуля. Логическая операция "не" называется логическим отрицанием (иногда негацией); в Си логическое отрицание обозначается восклицательным знаком "!". В сложных логических выражениях можно использовать круглые скобки для указания порядка операций. При отсутствии скобок считается, что наивысший приоритет имеет логическое отрицание; затем идет логическое умножение, а низший приоритет у логического сложения. Обратим внимание на чрезвычайно важную особенность операций реализации логического сложения и умножения - так называемое сокращенное вычисление результата. А именно, в случае логического умножения всегда сначала вычисляется значение первого аргумента. Если оно ложно, то значение выражения полагается ложным, а второй аргумент не вычисляется вообще! Благодаря этой особенности можно корректно использовать выражения вроде x != 0 и y/x > 1 При вычислении значения этого выражения сначала вычисляется первый аргумент конъюнкции "x != 0". Если значение переменной x равно нулю, то первый аргумент ложен и значение второго аргумента "y/x > 1" уже не вычисляется. Это очень хорошо, поскольку при попытке его вычислить произошло бы аппаратное прерывание из-за деления на ноль. То же самое относится и к логическому сложению. Сначала всегда вычисляется первый аргумент логической операции "или". Если он истинен, то значение выражения полагается истинным, а второй аргумент не вычисляется вообще. Таким образом, операции логического сложения и умножения, строго говоря, не коммутативны. Может так случиться, что выражение "a и b" корректно, а выражение "b и a" - нет. Программисты очень часто сознательно используют эту особенность реализации логических операций. |
