Теория программирования. Теория программирования
 Скачать 195.28 Kb. Скачать 195.28 Kb.
|
|
Тема 3. Общее понятие алгоритма. Управляющие конструкции алгоритмического языка. Содержание темы: общее понятие алгоритма, управляющие конструкции алгоритмического языка, язык схем, основные структуры алгоритмов, понятие переменной Цели и задачи изучения темы: получить знания о написании алгоритма решения поставленной задачи, управляющих конструкциях алгоритмического языка, о важнейшем понятии алгоритмического языка – переменной Изучая тему, необходимо акцентировать внимание на следующих понятиях: · алгоритм– описание последовательности действий, которые необходимо выполнить для решения задачи; · псевдокод – алгоритмический язык, максимально приближенный к естественному; · ветвления и циклы – изменяют последовательное выполнение команд; · цикл с предусловием – условие продолжения цикла проверяется перед выполнением тела цикла; · переменная – именованная область в памяти компьютера, в которую могут записываться различные числовые или символьные значения; · присваивание – операция записи значения впеременную; · основные структуры алгоритмов– ограниченный набор стандартных способов соединения отдельных блоков или структур для выполнения типичных последовательностей действий; 3.1. Общее понятие алгоритма Понятие алгоритма – одно из основных понятий программирования и математики. Алгоритм – это последовательность команд, предназначенная исполнителю, в результате выполнения которой он должен решить поставленную задачу. Алгоритм записывается на формальном языке, исключающем неоднозначность толкования. В нашем случае исполнитель – это компьютер, но может быть и человек, автоматическое устройство и т.п. Запись алгоритма на формальном языке называется программой. Иногда само понятие алгоритма отождествляется с его записью, так что слова "алгоритм" и "программа" - почти синонимы. Небольшое различие заключается в том, что при упоминании алгоритма, как правило, имеют в виду основную идею его построения, общую для всех алгоритмических языков. Программа же всегда связана с записью алгоритма на конкретном формальном языке. В математике рассматриваются различные виды алгоритмов – программы для машин Тьюринга, алгоритмы Маркова (нормальные алгоритмы), частично рекурсивные функции и т.п. Знаменитый тезис Чёрча утверждает, что все виды алгоритмов эквивалентны друг другу, т.е. классы задач, решаемых разными типами алгоритмов, всегда совпадают. Тезис этот недоказуем (можно лишь доказать совпадение для двух конкретных типов алгоритмов, например, машин Тьюринга и нормальных алгоритмов), но никто в его верности не сомневается. Так что все языки программирования эквивалентны друг другу и различаются лишь тем, насколько они удобны для решения конкретных классов задач. Например, объектно-ориентированные языки оптимальны для программирования в оконных средах, а язык Фортран успешно применяется в научных и инженерных расчетах. Большинство используемых в программировании алгоритмических языков имеют общие черты. В то же время, при изложении идеи алгоритма, например, при публикации в научной статье, не всегда целесообразно пользоваться каким-либо конкретным языком программирования, чтобы не загромождать изложение несущественными деталями. В таких случаях применяется неформальный алгоритмический язык, максимально приближенный к естественному. Язык такого типа называют псевдокодом. Для специалиста не составляет труда переписать программу с псевдокода на любой конкретный язык программирования. Запись алгоритма на псевдокоде зачастую яснее и нагляднее, она дает возможность свободно выбирать уровень детализации, начиная от описания в самых общих чертах и кончая подробным изложением. Псевдокод объединяет существенные черты множества алгоритмических языков. Для записи алгоритмов в данном курсе будет использоваться как псевдокод, так и конкретные языки: Си, C++. 3.2. Управляющие конструкции алгоритмического языка Большинство алгоритмических языков относится к так называемым процедурным языкам, в которых основной единицей является оператор. Оператор представляет собой команду на выполнение некоторого действия. Язык, таким образом, состоит в основном из фраз в повелительном наклонении. Альтернативой операторам являются описания, определяющие объекты или типы объектов и их взаимосвязи. Считается, что чем больший процент составляют описания, тем более совершенным является язык. Существуют алгоритмические языки, состоящие в основном из описаний (функциональные языки), однако, данный курс ограничивается процедурными языками. Всякий алгоритм предназначен исполнителю, который однозначно понимает команды алгоритма. Пример: опишем алгоритм проезда от Аэровокзала в Москве до аэропорта Домодедово. алгоритм Проезд от Аэровокзала до Домодедово через МКАД | Дано: находимся у Аэровокзала | Надо: оказаться в аэропорту Домодедово начало алгоритма | повернуть направо на центральный проезд | Ленинградского проспекта в сторону центра; | проехать до второго светофора; | выполнить разворот на перекрестке | проехать по Ленинградскому проспекту из центра | до пересечения с Московской кольцевой дорогой; | переехать мост над кольцевой дорогой и | повернуть направо на внешнюю часть кольцевой дороги; | двигаться по кольцевой дороге в направлении против | часовой стрелки до Каширского шоссе; | повернуть направо на Каширское шоссе в сторону из города; | двигаться, никуда не сворачивая, до | аэропорта Домодедово; конец алгоритма Строки алгоритма представляют собой фразы в повелительном наклонении, которые предназначены исполнителю алгоритма, т.е. любому водителю, который может отличить внешнюю сторону кольцевой дороги от внутренней. Строки алгоритма выполняются последовательно; считается, что исполнитель алгоритма способен не задумываясь выполнить каждую его команду. Большинство алгоритмов не сводится, однако, к последовательному выполнению команд, в них присутствуют ветвления и циклы. При ветвлении в зависимости от условия выполняется одна из двух ветвей программы; для этого используется оператор "если ... то ... иначе ... конец если". Например, можно модифицировать приведенный выше алгоритм, используя выбор одного из двух альтернативных путей, в зависимости от наличия транспортной пробки. алгоритм Оптимальный путь от Аэровокзала до Домодедово | Дано: находимся у Аэровокзала | Надо: оказаться в аэропорту Домодедово начало алгоритма | если нет пробки на Ленинградском проспекте | | в направлении из центра | | то | | // ...выполняем предыдущий алгоритм... | | Проезд от Аэровокзала до Домодедово через МКАД | | иначе | | повернуть направо на боковой проезд | | Ленинградского проспекта в сторону центра; | | доехать до пересечения с Беговой улицей; | | повернуть направо на Третье транспортное кольцо; | | ехать по Третьему транспортному кольцу против | | часовой стрелки до пересечения с Варшавским шоссе; | | повернуть направо на Варшавское шоссе | | в сторону из центра; | | ехать прямо до развилки с Каширским шоссе; | | на развилке с Каширским шоссе проехать прямо в сторону | | Каширского шоссе; // Варшавское уходит направо | | двигаться, никуда не сворачивая, до | | аэропорта Домодедово; | конец если конец алгоритма Здесь исполнитель алгоритма сначала должен проверить условие Нет ли пробки на Ленинградском проспекте в направлении из центра Если это условие истинно, то выполняется первый алгоритм "Проезд от Аэровокзала до Домодедово через МКАД"; если ложно - часть алгоритма между строками "иначе" и "конец если". Второй важнейшей конструкцией алгоритмического языка является конструкция "цикл пока". Заголовок цикла состоит из ключевых слов "цикл пока", за которыми следует некоторое условие. Дальше записывается тело цикла, завершаемое строкой "конец цикла". При выполнении цикла исполнитель сначала проверяет условие в заголовке тела цикла. Если условие истинно, то выполняется тело цикла. Затем вновь проверяется условие в заголовке цикла, опять выполняется тело цикла, если условие истинно, и так до бесконечности. Если же условие ложно с самого начала или становится ложным в результате предыдущего выполнения тела цикла, то тело цикла не выполняется и цикл завершается. Таким образом, по выходу из цикла условие, записанное в его заголовке, всегда ложно. Если условие ложно перед началом цикла, то цикл не выполняется ни разу! Программисты иногда называют "цикл пока" циклом с предусловием, поскольку условие продолжения цикла проверяется перед выполнением тела цикла, а не после него. Иногда используют циклы с постусловием (do... while), когда тело цикла всегда выполняется хотя бы один раз, а условие продолжения проверяется после каждой итерации. Всегда предпочтительнее использовать цикл с предусловием, это помогает избежать многих ошибок. Для иллюстрации конструкции "цикл пока" можно привести следующую модификацию алгоритма проезда. алгоритм Добраться из Аэровокзала до Домодедово | Дано: находимся у Аэровокзала | Надо: оказаться в аэропорту Домодедово начало алгоритма | | цикл пока пробка на Ленинградском проспекте | | выпить чашку кофе в кафе Аэровокзала | | ждать полчаса | конец цикла | | Проезд от аэровокзала до Домодедово через МКАД конец алгоритма Здесь снова использован определенный ранее алгоритм "Проезд от аэровокзала до Домодедово". Условие продолжения цикла проверяется перед выполнением тела цикла, но не в процессе его выполнения! Так, если пробка рассосалась после чашки кофе, то все равно нужно ждать полчаса. Теперь можно подвести итоги. Запись алгоритма на неформальном языке представляет собой последовательность команд исполнителю алгоритма. Запись может также включать управляющие конструкции: ветвление, или условный оператор, и цикл "пока". Условный оператор выглядит следующим образом: если условие | то | последовательность действий 1 | иначе | последовательность действий 2 конец если Последовательность действий 1 выполняется, когда условие истинно; в противном случае выполняется последовательность действий 2. Ключевое слово "иначе" и последовательность действий 2 могут отсутствовать; в этом случае, когда условие ложно, исполнитель ничего не делает. Цикл "пока", или цикл с предусловием выглядит следующим образом: цикл пока условие | последовательность действий конец цикла Сначала проверяется условие в заголовке цикла. Если оно истинно, то выполняется последовательность действий, составляющая тело цикла. Это повторяется неограниченное число раз, пока условие истинно. Цикл заканчивается, когда условие при очередной проверке оказывается ложным. Важно отметить, что условие проверяется перед каждым выполнением тела цикла, но не в процессе его выполнения. Помимо элементарных действий, в записи алгоритма можно использовать другие алгоритмы. Также в записи алгоритма могут присутствовать комментарии, которые игнорируются исполнителем алгоритма. Для отделения комментария будут использоваться знаки // (двойная косая черта) для строчного комментария или /* …. */ для блока в соответствии с синтаксисом языка C++. 3.3. Язык схем Схемой называется наглядное графическое изображение алгоритма, когда отдельные действия (этапы) алгоритма изображаются при помощи различных геометрических фигур (блоков), а связи между этапами (последовательность выполнения этапов) указываются при помощи линий, соединяющих эти фигуры. Несмотря на все многообразие решаемых на ЭВМ задач, можно выделить несколько «типичных» действий (этапов), которые в различной последовательности выполняются при решении задач: 1.Присваивание является основной операцией, при помощи которой осуществляется обработка данных. 2.Проверка условия и выбор в зависимости от результата проверки одного из двух путей вычислительного процесса. 3.Ввод данных и вывод результата. 4.Начало и конец вычислительного процесса. Конкретные операции указаны внутри фигур в качестве примеров. Рассмотрим выполнение этих действий, а также функции других элементов схем, приведенных на рис.4.1. 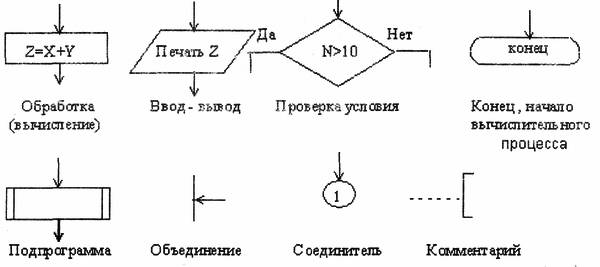 Рис. 4.1. основные элементы схем Присваивание. При выполнении операции присваивания переменной присваивается значение (переменная – некоторая величина, которая может изменяться, принимая в процессе этого изменения различные значения). Переменная обозначается при помощи имени. Именами обозначаются также различные функции (например, SIN). Функции имеют, в языках программирования, закрепленные за ними имена. Как Вы уже знаете, имя переменной обозначает символический адрес той ячейки памяти, в которой записано числовое значение соответствующей переменной или функции (после ее вычисления). Следовательно, термины "переменная" или "функция" только условно соответствуют общепринятым математическим понятиям. Числа, используемые, например, в операторах присваивания для задания значений переменных, называются константами. Константы обозначают сами числа, а не фактические адреса ячеек памяти. Оператор присваивания, обсуждающийся в этом разделе, используется только для выполнения арифметических операций, поэтому он называется арифметическим оператором присваивания. В языках программирования имеются и другие виды операторов присваивания. Арифметический оператор присваивания выполняет следующие действия. Операции, указанные справа от символа "=", выполняются над записанными в выражении константами (константа- величина, значение которой не изменяется в период ее существования) и теми числами, которые хранятся в ячейках памяти, обозначенных встречающимися именами. Результат помешается в ту ячейку памяти, символический адрес которой указан слева от символа "=". Говорят, что переменной присваивается значение посредством оператора присваивания. Следовательно, используемый здесь символ "=" (присвоить) имеет смысл, отличный от принятого в математике. Примеры операторов присваивания Оператор присваивания Действие оператора К=1 В ячейку памяти с символическим адресом К помещается 1. (переменной К присваивается значение 1) L=K В ячейку памяти с символическим адресом L пересылается содержимое ячейки с символическим адресом К (переменной L присваивается значение К). При этом К не изменяется. К=К+1 К содержимому ячейки с символическим адресом К прибавляется 1, результат помещается в ту же ячейку К. При этом старое значение К пропадает (стирается). Y=SIN(X) Вычисляется sin угла (выраженного в радианах), величина которого находится в ячейке X, и результат помещается в ячейку Y. X=SIN(X) Правая часть вычисляется аналогично. Значение функции записывается в ту же ячейку, в которой раньше находилось значение угла. Перед присваиванием старое значение пропадает (стирается). Замечания: 1. Перед выполнением присваивания старое значение переменной стирается. 2. При пересылке значение переменной копируется. Значение копируемой переменной не изменяется. 3. Переменным, которые располагаются в правой части оператора присваивания, должны быть присвоены определенные значения предшествующими операторами. 4. Если переменной не присвоено значение, то ее значение не определено. Проверка условия. Проверка условия является основой организации разветвлений, т. е. выбора одного из двух (или более) путей вычислительного процесса. Это этап принятия решения о дальнейшем ходе вычислительного процесса в зависимости от полученных промежуточных результатов. Имеется три вида разветвлений (см. ниже). Ввод-вывод данных. В операторах ввода-вывода записываются имена тех переменных, значения которых должны вводиться в оперативную память или выводиться из нее. В этих операторах могут быть указаны также внешние устройства, с которыми осуществляется обмен информацией. При вводе данные записываются в те ячейки памяти, символические адреса (имена) которых указаны в операторе. При выводе (печати) данных на экране (или бумаге) появляются значения, находящиеся в ячейках памяти, символические адреса которых перечислены в операторе вывода. Подпрограмма. Группу операторов, которые решают логически самостоятельную часть задачи, можно объединить в подпрограмму. Соединительные линии и их объединение. Все блоки схемы соединяются посредством линий, которые в сомнительных случаях снабжаются направляющими стрелками. Основными являются направления сверху вниз и слева направо. Объединение нескольких ветвей в одну ветвь обозначается точкой. Пересекающиеся линии без обозначения точки пересечения означают отсутствие соединений, по возможности следует избегать пересечений. Точками связи, или соединителями, пользуются в том случае, если соединительная линия не может быть доведена до следующего блока или до точки объединения. Тогда линия оканчивается соединителем, в котором записывается любой символ. Продолжением этой линии считается вторая точка связи, помеченная тем же символом. Комментарии можно записывать около любого блока. Содержание блоков не стандартизировано и зависит от степени детализации алгоритма. В частности, прямоугольник может быть использован для обозначения не только одной операции присваивания, но и более емких этапов преобразования (обработки) данных. Важно только, чтобы этот этап имел одного преемника, т. е. – чтобы после него выполнялся всегда один и тот же блок. При решении сложных задач обычно составляют несколько схем с различным уровнем детализации. Схема на каждом этапе разработки алгоритма должна давать наглядное представление об общей структуре алгоритма в целом или отдельных его частей. Схема не должна быть громоздкой, так как это приводит к потере наглядности, являющейся основным преимуществом схем, и не должна дублировать программу, изображая каждый оператор в виде отдельного блока. Последнее не относится к начинающим программистам. В частности, в настоящем пособии из дидактических соображений приводятся достаточно подробные схемы. 3.4. Основные структуры алгоритмов Основные структуры алгоритмов — это ограниченный набор стандартных способов соединения отдельных блоков или структур для выполнения типичных последовательностей действий. Приводимые ниже структуры рекомендуются при использовании так называемого структурного подхода к разработке алгоритмов и программ. Структурный подход предполагает использование только нескольких основных структур, комбинация которых дает все многообразие алгоритмов и программ. К основным структурам относятся (см. рис. 4.2): · следование а; · две разновидности цикла б, в; · три разновидности разветвления г, д, е. 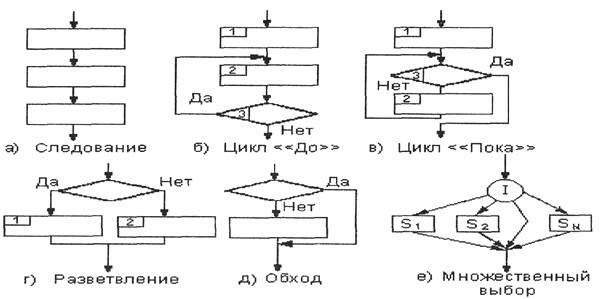 Рис.4.2. Основные структуры алгоритмов. Отметим вначале особенности трех основных типов структур. Следование – это последовательное размещение блоков и групп блоков, такая структура называется также линейной. Если некоторая часть программы (на схеме группа блоков) выполняется многократно и после проверки некоторого условия в какой-то момент осуществляется выход из нее, то такую часть называют циклом. Если после проверки некоторого условия выбирается один из двух (или более) путей вычислительного процесса и после выполнения любого из них вычислительный процесс опять сводится в одно русло, то возникает разветвление. Теперь рассмотрим особенности каждого вида цикла и разветвления. Цикл До. Применяется при необходимости выполнить какие-либо вычисления нескольких раз до выполнения некоторого условия (блок 3). Особенность этого цикла в том, что он всегда выполняется хотя бы один раз, так как первая проверка условия выхода из цикла происходит после того, как тело цикла выполнено. Тело цикла (блок 2) – это последовательность действий, которая выполняется многократно (в цикле). Начальные присвоения (блок 1) задание начальных значений тем переменным, которые используются в теле цикла. Цикл такого типа называют также итеративным циклом в том случае, когда количество повторений неизвестно до начала выполнения цикла. Цикл Пока. Отличается от цикла До тем, что проверка условия (блок 3) производится до выполнения тела цикла (блок 2), и, если при первой проверке условие выхода из цикла выполняется, то тело цикла не выполняется ни разу. Цикл такого типа называется также циклом по условию. Замечание. В некоторых случаях проверка условия осуществляется внутри тела цикла, т.е. тело цикла разбивается на две последовательности операторов: одна выполняется до проверки условия, вторая – после. Существует еще одна важная разновидность цикла: цикл по счетчику. Для него существует специальное обозначение и специальный оператор в различных алгоритмических языках программирования (оператор цикла). Для организации цикла по счетчику используется управляющая переменная цикла, изменяющаяся в заданных пределах с постоянным шагом. Разветвление применяется, когда в зависимости от условия нужно выполнить либо одно, либо другое действие. Действие 1 (блок 1) или действие 2 (блок 2) могут, в свою очередь, представлять собой одну из типовых структур. Обход – частный случай разветвления, когда одна ветвь не содержит никаких действий. Множественный выбор является обобщением разветвления, когда в зависимости от значения переменной (i) выполняется одно из нескольких действий. При i = 1 выполняется действие S1, при i = 2 – действие S2 и т. д. Особенностью всех приведенных структур является то, что они имеют один вход и один выход и их можно соединить друг с другом в любой последовательности. Каждая структура может также содержать в качестве одного из блоков любую другую структуру. Обычно при составлении схемы блоки размещаются друг под другом в порядке их выполнения. Возврат назад осуществляется только на циклах. Это дает простую и наглядную структуру алгоритма, по которой далее легко составлять программу. Если для разработки алгоритма используется метод пошаговой детализации, то первоначально продумывается и фиксируется общая структура алгоритма без детальной проработки отдельных его частей, но при этом также используются лишь основные структуры алгоритмов. Блоки, требующие дальнейшей детализации, обозначаются пунктирной линией. Далее прорабатываются (детализируются) отдельные блоки, не детализированные на предыдущем шаге, т.е. на каждом шаге разработки уточняется реализация фрагмента алгоритма (или программы), и, таким образом, на каждом шаге мы имеем дело с более простой задачей. Полностью закончив детализацию всех блоков, мы получим решение всей задачи в целом. В некоторых случаях, стремление, во что бы то ни стало, остаться в рамках структурного подхода приводит к необоснованному усложнению программы и потере ее наглядности и естественности. Если учесть, что структурное программирование имеет целью не подчинить программы каким-то правилам, а сделать их более удобными для восприятия, то в ряде случаев оказывается целесообразным отдать предпочтение ясности и естественности программы. Составим в качестве примера алгоритм вычисления суммы квадратов целых чисел от 1 до N (N не меньше 1,N должно быть задано перед выполнением программы или алгоритма.) 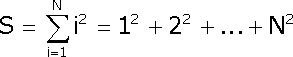 Такая сумма называется накапливающейся.
Рис. 4.3. Алгоритм вычисления суммы квадратов чисел от 1 до N 3.5. Понятие переменной Алгоритм состоит из команд исполнителю. Исполнитель может, в свою очередь, командовать другими исполнителями. Компьютер можно рассматривать как универсальный исполнитель, который управляет другими исполнителями. Рассмотрим, к примеру, автомобиль с инжекторным двигателем. В нем работой двигателя управляет компьютер (его иногда называют микропроцессорный блок). Компьютер получает данные от разнообразных датчиков (датчики положения коленчатого вала и дроссельной заслонки, температуры охлаждающей жидкости, скорости, детонации, кислорода и др.) и отдает приказания исполняющим системам двигателя - модулю зажигания, бензонасосу, форсункам двигателя, регулятору холостого хода, системе продувки адсорбера и т.д. Таким образом, и датчики, и исполняющие системы двигателя управляются компьютером, который выступает в роли универсального исполнителя. Запись алгоритма для универсального исполнителя может включать команды, адресованные ему непосредственно, а также команды, которые нужно передать подчиненным исполнителям. В чем разница между универсальным и простейшими подчиненными исполнителями? Как правило, универсальный исполнитель имеет собственную память, и выполнение им команд может приводить не к каким-либо внешним действиям, а к изменению его внутреннего состояния. Например, используя сигналы от датчика фазы, компьютер автомобиля вычисляет текущие обороты двигателя (которые показывает на тахометре). Используя эти данные и информацию, поступающую от датчика скорости автомобиля, компьютер может вычислить, какая передача включена в определенный момент времени. Далее вычисляется текущая нагрузка на двигатель и устанавливается, какой должна быть смесь бензина и воздуха, подаваемая в цилиндры двигателя. В зависимости от этого подаются команды на открытие форсунок. От степени обогащения смеси зависит момент зажигания - чем богаче смесь, тем позже момент зажигания; таким образом, подаче команды модулю зажигания предшествуют достаточно сложные вычисления. Таким образом, компьютер автомобиля, управляющий работой двигателя, хранит в любой момент времени в своей памяти текущие скорость, передачу, нагрузку на двигатель, температуру охлаждающей жидкости, требуемую степень обогащенности смеси и многие другие параметры. Эти параметры периодически перевычисляются на основании сигналов от разнообразных датчиков. В зависимости от значений параметров, компьютер передает те или иные сигналы управляющим системам двигателя. Значение каждого параметра хранится в определенном участке памяти компьютера и может меняться в процессе выполнения алгоритма. Такой участок памяти компьютера называется переменной. Понятие переменной - важнейшее понятие алгоритмического языка. Переменные встроены в конструкцию универсального исполнителя. Каждой переменной присваивается имя. В рассмотренном примере используются переменные "скорость", "обороты двигателя", "передача", "нагрузка", "температура", "обогащенность смеси", "угол опережения зажигания" и другие. С каждой переменной связан ее тип, т.е. множество значений, которое она может принимать. Например, "передача" принимает целые значения от 1 до 5 (обратная и первая передачи не различаются), тогда как "скорость", а также "обогащенность смеси" принимают вещественные значения (скорость измеряется в м/сек, обогащенность смеси может измеряться либо соотношением кислорода и паров бензина в единице объема, либо в процентах относительно стехиометрической смеси 14/1, соответствующей полному сгоранию паров бензина). С переменной можно выполнять два действия: 1. прочитать текущее значение переменной; 2. записать новое значение в переменную или, как говорят программисты, присвоить новое значение переменной. В алгоритмическом языке чтение значения переменной выполняется в результате использования ее имени в любом выражении. Запись нового значения переменной выполняется с помощью так называемого оператора присваивания. Он выглядит следующим образом: имя переменной = выражение; Знак = читается как присвоить значение. При выполнении оператора присваивания сначала вычисляется значение выражения в правой части, затем оно записывается в переменную, имя которой указано в левой части. Старое значение переменной при этом стирается. Например, скорость автомобиля вычисляется по количеству импульсов от датчика скорости в единицу времени: датчик скорости посылает 6 импульсов на каждый пройденный метр. скорость = число импульсов от датчика скорости); // (6 * интервал времени); Переменная "число импульсов от датчика скорости" в течение каждого интервала времени суммирует число импульсов. В начале каждого интервала она обнуляется. Полученная в результате скорость выражается в м/с. Если нужно получить скорость в км/час, то дополнительно выполняется следующее действие: скорость = скорость * 3600 / 1000; Здесь переменная "скорость" входит как в правую, так и в левую части оператора присваивания. В правой части используется старое значение этой переменной, вычисленное в м/сек. Поскольку час содержит 3600 секунд, то при домножении на 3600 получается расстояние в метрах, проходимое за 1 час; после деления на 1000 получается расстояние в километрах. Вычисленное значение затем присваивается переменной "скорость". Суммируем сказанное выше: 1. универсальный исполнитель, или компьютер, - это исполнитель, который может управлять другими исполнителями. Запись алгоритма для универсального исполнителя может включать команды, которые он должен передать подчиненным исполнителям, и команды, изменяющие внутреннее состояние самого универсального исполнителя; 2. внутреннее состояние универсального исполнителя определяется состоянием его памяти. Память - это материальный носитель (лента машины Тьюринга, ламповая или ферритовая память первых компьютеров, полупроводниковая память современных компьютеров), который хранит информацию. Эту информацию можно читать и перезаписывать; 3. переменная - это область памяти универсального исполнителя, хранящая порцию информации. Любая переменная имеет имя и тип. Тип переменной определяется множеством всех значений, которые она может принимать. Память универсального исполнителя можно рассматривать как набор переменных; 4. с переменной можно выполнять два действия: прочитать ее текущее значение и записать в нее новое значение (старое теряется). В алгоритмическом языке значение переменной читается, когда ее имя используется в любом выражении, значение которого надо вычислить. Для записи нового значения в переменную применяется оператор присваивания, который имеет вид: имя переменной = выражение; При его выполнении сначала вычисляется значение выражения справа от знака присваивания =, затем оно записывается в переменную. Выражение в правой части может включать имя переменной в левой части. В этом случае при вычислении выражения используется старое значение переменной. |