теория вероятности. Тест ТВиМС 300. Теория вероятности и математическая статистика 300
 Скачать 0.67 Mb.
|
|
Теория вероятности и математическая статистика 300 1.Вероятность невозможного события равна: 0 1 3 2 0,5 2. Производится 3 выстрела с вероятностями попадания в цель, равными 0,5, 0,5 и 0,3. Найти математическое ожидание общего числа попаданий. 1,3 0,9 1,7 1 2,3 3. Производится 4 выстрела с вероятностями попадания в цель  ,  ,  ,  . Найти математическое ожидание общего числа попаданий.2,2 1,9 1,7 2,6 2,3 4. Найти среднее квадратическое отклонение случайной величины Х, если дисперсия случайной величины Х равна 676. 26 12 63 35 38 5. Найти среднее квадратическое отклонение случайной величины Х, если дисперсия случайной величины Х равна 2,25. 1,5 1,1 1,2 1,3 1,7 6. Дано М(Х)=3 и М(Y)=4. Найти М(2Х-3Y). -6 -4 -8 -12 -10 7. Дано М(Х)=1 и М(Y)=7. Найти М(3Х+2Y). 17 37 21 11 23 8.В урне 10 шаров: 5 красных, 2 синих, 3 белый. Найти вероятность того, что извлеченный шар окажется красным? 0,5 0,9 0,7 0,3 0,1 9. Формула  - это формула …дисперсии квадратического отклонения математического ожидания моды медианы 10.Формула  - это формула …квадратического отклонения дисперсии математического ожидания моды медианы 11.  - это формула …математического ожидания НСВ дисперсии НСВ дисперсии ДСВ квадратического отклонения ДСВ математического отклонения ДСВ 12.Значение величины непрерывной случайной величины Х, плотность вероятности которого максимальна, называется … модой медианой биссектрисой гипотенузой ортом 13. Формула 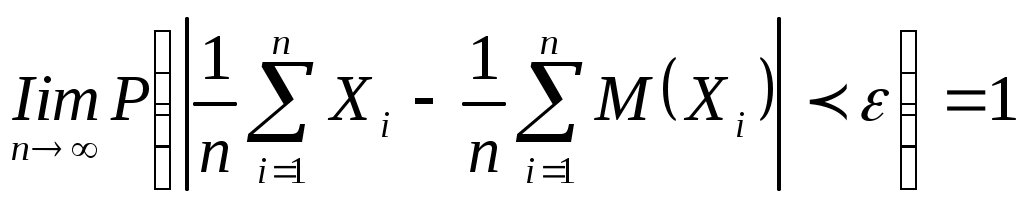 является ...теоремой Чебышева теоремой Колмогорова теоремой Менделеева теоремой Маркова теоремой Лебедева 14. Найти дисперсию случайной величины Х, если математическое ожидание квадрата случайной величины Х равно 54,8, а математическое ожидание случайной величины Х равно 6,3. 15,11 13,22 12,55 14,77 11,66 15. Найти дисперсию случайной величины Х, если математическое ожидание квадрата случайной величины Х равно 81,54, а математическое ожидание случайной величины Х равно 7,8. 20,7 21,5 22,6 23,4 24,1 16.Какова вероятность достоверного события? 1 0 0,2 0,4 0,5 17. Математические ожидания случайных величин Х и Y равны соответственно 4 и 3. Найти математическое ожидание случайной величины 7Х+3Y. 37 39 15 31 37 18. Математические ожидания случайных величин Х и Y равны соответственно 4 и 3. Найти математическое ожидание случайной величины 9Х+4Y. 48 24 35 36 40 19.Монета брошена два раза. Найти вероятность того, что хотя бы один раз появится «герб». 0,75 0,5 0,15 0,1 0,2 20.Закон распределения величины Х известен:
|