теория вероятности. Тест ТВиМС 300. Теория вероятности и математическая статистика 300
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
Найти 0,16 0,15 0,18 0,13 0,12 51. Для некоторой местности средние число пасмурных дней в сентябре равно 8. Найти вероятность того, что первого сентябре будет ясная погода. 22/30 3/31 7/25 8/30 25/30 52. Дана Х дискретная случайная величина. Найти D(X), если M(x 6 8 3 2 4 53. Дана Х дискретная случайная величина. Найти D(X), если M(x 21 13 17 25 11 54. Найти D(X), если M(x 26 25 13 10 21 55. События А, В, С, Д, Е, образуют полную группу событий, причем 56. Два стрелка независимо друг друга стреляют по цели. Вероятность попадения в цель для первого стрелка равна 0,4, для второго равна 0,3. Какова вероятность того, что цель будет поражена. 0,12 0,84 0,18 0,14 0,6 57. В ящике содержится 4 белых, 5 красных и 6 черных шаров. Из урны вынули случайно один шар. Какова вероятность того, что полученный шар красный? 1/3 1/4 2/3 1 1/5 58. Вероятность появления бракованной детали в парти равно 0,015. Найти вероятность того, что из этой партии будет изъята небракованная деталь. 0,985 0,885 0,785 0,685 0,585 59. Какова вероятность того, что при одном бросании игральной кости выпадает не 6 очков? 5/6 1/6 4/6 2/6 3/4 60. Вероятность выигрыша, приходящаяся на один билет в школьной лотерее, равна 0,03. Какова вероятность получения невыигрышного билета в этой лотерее? 0,97 0,87 0,77 0,67 0,57 61. Брошены 2 игральные кости. Какова вероятность того, что на обеих костях не выпало по 3 очка. 35/36 31/36 29/36 27/36 13/36 62. Формула A.математического ожидания B.математического анализа C.математического сложения D.математического умножения E.математического дифференцирования 63. В одном мешке находится 3 красных шара и 2 синих, в другом мешке - 2 красных и 3 синих. Из каждого мешка наугад вынимают по одному шару. Какова вероятность того, что оба шара окажутся красными? 6/25 4/25 3/25 2/25 7/25 64. Монету бросают три раза подряд. Какова вероятность того, что каждый раз выпадает решка? 1/8 1/7 1/9 1/6 3/8 65. Вероятность остоновки за смену одного станка, работающего в цехе, равна 0,15, а другого- 0,16. Какова вероятность того, что оба станка за смену не остановятся? 0,714 0,814 0,614 0,514 0,914 66. Вероятность выигрыша, приходящаяся на один билет в школьной лотерее, равна 2/121. Какова вероятность получения невыигрышного билета в этой лотерее? 119/121 113/121 117/121 116/121 115/121 67. В яшике лежать 3 белых, 4 черных и 5 красных шаров. Какова вероятность того, что наугад вынутый шар окажется не белым? 3/4 1/4 3/5 3/7 1/5 68. В яшике лежать 3 белых, 4 черных и 5 красных шаров. Какова вероятность того, что наугад вынутый шар окажется не черным? 2/3 1/3 1/2 1 3/4 69. В яшике лежать 3 белых, 4 черных и 5 красных шаров. Какова вероятность того, что наугад вынутый шар окажется не красным? 7/12 5/12 1/4 1/3 3/4 70. Для украшениея елки принесли коробку, в которой находится 10 красных, 7 зеленых, 5 синих и 8 золотых шаров. Из коробки наугад вынимают один шар. Какова вероятность того, что он окажется красным. 1/3 4/15 3/5 2/5 2/15 71. Для украшениея елки принесли коробку, в которой находится 10 красных, 7 зеленых, 5 синих и 8 золотых шаров. Из коробки наугад вынимают один шар. Какова вероятность того, что он окажется золотым. 4/15 3/4 3/5 2/5 2/11 72. Для украшениея елки принесли коробку, в которой находится 10 красных, 7 зеленых, 5 синих и 8 золотых шаров. Из коробки наугад вынимают один шар. Какова вероятность того, что он окажется красным или золотым. 3/6 3/4 3/5 2/5 2/15 73. В одной партии электролампочек 3 % бракованных, а в другой 4 % бракованных. Наугад берут по одной лампочке из каждой партии. Какова вероятность того, что обе лампочки окажется бракованными? 0,0012 0,0013 0,0011 0,0016 0,0014 74. На одной полке стоит 12 книг, две из которых сборники стихов, а на другой 15 книг, три из которых сборники стихов. Наугад берут с каждой полки по одной книге. Какова вероятность того, что обе книги окажутся сборниками стихов? 1/30 1/20 1/10 1/40 1/50 75. В мешке находится 5 белых шаров и 3 черных. Из мешка наугад вынимают один шар. Его цвет записывают, записивают, шар возвращают в мешок и шары перемешивают. Затем снова из мешка вынимают один шар. Какова вероятность того, что оба раза будут вынуты белые шары? 25/64 9/64 27/64 23/64 21/64 76. В мешке находится 5 белых шаров и 3 черных. Из мешка наугад вынимают один шар. Его цвет записывают, записивают, шар возвращают в мешок и шары перемешивают. Затем снова из мешка вынимают один шар. Какова вероятность того, что оба раза будут вынуты черные шары? 9/64 25/64 27/64 23/64 21/64 77. Женщина в поисках необходимой вещи зашла в 3 магазина. Вероятность того, что она купит необходимую вещь в первом магазине равна 0,6, во втором – 0,7, а в третьем – 0,5. Какова вероятность того, что вещь будет куплена в этих магазинах? 0,21 0,22 0,43 0,23 0,25 78. В классе 12 мальчиков, 18 девочек. В состав делегации необходимо выбрать двух учащихся. Какова вероятность того, что наугад выберут одного мальчика и одну девочку? 72/145 71/145 73/175 70/145 78/175 79. Два стрелка независимо друг от друга выстрелили в мишень. Вероятность попадания в цель первого стрелка равна 0,75, а второго - 0,8. Найти вероятность того, что хотя бы один стрелок попадет точно в цель. 0,35 0,85 0,75 0,95 0,55 80. Для разрушения моста достаточно одной авиабомбы. На мост скинули 4 авиабомбы, вероятность их попадания точно в цель равна соответственно: 0,3; 0,4; 0,6, и 0,7. Найти вероятность разрушения моста. 0,9496 0,9492 0,7496 0,6496 0,5496 81. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра. 1/10 1/100 3/10 7/10 9/10 82. Набирая номер телефона, абонент забыл последние две цифры и помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры. 1/90 1/80 3/40 7/50 9/60 83. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого, наудачу извлеченного жетона, не содержит цифры 5. 0,81 0,71 0,91 0,61 0,51 84. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара. 1/2 1/3 1/4 1/5 1/6 85. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую 0,35. Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область. 0,8 0,7 0,6 0,5 0,4 86. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2 деталей есть хотя бы одно стандартная. 44/45 43/45 41/45 39/45 42/45 87. События А, В, С и Д образует полную систему. Вероятности событий таковы: Р(А)=0,1; Р(В)=0,4; Р(С)=0,3. Чему равна вероятность события Д? Р(Д)=0,2 Р(Д)=0,3 Р(Д)=0,1 Р(Д) =0,4 Р(Д)=0,5 88. Найти вероятность совместного появления герба при одном бросании двух монет. 1/4 1/3 1/2 1/5 1/6 89. Вероятность попадания в цель при стрельбе из трех орудий таковы: Р1=0,8; Р2=0,7; Р3=0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий. 0,496 0,884 0,794 0,694 0,594 90. Вероятность попадания в цель при стрельбе первого и второго орудий соответственно равны: Р1=0,7; Р2=0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одном из орудий. 0,44 0,84 0,74 0,64 0,56 91. Два стрелка произвели по одному выстрелу. Вероятность попадания в мишен первым стрелком равна 0,7, а вторым - 0,6. Найти вероятность того, что хотя бы один из стрелков попал в мишек. 0,58 0,98 0,78 0,68 0,48 92. Возможные значения случайной величины таковы: х1=2, х2=5, х3=8. Известны вероятности первых двух возможных значений: Р1=0,4; Р2=0,15. Найти вероятность х3. Р3=0,45 Р3=0,55 Р3=0,35 Р3=0,65 Р3=0,25 93. Производится 3 выстрела с вероятностями попадания в цель, равными Р1=0,4; Р2=0,3 и Р3=0,6. Найти математическое ожидание общего числа попаданий. 2,8 1,2 1,4 1,5 1,1 94. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей. 7 6 8 5 4 95. Вероятность попадания в цель при стрельбе из орудия Р=0,6. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов. 6 5 4 7 8 96. Производится 4 выстрела с вероятностями попадания в цель Р1=0,1; Р2=0,2, Р3=0,5 и Р4=0,2. Найти математическое ожидание общего числа попаданий. 2,8 1,2 3,2 4,2 2,2 97. События А; В; С и Д образуют полную систему. Вероятности событий таковы Р(А)= 0,1; Р(В)=0,4; Р(С)=0,3. Чему равна вероятность события Д? Р(Д)=0,2 Р(Д)=0,3 Р(Д)=0,1 Р(Д)=0,4 Р(Д)=0,5 98. Формула дисперсии подобия симметрии цикличности дивергенции 99. Формула локальная теорема Лапласа производная теорема Байеса предельная теорема Коши интегральная теорема Безу подынтегральная теорема Лейбница 100. Лапласа Безу Даламбера Лейбница Коши 101. Дисперсия дискретной случайной величины равна 6,25. Найти среднеквдратичное отклонение. 2,5 1,5 3,5 0,5 4,5 102. События А; В; С и Д образуют полную систему. Вероятности событий таковы Р(А)= 0,1; Р(В)=0,1; Р(С)=0,1. Чему равна вероятность события Д? Р(Д)=0,7 Р(Д)=0,3 Р(Д)=0,1 Р(Д)=0,4 Р(Д)=0,2 103. События А; В; С и Д образуют полную систему. Вероятности событий таковы Р(А)= 0,2; Р(В)=0,3; Р(С)=0,2. Чему равна вероятность события Д? Р(Д)=0,3 Р(Д)=0,5 Р(Д)=0,1 Р(Д)=0,4 Р(Д)=0,2 104. События А; В; С и Д образуют полную систему. Вероятности событий таковы Р(А)= 0,3; Р(В)=0,3; Р(С)=0,3. Чему равна вероятность события Д? Р(Д)=0,1 Р(Д)=0,3 Р(Д)=0,5 Р(Д)=0,4 Р(Д)=0,2 105. Вероятность выигрыши, приходящаяся на один билет в школьной лотер равно 0,03. Какова вероятность получения невыигрышеного билета в этой лотерее. 0,97 0,87 0,77 0,67 0,57 106. Вероятность выигрыши, приходящаяся на один билет в школьной лотер равно 0,13. Какова вероятность получения невыигрышеного билета в этой лотерее. 0,87 0,97 0,77 0,67 0,57 107. Вероятность выигрыши, приходящаяся на один билет в школьной лотер равно 0,33. Какова вероятность получения невыигрышеного билета в этой лотерее. 0,67 0,87 0,77 0,97 0,57 108. Вероятность выигрыши, приходящаяся на один билет в школьной лотер равно 0,23. Какова вероятность получения невыигрышеного билета в этой лотерее. 0,77 0,87 0,97 0,67 0,57 109. Вероятность выигрыши, приходящаяся на один билет в школьной лотер равно 0,43. Какова вероятность получения невыигрышеного билета в этой лотерее. 0,57 0,87 0,77 0,67 0,97 110. В одном мешке находится 3 красных шара и 2 синих, в другом мешке - 2 красных и 3 синих. Из каждого мешка наугад вынимают по одного шару. Какова вероятность того, что оба шара окажутся красными. 6/25 4/25 6/25 2/25 7/25 111. В одном мешке находится 4 красных шара и 5 синих, в другом мешке - 5 красных и 4 синих. Из каждого мешка наугад вынимают по одного шару. Какова вероятность того, что оба шара окажутся красными. 20/81 4/81 6/81 20/25 7/65 112. В одном мешке находится 3 красных шара и 2 синих, в другом мешке - 2 красных и 3 синих. Из каждого мешка наугад вынимают по одного шару. Какова вероятность того, что оба шара окажутся синими. 6/25 4/25 6/25 2/25 7/25 113. В одном мешке находится 4 красных шара и 5 синих, в другом мешке - 5 красных и 4 синих. Из каждого мешка наугад вынимают по одного шару. Какова вероятность того, что оба шара окажутся синими. 20/81 4/81 6/81 20/25 7/65 114. Вероятность выигрыша, приходящаяся на один билет в школьной лотерее, равна 2/11. Какова вероятность получения невыгрышного билета в этой лотерее. 9/11 11/12 7/11 6/11 5/11 115. События А; В; С и Д образуют полную систему. Вероятности событий таковы Р(А)= 0,2; Р(В)=0,3; Р(С)=0,3. Чему равна вероятность события Д? Р(Д)=0,2 Р(Д)=0,3 Р(Д)=0,1 Р(Д)=0,4 Р(Д)=0,5 116. В вазе 3 белых розы, 3 красных розы, 3 тюльпана, 7 гвоздик и 5 белых лилий. Какова вероятность того, что наугад вынутый цветок окажется тюльпаном? 1/7 3/14 3/5 2/9 1/8 117. В вазе 3 белых розы, 3 красных розы, 3 василька, 7 гвоздик и 5 белых лилий. Какова вероятность того, что наугад вынутый цветок окажется тюльпаном? 0 1 3/5 2/9 1/8 118. В вазе 3 белых розы, 3 красных розы, 3 тюльпана, 3 гвоздик и 7 белых лилий. Какова вероятность того, что наугад вынутый цветок окажется белой розой? 3/19 5/14 3/15 3/17 5/18 119. В вазе 3 белых розы, 3 желтых тюльпана, 5 гвоздик, 9 астры и 1 белая лилия. Какова вероятность того, что наугад вынутый цветок окажется гвоздикой? 5/21 5/14 5/19 5/22 5/18 120. В ящике лежат 3 белых, 4 черных и 5 красных шаров. Какова вероятность того, что наугад вынутый шар окажется не черным? 8/12 5/14 3/15 3/17 4/12 121. В ящике лежат 3 белых, 4 черных и 5 красных шаров. Какова вероятность того, что наугад вынутый шар окажется не красным. 7/12 1/4 3/5 1/3 1/5 122. Найти М(2X+3У), если М(Х)=4, M(Y)=5,5. 24,5 24 22,5 20,5 26 123. События А, В, С, Д, Е, образуют полную группу событий, причел P(A)=0.2; p(B)=0.1; p(C)=0.25; p(D)=0.15. Найти p(E)=? Р(Е)=0,3 P(Е)=0,1 P(Е)=0,2 P(Е)=0,7 P(Е)=0,5 124. В ящике содержится 4 белых, 5 красных и 6 черных шаров. Из урны вынули случайно один шар. Какова вероятность того, что полученный шар красный. 1/3 1/5 2/3 1 1/4 125. События А, В, С, Д, Е, образуют полную группу событий, причел P(A)=0.25; p(B)=0,15; p(C)=0.25; p(D)=0,15. Найти p(E)=? Р(Е)=0,2 P(Е)=0,1 P(Е)=0,3 P(Е)=0,7 P(Е)=0,5 126. События А,В,С,Д,Е, образуют полную группу событий, причел P(A)=0,2; p(B)=0,1; p(C)=0,2; p(D)=0,5. Найти p(E)=? Р(Е)=0 P(Е)=0,1 P(Е)=0,2 P(Е)=0,7 P(Е)=0,5 127. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара. 1/2 1/3 1/4 1/5 1/6 128. Случайная величина распределена следующим законом: X P Найти.P 0,15 0,2 0,05 0 0,1 129. В ящике имеется 6 белых и 4 красных шаров. Какова вероятность того, наудачу вынутый шар окажется белым. 3/5 5/9 4/9 2/5 4/5 130. В ящике имеется 6 белых и 4 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется красным. 2/5 5/9 4/9 3/5 4/5 131. В коробке имеется 10 белых и 15 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется красным. 2/5 5/9 4/9 3/5 4/5 132. В ящике имеется 4 белых, 6 желтых и 10 красных шаров. Какова вероятность того что, наудачу вынутый шар окажется белым. 1/5 1/3 4/5 3/4 4/9 133. В ящике имеется 4 белых, 6 желтых и 10 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется желтым. 3/10 1/3 4/5 3/20 4/9 134. В мешке имеется 4 белых, 6 желтых и 10 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется красным. 1/2 1/3 4/5 3/20 4/9 135. В коробке 10 белых и 15 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется белым. 2/5 5/9 4/9 3/5 4/5 136. Студент подготовил 40 из 50 вопросов экзамена по предмету. Найти вероятность того, что он знает оба вопроса билета? 156/245 7/550 5/4 3/8 52/68. 137. Задумано число от 1 до 10. Найти вероятность того, что задуманным числом окажется четное число. 1/2 1/9 1/10 1/5 1/8 138. В группе 8 студентов, среди которых 4 мальчика. По списку отобраны 3 студента. Найти вероятность того, что среди отобранных студентов окажутся 2 мальчика. 3/14 1/2 5/6 1/24 1/7 139. В группе 8 студентов, среди которых 4 мальчика. По списку отобраны 3 студента. Найти вероятность того, что среди отобранных студентов окажутся 2 девочки. 3/14 1/2 1/5 1/24 1/7 140. P Бернулли Лагранжа Лапласа Пуассона Байеса 141. Найти формулу Пуассона: 142. Найти формулу Бернулли: 143. Дано: D(х)=2 и D(y)=3. Вычислить D(3Х – 2У). 30 64 94 14 82 144. Дано: D(х)=5 и D(y)=9. Вычислить D(3Х – 2У). 81 64 88 114 96 145. Дано: D(х)=3 и D(y)=7. Вычислить D(3Х – 2У). 55 65 95 45 85 146. Дано: D(х)=4 и D(y)=8. Вычислить D(3Х – 2У). 68 64 90 14 82 147. Дано: D(х)=5 и D(y)=4. Вычислить D(3Х – 2У). 61 63 65 67 69 148. Дано: D(х)=4 и D(y)=5. Вычислить D(3Х – 2У). 56 64 94 44 78 149. Дано: D(х)=5 и D(y)=3. Вычислить D(3Х – 2У). 57 63 91 41 83 150. Дано: D(х)=2 и D(y)=5. Вычислить D(3Х – 2У). 38 64 88 24 78 151. Дано: D(х)=6 и D(y)=7. Вычислить D(3Х – 2У). 82 64 90 74 68 152. Дано: D(х)=7 и D(y)=5. Вычислить D(3Х – 2У). 85 65 95 45 75 153. Укажите формулу полной вероятности: Р(А)= Р(А)=Р(А Р(А)=Р(В) Р(А+В+С)=Р(А)+ Р(А)+Р(В)=1 154. Чему равна сумма вероятностей событий, образующих полную группу? 1 0 0 p<0 155. Математические ожидания случайных величин Х и Y равны соответственно 4 и 7. Найти математическое ожидание случайной величины 5Х–2Y. 6 8 4 10 2 156. Математические ожидания случайной величины Х равно 7. Найти математическое ожидание случайной величины 8Х-2. 54 65 16 76 62 157. Дисперсии случайных величин Х и Y равны соответственно 5 и 9. Найти дисперсию случайной величины 4Х-3Y 161 162 160 163 164 158. Вероятность появления шести очков равна 1/6. Найти вероятность не появления шести очков: 5/6 1/3 3/4 5/3 1/5 159. Математические ожидания случайных величин Х и Y равны соответственно 4 и 3. Найти математическое ожидание случайной величины 8Х-3Y. 23 9 15 6 7 160. Что называется случайным событием? Явление, которое может произойти, а может и не произойти. Несовместные явления. Появление противоположного события. Явление, которое обязательно должно произойти. Нет правильного ответа. 161. Отношение числа благоприятствующих случаев события А к числу возможных исходов событий называется ... Вероятностью события А Относительной частотой события А Событие А Статистической вероятностью события А Произведением событий 162. Два события, образующих полную группу, называются ... Противоположными событий Несовместными событиями Суммой событий Произведением событий Равными событиями 163.На пяти карточках написаны буквы О,П,Р, С,Т. Тщательно перемешав карточки, извлекают их по одной и располагают в порядке извлечения. Определить вероятность того, что получится слово СПОРТ. 1/120 2/57 1/90 3/40 5/111 164.Вероятность попадания первого стрелка в цель равна 0,7, а второго 0,9. Найти вероятность того, что оба стрелка попадут в цель. 0,63 0,81 0,9 1 0,6. 165.Один из трех стрелков вызывается на линию огня и производит 2 выстрела. Вероятность попадания при одном выстреле в мишень для первого, второго и третьего стрелков соответственно равны 0,4; 0,6; 0,8. Найти вероятность того, что в мишени будет два пробела. 0,464 0,469 0,446 0,448 0,465 166.В урне 9 белых и 1 черный шар. Вынули сразу 3 шара. Какова вероятность того, что все шары белые? 7/10 5/9 4/5 2/3 3/8 167.Найдите формулу с помощью которой находится число перестановок из n элементов: 168.Найдите формулу с помощью которой находится число размешений из n элементов по k элементов: 169.Найдите формулу с помощью которой находится число сочетаний из n элементов по k элементов: 170.Показать формулу сочетания из n элементов по m: 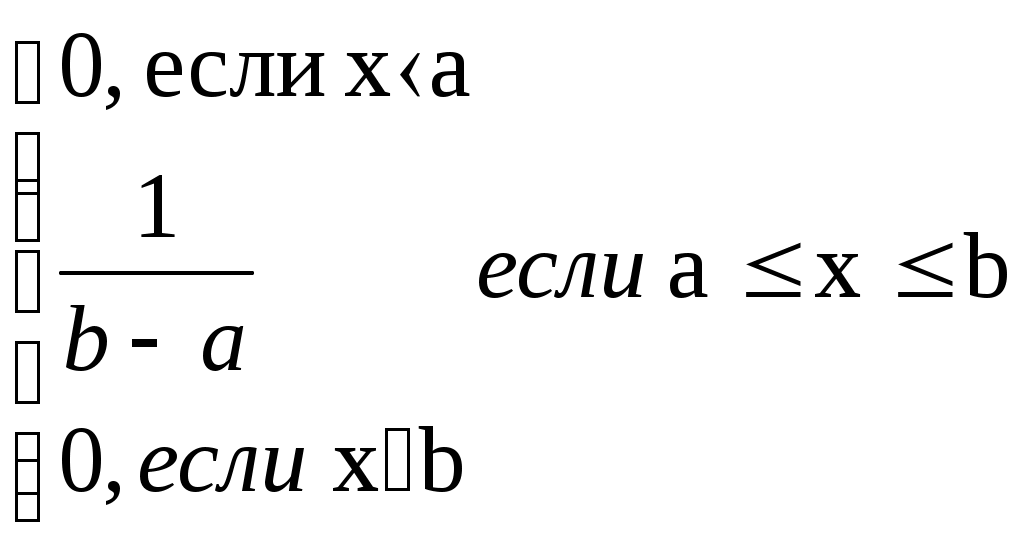 C q 171.Показать формулу вероятности произведения независимых событий. 172. Формула A. дисперсии B.подобия C.симметрии D.цикличности E.дивергенции 173. Формула A.средней B.подобия C.симметрии D.цикличности E.дивергенции 174.На шести карточках написаны буквы А,А,Ы,Т,Л,М; тщательно перемешав карточки, извлекают их по одной и располагают в порядке извлечения. Определить вероятность того, что получится слово «АЛМАТЫ». 1/720 1/620 1/520 1/820 1/920 175.Показать формулу вероятности произведения зависимых событий. 176.Вероятность выигрыша, приходящаяся на один билет в школьной лотерее, равна 2/9. Какова вероятность получения невыгрышного билета в этой лотерее. 7/9 2/9 1/9 4/9 5/9 177.В сумке лежат 6 белых, 4 черных и 5 красных шаров. Какова вероятность того, что наугад вынутый шар окажется не белым. 3/5 1/5 2/5 4/5 1 178.В коробке лежат 6 белых, 4 черных и 5 красных шаров. Какова вероятность того, что наугад вынутый шар окажется не черным. 11/15 3/5 4/3 1 3/4 179.В ящике лежат 6 белых, 4 черных и 5 красных шаров. Какова вероятность того, что наугад вынутый шар окажется не красным. 2/3 1/3 1/2 1 3/4 180.Вероятность выигрыша, приходящаяся на один билет в школьной лотерее, равна 2/7. Какова вероятность получения невыгрышного билета в этой лотерее. 5/7 2/7 1/7 4/7 3/7 181.Показать формулу Бейеса. 182.Игральная кость брошена. Найти вероятность того, что выпавших очков четная. 1/2 2/3 5/6 1/3 1/6 183.Показать формулу полной вероятности. 184.В урне имеется 4 белых и 5 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется белым. 4/9 5/9 2/9 1 4/5 185.В урне имеется 4 белых и 5 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется красным. 5/9 4/9 0 2/9 4/5 186.В урне имеется 4 белых, 3 желтых и 5 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется белым. 1/3 1/4 4/5 3/4 4/9 187.В урне имеется 4 белых, 3 желтых и 5 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется желтым. 1/4 1/3 1/5 3/4 4/9 188.В урне имеется 4 белых, 3 желтых и 5 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется красным. 5/12 1/4 4/5 5/9 4/9 189.Игральная кость брошена 2 раза. Найти вероятность того, что сумма выпавших очков равна 7. 1/6 1/5 1/4 1/3 1/10 190.Игральная кость брошена 2 раза. Найти вероятность того, что сумма выпавших очков равна 5. 1/9 1/5 1/4 1/6 1/2 191.Игральная кость брошена 2 раза. Найти вероятность того, что сумма выпавших очков равна 10. 1/9 1/5 1/12 1/3 1/2 192.Игральная кость брошена 2 раза. Найти вероятность того, что сумма выпавших очков равна 3. 1/18 1/12 1/4 1/3 1/2 193.Игральная кость брошена 2 раза. Найти вероятность того, что сумма выпавших очков равна 4. 1/9 1/5 1/14 1/15 1/2 194.Игральная кость брошена 2 раза. Найти вероятность того, что сумма выпавших очков равна 6. 1/6 4/5 2/3 7/36 5/12 195.Если в группе 9 студентов, то сколькими способами можно создать актив группы состоящий из 3 - х студентов? 84 94 36 120 54 196.В урне имеется 4 белых, 6 желтых и 5 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется белым. 4/15 1/15 6/15 5/15 4/9 197.В урне имеется 4 белых, 6 желтых и 5 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется желтым. 2/5 1/3 1/5 3/4 4/9 198.В урне имеется 4 белых, 6 желтых и 5 красных шаров. Какова вероятность того, что наудачу вынутый шар окажется красным. 1/3 1/4 4/5 5/9 4/9 199.Вероятность выиграть в шахматы равна 0,75. Найти вероятность проигрыша. 0,25 0,3 0,7 0,75 0 200. Дискретная случайная величина Х задана законом распределения:
|
