|
|
Культ. Тест 1 Вопрос 1
Тест 3
Вопрос №1
V1
|
Cистема линейных уравнений в матричном виде?
|
0
|
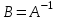
|
0
|
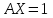
|
0
|
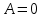
|
1
|
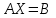
|
0
|
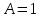
|
Вопрос №2
V1
|
Метод решения системы линейных уравнений, где посредством последовательного исключения неизвестных с помощью элементарных преобразований данная система уравнений приводится к эквивалентной ступенчатой системе, называется …..
|
1
|
Метод Гаусса
|
0
|
Метод Крамера
|
0
|
Метод обратной матрицы
|
0
|
Метод Даламбера
|
0
|
Метод Коши
|
Вопрос №3
V1
|
Чтобы система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы. Это теорема называется теоремой…..
|
0
|
Крамера
|
0
|
Гаусса
|
1
|
Кронекера-Капелли
|
0
|
Даламбера
|
0
|
Коши
|
Вопрос №4
Вопрос №5
Вопрос №6
Вопрос №7
Вопрос №8
Вопрос №9
Вопрос №10
V1
|

|
0
|
x=0, y= -1
|
1
|
x=1, y=2
|
0
|
x=0, y= -2
|
0
|
x=1, y= -2
|
0
|
x=2, y=3
|
Тест 4
Вопрос №1
V1
|
Коллинеарные вектора – это …
|
0
|
вектора, расположенные на пересекающихся прямых
|
1
|
вектора, расположенные на параллельных или совпадающих прямых
|
0
|
два вектора, не расположенные на одной прямой
|
0
|
вектора, расположенные на одной плоскости
|
0
|
непересекающиеся прямые
|
Вопрос №2
V1
|
Найти модуль вектора 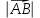 , если А(3;-2; 1), В(4; 1; 0) , если А(3;-2; 1), В(4; 1; 0)
|
0
|

|
1
|
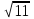
|
0
|
3
|
0
|
11
|
0
|
14
|
Вопрос №3
V1
|
Найти направляющий косинус 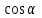 вектора вектора 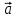 с координатами с координатами 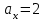 , , 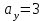 , , 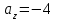 . .
|
0
|
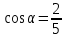
|
1
|
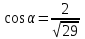
|
0
|
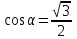
|
0
|
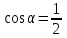
|
0
|
30
|
Вопрос №4
V1
|
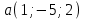 , , 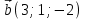 . Найдите векторное произведения . Найдите векторное произведения 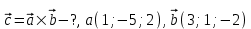
|
0
|
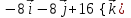
|
1
|
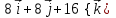
|
0
|
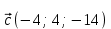
|
0
|
(-2, -8, 16)
|
0
|
(8, -8, 1)
|
Вопрос №5
V1
|
Найти значение m, при котором вектора 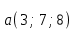 , , 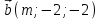 будут перпендикулярны. будут перпендикулярны.
|
0
|
11
|
1
|
10
|
0
|
-10
|
0
|
-11
|
0
|
12
|
Вопрос №6
V1
|
При каком значении m вектора 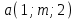 , , 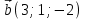 , , 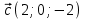 компланарны? компланарны?
|
0
|
2
|
0
|
1
|
0
|
0
|
1
|
3
|
0
|
8
|
Вопрос №7
|
|
|
 Скачать 0.56 Mb.
Скачать 0.56 Mb.