|
|
Тест Центральные и вписанные углы. Теорема о пересекающихся хордах (8 класс). Тест Вписанные и центральные углы. Теорема о пересекающихся хорд. Тест Центральные и вписанные углы. Теорема об отрезках пересекающихся хорд
ТЕСТ «Центральные и вписанные углы. Теорема об отрезках пересекающихся хорд»
ФИ____________________________ Класс_____________
Вариант 1
1. Центральный угол – это угол
А) сторона, которого проходит через центр окружности;
Б) вершина, которого лежит в центре окружности;
В) вершина, которого лежит на окружности.
2. Угол, вершина которого лежит на окружности, а стороны пересекают окружность называется
А) центральным; Б) вписанным; В) описанным.
3. Вписанный угол равен
А) двойной величине дуги, на которую он опирается;
Б) дуге, на которую он опирается;
В) половине дуги на которую он опирается.
4. Центральный угол равен
А) половине дуги, на которую он опирается.
Б) дуге, на которую он опирается;
В) удвоенной величине дуги, на которую он опирается;
5. Если две хорды окружности пересекаются, то
А) хорды равны
Б) Сумма отрезков одной хорды равна сумме отрезков другой
В) Произведение отрезков одной хорды равно произведению отрезков другой
6. Чему равен вписанный угол, опирающийся на дугу в 1000
А) 500; Б) 1000; В) 2000.
7.Чему равен центральный угол, опирающийся на дугу в 800
А) 1600; Б) 800; В) 400.
|
ТЕСТ «Центральные и вписанные углы. Теорема об отрезках пересекающихся хорд»
ФИ____________________________ Класс_____________
Вариант 2
1. Угол, вершина которого лежит в центре окружности называется
А) центральным; Б) вписанным; В) описанным.
2. Вписанный угол – это угол
А) сторона, которого проходит через центр окружности;
Б) вершина, которого лежит в центре окружности;
В) вершина, которого лежит на окружности, а стороны пересекают окружность
3. Вписанный угол равен
А) дуге, на которую он опирается;
Б) удвоенной величине дуги, на которую он опирается;
В) половине дуги на которую он опирается.
4. Центральный угол равен
А) двойной величине дуги, на которую он опирается;
Б) дуге, на которую он опирается;
В) половине дуги, на которую он опирается.
5. Если две хорды окружности пересекаются, то
А) Сумма отрезков одной хорды равна сумме отрезков другой
Б) Произведение отрезков одной хорды равно произведению отрезков другой
В) хорды равны
6. Чему равен вписанный угол, опирающийся на дугу в 1200
А) 1200; Б) 600; В) 2400
7. Чему равен центральный угол, опирающийся на дугу в 400
А) 800; Б) 200; В) 400
|
ТЕСТ «Центральные и вписанные углы. Теорема об отрезках пересекающихся хорд»
ФИ____________________________ Класс_____________
Вариант 1
1. Центральный угол – это угол
А) сторона, которого проходит через центр окружности;
Б) вершина, которого лежит в центре окружности;
В) вершина, которого лежит на окружности.
2. Угол, вершина которого лежит на окружности, а стороны пересекают окружность называется
А) центральным; Б) вписанным; В) описанным.
3. Вписанный угол равен
А) двойной величине дуги, на которую он опирается;
Б) дуге, на которую он опирается;
В) половине дуги на которую он опирается.
4. Центральный угол равен
А) половине дуги, на которую он опирается.
Б) дуге, на которую он опирается;
В) удвоенной величине дуги, на которую он опирается;
5. Если две хорды окружности пересекаются, то
А) хорды равны
Б) Сумма отрезков одной хорды равна сумме отрезков другой
В) Произведение отрезков одной хорды равно произведению отрезков другой
6. Чему равен вписанный угол, опирающийся на дугу в 1000
А) 500; Б) 1000; В) 2000.
7.Чему равен центральный угол, опирающийся на дугу в 800
А) 1600; Б) 800; В) 400.
|
ТЕСТ «Центральные и вписанные углы. Теорема об отрезках пересекающихся хорд»
ФИ____________________________ Класс_____________
Вариант 2
1. Угол, вершина которого лежит в центре окружности называется
А) центральным; Б) вписанным; В) описанным.
2. Вписанный угол – это угол
А) сторона, которого проходит через центр окружности;
Б) вершина, которого лежит в центре окружности;
В) вершина, которого лежит на окружности, а стороны пересекают окружность
3. Вписанный угол равен
А) дуге, на которую он опирается;
Б) удвоенной величине дуги, на которую он опирается;
В) половине дуги на которую он опирается.
4. Центральный угол равен
А) двойной величине дуги, на которую он опирается;
Б) дуге, на которую он опирается;
В) половине дуги, на которую он опирается.
5. Если две хорды окружности пересекаются, то
А) Сумма отрезков одной хорды равна сумме отрезков другой
Б) Произведение отрезков одной хорды равно произведению отрезков другой
В) хорды равны
6. Чему равен вписанный угол, опирающийся на дугу в 1200
А) 1200; Б) 600; В) 2400
7. Чему равен центральный угол, опирающийся на дугу в 400
А) 800; Б) 200; В) 400
|
8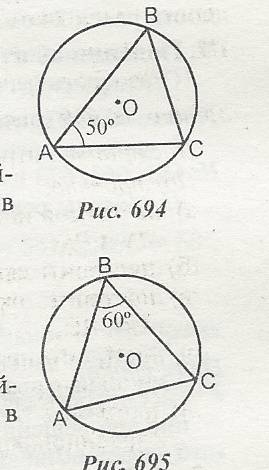 . Дано: . Дано: 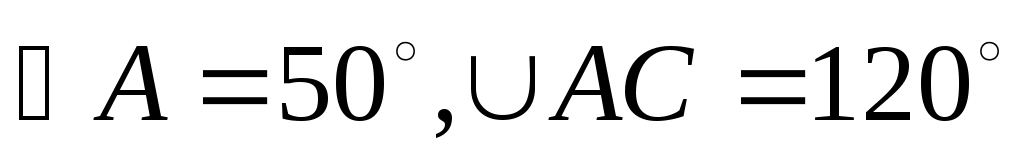
Найти: 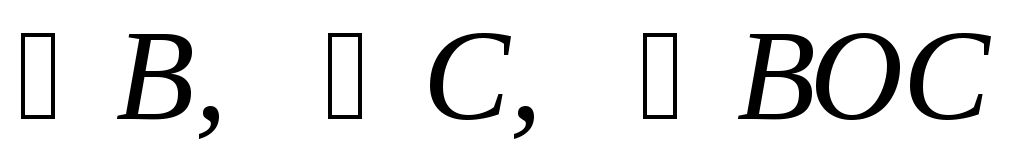
Решение.
9._Хорды MN и КР пересекаются в точке Т. Найдите MТ, если КТ = 6 см, ТР = 8 см, а NT = 12
|
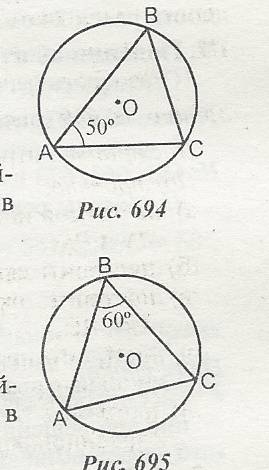 8. Дано: 8. Дано: 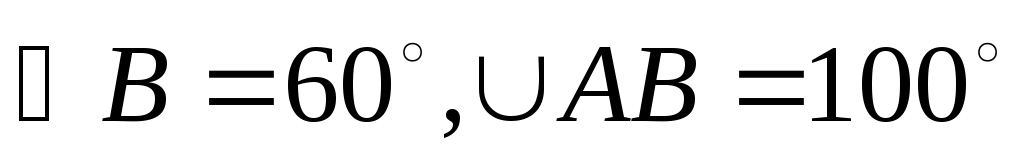
Найти: 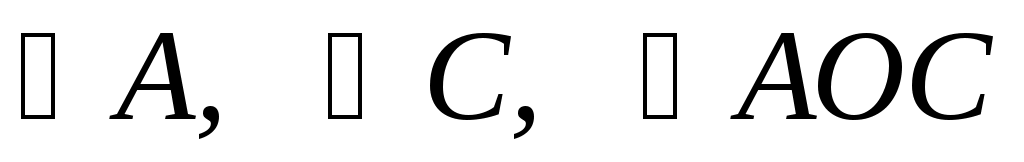
Решение.
9._ Хорды АВ и СD пересекаются в точке E. Найдите CЕ, если AE = 4 см, BE = 9 см, а DE = 6.
|
8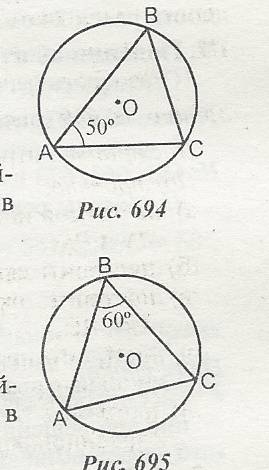 . Дано: . Дано: 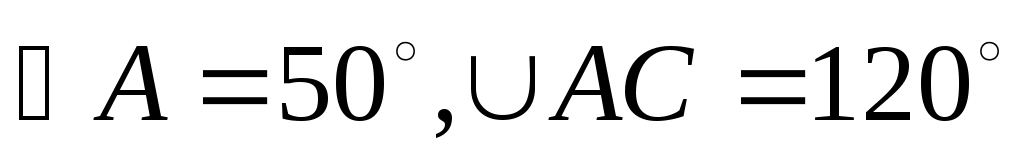
Найти: 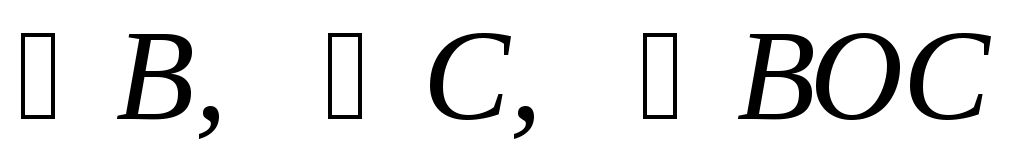
Решение.
9._Хорды MN и КР пересекаются в точке Т. Найдите MТ, если КТ = 6 см, ТР = 8 см, а NT = 12
|
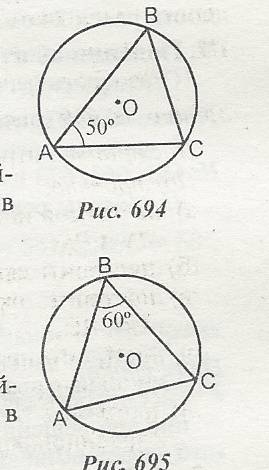 8. Дано: 8. Дано: 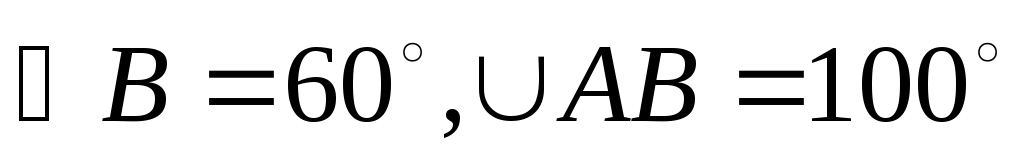
Найти: 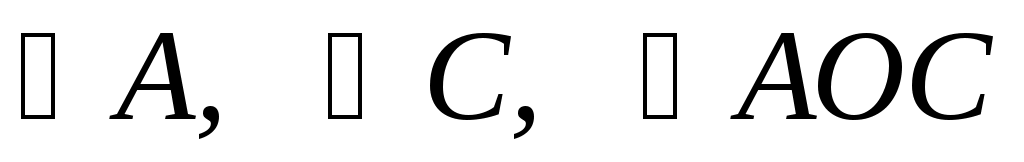
Решение.
9._ Хорды АВ и СD пересекаются в точке E. Найдите CЕ, если AE = 4 см, BE = 9 см, а DE = 6.
| |
|
|
 Скачать 97 Kb.
Скачать 97 Kb.