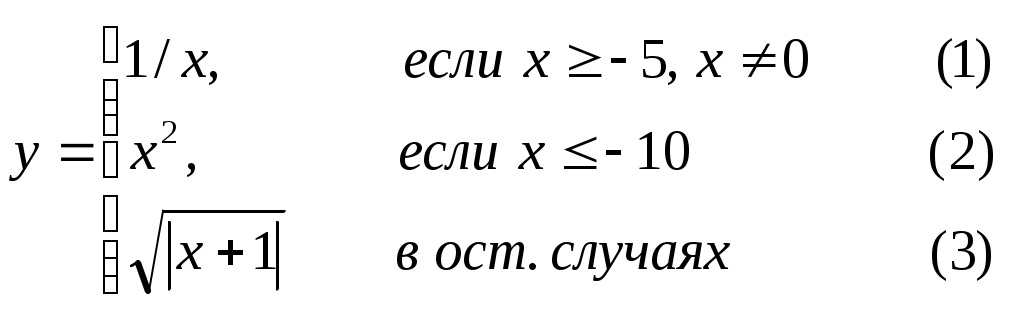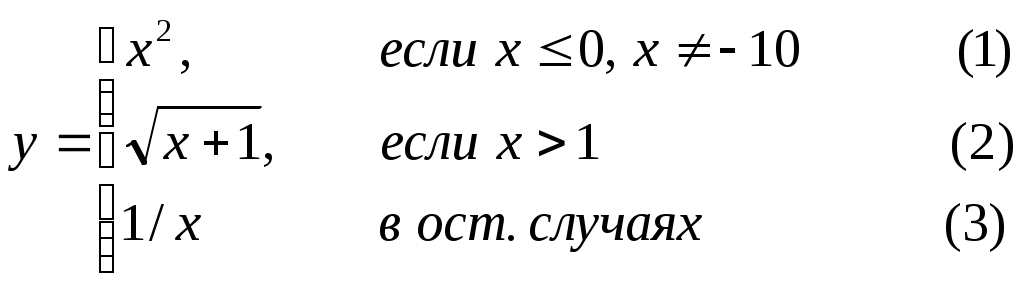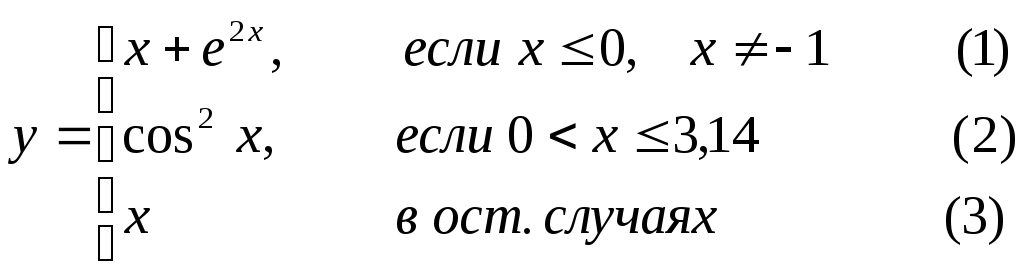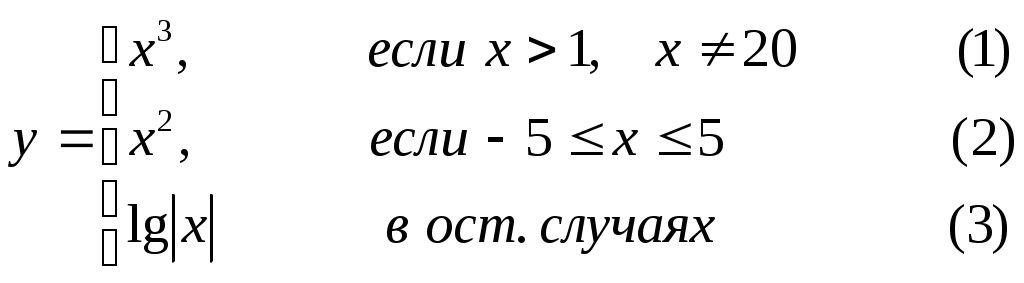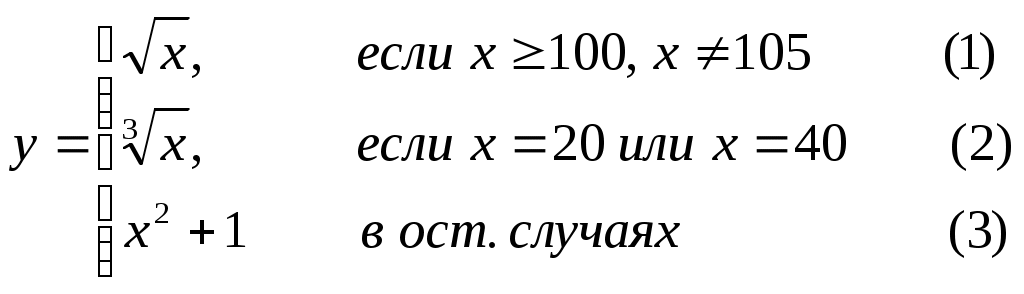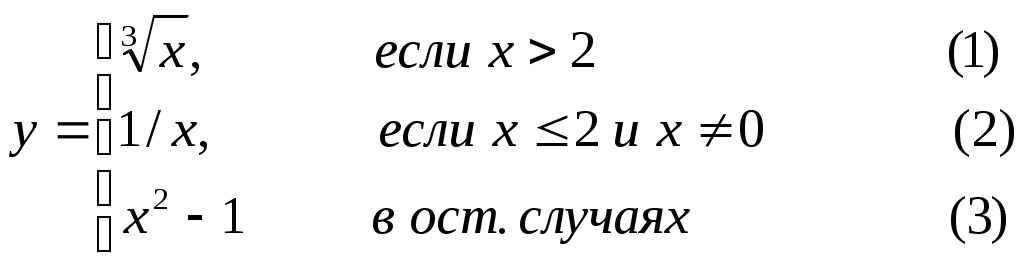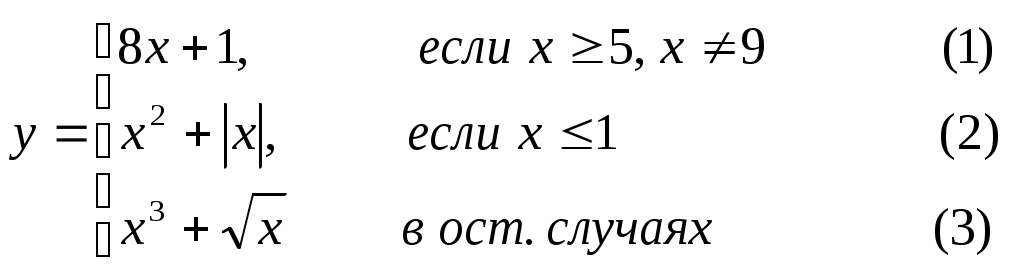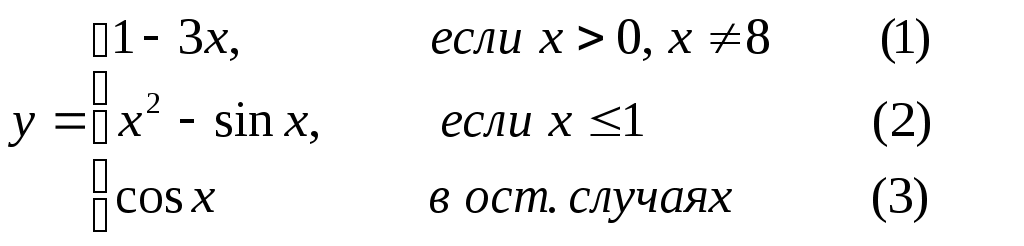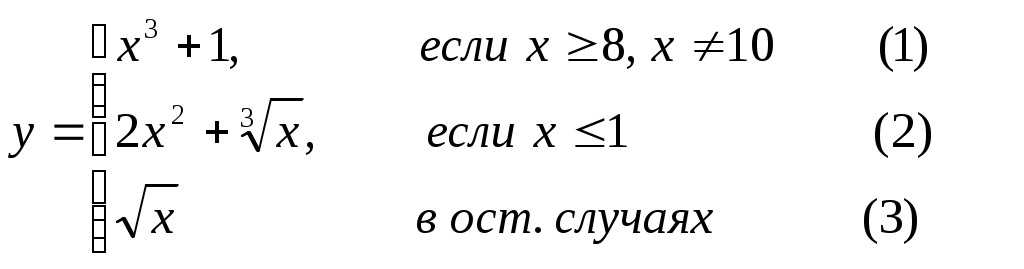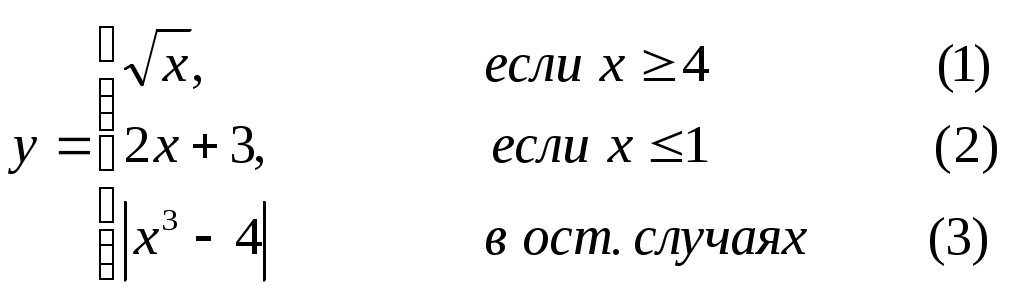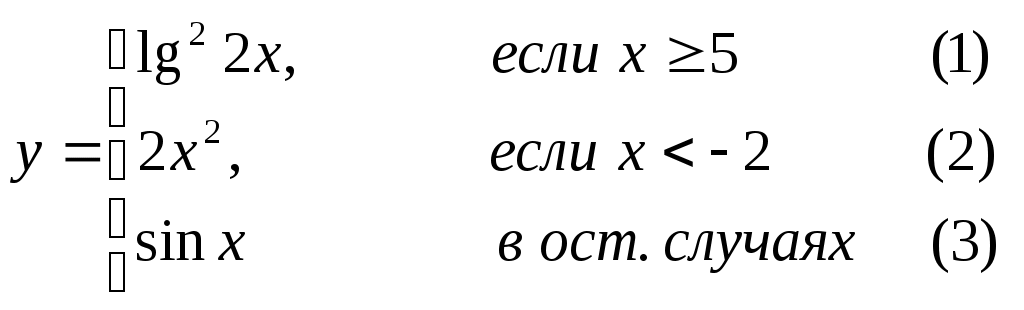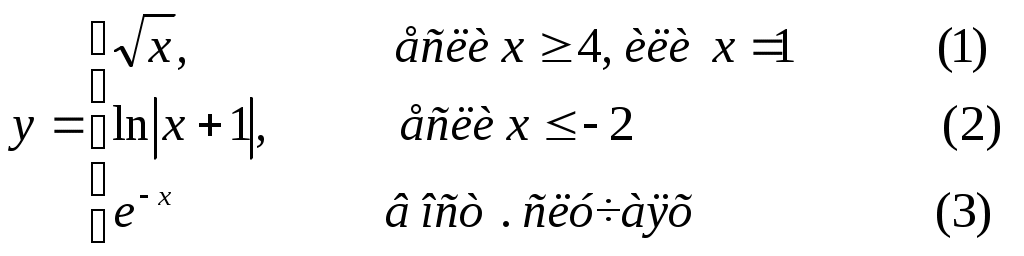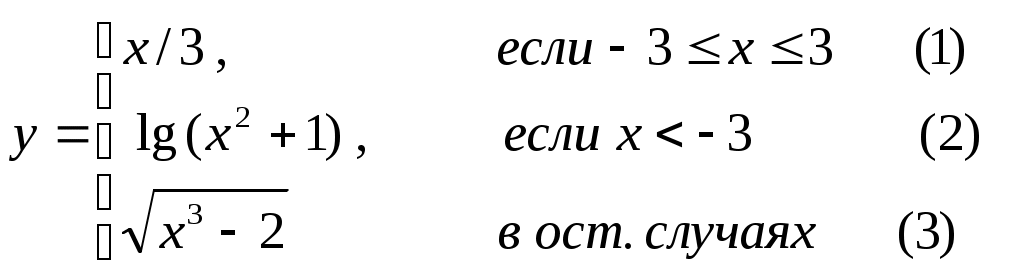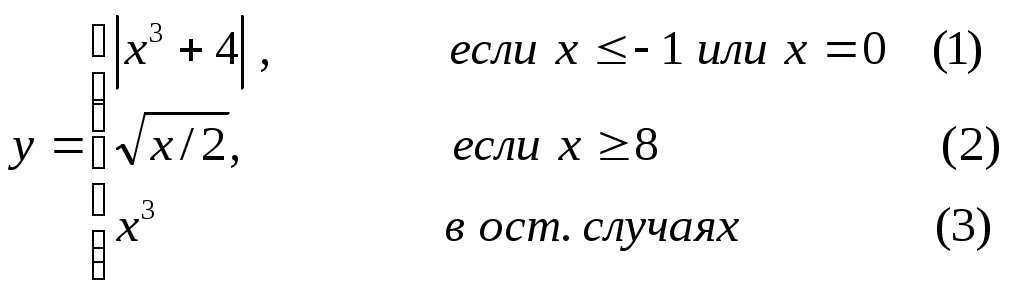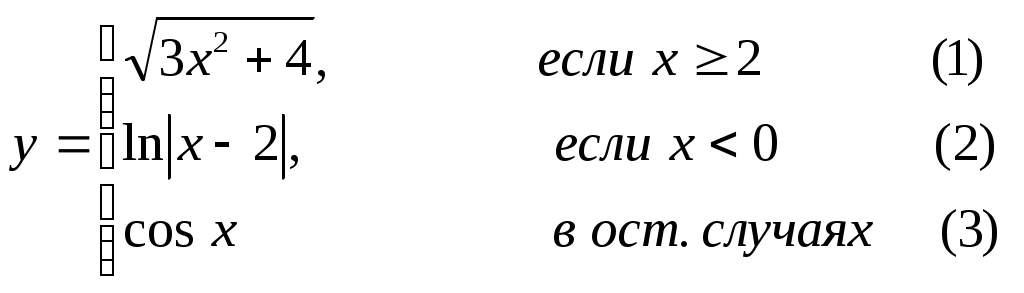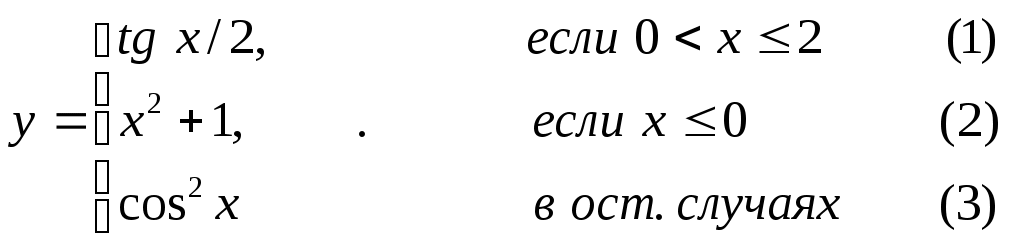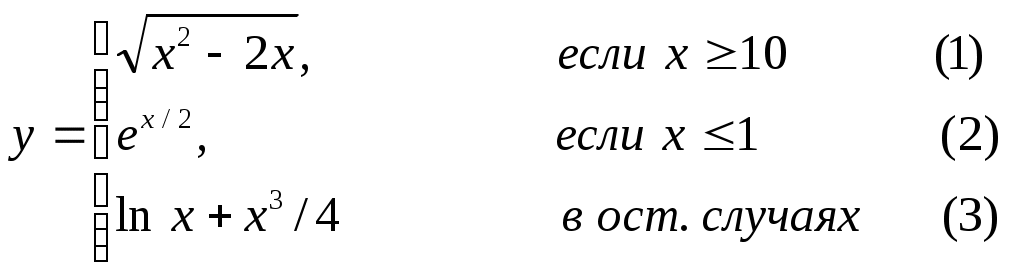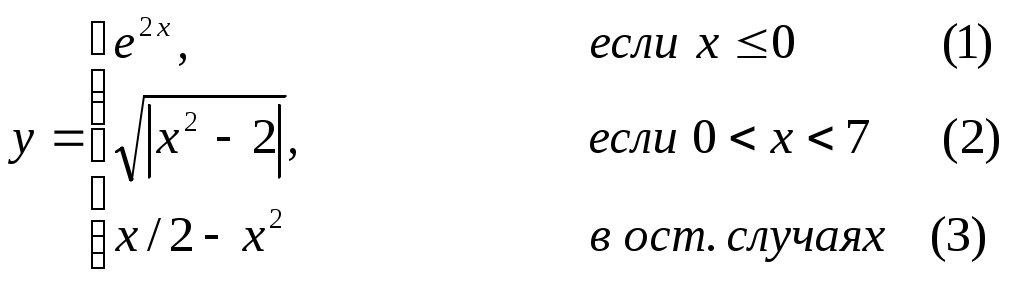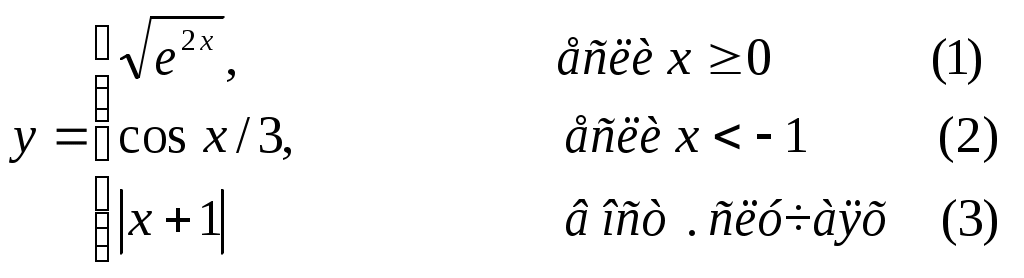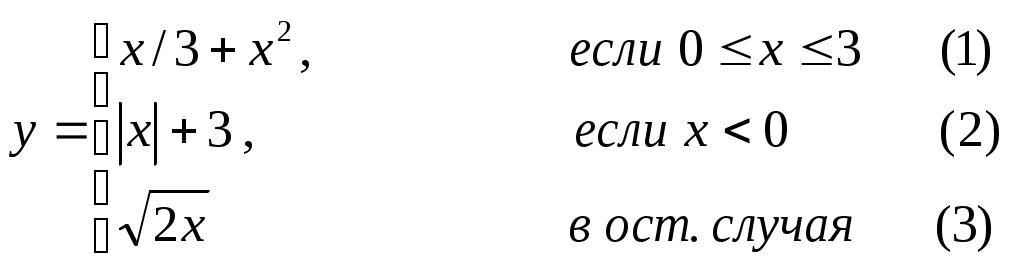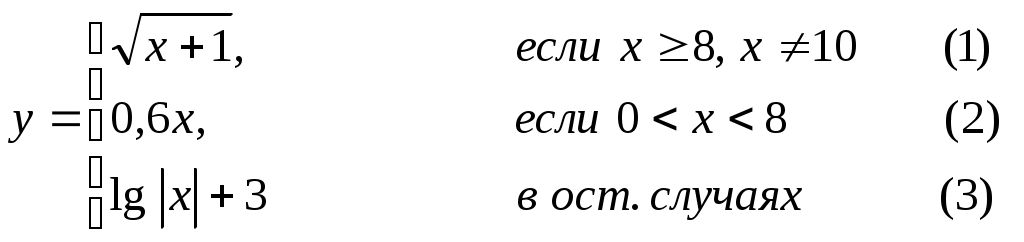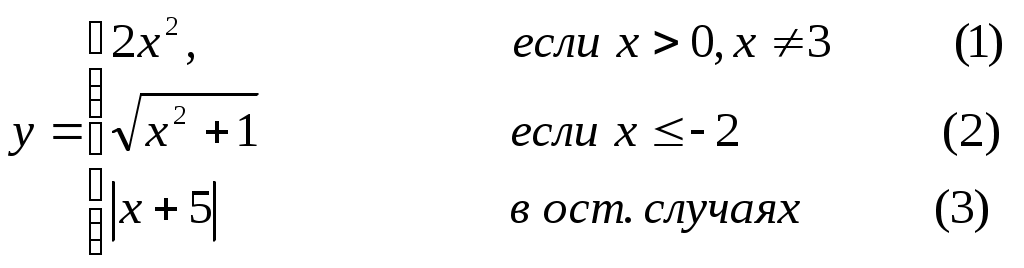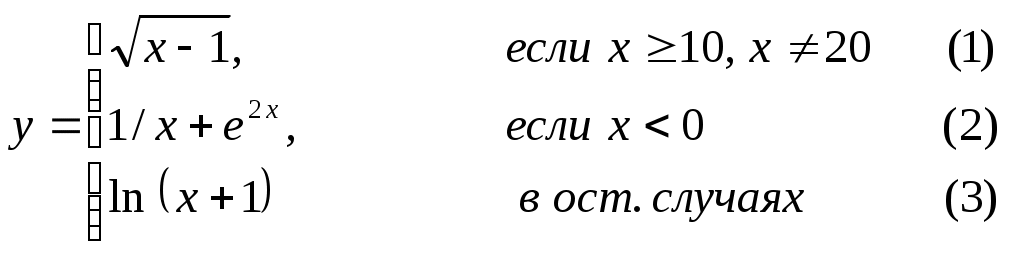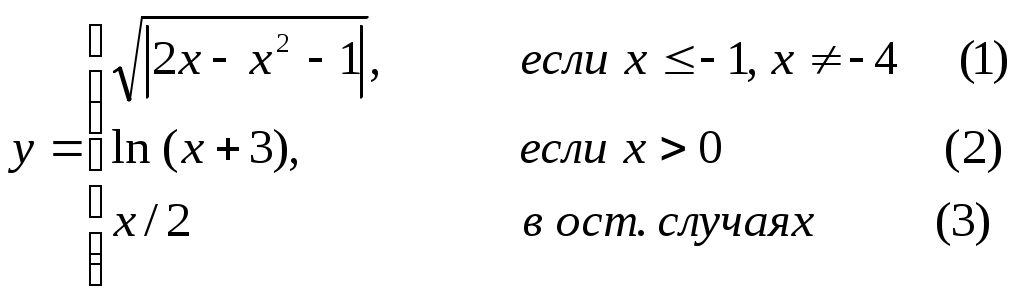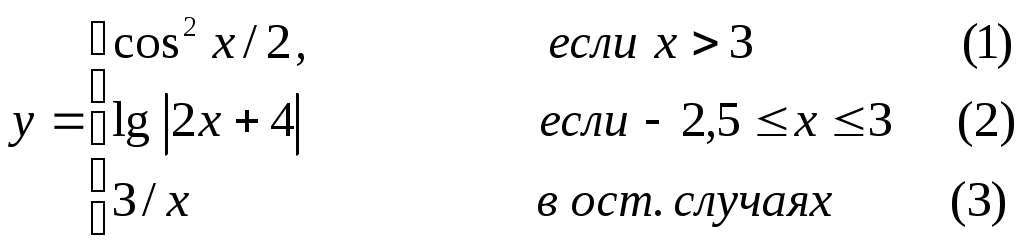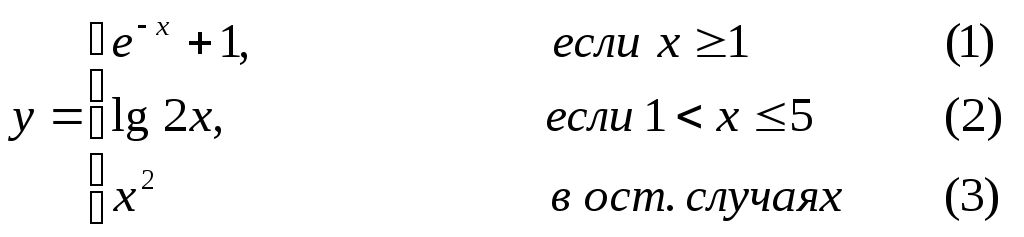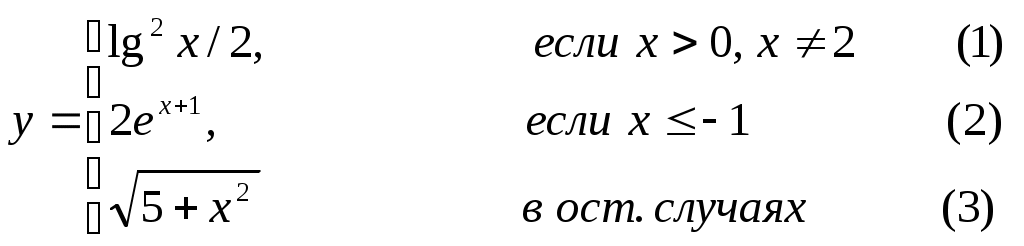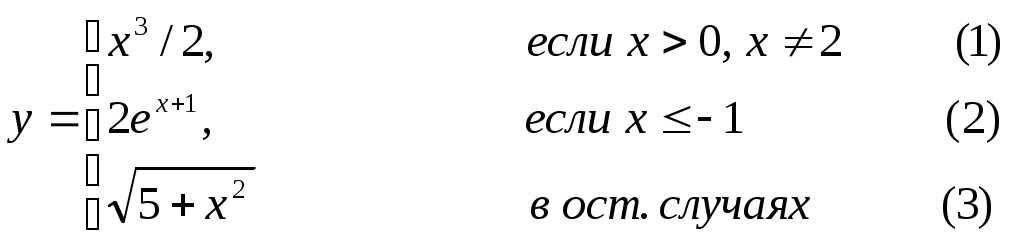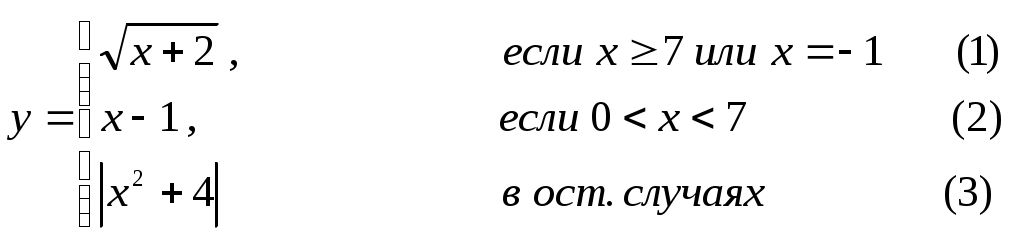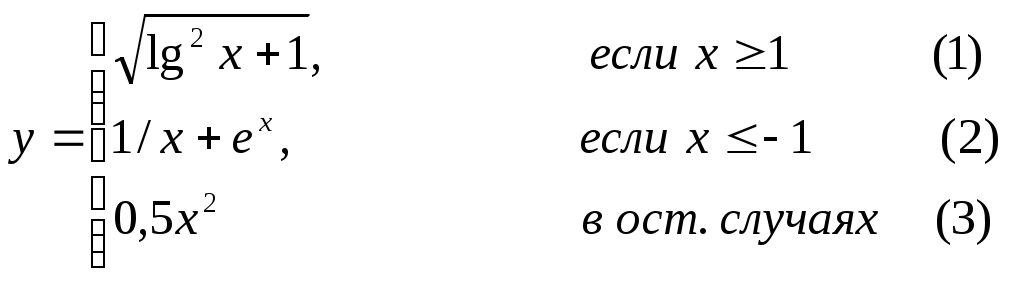Лаба12. Лабораторная работа 5. Тесты для разветвляющихся алгоритмов Для чего используется и как записывается логическое выражение
 Скачать 427 Kb. Скачать 427 Kb.
|
|
Основы конструирования программ Лабораторная работа 5 Программирование разветвляющихся алгоритмов. Цель работы: Получить навыки разработки разветвляющихся алгоритмов и их реализации. Научиться составлять тесты для проверки разветвляющейся программы. Структура отчета: Титульный лист. Цель работы. Содержание отчета для задания 1 текст задания в соответствии со своим вариантом; вид окна проекта (формы) с указанием визуальных компонентов (ВК); таблица используемых ВК; таблица используемых событий; таблица используемых переменных; схема алгоритма; рукописные тесты; распечатка текста модуля; распечатка формы с результатами работы. для задания 2: текст задания в соответствии со своим вариантом; схема алгоритма; рукописные тесты; распечатка текста модуля; распечатка формы с результатами работы Выводы. Контрольные вопросы и задания к защите: Какой алгоритм называется разветвляющимся? Как создаются тесты для разветвляющихся алгоритмов? Для чего используется и как записывается логическое выражение? Какой тип и значение имеют логические выражения? Назовите операции отношения. Для чего они используются? Назовите логические операции. От чего зависит результат выполнения логических операций? Как выполняется и как записывается условный оператор if в полной и краткой форме? Как записывается и для чего используется составной оператор? Запишите фрагмент программы, соответствующий графической схеме указанного преподавателем разветвляющегося алгоритма. Теоретические сведения к работе Разветвляющимся называется алгоритм, в котором некоторые действия (в программе операторы) могут выполняться один раз или не выполняется в зависимости от заданного условия. Условные операторыУсловный оператор if используется для разветвления процесса выполнения кода программы на два направления. В языке Си имеется две разновидности условного оператора: простой и полный. Синтаксис простого оператора: if (выражение) оператор; выражение – логическое или арифметическое выражение, вычисляемое перед проверкой, и, если выражение истинно (не равно нулю), то выполняется оператор, иначе он игнорируется; оператор – простой или составной (блок) оператор языка Си. Если в случае истинности выражения необходимо выполнить несколько операторов (более одного), их необходимо заключить в фигурные скобки. Структурная схема простого оператора приведена на рисунке 1.  Рисунок 1 – Простой оператор условного выполнения Примеры записи условного оператора if: if (x > 0) x = 0; if (i != 1) j++, s = 1; – используем операцию «запятая»; if (i != 1) { j++; s = 1; – последовательность операций (блок); } if (getch() != 27) k = 0; – если нажата любая клавиша кроме “Esc”. if (!x) exit (1); или if (x == 0) exit(1); if (i>0 && i if (a++) b++; – необязательно в качестве выражения использовать логические выражения. Синтаксис полного оператора условного выполнения: if (выражение) оператор 1 ; else оператор 2 ; Если выражение не равно нулю (истина), то выполняется оператор 1, иначе – оператор 2. Операторы 1 и 2 могут быть простыми или составными (блоками). Наличие символа «;» перед словом else в языке Си обязательно. Структурная схема такого оператора приведена на рисунке 2. 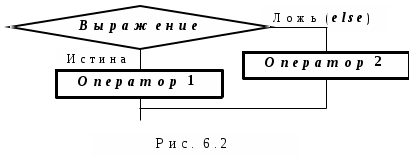 Рисунок 2 – Полный оператор условного выполнения Примеры записи: if (x > 0) j = k+10; else m = i+10; if ( x>0 && k!=0 ) { j = x/k; x += 10; } else m = k*i + 10; Операторы 1 и 2 могут быть любыми операторами, в том числе и условными. Тогда, если есть вложенная последовательность операторов if – else, то фраза else связывается с ближайшим к ней предыдущим if, не содержащим ветвь else. Например: if (n > 0) if(a > b) z = a; else z = b; Здесь ветвь else связана со вторым if (a > b). Если же необходимо связать фразу else с внешним if, то используются операторные скобки: if(n > 0) { if(a > b) z = a; } else z = b; В следующей цепочке операторов if – else – if выражения просматриваются последовательно: if (выражение 1) оператор 1; else if (выражение 2) оператор 2; else if (выражение 3) оператор 3; else оператор 4 ; Если какое-то выражение оказывается истинным, то выполняется относящийся к нему оператор и этим вся цепочка заканчивается. Каждый оператор может быть либо отдельным оператором, либо группой операторов в фигурных скобках. Оператор 4 будет выполняться только тогда, когда ни одно из проверяемых условий не подходит. Иногда при этом не нужно предпринимать никаких явных действий, тогда последний else может быть опущен или его можно использовать для контроля, чтобы зафиксировать «невозможное» условие (своеобразная экономия на проверке условий). Пример: if (x < 0) printf("\n X отрицательное \n"); else if(x==0) printf ("\n X равно нулю \n"); else printf("\n X положительное \n"); Замечание. Наиболее распространенной ошибкой при создании условных операторов является использование в выражении операции присваивания «=» вместо операции сравнения на равенство операндов «==» (два знака равно). Например, в следующем операторе синтаксической ошибки нет: if (x = 5) a++; но значение а будет увеличено на единицу независимо от значения переменной х, т.к. результатом операции присваивания х = 5 в круглых скобках является значение 50 – истина. Условная операция «? :»Условная операция – тернарная, т.к. в ней участвуют три операнда. Формат написания условной операции следующий: Выражение1?выражение2 :выражение3; если выражение 1 (условие) отлично от нуля (истинно), то результатом операции является значение выражения 2, в противном случае – значение выражения 3. Каждый раз вычисляется только одно из выражений 2 или 3. На рисунке 3 приведена схема вычисления результата, которая аналогична схеме полного оператора if (рисунок 2):  Рисунок 3 – Вычисление результата Условное вычисление применимо к арифметическим операндам и операндам-указателям. Рассмотрим участок программы для нахождения максимального значения z из двух чисел a и b, используя оператор if и условную операцию. 1. Запишем оператор if : if (a > b) z = a; else z = b; 2. Используя условную операцию, получим z = (a > b) ? a : b; Условную операцию можно использовать так же, как и любое другое выражение. Если выражения 2 и 3 имеют разные типы, то тип результата определяется по правилам преобразования. Например, если f имеет тип double, а n – int, то результатом операции (n > 0) ? f : n; по правилам преобразования типов будет double, независимо от того, положительно n или нет. Использование условных выражений позволяет во многих случаях значительно упростить программу. Например: int a, x; ... x = (a < 0) ? –a : a; printf("\n Значение %d %s нулевое !", x, (x ? "не" : " ") ); Оператор выбора альтернатив (переключатель)Оператор switch (переключатель) предназначен для разветвления процесса вычислений на несколько направлений. Общий вид оператора: switch ( выражение ) { case константа1: список операторов 1 case константа2: список операторов 2 ... case константаN: список операторов N default: список операторов N+1 – необязательная ветвь; } Выполнение оператора начинается с вычисления выражения, значение которого должно быть целого или символьного типа. Это значение сравнивается со значениями констант и используется для выбора ветви, которую нужно выполнить. В данной конструкции константы фактически выполняют роль меток. Если значение выражения совпало с одной из перечисленных констант, то управление передается в соответствующую ветвь. После этого, если выход из переключателя в данной ветви явно не указан, последовательно выполняются все остальные ветви. Все константы должны иметь разные значения, но быть одного и того же типа. Несколько меток могут следовать подряд, и тогда переход в указанную ветвь будет происходить при совпадении хотя бы одной из них. Порядок следования ветвей не регламентируется. В случае несовпадения значения выражения ни с одной из констант выбора происходит переход на метку default либо, при ее отсутствии, к оператору, следующему за оператором switch. Управляющий оператор break (разрыв) выполняет выход из оператора switch. Если по совпадению с каждой константой должна быть выполнена одна и только одна ветвь, схема оператора switch следующая: switch (выражение) { case константа1: операторы 1; break; case константа2: операторы 2; break; ... case константаN: операторы N; break; default: операторы (N+1); break; } Структурная схема рассмотренной конструкции (с использованием оператора break) приведена на рисунке 4. 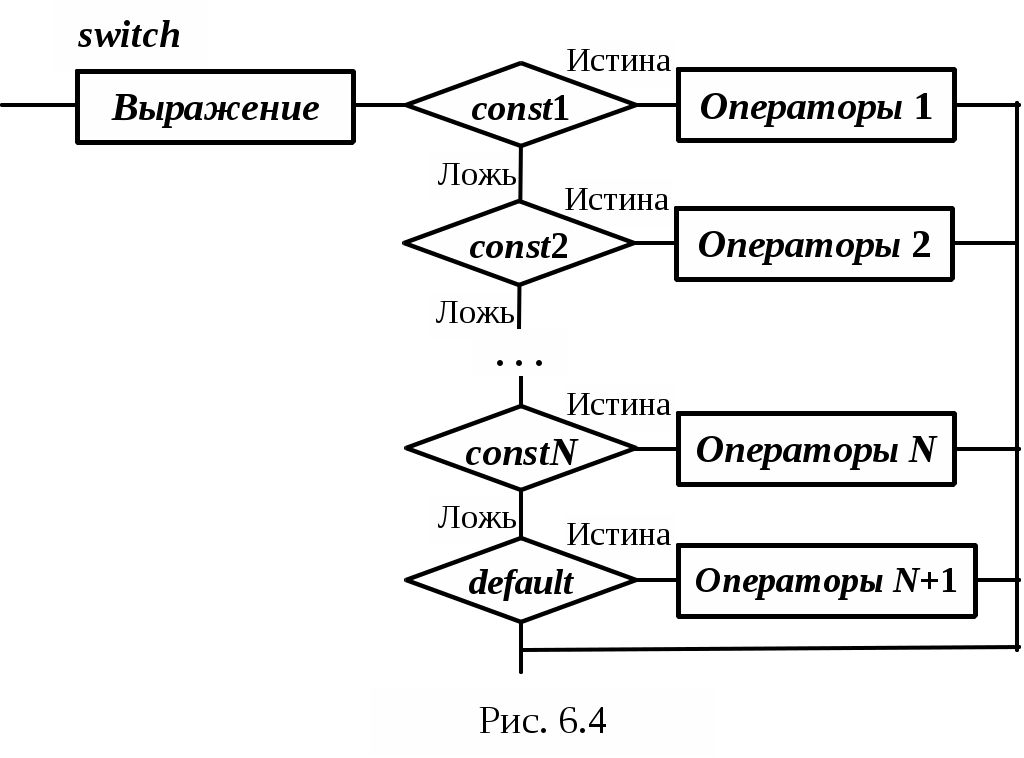 Рисунок 4 - Конструкция с использованием оператора break Пример оператора switch с использованием оператора break: void main(void) { int i = 2; switch(i) { case 1: puts ( "Случай 1. "); break; case 2: puts ( "Случай 2. "); break; case 3: puts ( "Случай 3. "); break; default: puts ( "Случай default. "); break; } } Результатом выполнения данной программы будет: Случай 2. Аналогичный пример без использования оператора break (схема общего вида такой конструкции приведена рисунок 5): void main() { int i = 2; switch(i) { case 1: puts ( "Случай 1. "); case 2: puts ( "Случай 2. "); case 3: puts ( "Случай 3. "); default: puts ( "Случай default. "); } } В данном случае результат будет следующим: Случай 2. Случай 3. Случай default. 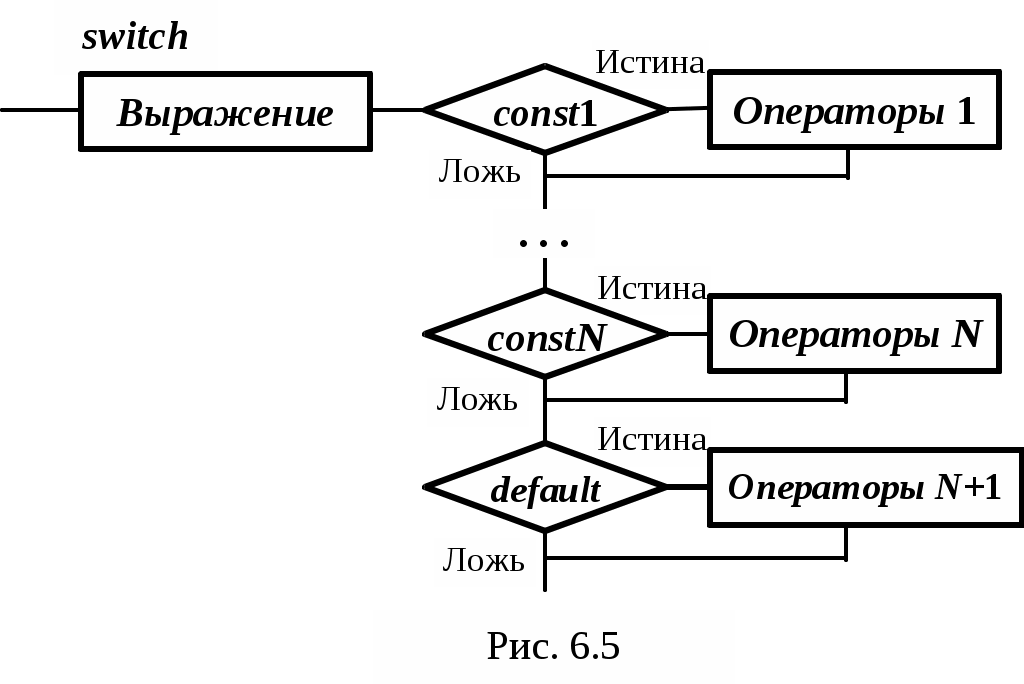 Рисунок 5 - Конструкция без использованием оператора break Пример реализации простейшего калькулятора на четыре действия с контролем правильности ввода символа нужной операции. Ввод данных осуществляется следующим образом: операнд 1, символ нужной операции, операнд 2. Текст программы может быть следующим: #include void main(void) { double a, b, c; char s; m1: fflush(stdin); // Очистка буфера ввода stdin printf("\n Введите операнд 1, символ операции, операнд 2:"); scanf("%lf%c%lf", &a, &s, &b); switch(s) { case '+': c = a+b; break; case '–': c = a–b; break; case '*': c = a*b; break; case '/': c = a/b; break; default: printf("\n Ошибка, повторите ввод! "); goto m1; } printf("\n a %c b = %lf ", s, c); printf("\n Продолжим? (Y/y) "); s = getch(); if ( (s=='Y') || (s=='y') ) goto m1; printf("\n Good bye! "); } После запуска программы на экран выводится подсказка, нужно набрать соответствующие значения без пробелов, например, как показано ниже, и нажать клавишу Enter: Введите операнд 1, символ операции, операнд 2: 2.4+3.6 На экран будет выведен результат и дальнейший диалог: a + b = 6.000000 Продолжим? (Y/y) Введя символ y (Y), вернемся в начало функции и на экране вновь появится: Введите операнд 1, символ операции, операнд 2: Если ошибочно ввести – 2r3 , появятся следующие сообщения: Ошибка, повторите ввод! Введите операнд 1, символ операции, операнд 2: 2 * 3 a*b = 6.000000 Continue? (Y/y) Нажимаем любую клавишу, кроме y или Y – следует сообщение Goodbye! Программа закончена. Рассмотрим пример разветвляющегося алгоритма с простым логическим условием. П 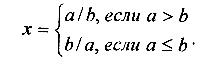 ример 1.2.Даны два числа а и b. ример 1.2.Даны два числа а и b.Найти Х Очевидно, что для определения ветви , по которому необходимо производить процесс вычисления значения х,достаточно проверить выполнение одного из условий, например а>b.Если условие а>bне выполняется, то очевидно и без дополнительной проверки, что будет выполнено условие а <b.Следовательно, вариант схемы алгоритма будет выглядеть следующим образом (рисунок 6). 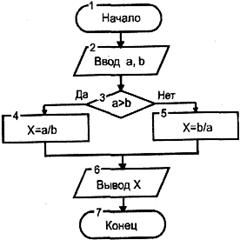 Рисунок 6 - Схема простого разветвляющегося алгоритма Рассмотрим примеры алгоритмов разветвляющейся структуры в случаях необходимости анализа более сложных логических условий. a / b, если а >0 Пример 1.3.Даны два числа а и b. Найти х = - а -b, если а = 0. а +b, если а < 0 Из условия очевидно, что предполагаемый вычислительный процесс должен предусматривать выбор одного из альтернативных путей вычислений в зависимости от значения переменной а. При этом алгоритм может быть представлен в одном из двух вариантов: с разветвлением по сложному логическому условию (рисунок 7а)и с разветвлением при разложении сложного логического условия на простые (рисунок 76). 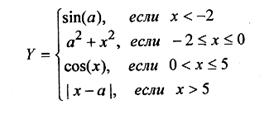 Пример 1.4.Вычислить значение Y при заданных значениях а, х. 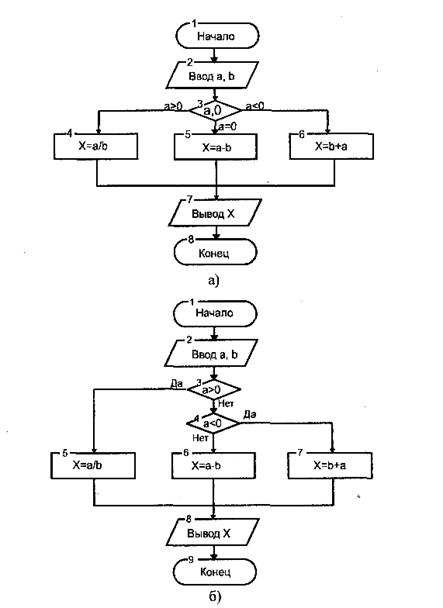 Рисунок 7 - Схемы алгоритмов разветвляющейся структуры: а) - со сложным логическим условием; б) - при разложении сложного логического условия на простые Несмотря на то что в примере предлагаются четыре логических условия, два из которых сложные, при составлении алгоритма достаточно организовать только три простых сравнения. Остальные сравнения необязательны, поскольку соответствующие условия и так являются единственно возможными при невыполнении предложенных сравнений (рисунок 8). Например, проверка логического условия х<=0(блок 5) возможна только при невыполнении условия х< -2(ветка "нет" блока 3), что в свою очередь возможнотолько при х>=-2. 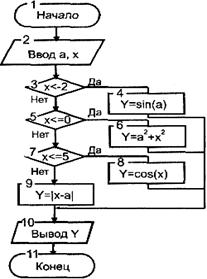 Рисунок 8 -. Схема разветвляющегося алгоритма решения примера 1.4 Пример 1.5.Даны три неравных между собой числа а,b, с.Определить наибольшее из них. В алгоритме (рисунок 9) вначале сравним между собой два первых числа аи b(блок 3). Затем большее из них сравним с оставшимся третьим числом с (блок 4 или блок 5). Большее число в этом сравнении и является наибольшим из трех. При увеличении числа переменных до 4 и более схема алгоритма потребует большого числа сравнений, что усложнит анализ условий их выполнения и может привести к ошибкам при разработке алгоритма. К тому же увеличится количество линий, соединяющих эти блоки, что усложнит читаемость алгоритма. 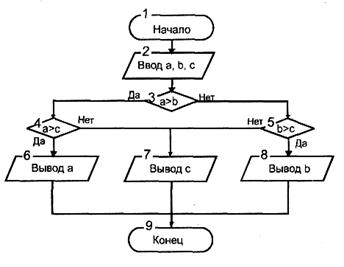 Рисунок 9 - Схема алгоритма поиска наибольшего из трех чисел Пример 1.5.Даны три неравных между собой числа а,b, с.Определить наибольшее из них. В алгоритме (рисунок 10) вначале сравним между собой два первых числа аи b(блок 3). Затем большее из них сравним с оставшимся третьим числом с (блок 4 или блок 5). Большее число в этом сравнении и является наибольшим из трех. При увеличении числа переменных до 4 и более схема алгоритма потребует большого числа сравнений, что усложнит анализ условий их выполнения и может привести к ошибкам при р 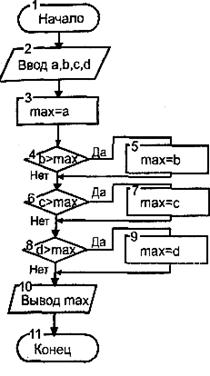 азработке алгоритма. К тому же увеличится количество линий, соединяющих эти блоки, что усложнит читаемость алгоритма. Рисунок 10 - Схема алгоритма поиска наибольшего из трех чисел Поэтому при решении подобных задач рациональнее изменить подход к нахождению максимального значения. Пример 1.6.(самостоятельно) Заданы четыре неравные между собой величины а,b, с,d. Определить наибольшую из них. Пример 1.7.(самостоятельно)Даны три неравных между собой числа а,b, с.Вывести эти числа на печать в порядке убывания их значений. Задания к работе Задание 1. Разработать интерфейс проекта, составить графическую схему алгоритма и программу вычисления функции y=f(x) в соответствии с видом функции, приведенном в таблице.1. Для ввода исходных данных, вывода исходных данных и результатов использовать только одну форму. В программе предусмотреть вывод результатов для всех тестов: значения аргумента функции x; вычисленного значения функции y; номера формулы, по которой производилось вычисление функции (1, 2 или 3). Исходные данные для отладки программы выбрать самостоятельно. Выполнить тестирование программы для каждого интервала изменения функции и для каждой точки ветвления функции. Таблица 1
Задание 2. Выполнить задание в соответствии со своим вариантом в таблице 2. Для ввода исходных данных, вывода исходных данных и результатов использовать только одну форму. Вывести условие задачи в многострочном текстовом поле, исключив возможность его изменения на этапе выполнения. Исходные данные для отладки программы выбрать самостоятельно так, чтобы проверить все возможные варианты выполнения программы. Таблица 2
|