непараметрические тесты для независимых выборок. Тесты для сравнения двух независимых выборок. Uкритерий МаннаУитни Курдюкова Е. В. Сафу, вшитас

• Название: Тесты для сравнения двух независимых выборок. Uкритерий МаннаУитни Курдюкова Е. В. Сафу, вшитас
• Дата: 18.05.2018
• Размер: 0.86 Mb.
• Имя файла: непараметрические тесты для независимых выборок.docx
• Тип: Тесты; #44107

Непараметрические тесты для сравнения двух независимых выборок. U-критерий Манна-Уитни

Курдюкова Е.В. САФУ, ВШИТАС

U-критерий Манна-Уитни – непараметрический статистический критерий, используемый для сравнения двух независимых выборок по уровню какого-либо признака. Метод основан на определении того, достаточно ли мала зона перекрещивающихся значений между двумя вариационными рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке).

U-критерий Манна-Уитни является непараметрическим критерием, поэтому, в отличие от t-критерия Стьюдента, не требует наличия нормального распределения сравниваемых совокупностей.

U-критерий подходит для сравнения малых выборок: в каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было 2 значения, но во второй тогда должно быть не менее пяти.

Условием для применения U-критерия Манна-Уитни является отсутствие в сравниваемых группах совпадающих значений признака (все числа – разные) или очень малое число таких совпадений.

U-критерий Манна-Уитни подсчитывается по формуле:

U_эмп = n₁ * n₂ + (n_x * (n_x +1)/2) - t_{x ,} где n₁ и n₂ – это объемы выборок, n_x – объем выборок с наибольшей ранговой суммой t_x

Задача 1.

Студенты физического и психологического факультетов Ленинградского университета были обследованы с помощью методики Д. Векслера для измерения вербального и невербального интеллекта. Показатели невербального интеллекта сформированы в таблицу 2. Можно ли утверждать, что одна из выборок превосходит другую по уровню невербального интеллекта?

№ испытуемых	Студенты-физики	Студенты-психологи
1	111	113
2	104	107
3	107	123
4	90	122
5	115	117
6	107	112
7	106	105
8	107	108
9	95	111
10	116	114
11	127	102
12	115	104

Решение.

Выдвигаем гипотезы:

H₀ – выборки значимо не различаются по уровню невербального интеллекта

H₁ – выборки значимо различаются по уровню невербального интеллекта

Распределим данные таблицы по рангам, также подсчитаем сумму рангов по каждой выборке.

№ испытуемых	Студенты-физики	Ранг	Студенты-психологи	Ранг
1	111	13,5	113	16
2	104	4,5 ((4+5)/2)	107	9,5
3	107	9,5	123	23
4	90	1	122	22
5	115	18,5	117	21
6	107	9,5	112	15
7	106	7	105	6
8	107	9,5	108	12
9	95	2	111	13,5
10	116	20	114	17
11	127	24	102	3
12	115	18,5	104	4,5
		t1 =137,5		t2 =162,5

t₂ > t_1, следовательно для подсчета мы будем использовать t₂.

U_эмп = 12 * 12 + (12 * (12 +1) /2) – 162,5 = 144 + 78 – 162,5 = 222 – 162,5 = 59,5

Обратимся к таблице критических значений критерия Манна Уитни. В нашем случае (n₁ = 12 и n₂ = 12) U_крит = 37.

U_эмп > U_крит, следовательно мы принимаем гипотезу h₀. Выборки значимо не различаются по уровню невербального интеллекта. Следовательно, мы не можем утверждать, что одна из выборок превосходит другую по уровню невербального интеллекта.

Теперь решим задачу при помощи программы IBM SPSS.

1. 
   Вносим в программу переменные «№», «Невербальный интеллект» и «Студенты» (рисунок 1).
   

Рисунок 1 – Переменные

В графе «Значения» для переменной «Студенты» проставим метки и соответствующие им значения. В нашем случае значению 1 соответствуют «физики», а значению 2 – «психологи» (рисунок 2).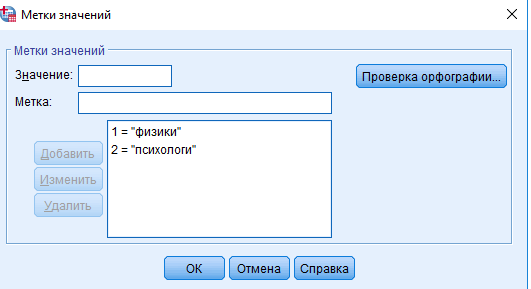


Рисунок 2 – Метки значений

2. 
   Вносим во вкладке «Данные» показатели невербального интеллекта для переменной «Невербальный интеллект». Обе выборки располагаем в одном столбце, так как при проведении непараметрических тестов в SPSS выборки формируются автоматически через группирующую переменную.
   

В столбце переменной «Студенты» распределяем выборки по группам (физики или психологи): 1 или 2.



Рисунок 3 – Данные

3. 
   Выбираем путь: Анализ – Непараметрические критерии – Устаревшие диалоговые окна – Для двух независимых выборок (рисунок 4).
   

Рисунок 4 – Путь в программе

В «Список проверяемых переменных» вносим переменную «Невербальный интеллект», переменную «Студенты» перетягиваем в поле «Группировать по» (рисунок 5). Оставляем галочку рядом с критерием Манна-Уитни.



Рисунок 5 – Критерии для двух независимых выборок

Задаем группы (рисунок 6).


Рисунок 6 – Задать группы

4. 
   Нажимаем на кнопку ОК. Перед нами появляется окно выводов (рисунок 7). В таблице «Ранги» мы видим информацию по каждой выборке, в том числе, сумму рангов. В таблице «Статистические критерии» обозначен U критерий Манна Уитни, который равен 59,500. Асимптоническое значение равно 0,469.
   

0,469 > α0,05, следовательно мы принимаем гипотезу h₀ - – выборки значимо не различаются по уровню невербального интеллекта.



Рисунок 7 – Выводы

Задача 2.

Утомленная изучением статистики студентка Катя посетила несколько магазинов, чтобы определить, действительно ли цены на простоквашу значительно различаются в зависимости от сорта. Ее наблюдения приводятся ниже. Может ли Катя сделать вывод, что цены на простоквашу зависят от сорта?

Цена в условных единицах
Сорт A	Сорт B	Сорт C	Сорт D
61	52	47	67
55	58	52	63
57	54	49	68
60	55	49	69

Решение.

Гипотеза h₀ – сорт простокваши значимо не влияет на ее цену.

Гипотеза h₁ – сорт простокваши влияет на цену.

В задаче 4 независимых выборки, поэтому используем H-тест Крускала-Уоллиса. Этот тест является модификацией U-теста Манна и Уитни на случай для более двух независимых выборок. Он также базируется на общей ранговой последовательности значений всех выборок.

Воспользуемся программой IBM SPSS.

1. 
   Вносим переменные «№», «Цена», «Сорт» (рисунок 8).
   

Рисунок 8 - Переменные
В графе «Значения» для переменной «Сорт» проставим метки и соответствующие им значения (рисунок 9). В нашем случае значению 1 соответствуют «Сорт А», а значению 2 – «Сорт B», 3 - «Сорт C», 4 – «Coрт D».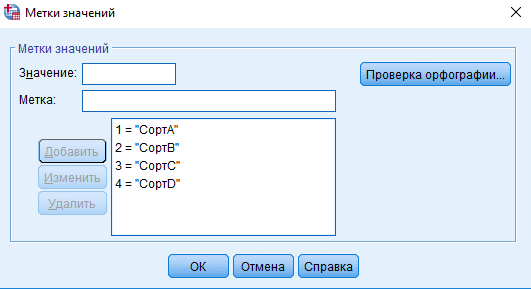


Рисунок 9 – Метки значений

2. 
   Вносим данные (рисунок 10). Все выборки располагаем в одном столбце, так как при проведении непараметрических тестов в SPSS выборки формируются автоматически через группирующую переменную. В графе «Сорт» указываем значение, соответствующее сорту: 1, 2, 3 или 4.
   

Рисунок 10 – Данные

3. 
   Выбираем путь: Анализ – Непараметрические критерии – Устаревшие диалоговые окна – Для K независимых выборок (рисунок 11).
   

Рисунок 11 – Путь в программе
В диалоговом окне «Критерии для нескольких независимых выборок» в «Список проверяемых переменных» вносим переменную «Цена». Группирующей переменной будет «Сорт» (рисунок 12).



Рисунок 12 – Критерии для нескольких независимых выборок
Так как у нас четыре независимых выборки, то правильно указываем диапазон для группирующей переменной: от 1 до 4 (рисунок 13).


Рисунок 13 – Диапазон

4. 
   После нажатия кнопки «ОК» появляется окно выводов.
   

Рисунок 14 – Окно выводов
Так как наше исследование проводится для 4 групп, а не для 3, мы используем не специальную таблицу для теста Крускала-Уоллиса, а таблицу для определения критических значений критерия Χ² .Учитываем, что количество степеней свободы в нашем случае равно 3. При p ≤ 0,01 Χ²_кр = 11,345, при p ≤ 0,05 Χ² _кр = 7,815.

Согласно окну выводов, H_эмп = 13,233. H_эмп ≥ Χ²_кр, следовательно мы принимаем гипотезу h₁ – сорт простокваши влияет на цену.
5. Так как мы отклонили гипотезу h₀, то должны провести апостериорные попарные сравнения. Для этого воспользуемся U-критерием Манна-Уитни. Выбираем путь: Анализ – Непараметрические критерии – Устаревшие диалоговые окна – Для двух независимых выборок. В диалоговом окне «Критерии для двух независимых выборок» задаем проверяемую переменную («Цена») и группирующую переменную («Сорт»). В первом случае мы будем сравнивать простоквашу сортов A и B, поэтому правильно задаем группы: в графе «Группа 1» ставим 1, а в графе «Группа 2» – 2.



Рисунок 15 – Критерии для двух независимых выборок

6. 
   В окне выводов мы видим, что P = 0,110 (рисунок 16).
   

Рисунок 16 – Сорт А и B

7. Аналогично сравниваем другие сорта простокваши.

Для сортов B и С в окне выводов мы видим, что P = 0,028 (рисунок 17).



Рисунок 17 – Сорта B и С
Для сортов C и D в окне выводов мы видим, что P = 0,020 (рисунок 18).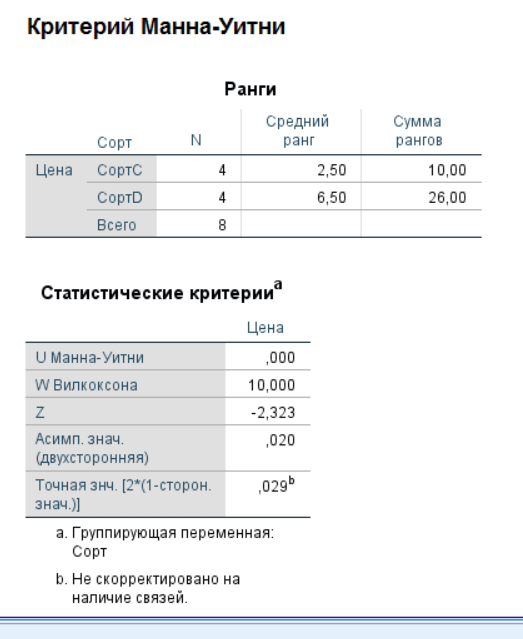



Рисунок 18 – C и D
Для сортов A и C P = 0,020 (рисунок 19).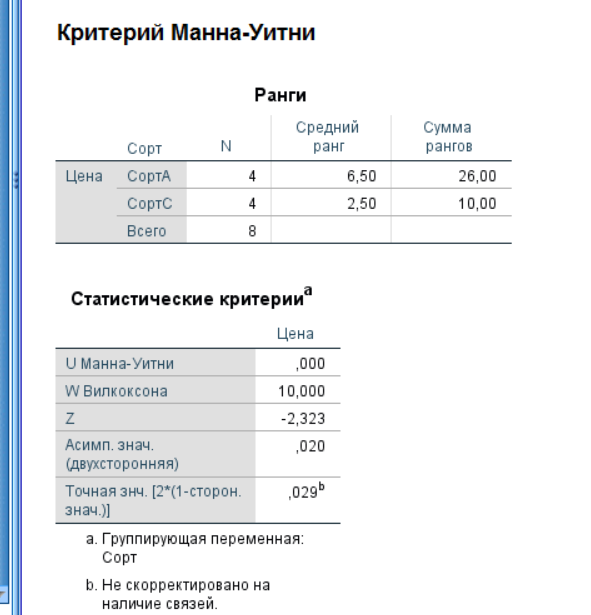



Рисунок 19 – A и С
Для сортов A и D P = 0,021 (рисунок 20).



Рисунок 20 – A и D
Для сортов B и D P = 0,021 (рисунок 21).


Рисунок 21 – В и D
Таким образом, цены значимо не различаются только в случае сортов A и B, так как P > α0,05. В остальных случаях гипотеза h₀ отвергается и цены значимо различаются (P < α0,05).

U-критерий Манна-Уитни очень удобен для сравнения двух независимых выборок по уровню какого-либо признака. Для большего количества используется H-тест Крускала-Уоллиса.