векторы тесты 11 класс. Тесты по геометрии для 11 класса 2013 г. В данной работе представлены тесты по двум разделам Радел 1 включает тему Векторы в пространстве. Метод координат в пространстве
 Скачать 0.54 Mb.
|
|
Уровень А 1. Какое утверждение неверное? 1) Любые два противоположно направленных вектора коллинеарны. 2) Любые два коллинеарных вектора сонаправлены. 3) Любые два равных вектора коллинеарны. 2. Даны точки А, В, С, D, K. Известно, что    Тогда неверно, что… 1) все точки лежат в одной плоскости; 2) прямые ВС и DK параллельны; 3) точки А, С и D не лежат на одной прямой. 3. Какое утверждение неверное? 1) Длины противоположных векторов не могут быть неравны. 2) Если длины векторов неравны, то и векторы неравны. 3) Если длины векторов равны, то и векторы равны. 4.  причём точки А, В и С не лежат на одной прямой. Прямые АС и BD не могут быть…1) параллельными; 2) пересекающимися; 3) скрещивающимися. 5. ABCA1B1C1 – правильная призма. A1F = FB1, B1K = KC1. Какое утверждение неверное? 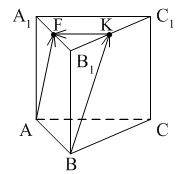 1)  2)  3)  6. ABCA1B1C1 – правильная призма. CE = EC1, BF = FB1, FM = MB1, AD : DC = 3 : 1. Какое утверждение верное? 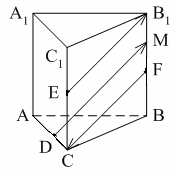 1)  2)  3)  7. ABCDA1B1C1D1 – параллелепипед. 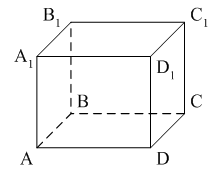 … 1)  2)  3)  8. Векторы  и  являются…1) равными; 2) противоположными; 3) сонаправленными. 9. DABC – тетраэдр.  Тогда 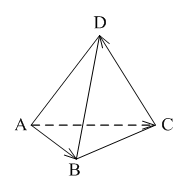 … 1)  2)  3)  Уровень В 1. ABCDA1B1C1D1 – параллелепипед. Тогда  …тест по теме: «Векторы в пространстве. Сложение и вычитание векторов. Умножение вектора на число» Вариант №2 Уровень А 1. Какое утверждение верное? 1) Любые два сонаправленных вектора коллинеарны. 2) Любые два коллинеарных вектора противоположно направлены. 3) Любые два коллинеарных вектора равны. 2. Какое утверждение верное? 1) Если   то  2) Если  то 3) Существуют векторы   и  такие, что  и не коллинеарны, и не коллинеарны, а и коллинеарны.3. Какое утверждение неверное? 1) Если длины векторов равны, то и векторы равны. 2) Если векторы равны, то их длины равны. 3) Длины противоположных векторов равны. 4.  причём точки А, В и С не лежат на одной прямой. Прямые АС и BD являются параллельными, если…1) k = 1; 2) k = –1; 3) k = 3. 5. ABCA1B1C1 – правильная призма. A1F = FB1, B1E = EC1. Какое утверждение неверное? 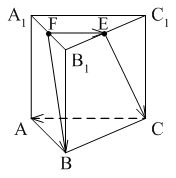 1)  2)  3)  6. FABCD – правильная пирамида. 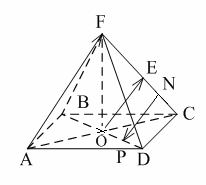 FE = EC, EN = NC, OP = PD. Какое утверждение верное? 1)  2)  3)  7. ABCA1B1C1 – призма. 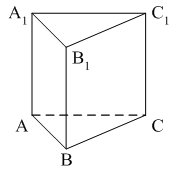 … 1)  2)  3)  8. Векторы –  и  являются…1) противоположными; 2) равными; 3) сонаправленными. 9. DABC – тетраэдр. 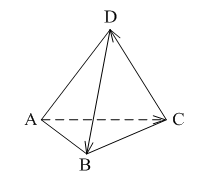 … 1)  2)  3)  Уровень В 1. ABCDA1B1C1D1 – параллелепипед. Тогда  Тест по теме: «Координаты точки и координаты вектора» Вариант №1 Уровень А 1. Точка M (–2; 3; –7) находится от плоскости XOY на расстоянии, равном… 1) 7; 2) 2; 3) 3. 2.  Тогда вектор  имеет координаты…1)  2)  3)  3.    Тогда коллинеарными будут векторы…1) и  2) и  3) и  4. Первая и третья координаты ненулевого вектора равны нулю. Тогда неверно, что…1)  2)  3)  5. Первая координата ненулевого вектора  равна нулю. Тогда неверно, что…1)  2)  3)  6. А (1; 2; 3), В (1; 5; 4), С (4; 5; 3). Тогда верно, что… 1)  2)  3)  7. Ордината точки А равна 3, ордината точки В равна 6. Длина отрезка АВ равна 3. Тогда прямая АВ и ось OY… 1) параллельны; 2) перпендикулярны; 3) скрещиваются. 8. M (x1; y1; z1), K (x2; y2; z2). Тогда координаты вектора  равны…1)  2)  3)  9.  Тогда верно, что…1)  2)  3)  Уровень В 1. Дана точка А (–1; 2; 5). Тогда координаты точки – проекции точки А на ось OZ равны… 2. Даны точки M (–1; 2; 3) и В (1; –1; 5). Тогда координаты вектора  равны…3. А (–1; 0; 2), В (1; –2; 3). Тогда  …4. ABCD – параллелограмм,  В (–2; 1; 0), О (0; 1,5; 0). Тогда координаты точки D равны…5. Вектор сонаправлен с вектором   Тогда координаты вектора равны…Тест по теме: «Координаты точки и координаты вектора» Вариант №2 Уровень А 1. Точка А (–1; 2; –3) находится от плоскости YOZ на расстоянии, равном… 1) 1; 2) 2; 3) 3. 2.  Тогда вектор имеет координаты…1)  2)  3)  3. Координаты равных векторов… 1) равны; 2) противоположны; 1) пропорциональны. 4. Первая и вторая координаты ненулевого вектора равны нулю. Тогда верно, что…1)  2) 3)  5. Третья координата ненулевого вектора равна нулю. Тогда неверно, что…1)  2)  3)  6. А (2; 3; 4), В (2; 5; 6), С (5; 3; 6). Тогда верно, что… 1)  2)  3)  7. Абсцисса точки А равна 3, абсцисса точки В равна 6. Длина отрезка АВ равна 3. Тогда прямая АВ и ось OX… 1) параллельны; 2) пересекаются; 3) скрещиваются. 8. M (x1; y1; z1), K (x2; y2; z2). Тогда длина вектора  равна…1)  2)  3)  9. A (x1; y1; z1), B (x2; y2; z2). Тогда координаты точки – середины отрезка АВ равны… 1)  2)  3)  Уровень В 1. Дана точка А (–1; 2; 5). Тогда координаты точки – проекции точки А на плоскость OYZ равны… 2. Даны точки K (2; –1; –3) и M (1; –2; 3). Тогда координаты вектора равны…3. А (7; 1; –5), В (4; –3; –5). Тогда …4. В параллелограмме ABCD диагонали пересекаются в точке О. А (1; 3; –1), О (0; 1,5; 0). Тогда координаты точки С равны… 5. Вектор противоположно направлен вектору   Тогда координаты вектора  равны…тест по теме: «Компланарные векторы» Вариант №1 Уровень А 1. Какое утверждение верное? 1) Любые два вектора компланарны. 2) Любые три вектора компланарны. 3) Три нулевых вектора компланарны. 2. Какое утверждение верное? 1) Если один из трёх векторов нулевой, то векторы компланарны. 2) Если векторы компланарны, то один из них нулевой. 3) Если векторы компланарны, то они равны. 3. ABCDA1B1C1D1 – параллелепипед. Являются компланарными векторы… 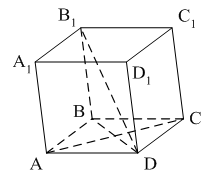 1)  2)  3)  4. Известно, что  Тогда векторы  и  являются…1) коллинеарными; 2) компланарными; 3) некомпланарными. 5. Векторы  и некомпланарны, если…1)  2)  3)  6. DABC – тетраэдр. О – точка пересечения медиан грани ABD. Тогда 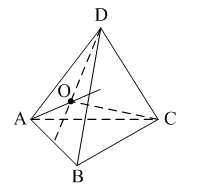 … 1)  2)  3)  7. Диагонали параллелограмма ABCD пересекаются в точке M. Точка О – произвольная точка пространства. 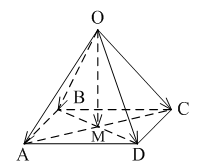 Тогда k = … 1) 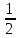 2) 2 3)  8. Какое утверждение неверное? 1) Коллинеарные векторы компланарны. 2) Если векторы компланарны, то они коллинеарны. 3) Векторы компланарны, если имеются равные им векторы, лежащие в одной плоскости. Уровень В 1. Векторы   …2. Точки А, В и С лежат на окружности, а точка О не лежит в плоскости этой окружности. Тогда векторы  и  …3. ABCDA1B1C1D1 – прямой параллелепипед,  см. ABCD – квадрат, АВ = 2 см. Тогда  …тест по теме: «Компланарные векторы» Вариант №2 Уровень А 1. Какое утверждение верное? 1) Любые два вектора не могут не быть компланарными. 2) Любые три вектора некомпланарны. 3) Только нулевые три вектора компланарны. 2. Какое утверждение неверное? 1) Три вектора компланарны, если любые два из них коллинеарны. 2) Если векторы компланарны, то любые два из них коллинеарны. 3) Любые три равных вектора компланарны. 3. FABCD – пирамида. ABCD – параллелограмм. Не являются компланарными векторы… 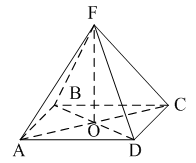 1)  2)  3)  4.  Тогда прямые АС и BD…1) пересекаются; 2) скрещиваются; 3) параллельные. 5. Векторы и некомпланарны, если…1)  2)  3)  6. DABC – тетраэдр. О – точка пересечения медиан грани BDC. Тогда 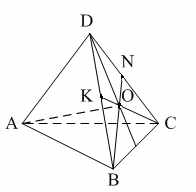 … 1)  2)  3)  7. Точки M, N, P, K – середины сторон четырёхугольника ABCD.  Точка 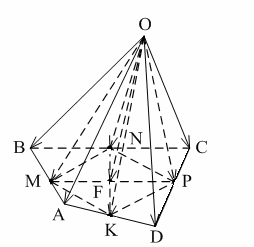О – произвольная точка пространства. Тогда  … 1)  2)  3)  8. Какое утверждение неверное? 1) Прямые, содержащие компланарные векторы, лежат в одной плоскости. 2) Если векторы лежат в одной плоскости, то они компланарны. 3) Если вектор можно разложить по векторам и , то векторы и компланарны.Уровень В 1. Известно, что векторы и компланарны. Тогда векторы    …2. Точки А, В и С не лежат на одной прямой, а точка О не лежит в плоскости (АВС). Тогда векторы и …3. ABCDA1B1C1D1 – куб. АВ =  см. Тогда …Тест по теме: «Скалярное произведение векторов» Вариант №1 1.  Тогда угол между векторами и …1) острый; 2) тупой; 3) прямой. 2. DABC – тетраэдр, AB = BC = AC = AD = BD = CD. Тогда неверно, что… 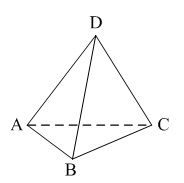 1)  2)  3)  3. Какое утверждение верное? 1)  2)  3)  4. Скалярное произведение векторов  и  равно…1) a1a2a3 + b1b2b3; 2) a1b1 + a2b2 + a3b3; 3) a1b2b3 + b1a2b3 + b1b2a3 Уровень В 1. Скалярное произведение векторов  и  равно…2.    Тогда m = …3. В правильной четырёхугольной пирамиде FABCD все рёбра равны по 2 см. Тогда 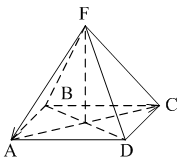 … 4. Угол между векторами  и  равен…5. Даны координаты точек: А (1; –1; –4), В (–3; –1; 0), С (–1; 2; 5), D (2; –3; 1). Тогда косинус угла между прямыми АВ и CD равен… Тест по теме: «Скалярное произведение векторов» Вариант №2 1.  Тогда угол между векторами и …1) острый; 2) тупой; 3) прямой. 2. ABCA1B1C1 – призма, 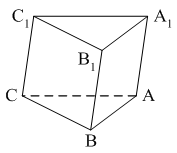 AB = BC = AC = AA1. Тогда верно, что… 1)  2)  3)  3. Какое утверждение верное? 1)  2)  3)  4. Скалярное произведение векторов  и  равно…1) m1n1 + m2n2 + m3n3; 2) (n1 – m1)2 + (n2 – m2)2 + (n3 – m3)2; 3) m1m2m3 + n1n2n3. Уровень В 1. Скалярное произведение векторов  и  равно…2.   Тогда n = …3. Все рёбра тетраэдра равны по 2 см. M, N, K, P – середины рёбер CD, BC, AB и BD соответственно. Тогда 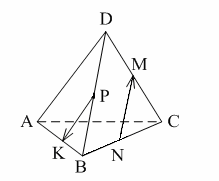 … 4. Угол между векторами  и  равен…5. Даны координаты точек: С (3; –2; 1), D (–1; 2; 1), M (2; –3; 3), N (–1; 1; –2). Тогда косинус угла между прямыми CD и MN равен… |