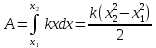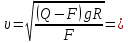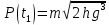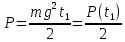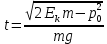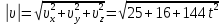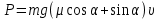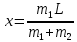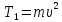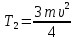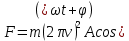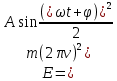контрольная работа. Тесты т 12 т 6 6 20 12
 Скачать 317.28 Kb. Скачать 317.28 Kb.
|
|
Контрольная № 1
Тесты
Задачи
Тесты ТМ1.12 Если тело массой m=1 кг движется со скоростью υ=10 м/с по окружности, то модуль изменения скорости тела при прохождении половины окружности равен 1) 0 м/с 2) 5м/с 3) 10 м/с 4) 15 м/с 5) 20 м/с  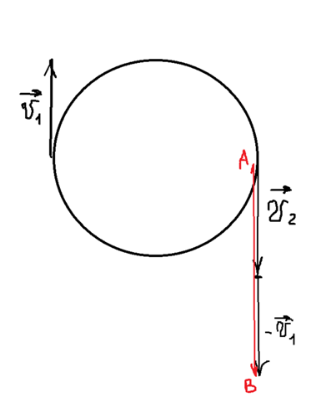 Дано: Решение: Дано: Решение:При прохождении половины окружности, вектор скорости будет направлен как показано на рисунке, тогда: 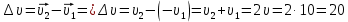 м/с м/сОтвет:20 м/с (5) ТМ3.6 Если шар радиусом R=50 см вращается согласно уравнению ω(t)=–5t+lnt, рад/с, то угол поворота φ шара за время t=4 секунды после начала движения 1) 29,5 рад 2) 31 рад 3) 33,5 рад 4) 36 рад 5) 38,5 рад 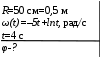 Дано: Решение: Дано: Решение:Угловая скорость по определению: 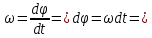 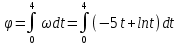 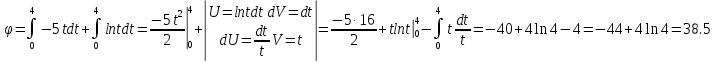 рад радОтвет: φ=35,5 рад (5) Т1.6 Если автомобиль первую половину пути двигался со скоростью 60 км/ч, а вторую 120 км/ч, то средняя скорость равна 1) 90 км/ч 2) 80 км/ч 3) 70 км/ч 4) 85 км/ч 5) 60 км/ч 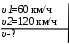 Дано: Решение: Дано: Решение: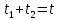 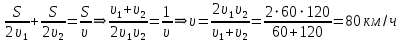 Ответ: υ=80 км/ч (2) Т1.20. Если автомобиль при экстренном торможении за 2 с уменьшил скорость с 72 км/ч до 36 км/ч, то за это время он прошел путь равный 1) 30 м 2) 18 м 3) 108 м 4) 40 м 5) 50 м 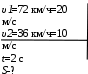 Дано: Решение: Дано: Решение:По определению ускорение: 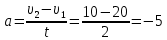 м/с2 м/с2Тогда: 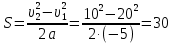 м мОтвет: S=30 м (1) Т3.12 Если самолет движется в горизонтальной плоскости по окружности радиусом 1200 м, имея центростремительное ускорение 12 м/с2 и кинетическую энергию 58 МДж, то его масса равна 1) 3,5·103 кг 2) 4,8·103 кг 3) 7,2·103 кг 4) 8,1·103 кг 5) 6,7·103 кг Дано: Решение: 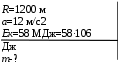 По определению кинетическая энергия: По определению кинетическая энергия: 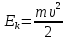 Центростремительное ускорение: 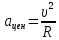 Тогда: 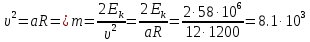 кг кгОтвет: m=8.1·103 кг (4) Т3.42 Если тело 0,3 кг движется по окружности радиусом 2,4 м с зависящим от времени центростремительным ускорением an=αt2 (α=0,33 м/с4), то после начала движения его импульс достигает значения 2,5 кг·м/с в момент времени, равный 1) 2,2 с 2) 5,3 с 3) 6,1 с 4) 8,2 с 5) 9,4 с Дано: Решение: 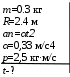 По определению импульс: По определению импульс: 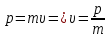 Центростремительное ускорение: 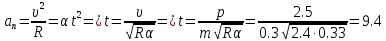 c cОтвет: t=9,4 с (5) Задачи М1.12 Длины векторов а=2 м и b=1 м, угол между ними α=60°. Найти скалярное произведение 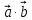 векторов. векторов.Дано: Решение: 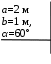 Скалярное произведение по определению: Скалярное произведение по определению: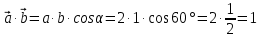 Ответ: 1 М3.4 Какую работу A надо затратить, чтобы растянуть пружину на x1=6 см, если сила F=1 Н растягивает ее на x2=1 см? Дано: Решение: 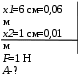 По закону Гука: По закону Гука: 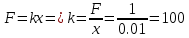 Работа по определению: 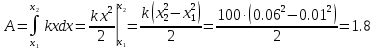 Дж ДжОтвет: А=1,8 Дж 1.27 По окружности радиусом R=5 м равномерно движется материальная точка со скоростью υ=5 м/с. Определить зависимость от времени пути s(t) и модуля вектора перемещения dr(t) от времени t Дано: Решение: 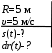 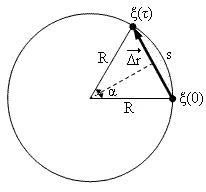 Длина пути, пройдённого по дуге окружности: Длина пути, пройдённого по дуге окружности: 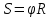 Угол поворота: 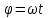 Угловая скорость: 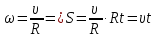 Модуль вектора перемещения: 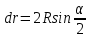 , , где 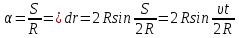 Ответ: 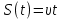 , , 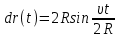 2.32 Летчик весом Q=780 H давит на сиденье кресла в нижней точке петли Нестерова с силой F=6,25 кН. Определить скорость υ самолета при радиусе петли R=250 м Дано: Решение: 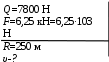 На летчика в нижней точке петли действуют сила тяжести F и сила давления кресла на летчика N. По второму закону Ньютона: На летчика в нижней точке петли действуют сила тяжести F и сила давления кресла на летчика N. По второму закону Ньютона: 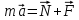 В проекции на ось y: 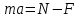 Центростремительное ускорение: 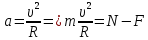 Сила тяжести по определению: 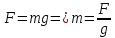 . По третьему закону Ньютона: N=Q. Тогда: . По третьему закону Ньютона: N=Q. Тогда: 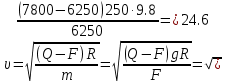 м/с м/сОтвет: υ=24,6 м/с 3.12 Тело массой m=450 г брошено со скоростью υ0=16,8 м/с горизонтально поверхности земли с высоты h=24 м. Найти мгновенную мощность P(t) его силы тяжести в момент падения на землю и среднюю мощность P за время движения тел. 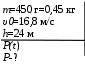 Дано: Решение: Дано: Решение: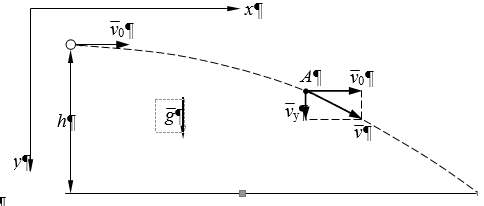 Так как на тело действует только сила тяжести, горизонтальная составляющая скорости не изменяется и равна υx=υ0. Вертикальная составляющая скорости изменяется по закону 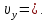 Путь по вертикали: 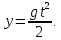 В момент падения t1 путь равен h: 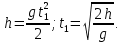 Мгновенная мощность силы тяжести: 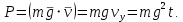 В момент падения мощность силы тяжести равна 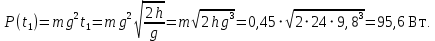 Средняя мощность за время падения: 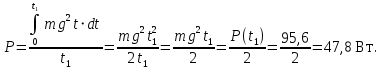 Ответ: P(t1)=95,6 Вт; Р=47,8 Вт. 3.42 Тело массой m=0,25 кг брошено горизонтально c некоторой высоты. Найти момент времени t, когда кинетическая энергия достигает значения Ek=218 Дж, если в момент броска импульс тела p0=5 кг·м/с Дано: Решение: 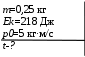 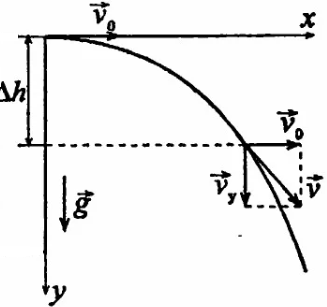 В момент времениt кинетическая энергия тела: 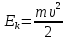 Так как вертикальная составляющая скорости изменяется по закону 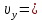 , то скорость в момент времениt: , то скорость в момент времениt: 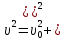 .Тогда: .Тогда: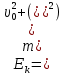 По условию задачи, импульс тела в момент броска: 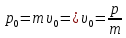 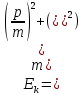 c cОтвет: t=8.3 c Вопросы 24-3. Изменится ли результат скалярного произведения двух векторов, если поменять местами перемножаемые вектор. Скалярное произведение по определению: 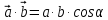 . Поэтому, если поменять местами перемножаемые вектора, результат не изменится. . Поэтому, если поменять местами перемножаемые вектора, результат не изменится.36-5-1,6. Пользуясь таблицей производных и основными правилами дифференцирования, найдите производные от следующих функций: 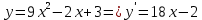 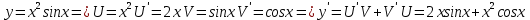 80-4. Запишите выражения для векторов скорости и ускорения материальной точки в декартовой системе координат. Вектор скорости: 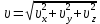 Ускорение: 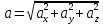 113-5. Запишите второй закон Ньютона с использованием понятий силы, импульса силы, импульса тела. 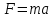 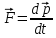 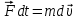 152-10. Дайте графическую интерпретацию работы, откладывая вдоль вертикальной оси значения проекции силы на направление перемещения, а вдоль другой оси-пройденное телом расстояние 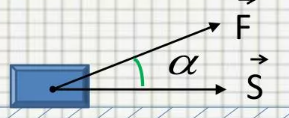 180-13. Выведете математические условия для нахождения системы в состоянии устойчивого и неустойчивого равновесия. 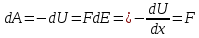 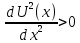 -равновесие устойчиво -равновесие устойчиво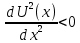 -равновесие неустойчиво -равновесие неустойчивоКонтрольная работа №2 Вращательное и колебательное движение
Тесты
Задачи
Тесты ТМ2.8 Если радиус-вектор материальной точки изменяется со временем по закону, 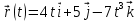 м, то модуль вектора ускорения точки в момент времени t=5 c равен м, то модуль вектора ускорения точки в момент времени t=5 c равен1) 200 м/с2 2) 205 м/с2 3) 210 м/с2 4) 215 м/с2 5) 220 м/с2 Дано: Решение:  По определению: По определению: 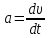 Скорость по определению: 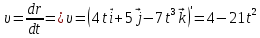 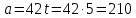 220 м/с2 220 м/с2Ответ: a=210 м/с2 (3) ТМ3.5 Если диск радиусом R=1 см вращается согласно уравнению ε(t)=3+8t-13sint, рад/с2, то нормальное ускорение an диска для момента времени t=1 с 1) 1,5 м/с2 2) 2,0 м/с2 3) 2,5 м/с2 4) 3,0 м/с2 5) 3,5 м/с2 Дано: Решение: 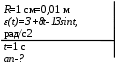 Нормальное ускорение по определению: Нормальное ускорение по определению: 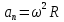 Угловая скорость: 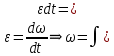 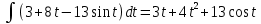 . Тогда . Тогда 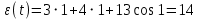 рад/с2. рад/с2.Поэтому: 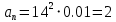 м/с2 м/с2Ответ: an=2 м/с2 (2) T4.12 Если частицы образуют механическую систему, то векторная сумма внутренних сил равна 1) ∞ 2) 0 3) 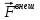 4) 4) 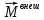 5) -∞ 5) -∞Векторная сумма всех внутренних сил в системе равна нулю. Ответ: 2 T5.13 Основное уравнение вращательного движения (I–момент инерции тела, εz и Miz–проекции вектора углового ускорения и момента i-ой силы, действующей на тело, на ось z)-это 1) 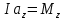 2) 2) 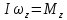 3) 3) 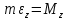 4) 4) 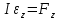 5) 5) 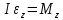 Ответ: 5 Т6.12 Если пружины с коэффициентами упругости 4 Н/м и 6 Н/м соединить последовательно, то коэффициент упругости системы пружин равен 1) 10 Н/м 2) 0,42 Н/м 3) 2,4 Н/м 4) 0,1 Н/м 5) 3,2 Н/м Дано: Решение: 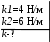 При последовательном соединении: При последовательном соединении: 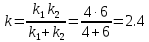 Н/м Н/мОтвет: k=2,4 Н/м (3) Т6.42 Если дифференциальное уравнение колебательного движения груза массой 3 кг имеет вид 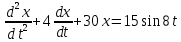 , то максимальное значение вынуждающей силы равно , то максимальное значение вынуждающей силы равно 1) 30 Н 2) 40 Н 3) 45 Н 4) 50 Н 5) 55 Н  Дано: Решение: Дано: Решение:Из уравнения: 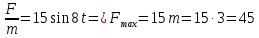 Н НОтвет: Fmax=45 Н (3) Задачи М1.4 Вектор скорости тела меняется со временем по закону 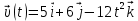 , м/с, где t-время; , м/с, где t-время; 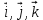 орты координатных осей. Найти модуль скорости в момент времени t=4 с. орты координатных осей. Найти модуль скорости в момент времени t=4 с.Дано: Решение:  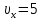 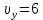 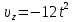 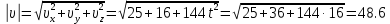 м/с м/сОтвет: |υ|=48,6 м/с М1.26 Автомобиль пытается въехать на гору с уклоном α=5°, но равномерно съезжает вниз со скоростью υ=2 м/с. Найти мощность P силы тяги, если масса автомобиля m=1000 кг, коэффициент трения μ=0,01.  Дано: Решение: Дано: Решение: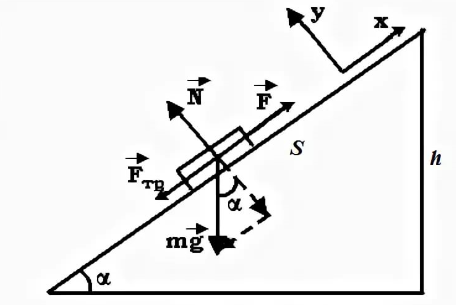 По второму закону Ньютона: 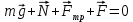 Проекция на ось X: 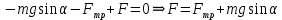 . . На ось Y: 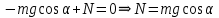 Сила трения: 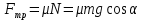 Сила тяги: 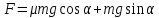 Мощность силы тяги: 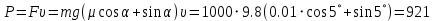 Вт ВтОтвет: Р=921 Вт 4.12 Два шарика массами m1=50 г и m2=100 г с отверстиями вдоль диаметра насажены на стержень и связаны друг с другом нитью так, что расстояние между их центрами L=20 см. Стержень помещен на центробежную машину с осью вращения перпендикулярно стержню. На каком расстоянии x от оси вращения надо расположить больший шарик, чтобы при вращении стержня шарики остались в равновесии. Дано: Решение: 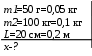 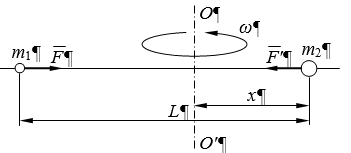 По второму закону Ньютона 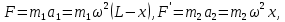 где F=F'-сила натяжения нити, ω-угловая скорость вращения стержня, a1, a2-нормальные ускорения первого и второго шаров соответственно. Приравняем силы: 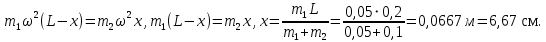 Ответ: x=6,67 см. 5.27 Обруч и сплошной цилиндр одинаковой массы m=5 кг катятся без скольжения с одинаковой скоростью υ=10 м/с. Найти кинетические энергии T1 и T2 этих тел Дано: Решение: 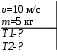 Обруч и цилиндр участвует в поступательном и вращательном движении одновременно: Обруч и цилиндр участвует в поступательном и вращательном движении одновременно: 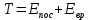 Где кинетическая энергия поступательного движения: 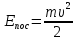 Кинетическая энергия вращательного движения: 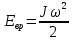 Момент инерции обруча: 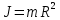 . Связь линейной и угловой скорости: υ=ωR. Тогда: . Связь линейной и угловой скорости: υ=ωR. Тогда: 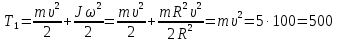 Дж ДжМомент инерции сплошного цилиндра: 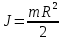 . .Тогда: 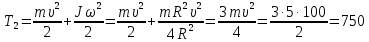 Дж ДжОтвет: T1=500 Дж, T2=750 Дж 6.38 Материальная точка с массой m=25 г совершает гармонические колебания с амплитудой A=10 см и частотой ν=1 Гц. Определить кинетическую энергию и действующую на нее силу в тот момент, когда ее смещение от положения равновесия составляет x=5 см? Дано: Решение: 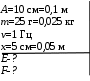 Уравнение гармонических колебаний в общем виде имеет вид: Уравнение гармонических колебаний в общем виде имеет вид: 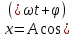 , где , где 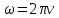 -круговая частота. -круговая частота. Скорость точки, совершающей колебания: 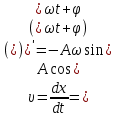 Ускорение точки: 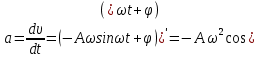 Сила определяется: 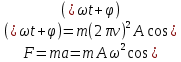 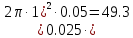 мН мНКинетическая энергия: 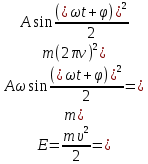 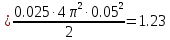 мДж мДжОтвет: Е=1,23 мДж,F=49,3 мН 6.137 Уравнение колебаний, создаваемых источником, 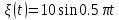 . Записать уравнение колебания для точки волны в момент t=4 с после начала колебаний. . Записать уравнение колебания для точки волны в момент t=4 с после начала колебаний.Дано: Решение:  Уравнение плоской волны в общем виде: Уравнение плоской волны в общем виде: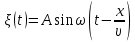 Тогда: 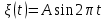 Ответ: 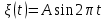 Вопросы 19-7 Как найти длину вектора 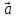 , зная его проекции ax, ay, az на координатные оси? , зная его проекции ax, ay, az на координатные оси?Длина вектора: 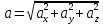 252-1 Дайте определение равнодействующей сил, приложенных к абсолютно твердому телу Равнодействующей сил, приложенных к твердому телу, силу равную сумме сил, действующих на твердое тело момент которой относительно произвольной точки О равен сумме моментов всех сил относительно этой точки. 281-4 В каком случае проекция ненулевого момента силы, лежащей в плоскости ХОУ, на ось z равна нулю? Момент равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси; 295-7 Сформулируйте теорему Штейнера. Теорема Штейнера: Момент инерции I тела относительно некоторой оси z равен моменту инерции IC тела относительно оси z' параллельной z, и проходящей через центр масс тела, плюс произведение массы m тела на квадрат расстояния а между осями: 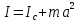 345-4 Циклическая частота затухающих колебаний ω больше или меньше собственной частоты ω0? Частота ω затухающих колебаний меньше частоты ω0собственных незатухающих колебаний из-за действия тормозящей силы сопротивления. 373-1 Почему незатухающие колебания в реальных системах могут быть только вынужденными? Так как в реальных системах они с течением времени затухают. |