Тестирование ПО. РИС-18-1б_СавинСА_ЛР1. Тестирование базового пути
 Скачать 125 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Пермский национальный исследовательский политехнический университет Кафедра ИТАС ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 1 по дисциплине «Тестирование программного обеспечения» Тема: Тестирование базового пути Вариант №17 Выполнил студент гр. РИС-18-1б Савин Сергей Алексеевич Проверил доцент кафедры ИТАС Полевщиков Иван Сергеевич Пермь, 2021 год Задание к работе 1) Для каждой из двух задач написать консольное приложение на одном из языков программирования высокого уровня (например, Java, C#, C++) в соответствии с постановкой задачи (по вариантам). В программах входные данные должны вводиться пользователем с клавиатуры. 2) Провести тестирование каждого консольного приложения способом тестирования базового пути: а) построить потоковый граф на основе пронумерованного текста программы; б) вычислить цикломатическую сложность графа (по каждой из трех формул); в) определить базовое множество независимых линейных путей; г) подготовить тест-кейсы, инициирующие выполнение каждого пути (для каждого тест-кейса формируются входные данные и ожидаемые результаты); д) сравнить реальные результаты каждого тест-кейса с ожидаемыми. Задача №1 1.1 Постановка задачи Написать программу, заменяющую меньшее из двух чисел и их средним арифметическим, а большее – средним геометрическим их модулей. В случае, если числа равны, то производить замену не требуется. Входные данные: вещественные числа x и y. Данные, выводимые на экран: значения чисел и после замен. 1.2 Пронумерованный текст программы на языке Python  1.3 Потоковый граф 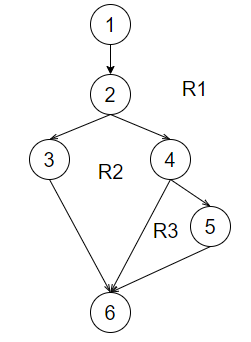 1.4 Вычисление цикломатической сложности потокового графа по трем формулам 1) Потоковый граф имеет 3 региона (  ,  ,  ), следовательно, цикломатическая сложность равнаV(G) = 3.2) Количество дуг в потоковом графе равноE=7, а количество вершин – N=6, следовательно, согласно формуле (1), цикломатическая сложность равна: V(G)=E-N+2=7-6+2=3 3) Количество предикатных узлов в потоковом графе равно p=2, следовательно, согласно формуле (2), цикломатическая сложность равна: V(G)=p+1=2+1=3. 1.5Базовое множество независимых линейных путей Путь 1: 1-2-3-6 Путь 2: 1-2-4-6 Путь 3: 1-2-4-5-6 1.6 Тест-кейсы, инициирующие выполнение каждого пути
Из таблицы можно сделать вывод, что для каждого тест-кейса реальный результат работы программы удовлетворяет ожидаемому. Задача №2 2.1 Постановка задачи Написать программу для вычисления значения выражения:  Входные данные: целое число  .Данные, выводимые на экран: значение выражения, либо сообщение «Входные данные не верны!» (при  ).2.2 Пронумерованный текст программы на языке Python 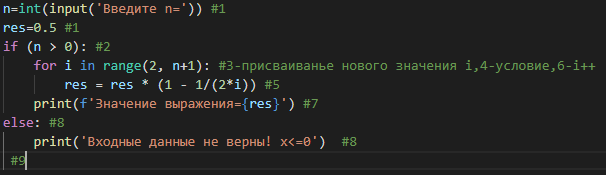 2.3 Потоковый граф 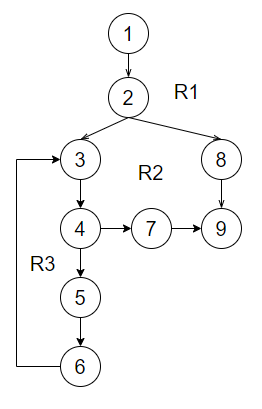 2.4 Вычисление цикломатической сложности потокового графа по трем формулам 1) Потоковый граф имеет 3 региона ( , ), следовательно, цикломатическая сложность равнаV(G) = 3.2) Количество дуг в потоковом графе равноE=10, а количество вершин – N=9, следовательно, согласно формуле (1), цикломатическая сложность равна: V(G)=E-N+2=10-9+2=3 3) Количество предикатных узлов в потоковом графе равно p=2, следовательно, согласно формуле (2), цикломатическая сложность равна: V(G)=p+1=2+1=3. 2.5Базовое множество независимых линейных путей Путь 1: 1-2-8-9 Путь 2: 1-2-3-4-5-6-3-…-3-4-7-9 Путь 3: 1-2-3-4-7-9 2.6 Тест-кейсы, инициирующие выполнение каждого пути
Из таблицы можно сделать вывод, что для каждого тест-кейса реальный результат работы программы удовлетворяет ожидаемому. |