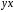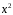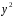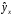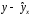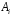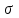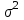Тестовые задания Парная регрессия и корреляция Наиболее наглядным видом выбора уравнения парной регрессии является
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
Вопросы к экзамену Определение эконометрики. Эконометрический метод и этапы эконометрического исследования. Парная регрессия. Способы задания уравнения парной регрессии. Линейная модель парной регрессии. Смысл и оценка параметров. Оценка существенности уравнения в целом и отдельных его параметров ( 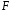 -критерий Фишера и -критерий Фишера и 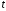 -критерий Стьюдента). -критерий Стьюдента).Прогноз по линейному уравнению регрессии. Средняя ошибка аппроксимации. Нелинейная регрессия. Классы нелинейных регрессий. Регрессии нелинейные относительно включенных в анализ объясняющих переменных. Регрессии нелинейные по оцениваемым параметрам. Коэффициенты эластичности для разных видов регрессионных моделей. Корреляция и 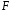 -критерий Фишера для нелинейной регрессии. -критерий Фишера для нелинейной регрессии.Отбор факторов при построении уравнения множественной регрессии. Оценка параметров уравнения множественной регрессии. Множественная корреляция. Частные коэффициенты корреляции. 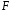 -критерий Фишера и частный -критерий Фишера и частный 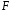 -критерий Фишера для уравнения множественной регрессии. -критерий Фишера для уравнения множественной регрессии.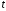 -критерий Стьюдента для уравнения множественной регрессии. -критерий Стьюдента для уравнения множественной регрессии.Фиктивные переменные во множественной регрессии. Предпосылки МНК: гомоскедастичность и гетероскедастичность. Предпосылки МНК: автокорреляция остатков. Обобщенный МНК. Общие понятия о системах эконометрических уравнений. Структурная и приведенная формы модели. Проблема идентификации. Необходимое условие идентифицируемости. Проблема идентификации. Достаточное условие идентифицируемости. Методы оценки параметров структурной формы модели. Основные элементы временного ряда. Автокорреляция уровней временного ряда и выявление его структуры. Моделирование сезонных колебаний: аддитивная модель временного ряда. Моделирование сезонных колебаний: мультипликативная модель временного ряда. Критерий Дарбина-Уотсона. Варианты индивидуальных заданий D.1. Парная регрессия и корреляция Пример. По территориям региона приводятся данные за 199X г. Таблица D.1
Требуется: Построить линейное уравнение парной регрессии 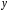 от от 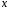 . .Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации. Оценить статистическую значимость параметров регрессии и корреляции с помощью 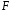 -критерия Фишера и -критерия Фишера и 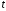 -критерия Стьюдента. -критерия Стьюдента.Выполнить прогноз заработной платы 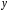 при прогнозном значении среднедушевого прожиточного минимума при прогнозном значении среднедушевого прожиточного минимума 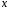 , составляющем 107% от среднего уровня. , составляющем 107% от среднего уровня.Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. На одном графике построить исходные данные и теоретическую прямую. Решение Для расчета параметров уравнения линейной регрессии строим расчетную таблицу D.2. Таблица D.2
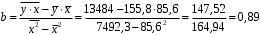 ; ;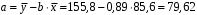 . .Получено уравнение регрессии: 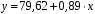 . .С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,89 руб. Тесноту линейной связи оценит коэффициент корреляции: 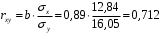 ; ; 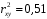 . .Это означает, что 51% вариации заработной платы ( 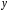 ) объясняется вариацией фактора ) объясняется вариацией фактора 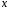 – среднедушевого прожиточного минимума. – среднедушевого прожиточного минимума.Качество модели определяет средняя ошибка аппроксимации: 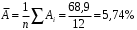 . .Качество построенной модели оценивается как хорошее, так как 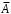 не превышает 8-10%. не превышает 8-10%.Оценку значимости уравнения регрессии в целом проведем с помощью 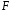 -критерия Фишера. Фактическое значение -критерия Фишера. Фактическое значение 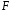 -критерия: -критерия: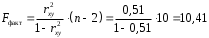 . .Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы 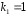 и и 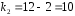 составляет составляет 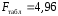 . Так как . Так как 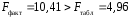 , то уравнение регрессии признается статистически значимым. , то уравнение регрессии признается статистически значимым. Оценку статистической значимости параметров регрессии проведем с помощью 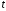 -статистики Стьюдента и путем расчета доверительного интервала каждого из показателей. -статистики Стьюдента и путем расчета доверительного интервала каждого из показателей.Табличное значение 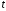 -критерия для числа степеней свободы -критерия для числа степеней свободы 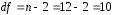 и и 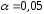 составит составит 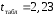 . .Определим случайные ошибки 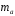 , , 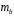 , , 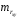 : :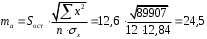 ; ;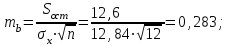 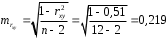 . .Тогда 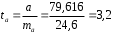 ; ;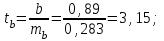 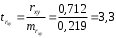 . .Фактические значения 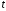 -статистики превосходят табличное значение: -статистики превосходят табличное значение: 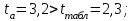 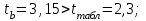 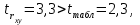 поэтому параметры 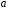 , , 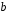 и и 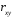 не случайно отличаются от нуля, а статистически значимы. не случайно отличаются от нуля, а статистически значимы.Рассчитаем доверительные интервалы для параметров регрессии 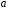 и и 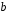 . Для этого определим предельную ошибку для каждого показателя: . Для этого определим предельную ошибку для каждого показателя: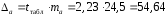 ; ;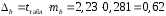 . .Доверительные интервалы 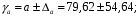 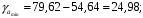 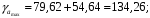 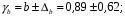 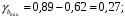 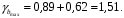 Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 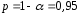 параметры параметры 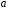 и и 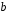 , находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля. , находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит: 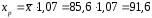 руб., тогда прогнозное значение заработной платы составит: руб., тогда прогнозное значение заработной платы составит: 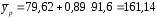 руб. руб.Ошибка прогноза составит: 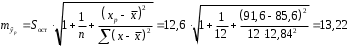 . .Предельная ошибка прогноза, которая в 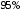 случаев не будет превышена, составит: случаев не будет превышена, составит: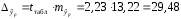 . .Доверительный интервал прогноза: 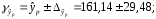 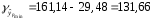 руб.; руб.;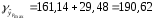 руб. руб.Выполненный прогноз среднемесячной заработной платы является надежным ( 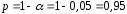 ) и находится в пределах от 131,66 руб. до 190,62 руб. ) и находится в пределах от 131,66 руб. до 190,62 руб.В заключение решения задачи построим на одном графике исходные данные и теоретическую прямую (рис. D.1): 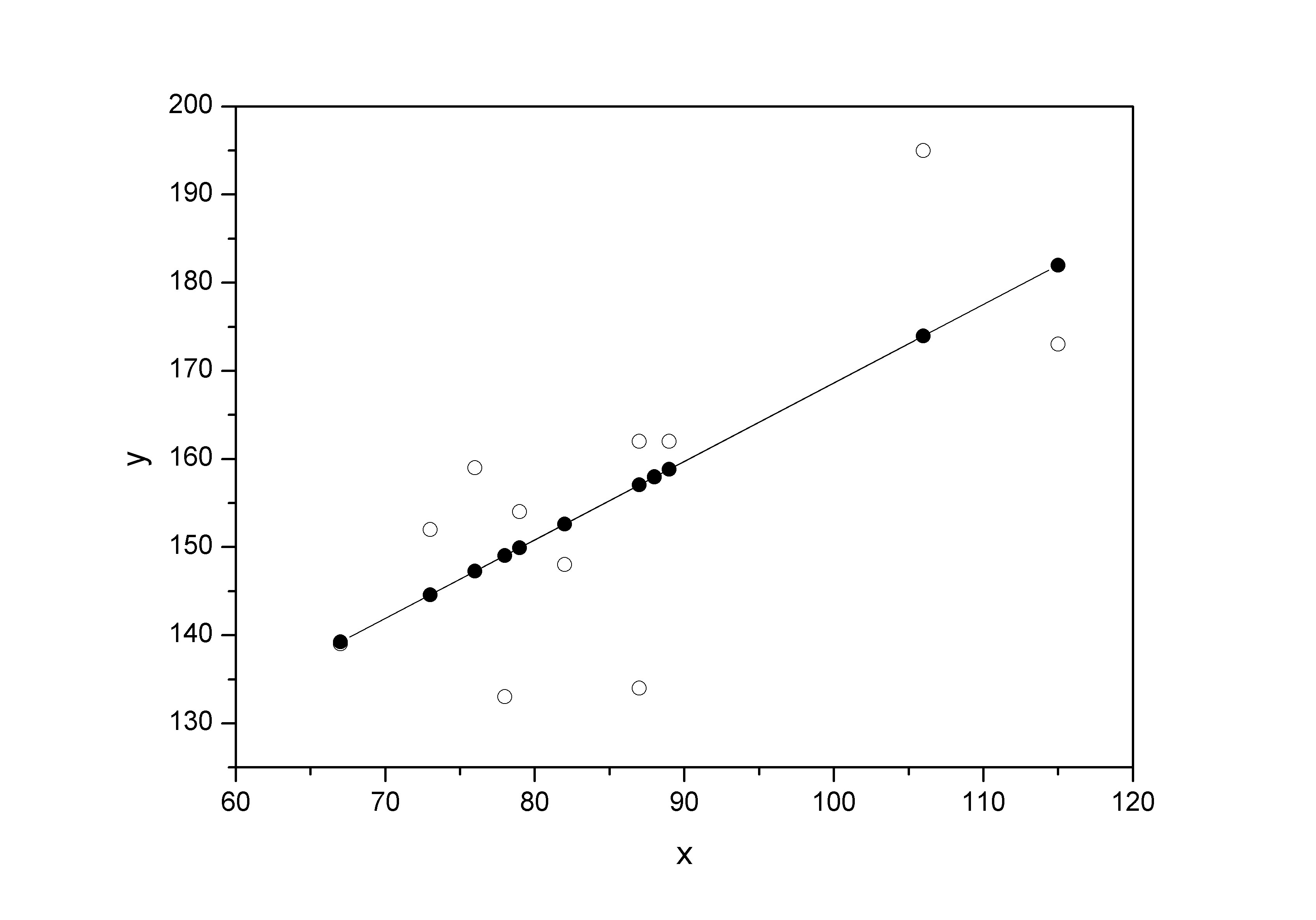 Рис. D.1. |