Модель гировертикали. Автоматизация и управление - Модель гировертикали в программе MA. The model is gyroverted in the matlab program student Shilin Dmitry Andreevich
 Скачать 335.12 Kb. Скачать 335.12 Kb.
|
|
УДК 681.2-5 THE MODEL IS GYROVERTED IN THE MATLAB PROGRAM Student Shilin Dmitry Andreevich, associate Professor Krivosheev Sergey Valentinovich, KNRTU-KAI Kazan, Russian Federation Abstract. In this paper, a real model of G B was modeled in MatLab (Simulink) with the specified motion parameters. I.e., all the considered options with the parameters and calculated coefficients are given. Keywords: acceleration, gyrovertical, precessional, correction, moment, error. МОДЕЛЬ ГИРОВЕРТИКАЛИ В ПРОГРАММЕ MATLAB студент Шилин Дмитрий Андреевич, доцент Кривошеев Сергей Валентинович, КНИТУ-КАИ г. Казань, Российская Федерация Аннотация. В данной работе была промоделирована в MatLab (Simulink) реальная модель ГВ при заданных параметрах движения. Т.е. все рассмотренные варианты с приведены параметрами и рассчитанными коэффициентами. Ключевые слова: ускорение, гировертикаль, прецессионные, коррекция, момент, погрешность. В модели программы используется система уравнений гировертикали: 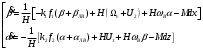 (1) (1)Ниже представлены листинг программы и модель в программе Matlab(Simulink)(рис.1), в которых происходит моделирование прецессионных уравнений движения гировертикали: %исходные данные H=4000; %кинетический момент гироскопа[Нмс] g=9.8; %ускорение свободного падения[м/с^2] dV=0.1*g; Fi=30/57.3; %угол[рад] V=1000/3.6; %скорость [м/с] Am=12/60/57.3; [угл.мин.] Bm=12/60/57.3; [угл.мин.] Ay=Am/2; %статические погрешности By=Bm/2; %статические погрешности Mdx=0.8; %моменты трения в подшипниках оси х относительно рамки карданова подвеса[Н*м] Mdz=0.5; %моменты трения в подшипниках оси z относительно рамки карданова подвеса[Н*м] R=6.371*10^6; %радиус земли [м] U=7.29*10^-5; %угловая скорость вращения земли[1/c] Ug=U*cos(Fi); %горизонтальная составляющая скорости земли Psi0=30/57.3; %угол[рад] WB=1/57.3; %WB=0; %угловая скорость виража[рад/с] Wv=V/R; %Угловая скорость от облета земли U1m=U*cos(Fi); %горизонтальные составляющие угловой скорости вращения земли U2m=U*cos(Fi); %горизонтальные составляющие угловой скорости вращения земли k1=(H/By)*(Wv+U2m+(Mdx/H)) % коэффициент, зависящий от параметров датчика k2=(H/Ay)*((Mdz/H)+U1m) % коэффициент, зависящий от параметров датчика Tk1=H/k1; %Постоянные времени цепей коррекции Tk2=H/k2; %Постоянные времени цепей коррекции Blv=atan(dV/g) %Blv=0; %угол ложной вертикали Alv=atan((V*WB)/g) %Alv=0; %угол ложной вертикали 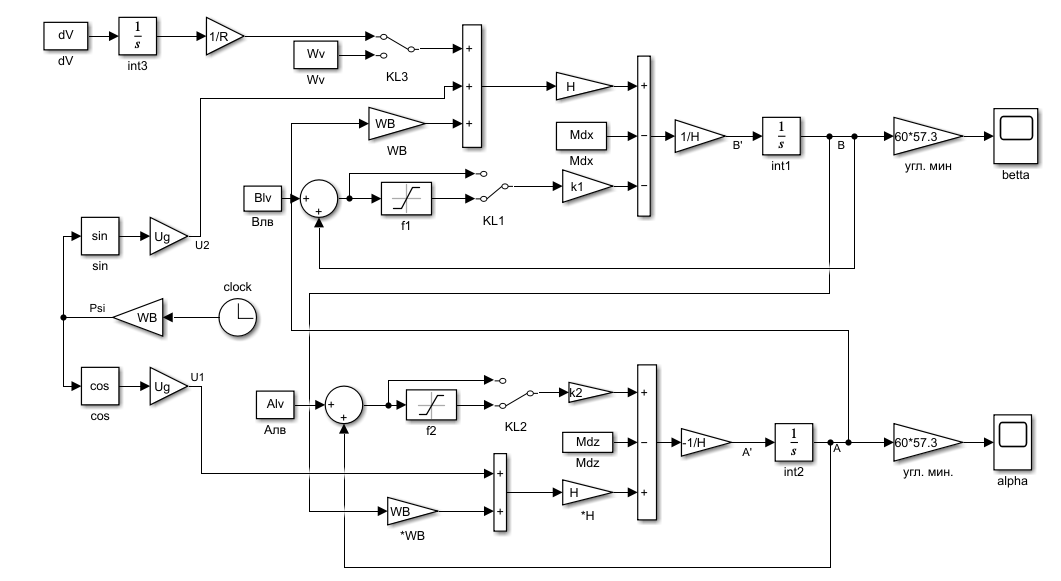 Рис.1. Модель гировертикали в программе Matlab(Simulink) Ниже представлено 4 случая работы данной системы: 1. Прямолинейный полет с отсутствием виража и ускорения( 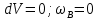 ) (рис.1, рис.2) ) (рис.1, рис.2) 2. Прямолинейный полет с виражом и без ускорения ( 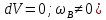 (рис.3, рис.4) (рис.3, рис.4)3. Прямолинейный полет без виража и c ускорением ( 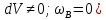 (рис.5, рис.6) (рис.5, рис.6)4. Прямолинейный полет с виражом и с ускорением ( 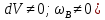 (рис.7, рис.8) (рис.7, рис.8)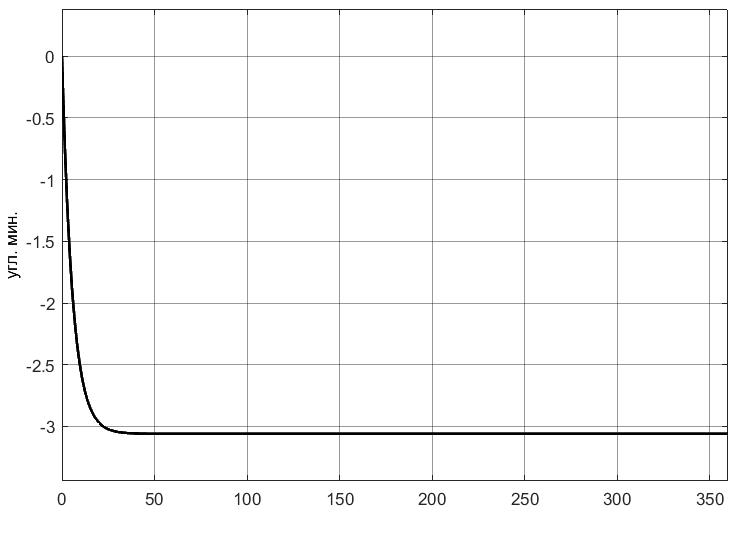 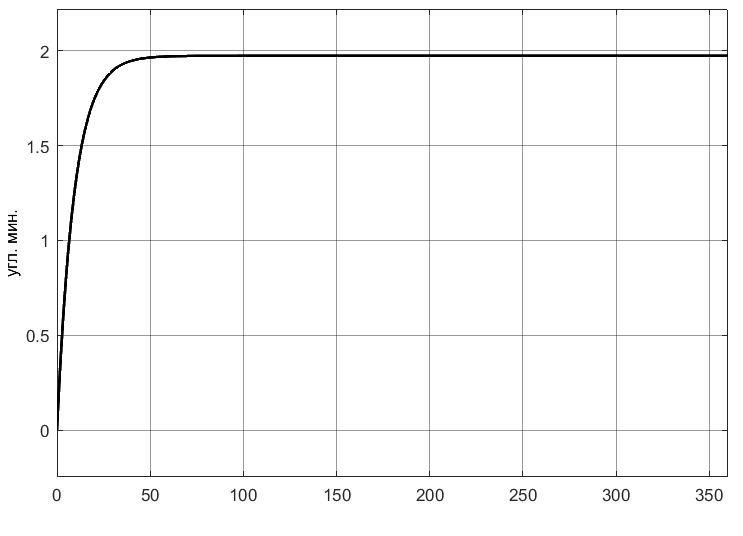 5. Исследование влияния величины угловой скорости виража 5. Исследование влияния величины угловой скорости виража 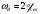 , когда модуль путевой скорости постоянен(рис.9, рис.10) , когда модуль путевой скорости постоянен(рис.9, рис.10)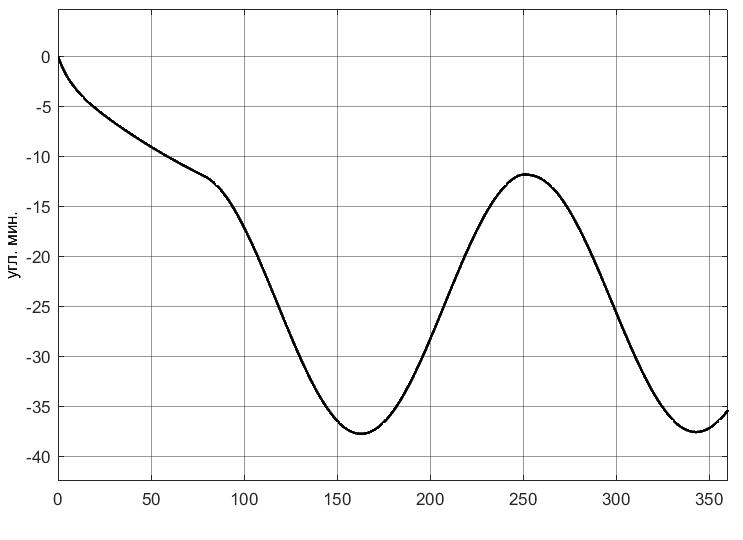 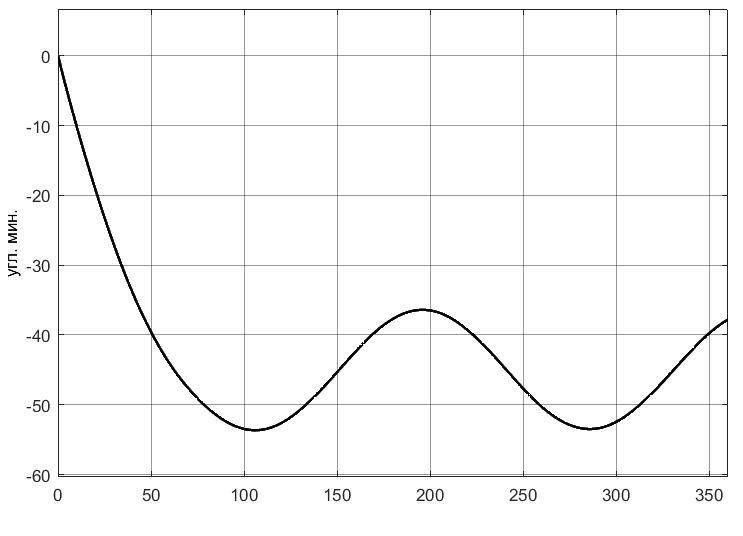 Рис.1. График изменения угла β Рис.1. График изменения угла β  Рис.2. График изменения угла α Рис.2. График изменения угла α Рис.3. График изменения угла β Рис.4. График изменения угла α 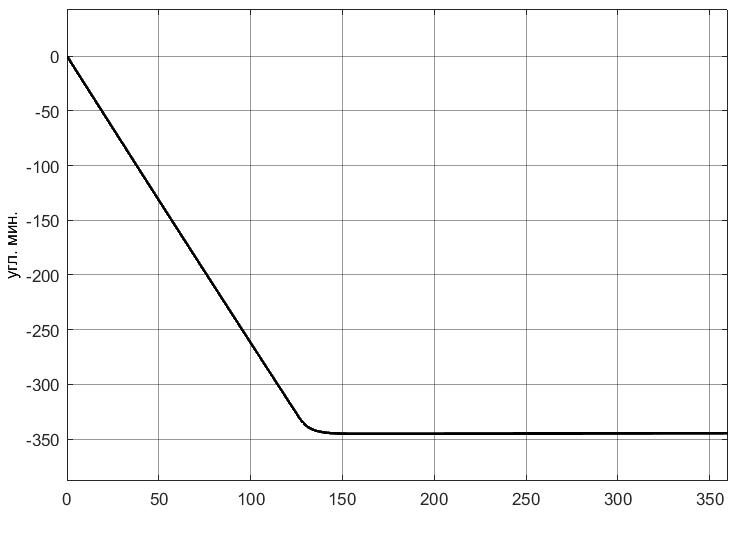   Рис.5. График изменения угла β Рис.6. График изменения угла α  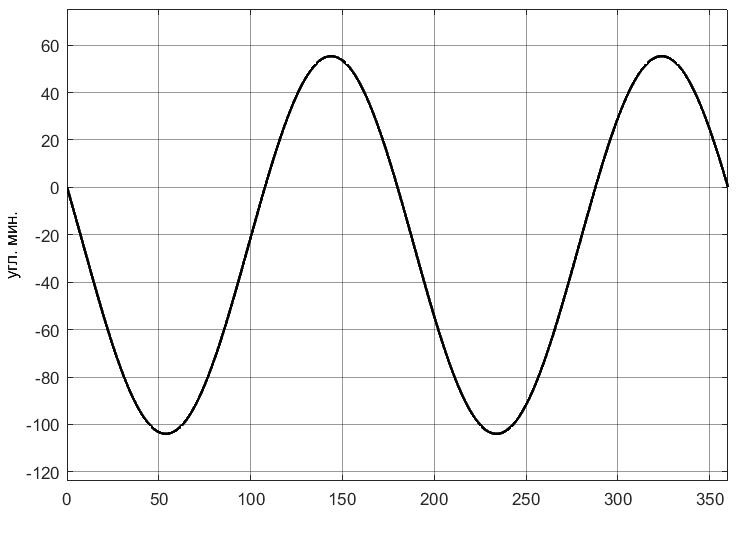 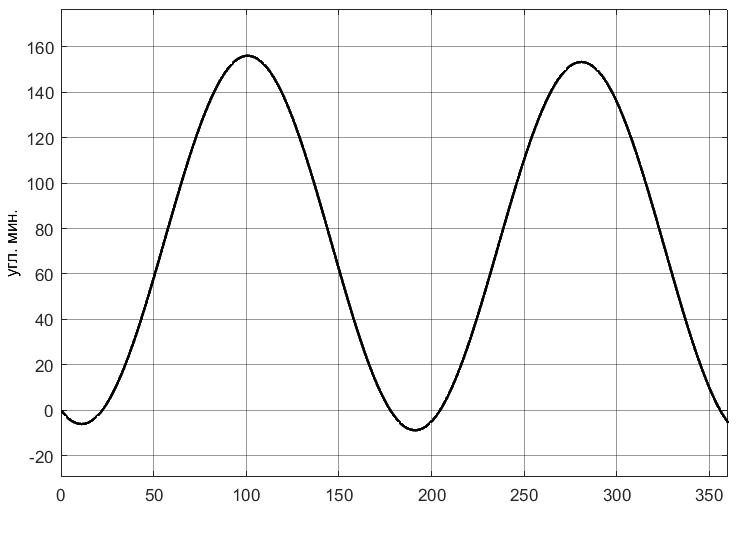 Рис.7. График изменения угла β Рис.8. График изменения угла α Рис.7. График изменения угла β Рис.8. График изменения угла αРис.9. График изменения угла β Рис.10. График изменения угла α По полученным прецессионным уравнениям была составлена модель ГВ в программе Matlab(Simulink), описывающая поведение ГВ в горизонтальном полете при различном маневрировании. В данной работе рассмотрены разные случаи маневрирования: в режиме прямолинейного полета без виража и ускорения, в режиме прямолинейного полета с виражом и без ускорения и прямолинейный полет без виража и c ускорением. Была определена зависимость угла от угловой скорости виража. 1. Прямолинейное ускоренное движение с постоянным модулем путевой скорости и отсутствием угловой скорости Установившиеся значение определяется моментами дрейфа, проекции угловых скоростей от вращения и облета земли, а также крутизной контуров коррекции, которые в данном случае работают в линейной зоне. 2. Движение в плоскости горизонта, представляющее разворот с угловой скоростью, когда модуль путевой скорости постоянен При длительном вираже среднее значение по углу α = 25 угл. мин., а по углу β=45 угл. мин. Относительно этих значений происходят колебания с амплитудами 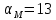 и периодом Т=170 и периодом Т=170 3. Движение в плоскости горизонта, представляющее разворот без угловой скоростью 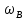 , когда модуль путевой скорости не постоянен. , когда модуль путевой скорости не постоянен.Установившиеся значение определяется моментами дрейфа, проекции угловых скоростей от вращения и облета земли, а также крутизной контуров коррекции, которые в данном случае работают в линейной зоне. 4. Движение в плоскости горизонта, представляющее разворот с угловой скоростью, когда модуль путевой скорости не постоянен При длительном вираже среднее значение по углу α = 70 угл. мин., а по углу β=20 угл. мин. Относительно этих значений происходят колебания с амплитудами 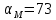 и периодом Т=100 и периодом Т=100 5. Прямолинейное ускоренное движение с постоянным модулем путевой скорости и отсутствием угловой скорости с постепенным увеличением повышения угловой скорости. References: 1. Mikhailov O. I., Kozlov I. M., Gergel F. S. Aviasionnie pribory M, “Machinostroenie” (транслит.) [Aviation devices M, “Mechanical Engineering"(англ.)], 1977. – 416 p. – Text: direct. (in Russian). 2. Pel'por D. S. Giroskopicheskie sistemy (транслит.) [Gyroscopic Systems(англ.)], 1986. – 422 p. – Text: direct. (in Russian). 3. Danilin V. P. Giroskopicheskie pribory (транслит.) [Gyroscopic devices (англ.)], 1965. – 538s. 4. Vinogradov G. M., Krivosheev S. V. Dinamicheski nastraivaemye giroskopy (транслит.) [Dynamically adjustable gyroscopes (англ.)], 2008. – 127s. Список литературы: 1. Михайлов О. И., Козлов И. М., Гергель Ф. С. Авиационные приборы М, “Машиностроение”, 1977. – 416 с. – Текст : непосредственный. 2. Пельпор Д. С. Гироскопические системы, 1986. – 422с. – Текст : непосредственный. 3. Данилин В. П. Гироскопические приборы, 1965. – 538с. – Текст : непосредственный. 4. Виноградов Г. М., Кривошеев С. В. Динамически настраиваемые гироскопы, 2008. – 127с. – Текст : непосредственный. |
