лаба по ЭММиМ. лаб 1-В5-Лазарев. Тические методы и модели на тему Регрессионный анализ производительности труда
 Скачать 361 Kb. Скачать 361 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ Федеральное государственное бюджетное образовательное учреждение высшего образования «Рязанский государственный радиотехнический университет имени В.Ф. Уткина» Инженерно – экономический факультет Кафедра ГМКУ Лабораторная работа №1 по дисциплине «Экономическо-математические методы и модели» на тему «Регрессионный анализ производительности труда» Вариант №5 Выполнили: студенты группы 9715 Лазарев Д.Н., Муталиев М.Я., Колядич О.С., Чибисов А.П. Проверили: к.т.н., доцент кафедры ГМКУ Федотов Н.И., ст. преподаватель кафедры ГМКУ Меркулов Ю.А. Рязань, 2021 Цель работы: построение регрессионной модели производительности труда и её анализ. Перечень факторов влияющих на производство труда и соответствующих требованиям: Х1- уровень фондовооруженности; Х2- уровень технологии; Х3- коэффициент текучести; Х4- удельный вес материальных затрат; Х5- средний возраст оборудования; Х6- индекс товарной продукции; Х7- удельный вес новой продукции; Х8- удельный вес продукции, сдаваемой с первого предъявления; Х9- уровень коэффициента ритмичности и другие. Сбор и систематизация информация. 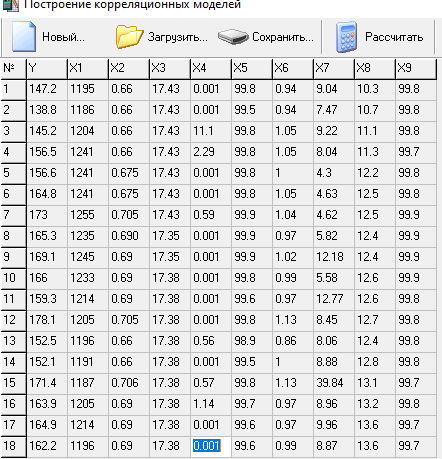 Рисунок 1: вариант исходных данных Статистическая оценка значимости факторов. 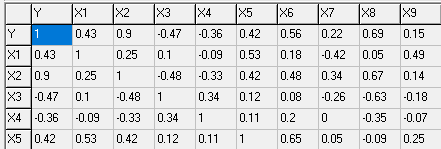 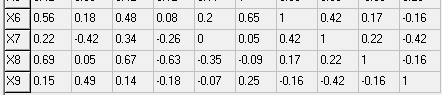 Рисунок 2: Оценка значимости факторов На первом этапе необходимо рассмотреть коэффициенты корреляции между результативным признаком и факторным rхixj. Граничное значение коэффициента корреляции в нашем случае равно 0.3. Факторы для которых rхixj >0.3 в модель включается, остальные не включаются. На основании этого выделяем факторы X1= 0.43; Х2=0,9, X5=0.42; X6=0.56; X8=0,69. На второй этапе нам необходимо отобрать факторы по значению коэффициента детерминации, значение которого должно быть больше 0,8. При пересечении факторов у нас нет чисел, которые отвечают критерию r2 >0,8, то мы выбираем критерии, которые оказывают наибольшее влияние. Т.к. у нас 18 степеней свободы, то мы можем выбрать только три фактора, значит у нас остается Х2, Х6, Х8(они оказывают наибольшее влияние). Построение эмпирических уровней регрессии 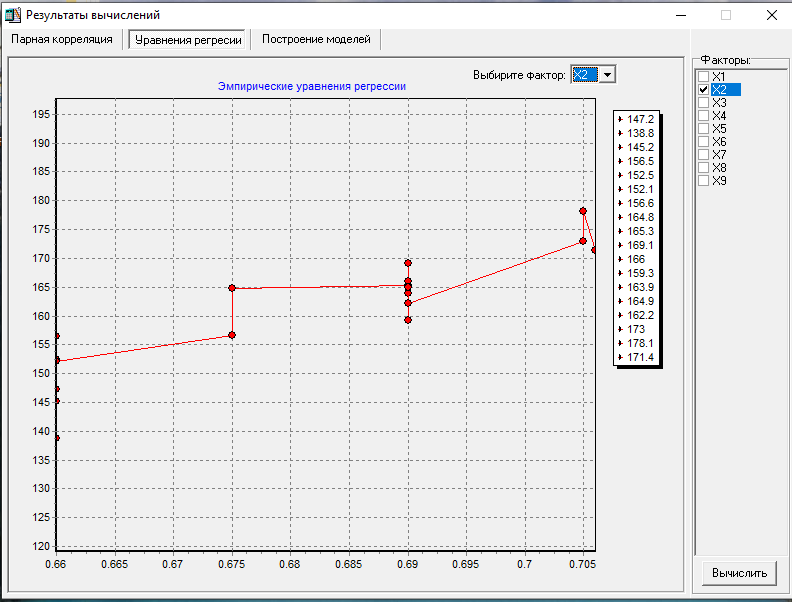 Рисунок 3: Эмп. уровень регрессии по факторному признаку Х1 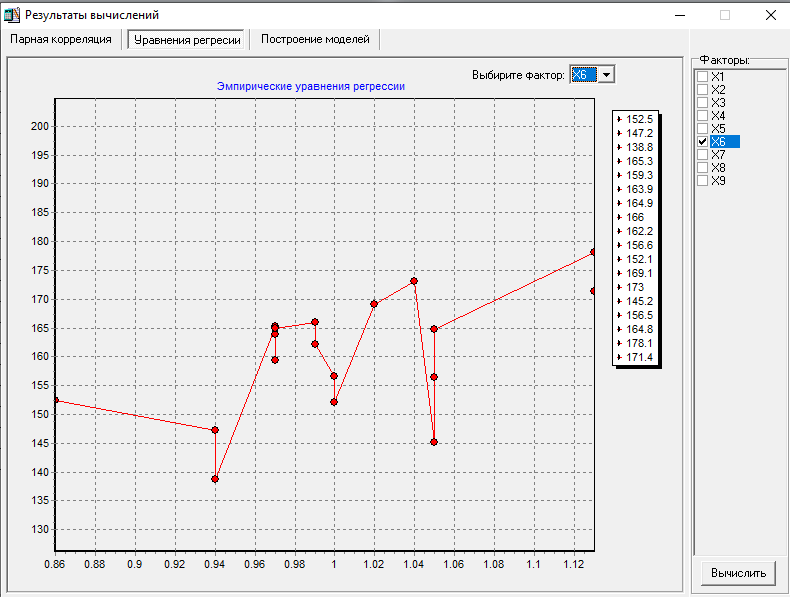 Рисунок 4: Эмп. уровень регрессии по факторному признаку Х6 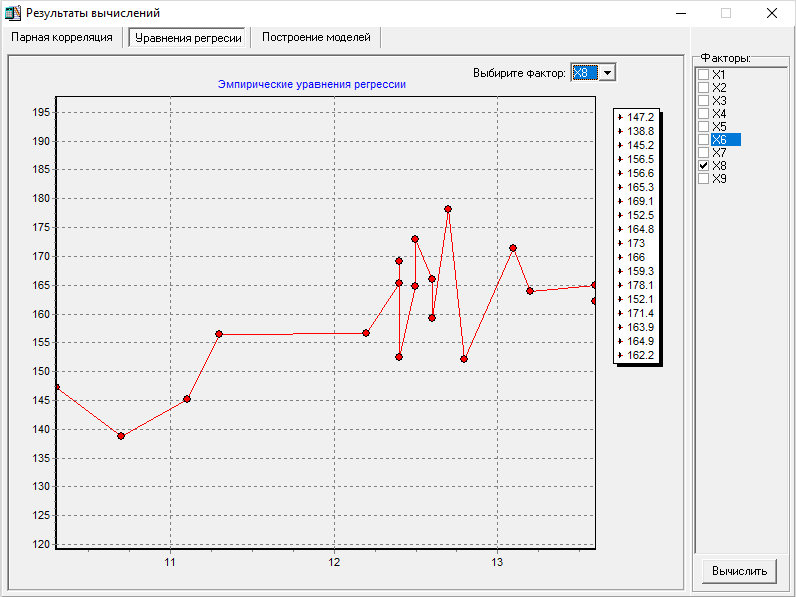 Рисунок 5: Эмп. уровень регрессии по факторному признаку Х8 5) Теоретические однофакторные модели 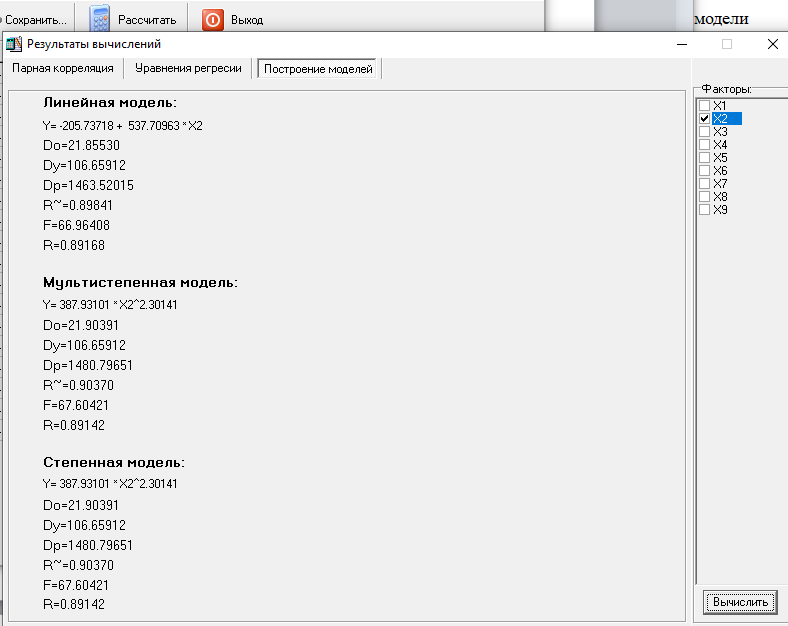 Рисунок 6: Фактор Х2 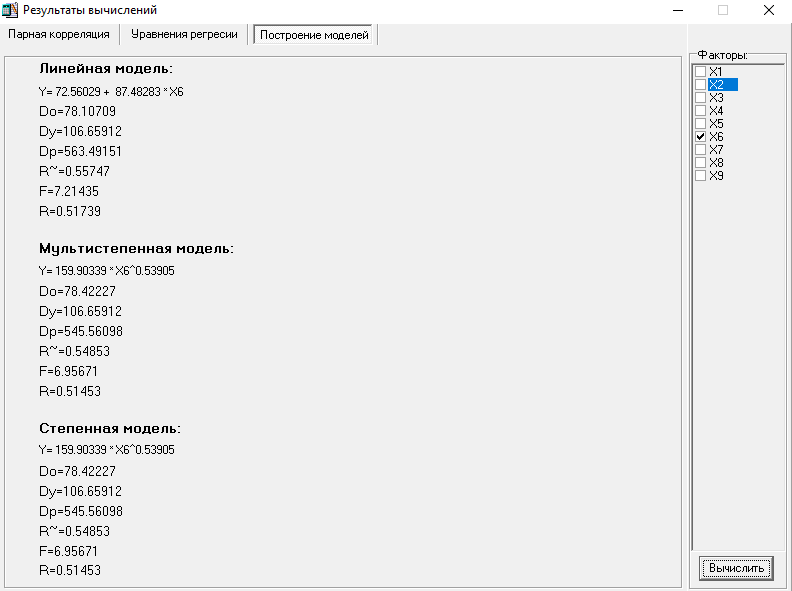 Рисунок 7: Фактор Х6 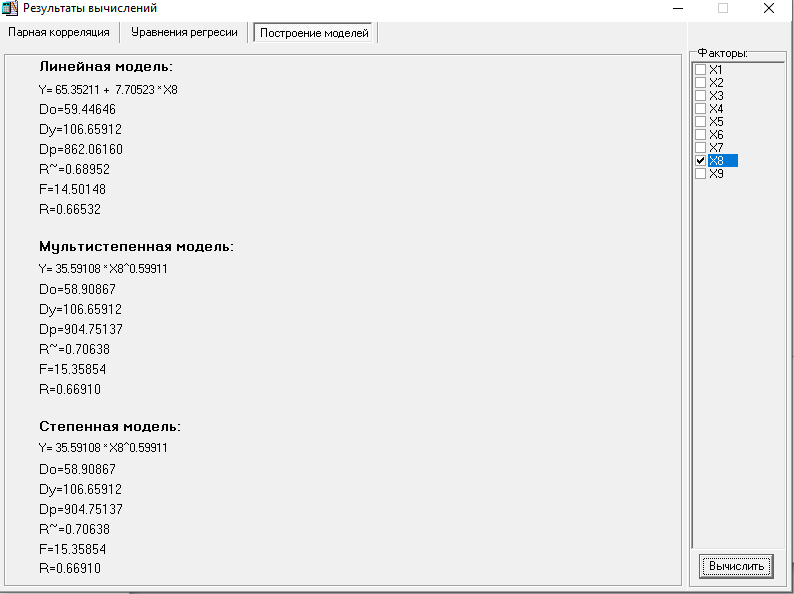 Рисунок 8: Фактор Х6 Произведем расчеты теоретических многофакторных моделей роста производительности труда: 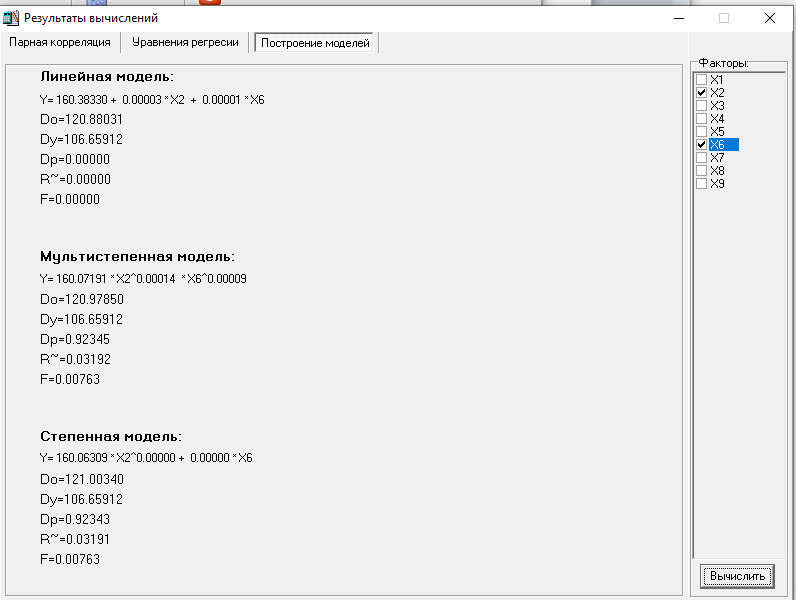 Рисунок 9: Факторы Х2 Х6 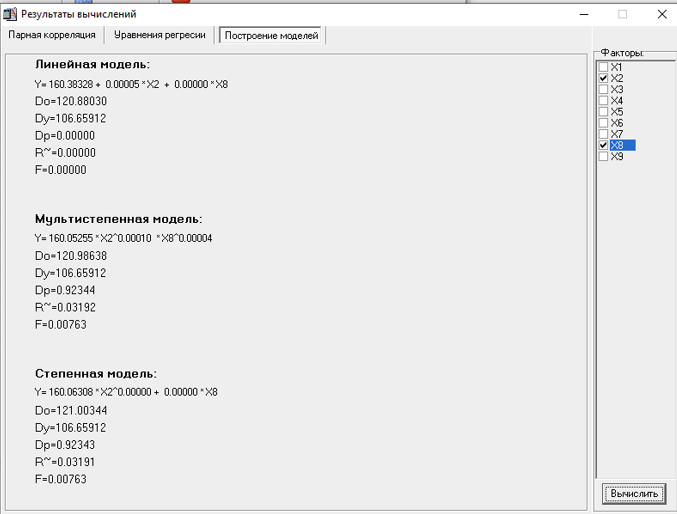 Рисунок 10: Факторы Х2 Х8 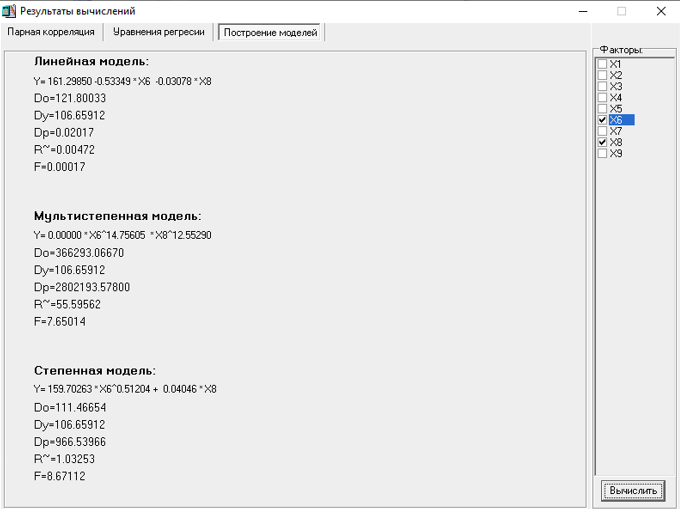 Рисунок 11: Факторы Х6 Х8 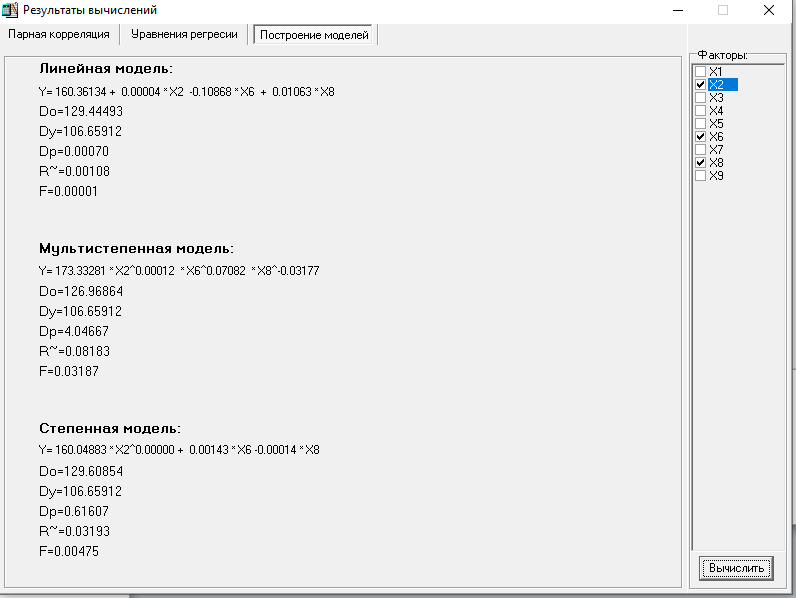 Рисунок 12: Факторы Х2 Х6 Х8 На основе полученных данных можно сделать вывод о том, что фактор Х2 (уровень технологии) обладает наибольшим влиянием (на результативный признак) на производительность труда, т.к.: 1)его коэффициент корреляции с результативным признаком самый высокий; 2)при сравнении с другими факторами (Х6 и Х8), Х2 имеет наименьшую остаточную дисперсию, которая определяется по остаточной дисперсии (D0) линейной модели. Исходя из этого, можно утверждать, что однофакторная модель на основе X2 является наилучшей моделью. Адекватность линейной модели проверяется по критерию Фишера. Вычисленное значение F линейной однофакторной модели каждого фактора сравнивается с табличным значением, которое в свою очередь находится благодаря степеням свободы (n, m-n-1), в нашем случае (1, 18-1-1) Fтабл= 4,49. Значение F линейной модели каждого нашего фактора больше Fтабл., как нам известно, Если F>Fтабл, то с вероятностью (1-0,95) можно считать, что результативный признак у линейно зависит от факторного признака Х2.
Вывод: Мы построили регрессионную модель производительности труда и произвели её анализ. |
