Задание 7. Дано комплексное число  . .
Записать число  в показательной, тригонометрической и алгебраической форме, изобразить его на комплексной плоскости. в показательной, тригонометрической и алгебраической форме, изобразить его на комплексной плоскости.
Записать в показательной, тригонометрической и алгебраической форме число 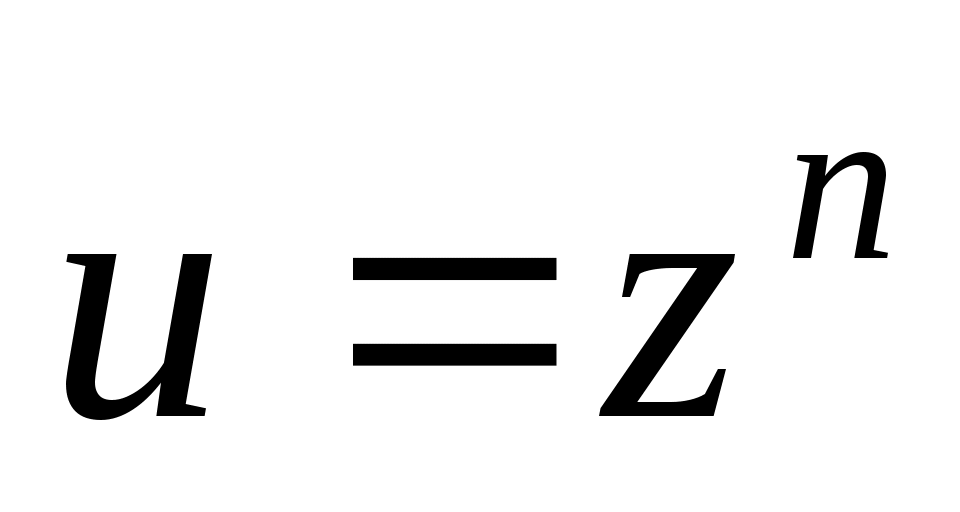 , где , где 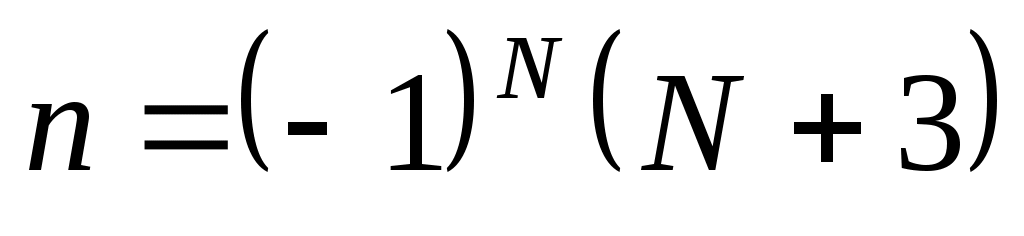 при при 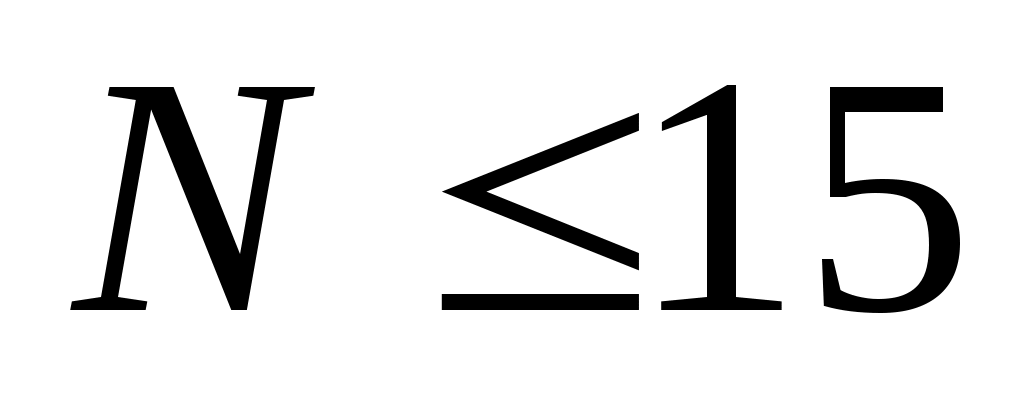 , и , и 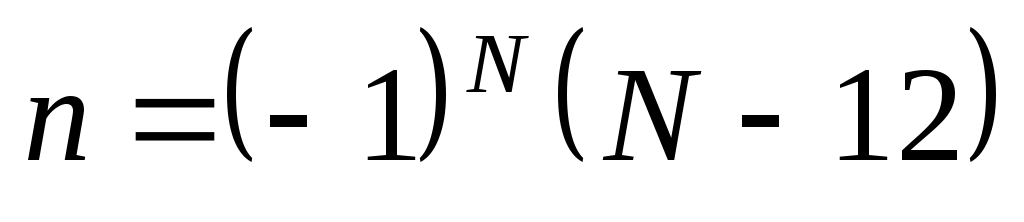 при при 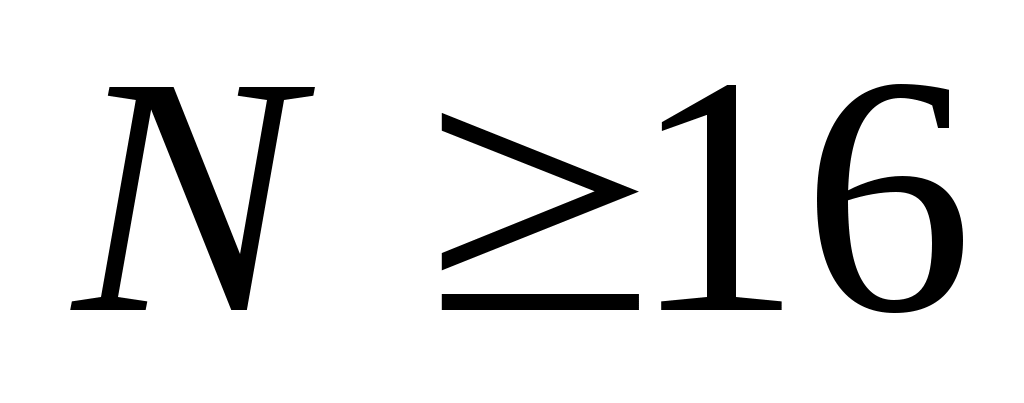 , ( , (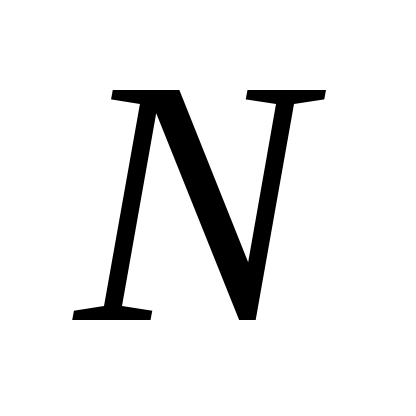 - номер варианта). - номер варианта).
Записать в показательной и тригонометрической форме каждое значение 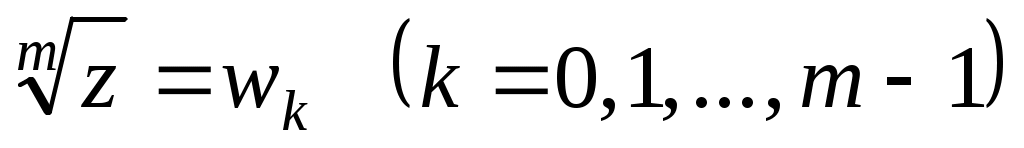 , где , где 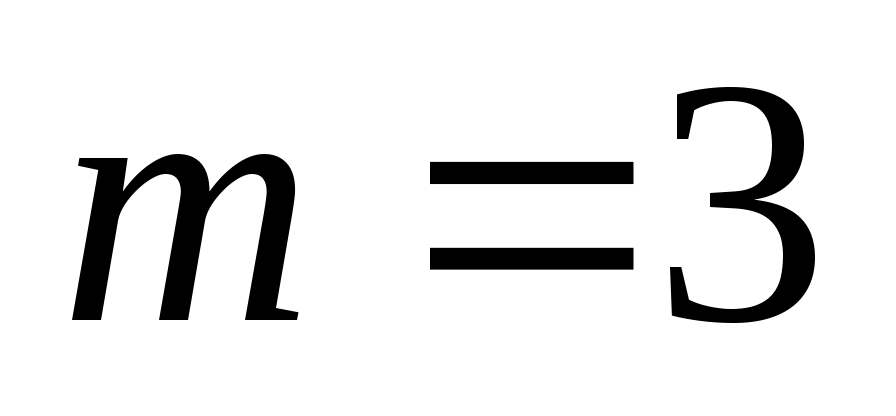 для нечетных вариантов и для нечетных вариантов и 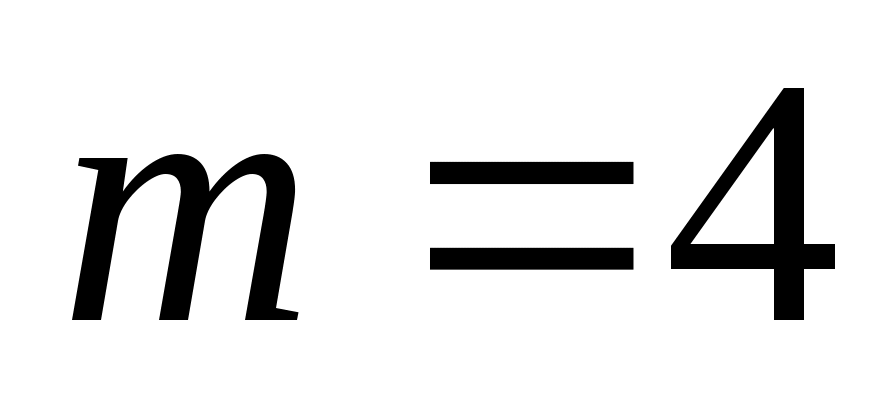 для четных вариантов. для четных вариантов.
Изобразить число  и числа и числа 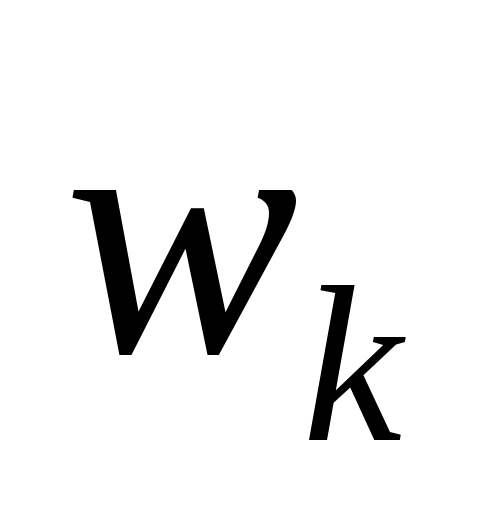 на одной комплексной плоскости. на одной комплексной плоскости.
№
|
|
№
|
|
№
|
|
1
|
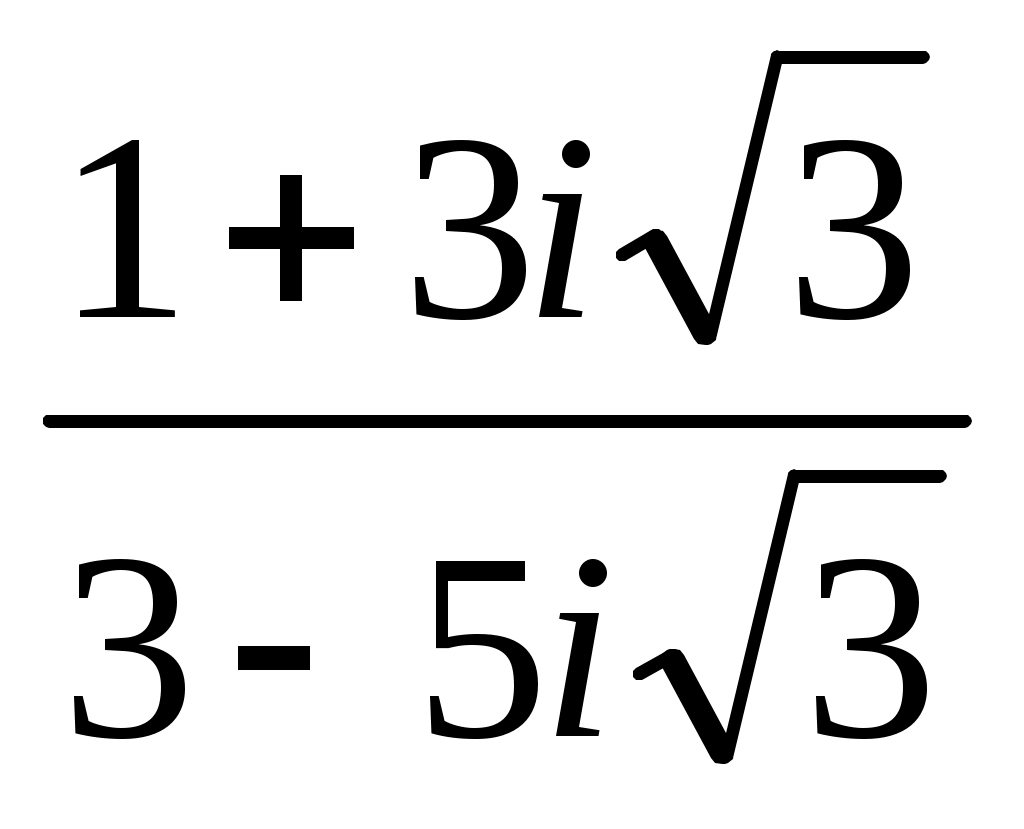
|
11
|
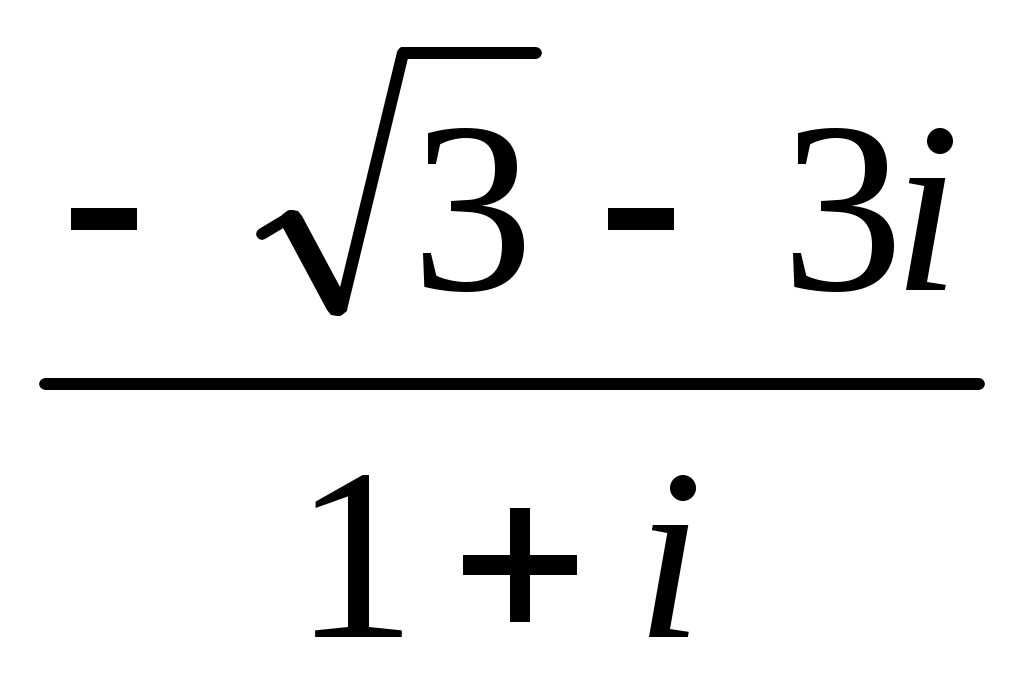
|
21
|
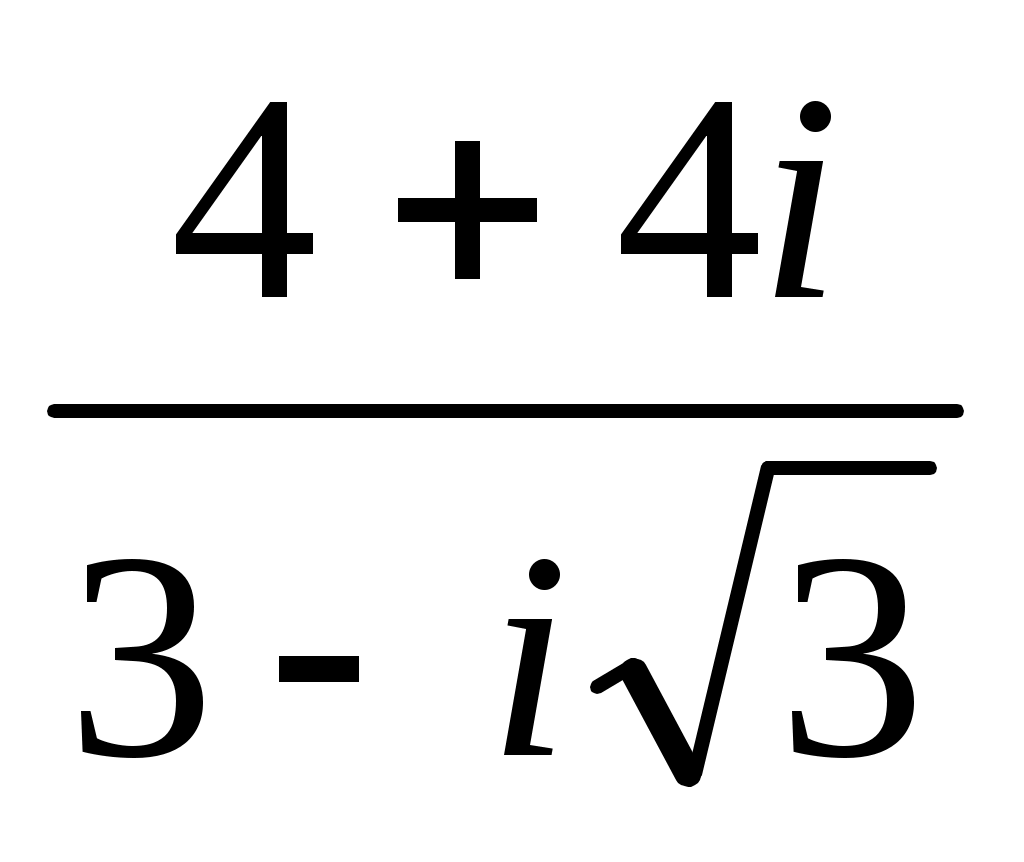
|
2
|
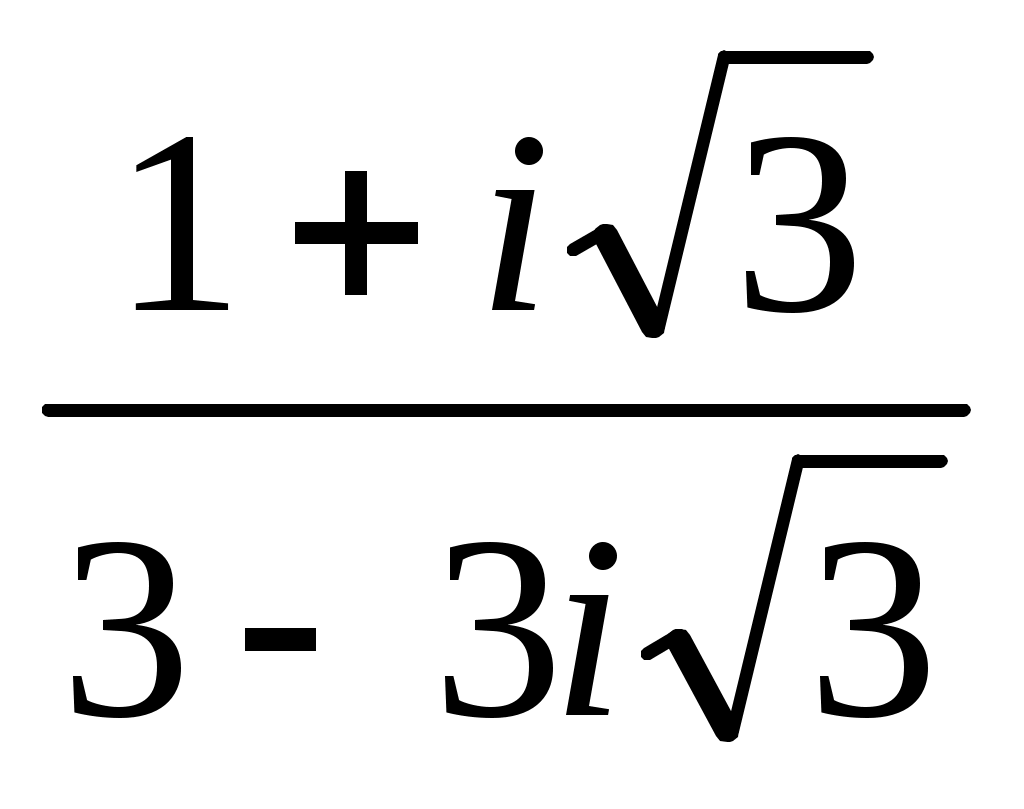
|
12
|
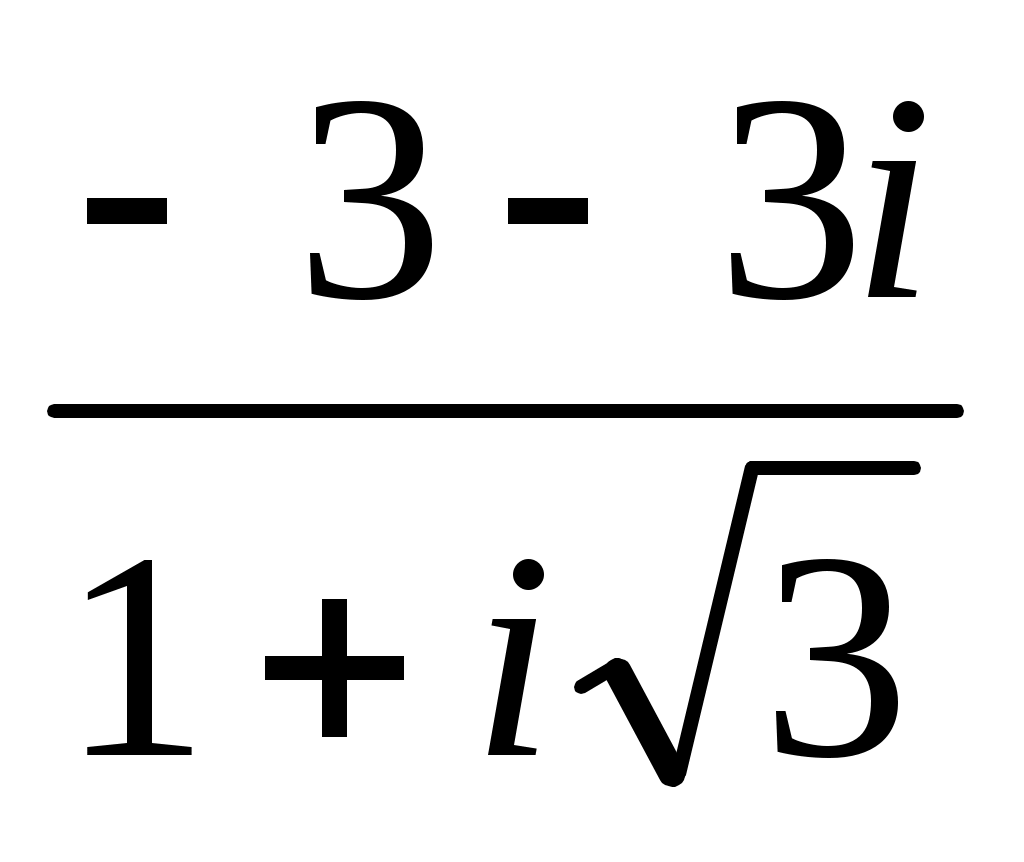
|
22
|
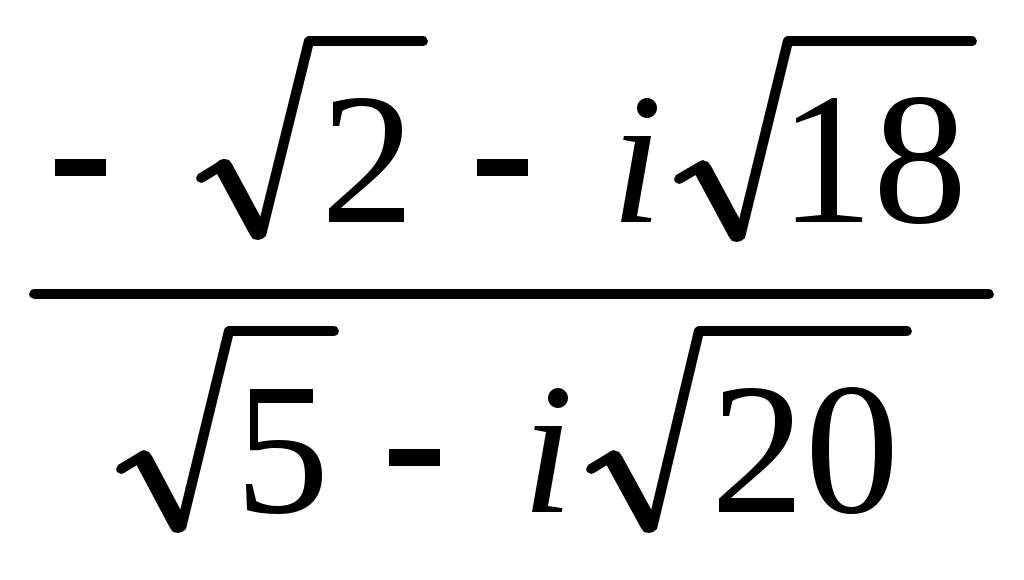
|
3
|
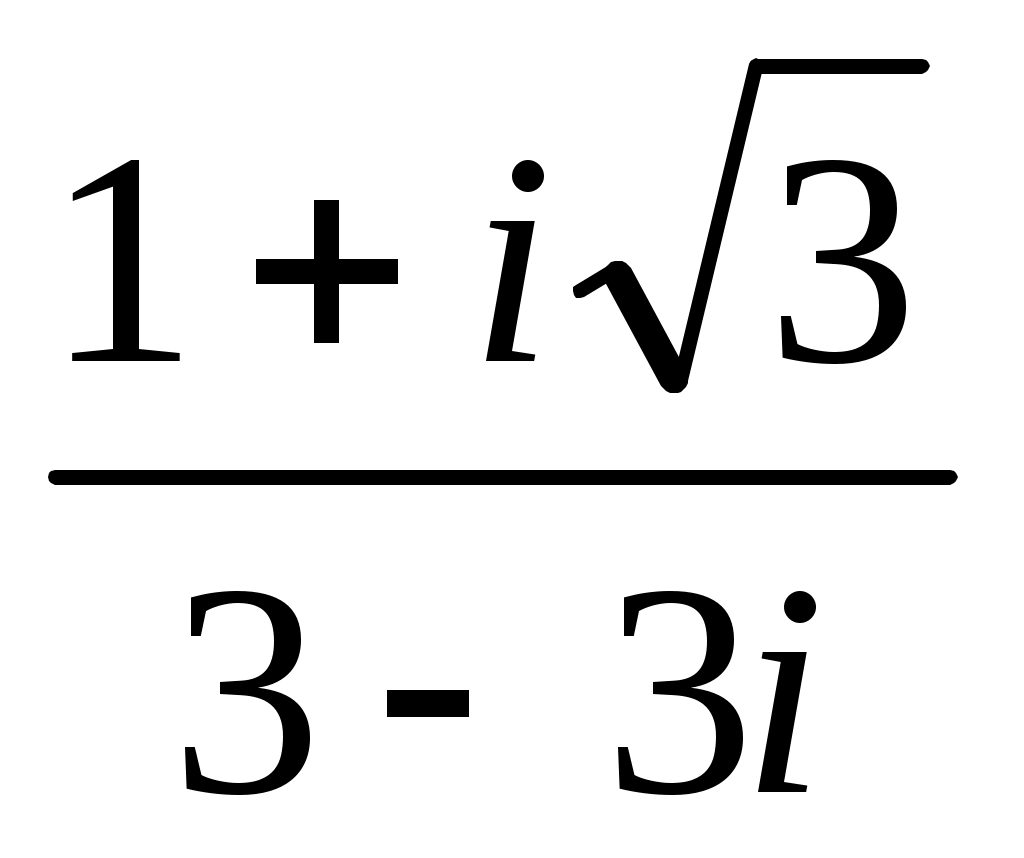
|
13
|
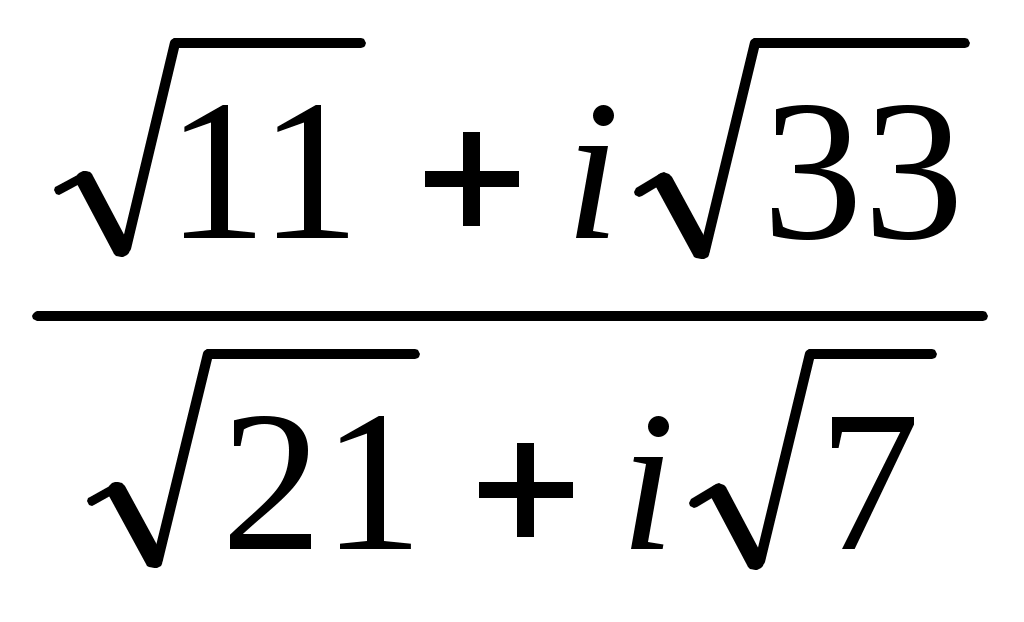
|
23
|
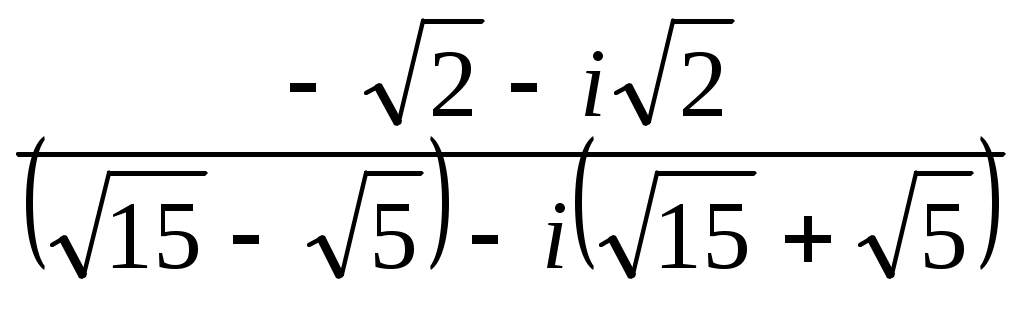
|
4
|
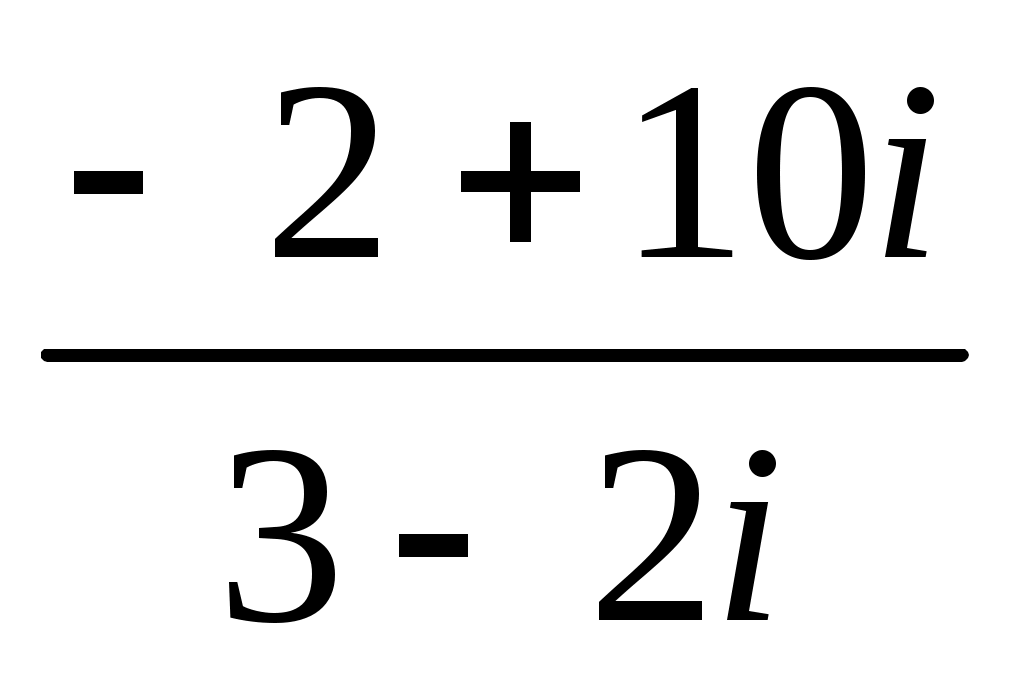
|
14
|
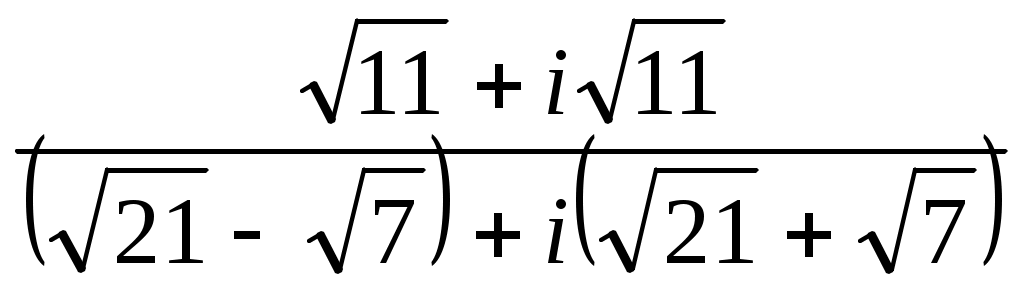
|
24
|
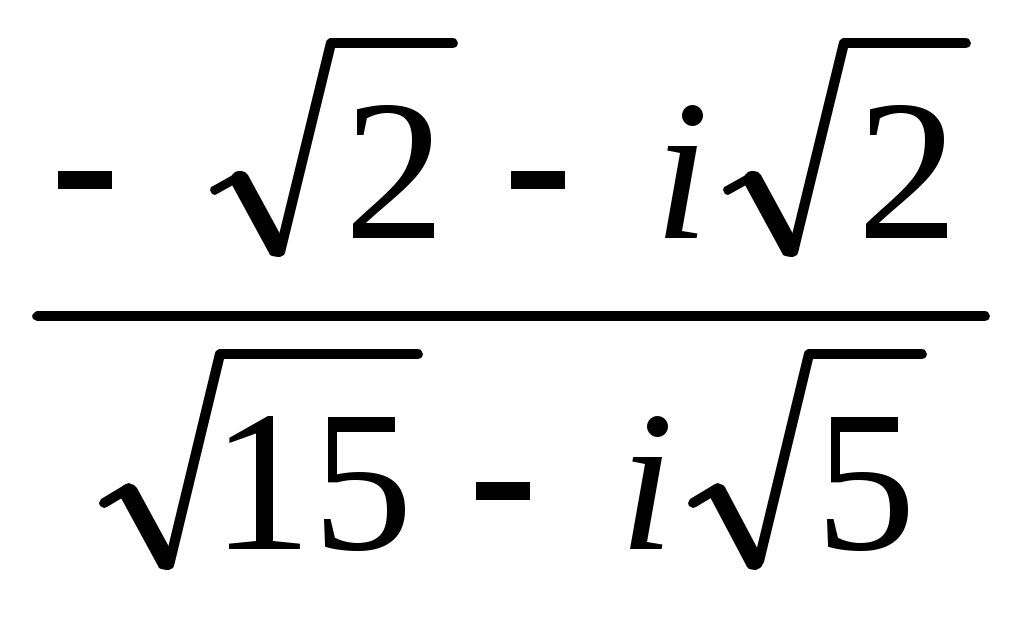
|
5
|
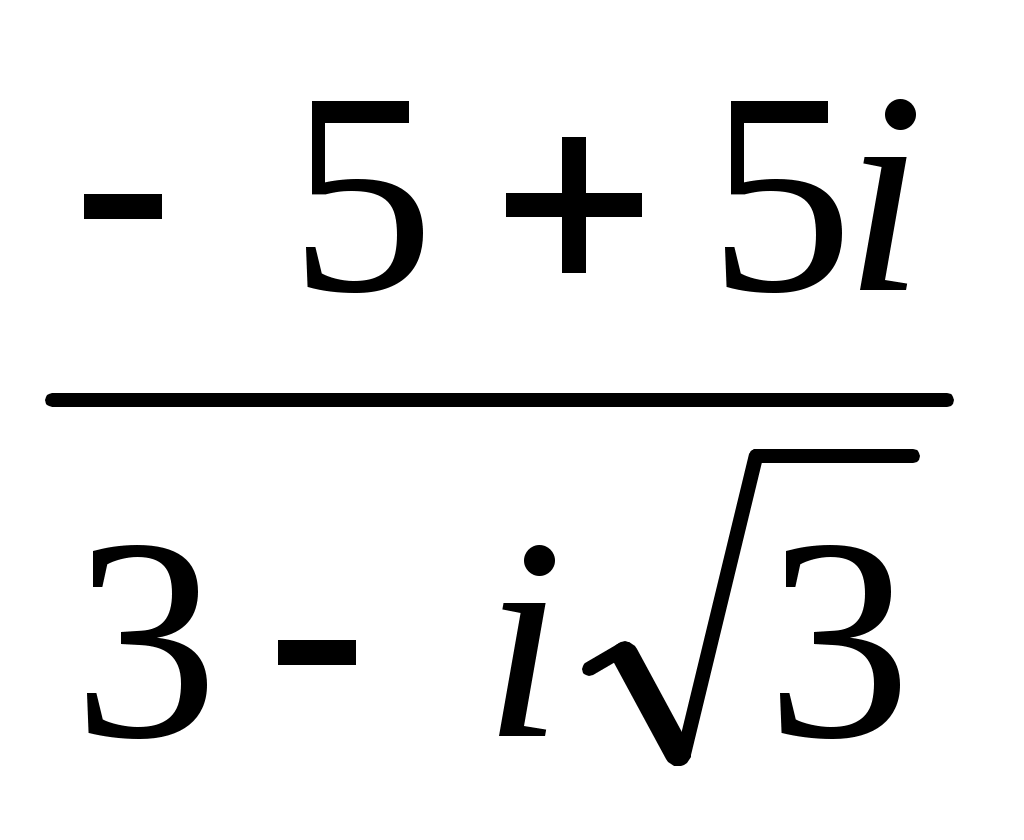
|
15
|
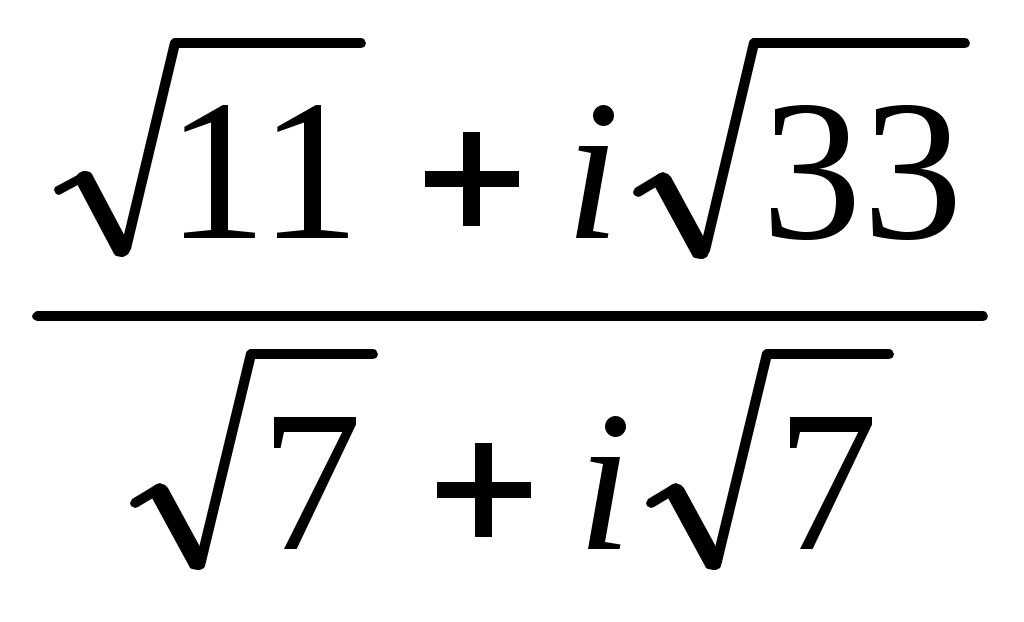
|
25
|
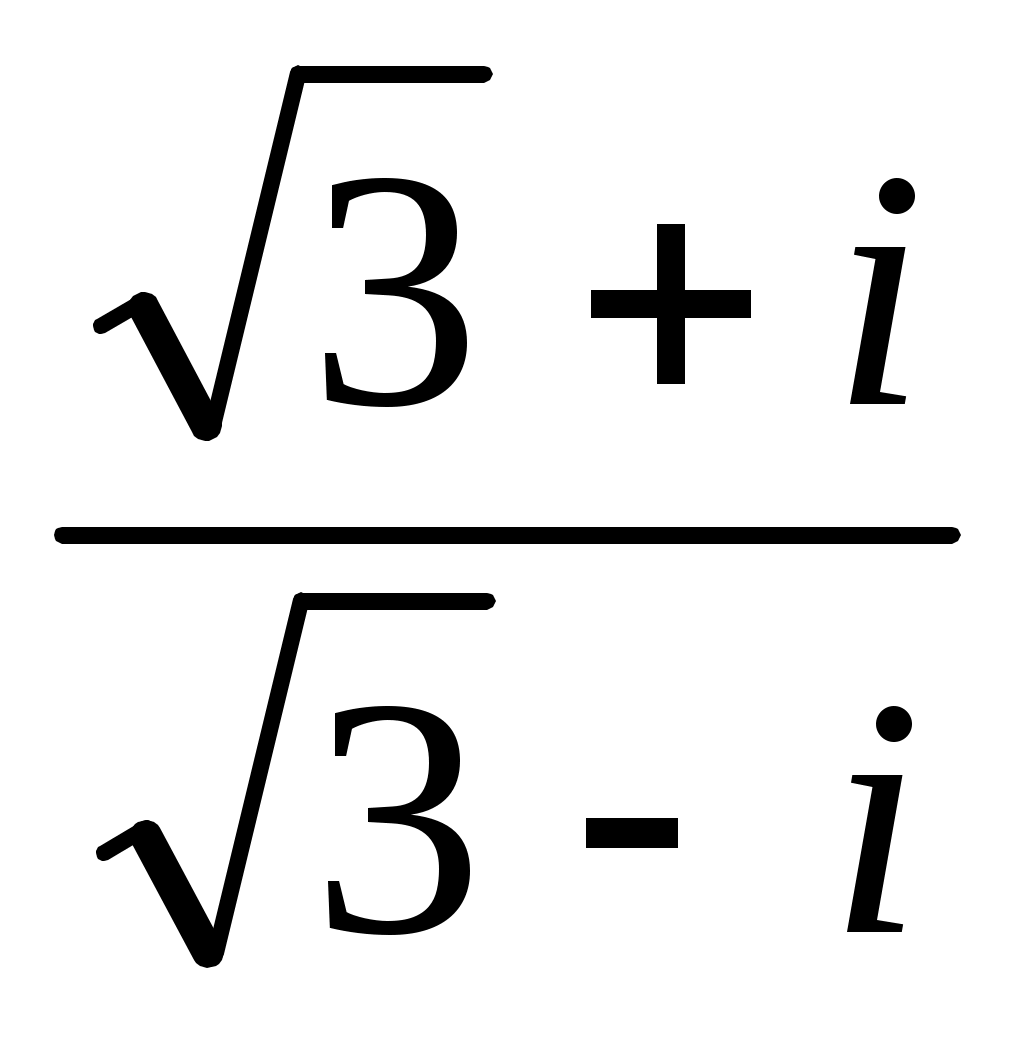
|
6
|
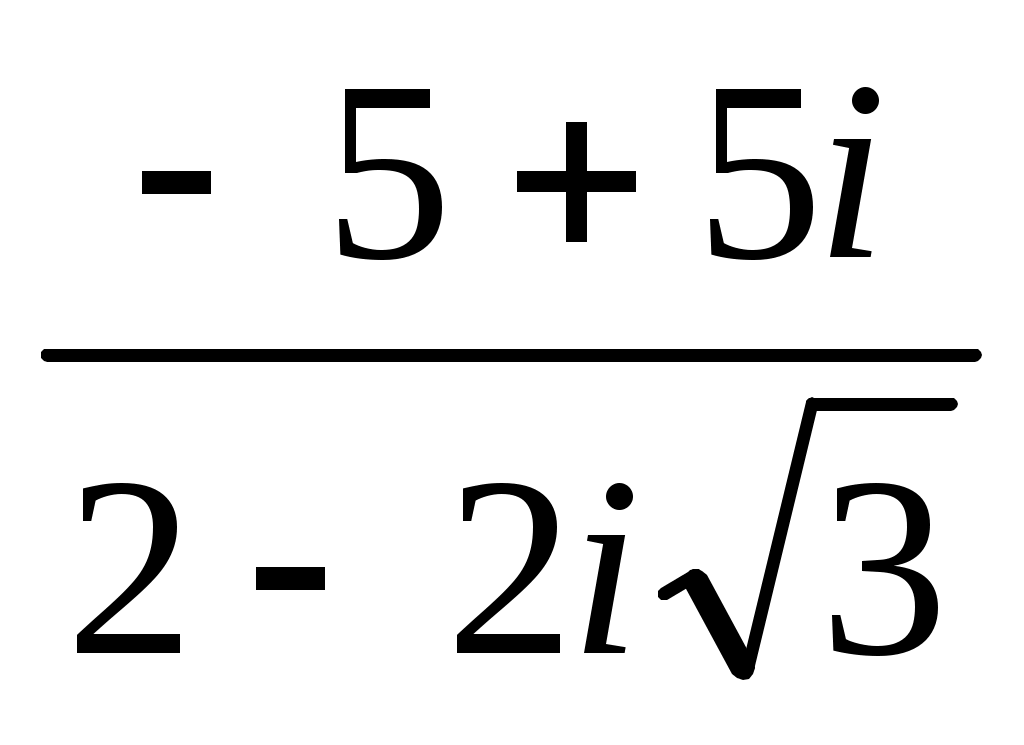
|
16
|
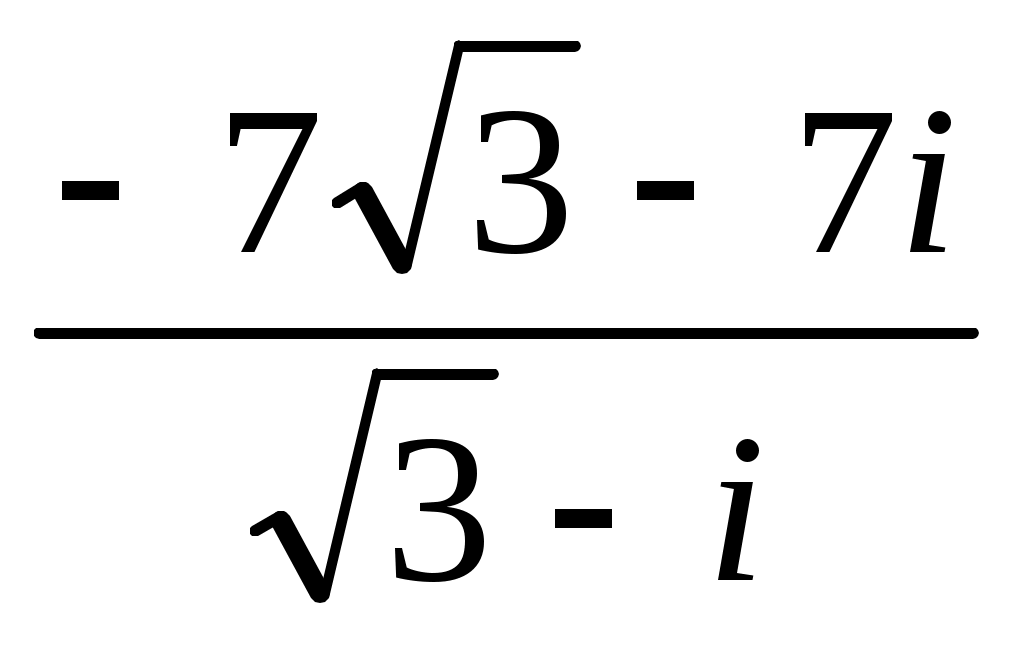
|
26
|
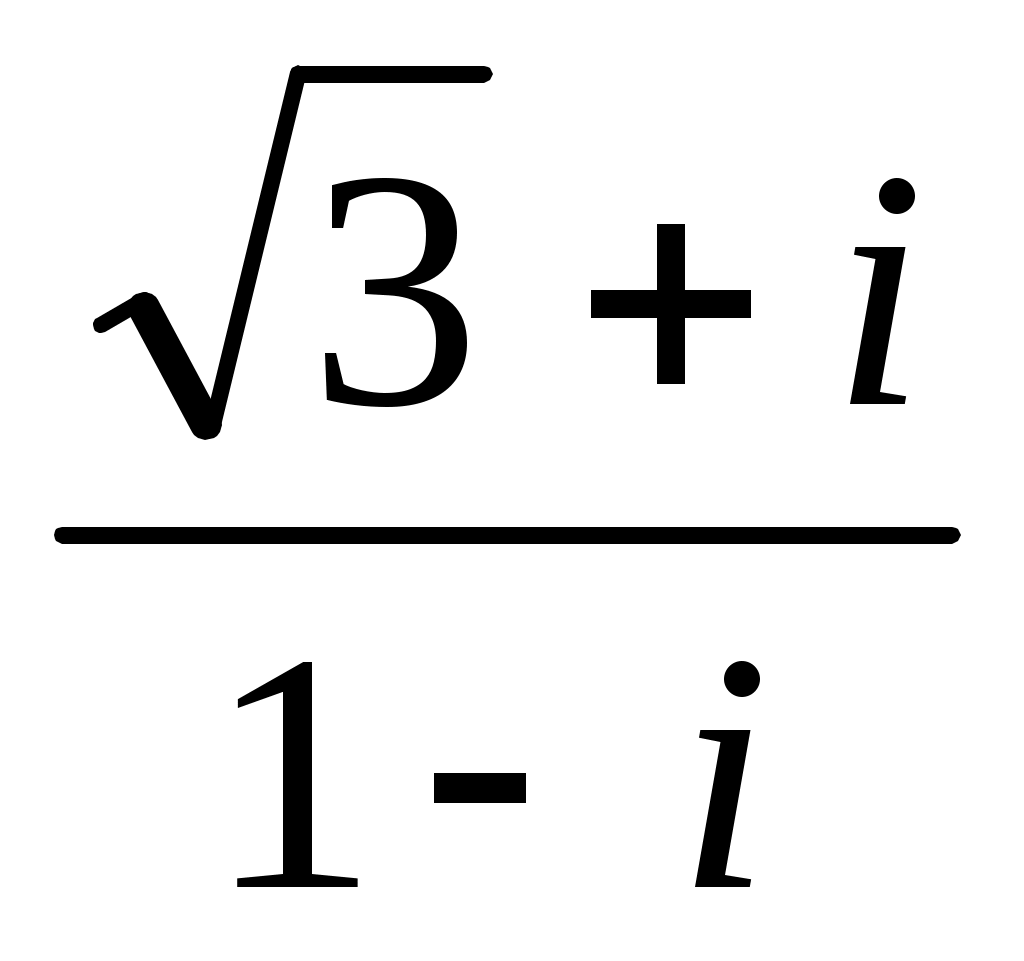
|
7
|
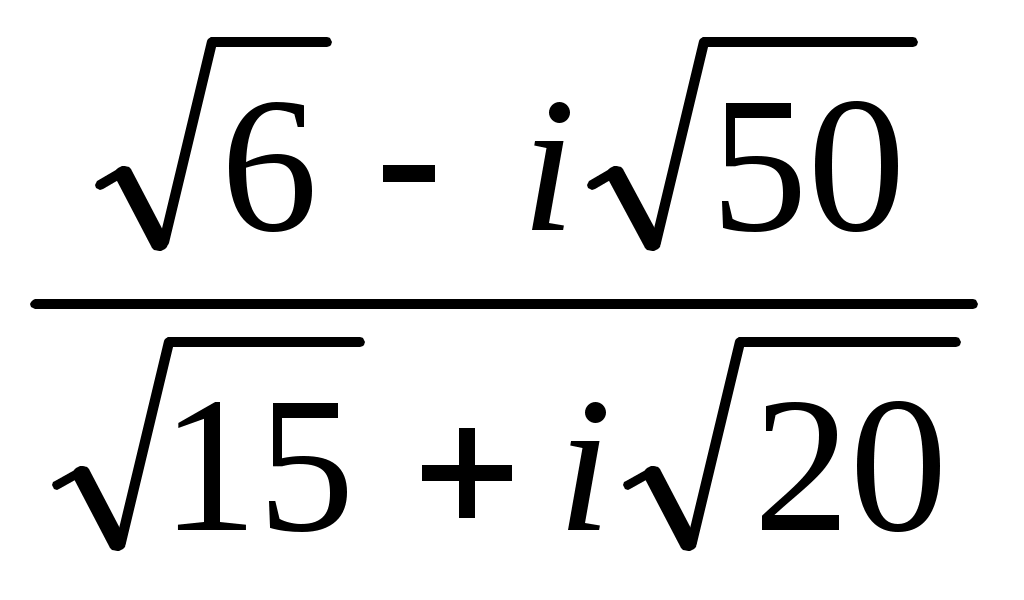
|
17
|
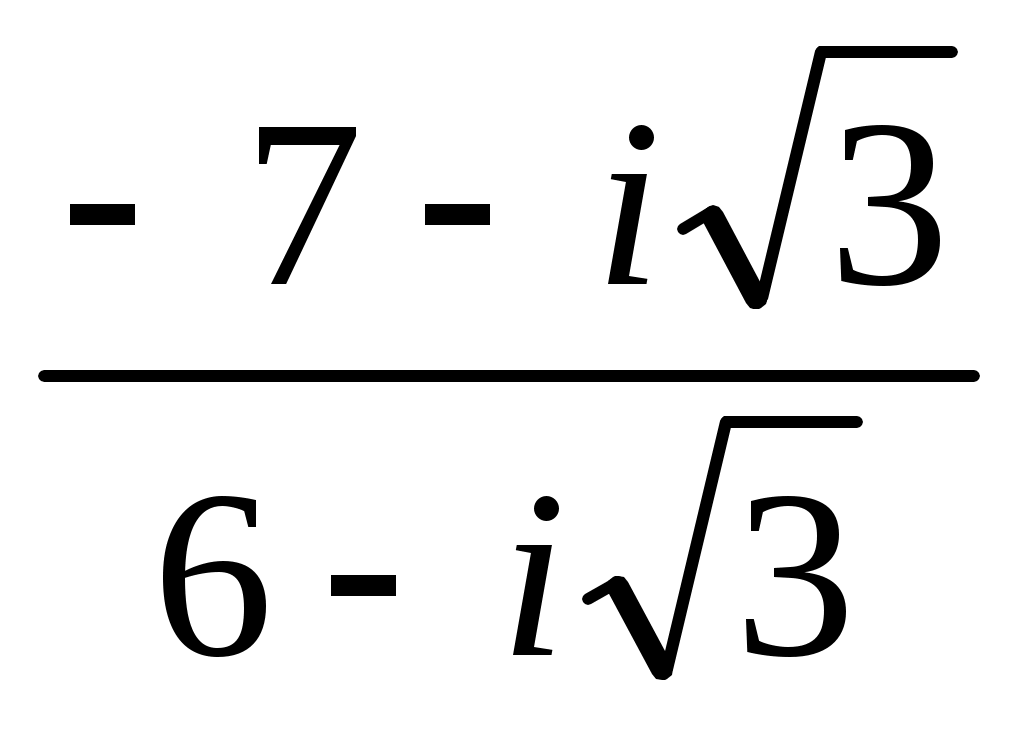
|
27
|
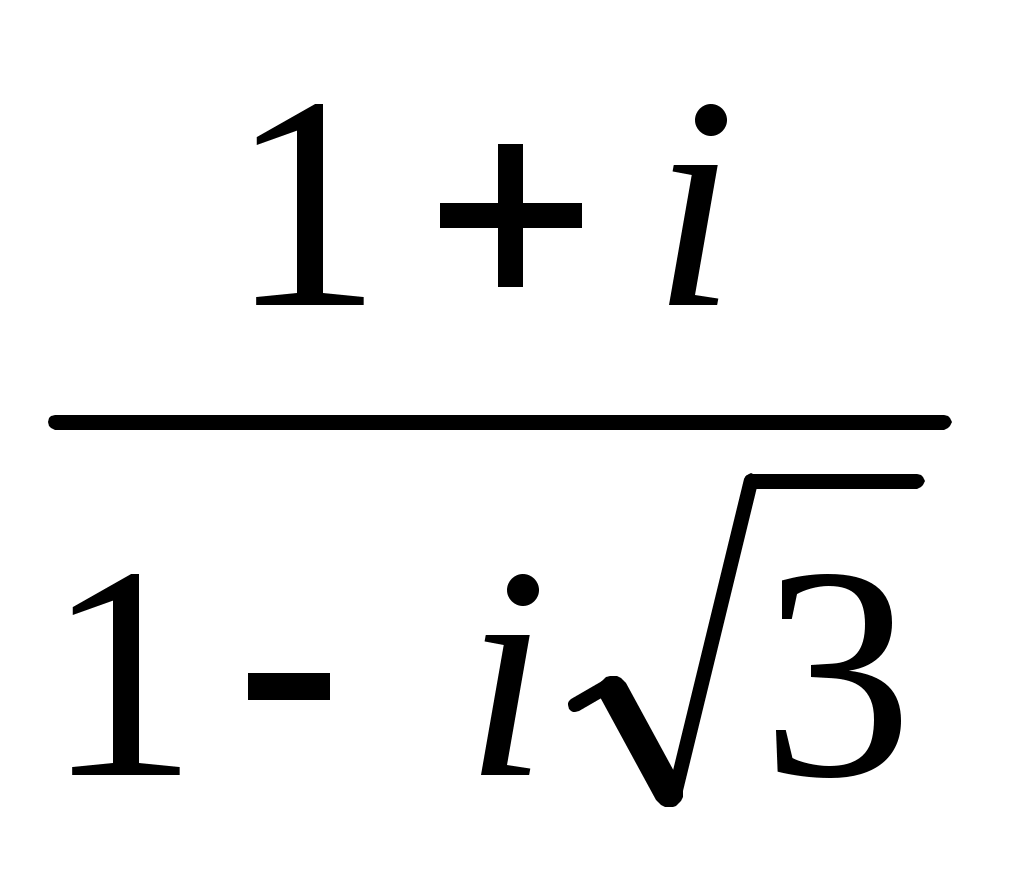
|
8
|
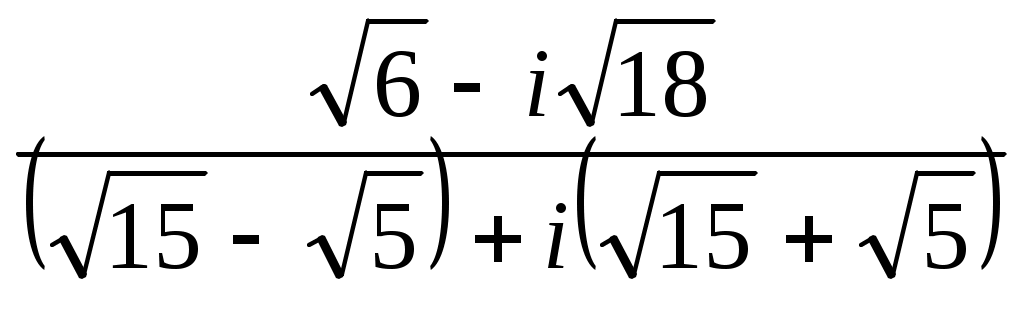
|
18
|
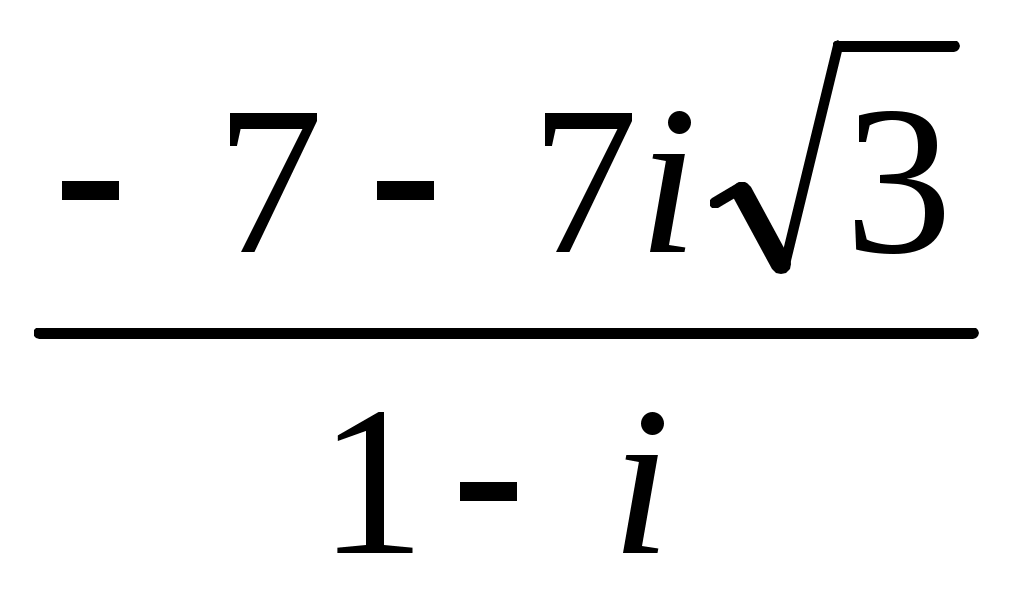
|
28
|
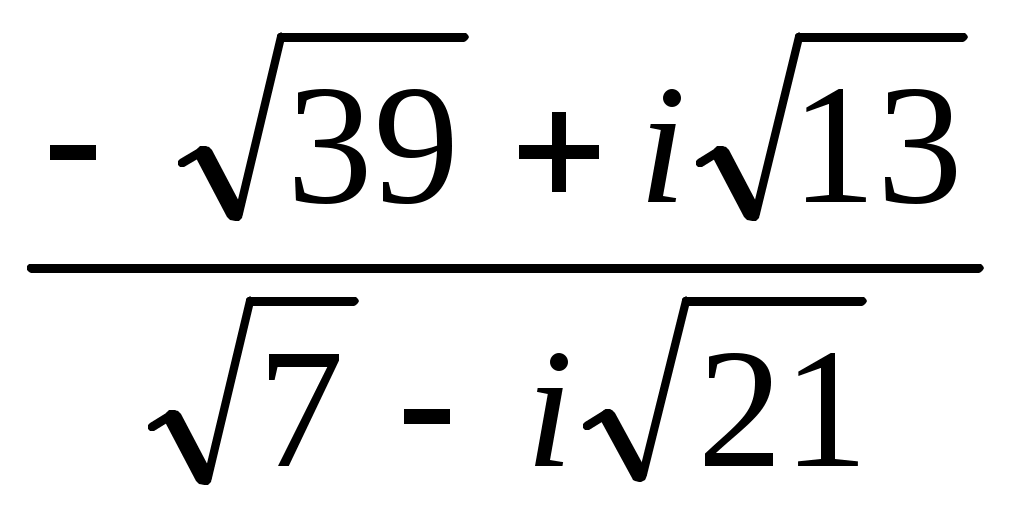
|
9
|
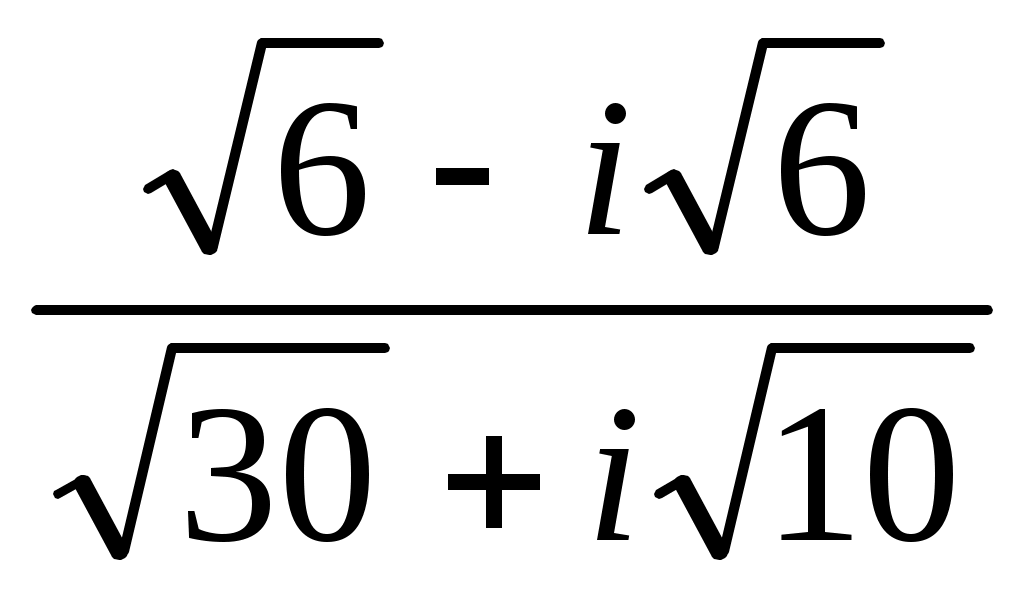
|
19
|
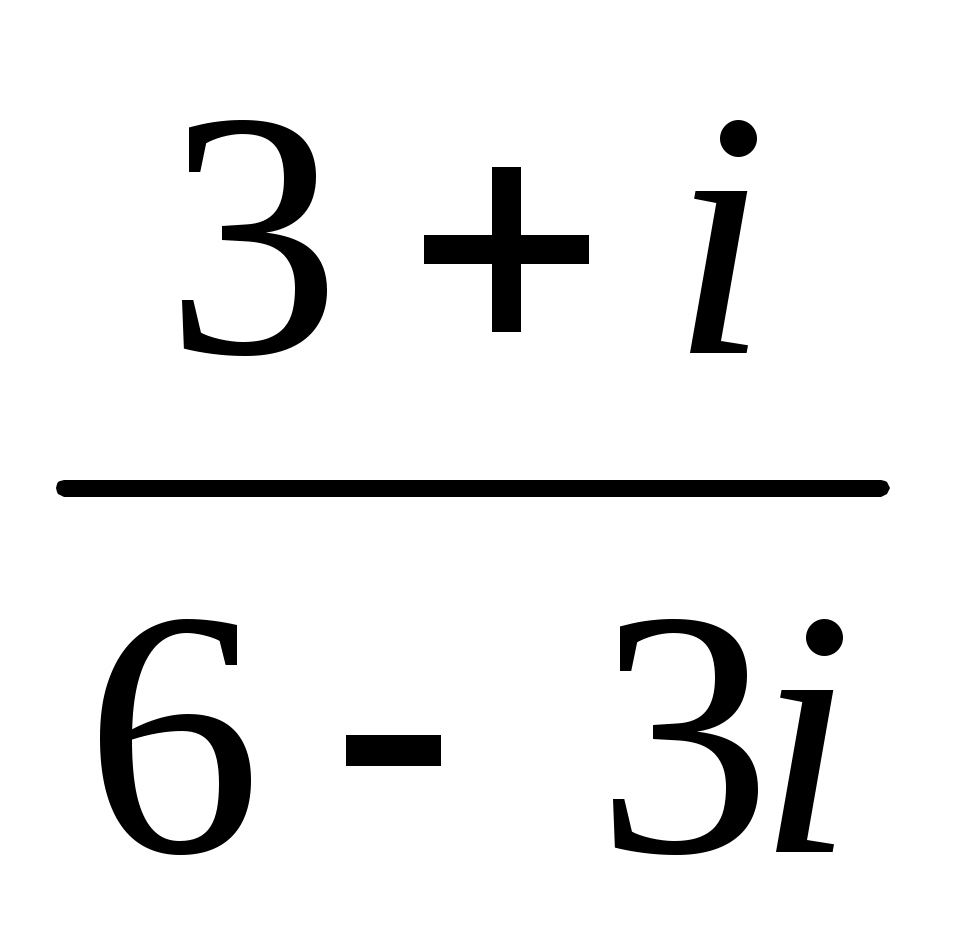
|
29
|
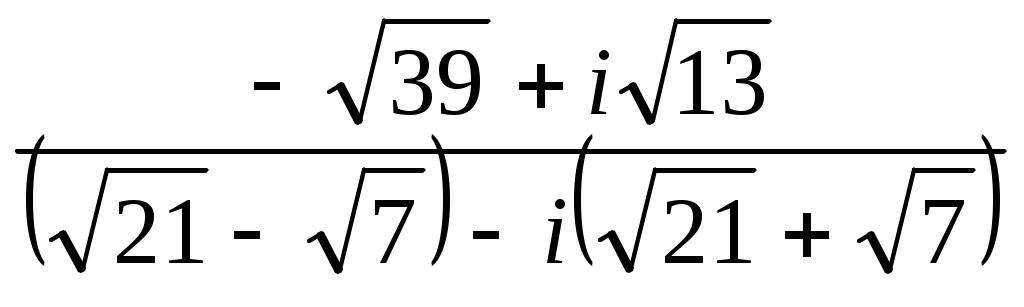
|
10
|
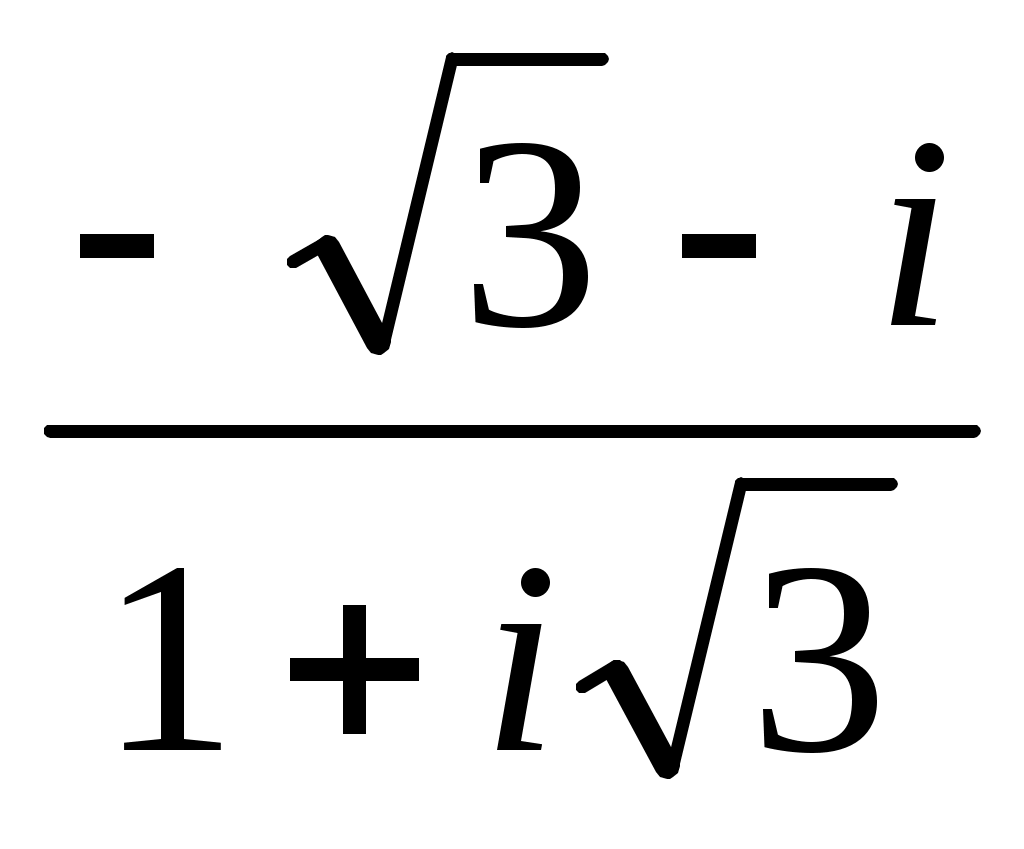
|
20
|
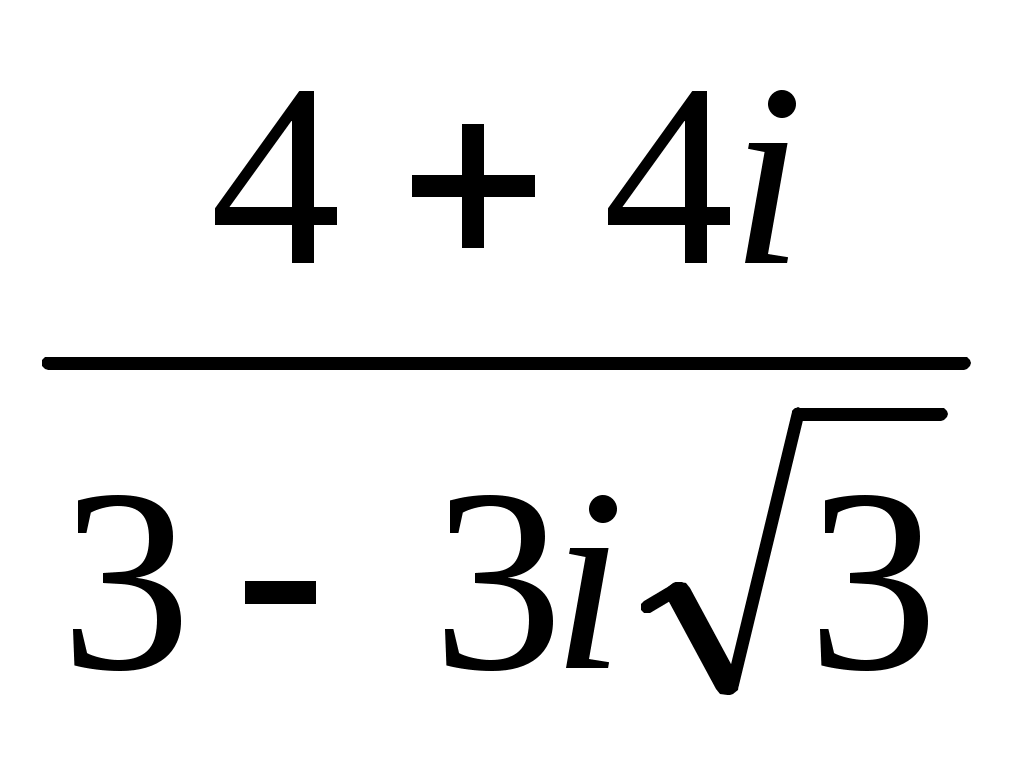
|
30
|
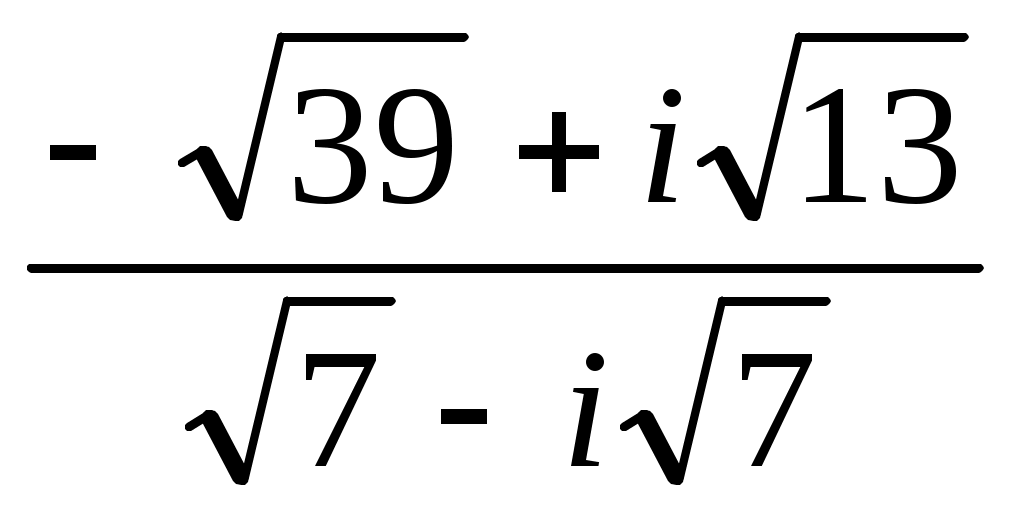
|
Задание 8. Дан многочлен 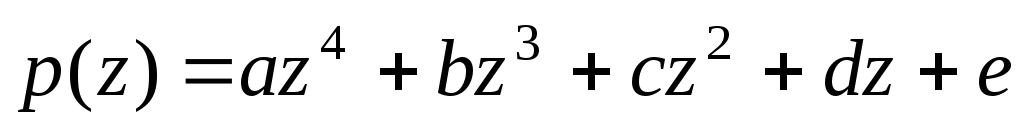 . .
Найти все корни многочлена 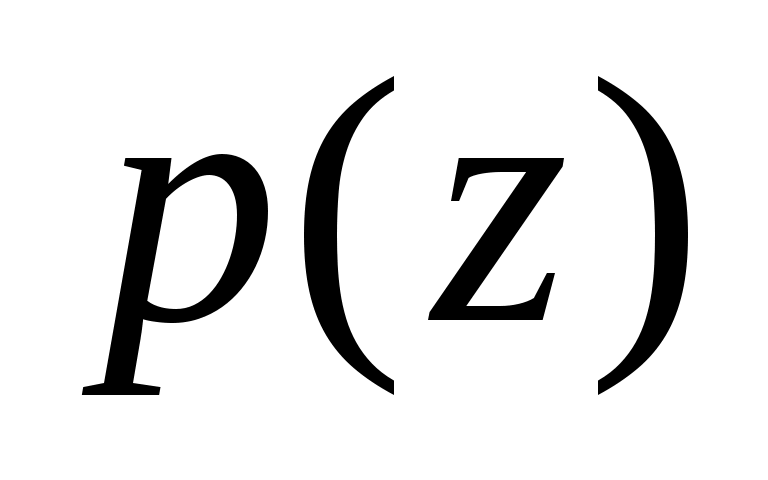 . Записать каждый корень в алгебраической форме, указать его кратность. . Записать каждый корень в алгебраической форме, указать его кратность.
Разложить многочлен 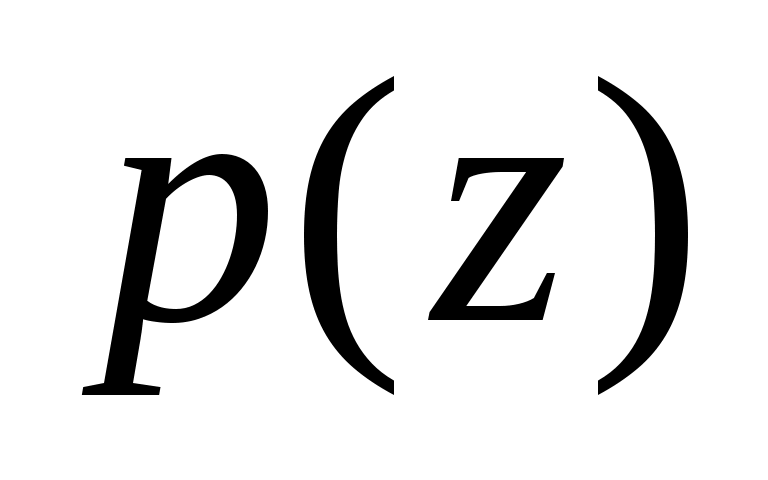 на неприводимые множители в множестве С комплексных чисел и в множестве R действительных чисел. на неприводимые множители в множестве С комплексных чисел и в множестве R действительных чисел.
№
|
a
|
b
|
c
|
d
|
e
|
№
|
a
|
b
|
c
|
d
|
e
|
1
|
3
|
1
|
7
|
5
|
2
|
16
|
1
|
–3
|
–8
|
–9
|
–5
|
2
|
1
|
3
|
1
|
0
|
4
|
17
|
1
|
1
|
–3
|
–4
|
–4
|
3
|
1
|
2
|
10
|
11
|
12
|
18
|
1
|
1
|
–2
|
–4
|
–8
|
4
|
2
|
11
|
13
|
3
|
9
|
19
|
1
|
2
|
–7
|
–18
|
–18
|
5
|
5
|
8
|
3
|
2
|
2
|
20
|
1
|
–3
|
–5
|
–21
|
–20
|
6
|
1
|
1
|
10
|
9
|
9
|
21
|
3
|
–1
|
5
|
3
|
2
|
7
|
4
|
20
|
41
|
40
|
16
|
22
|
1
|
2
|
7
|
6
|
5
|
8
|
4
|
4
|
5
|
2
|
1
|
23
|
1
|
3
|
8
|
8
|
8
|
9
|
5
|
2
|
22
|
8
|
8
|
24
|
1
|
1
|
10
|
9
|
9
|
10
|
3
|
5
|
6
|
3
|
1
|
25
|
1
|
–2
|
8
|
3
|
18
|
11
|
1
|
0
|
2
|
0
|
4
|
26
|
1
|
0
|
1
|
0
|
1
|
12
|
1
|
0
|
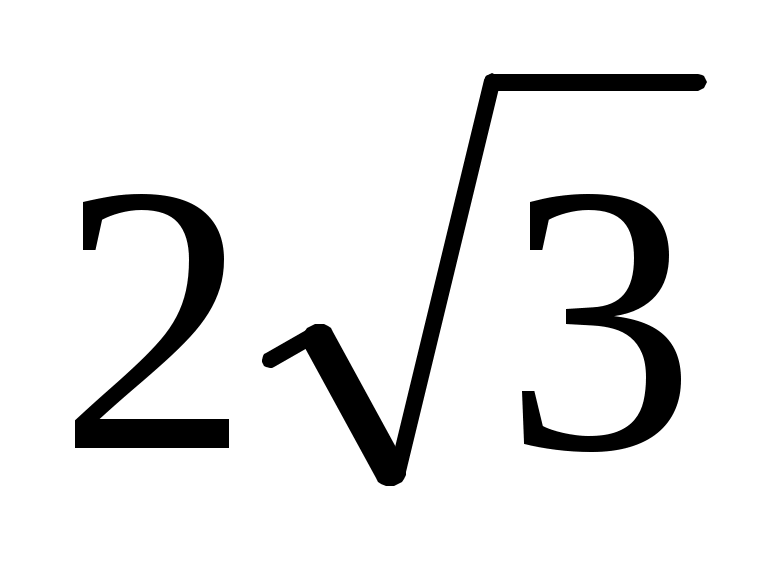
|
0
|
4
|
27
|
1
|
0
|
3
|
0
|
9
|
13
|
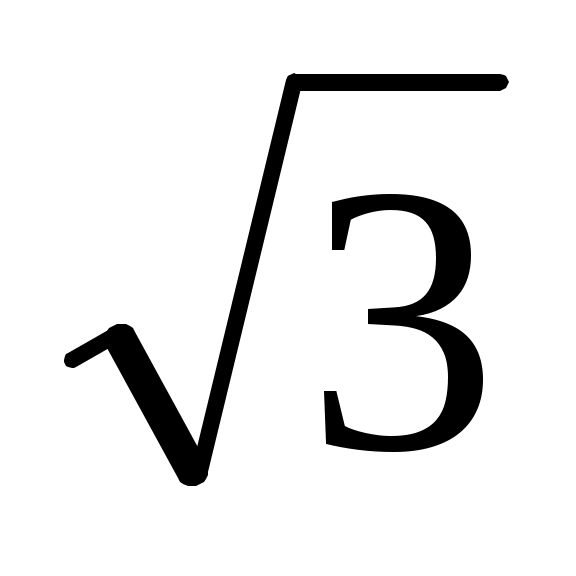
|
0
|
12
|
0
|
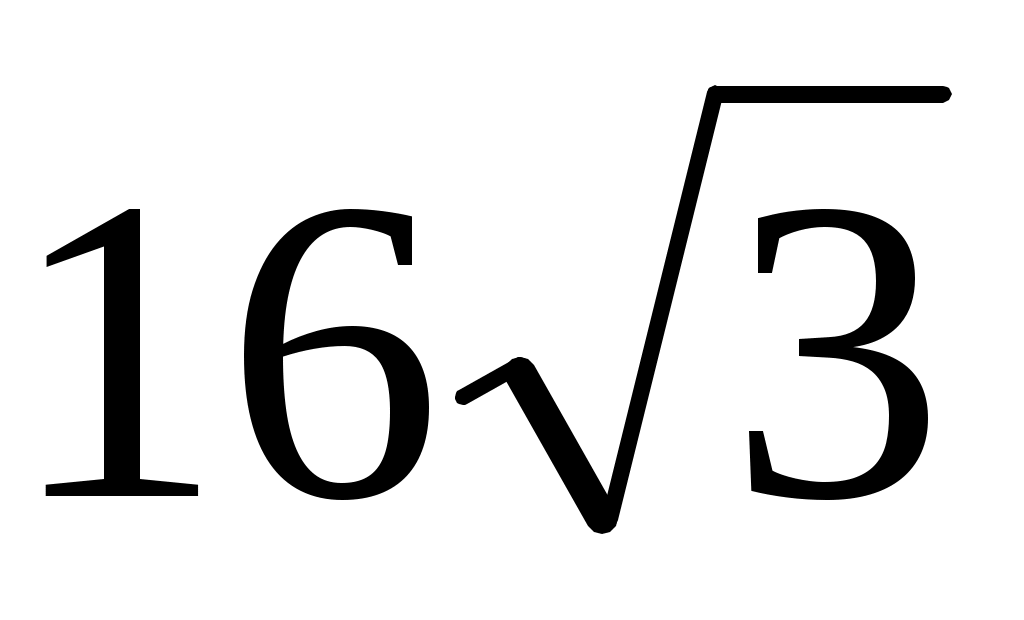
|
28
|
1
|
0
|
–1
|
0
|
1
|
14
|
1
|
0
|
2
|
0
|
2
|
29
|
1
|
0
|
–9
|
0
|
81
|
15
|
1
|
0
|
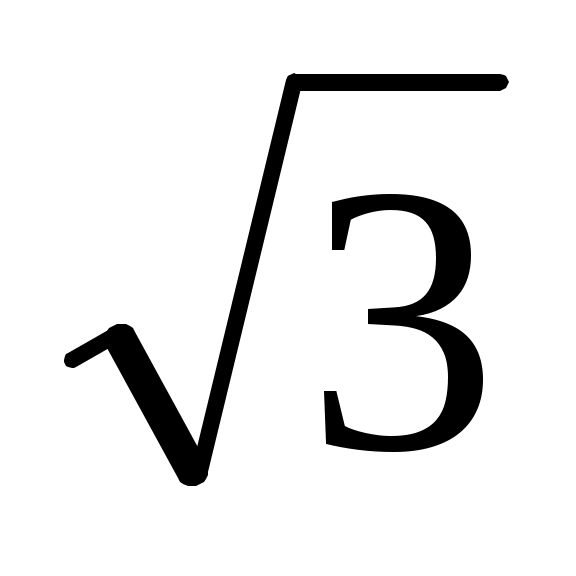
|
0
|
1
|
30
|
1
|
0
|
4
|
0
|
16
|
Указания: 1) в вариантах 15, 1620 найти целочисленные корни многочлена; 2) в вариантах 610, 2125 известен корень z0:
Задание 9. Даны векторы 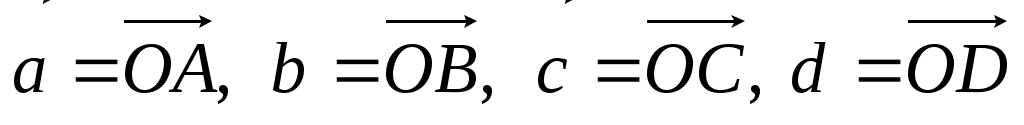 . Лучи . Лучи 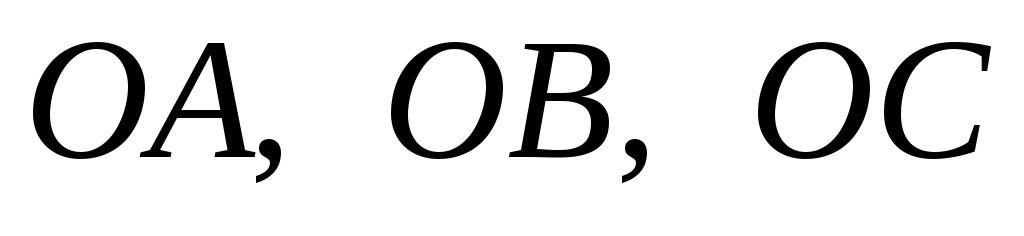 являются ребрами трехгранного угла являются ребрами трехгранного угла 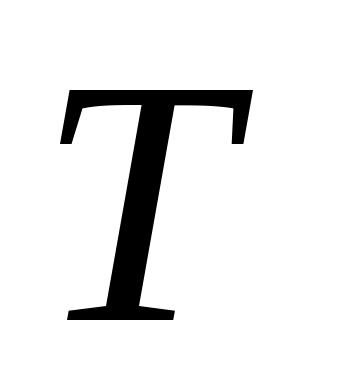 . .
Доказать, что векторы 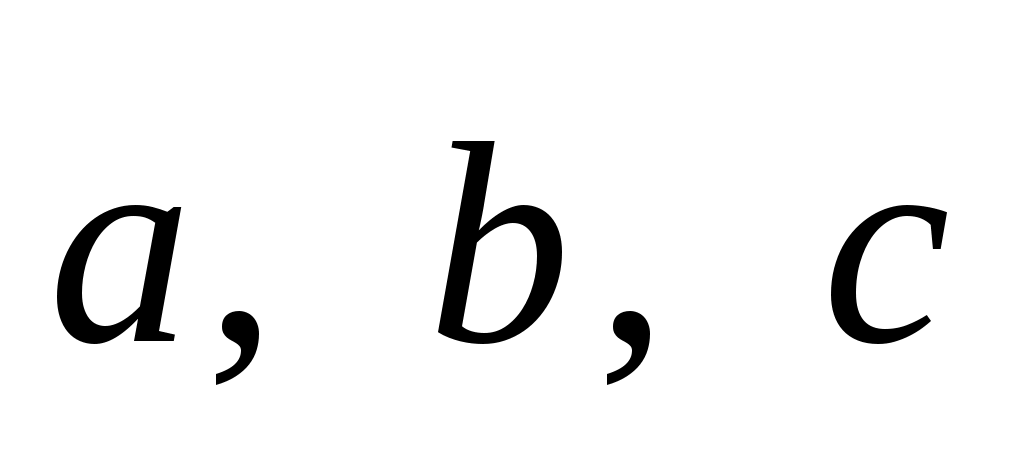 линейно независимы. линейно независимы.
Разложить вектор 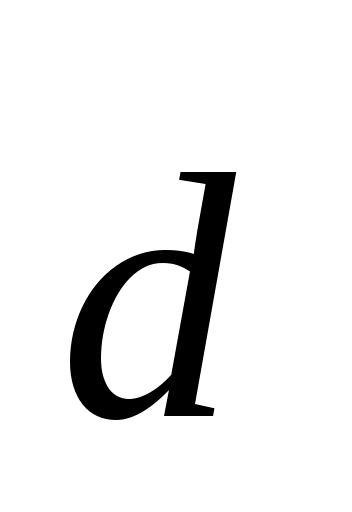 векторам векторам 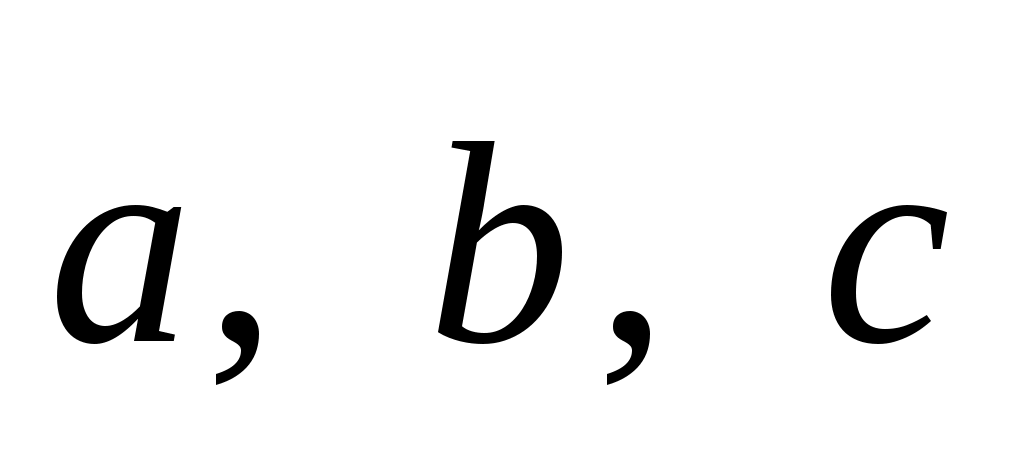 (возникающую в процессе решения систему уравнений решить с помощью обратной матрицы). (возникающую в процессе решения систему уравнений решить с помощью обратной матрицы).
Определить, лежит ли точка 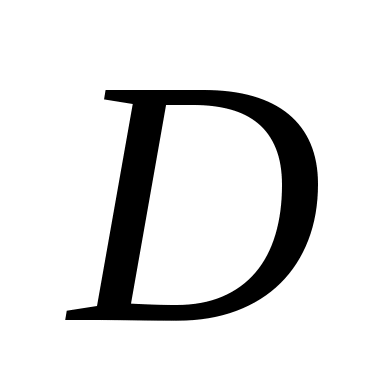 внутри угла внутри угла 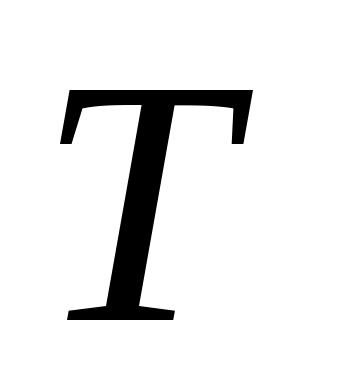 , вне , вне 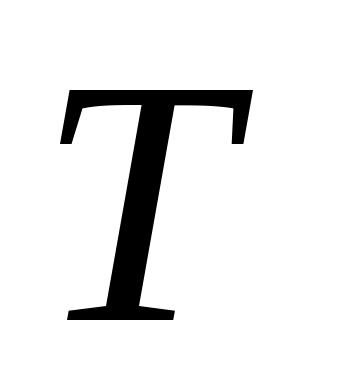 , на одной из границ , на одной из границ 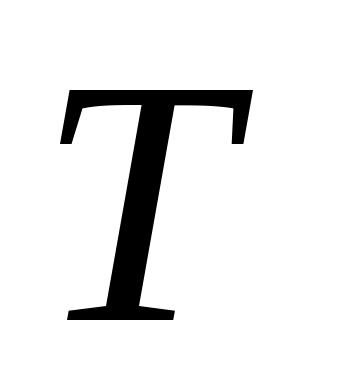 (какой, т.е. указать на какие из векторов (какой, т.е. указать на какие из векторов 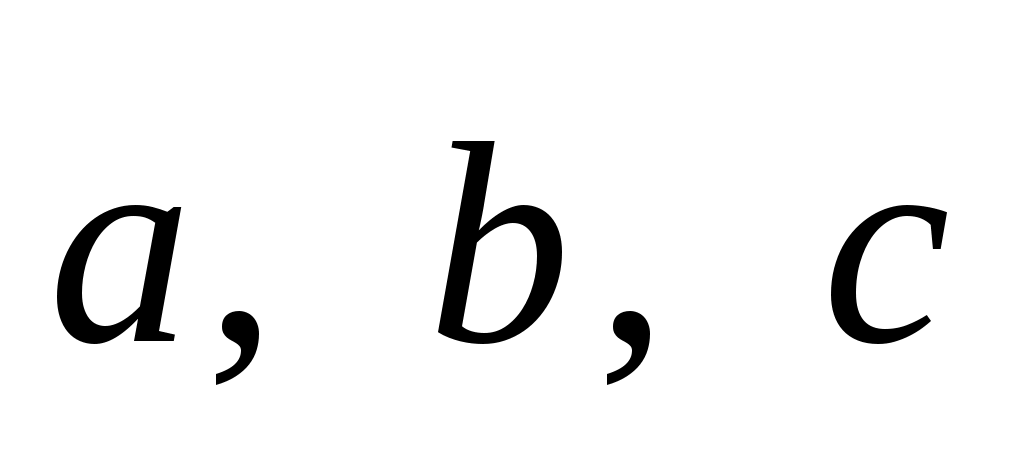 натянута эта граница). натянута эта граница).
Определить, при каких значениях действительного параметра 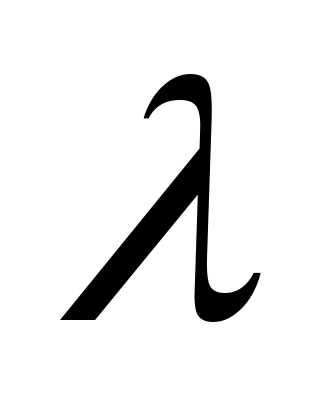 вектор вектор 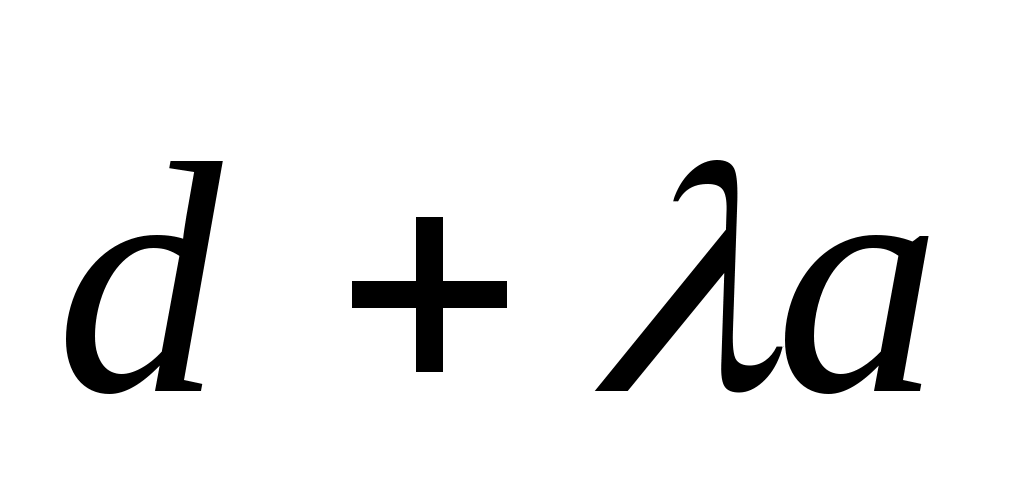 , отложенный от точки , отложенный от точки 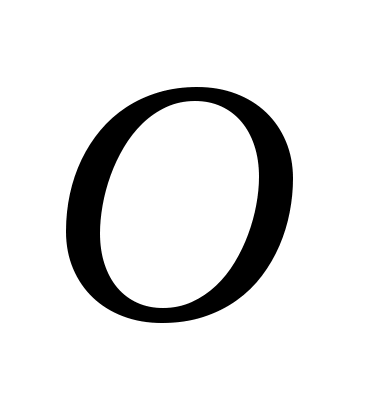 , лежит внутри угла , лежит внутри угла 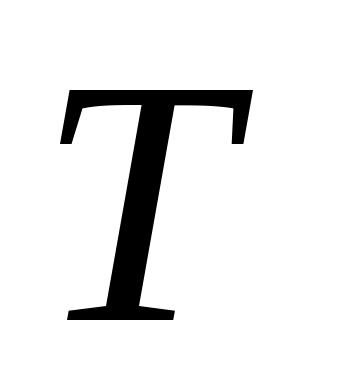 . .
-
№
|
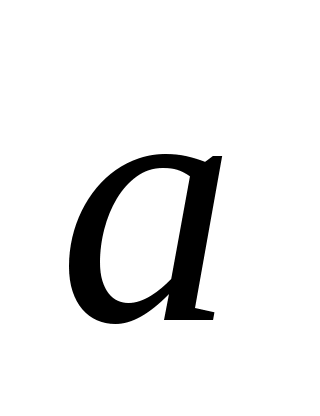
|
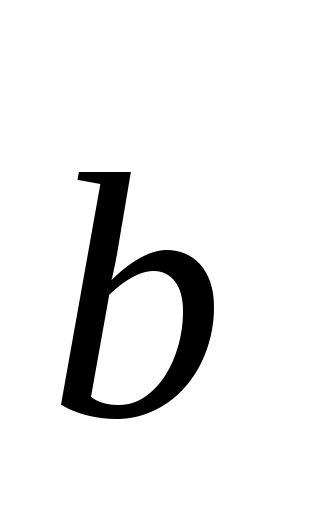
|
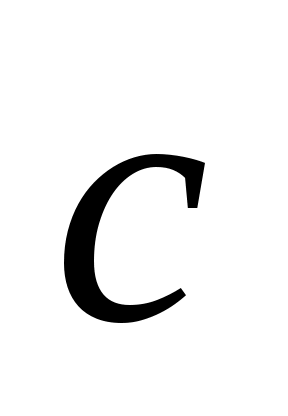
|
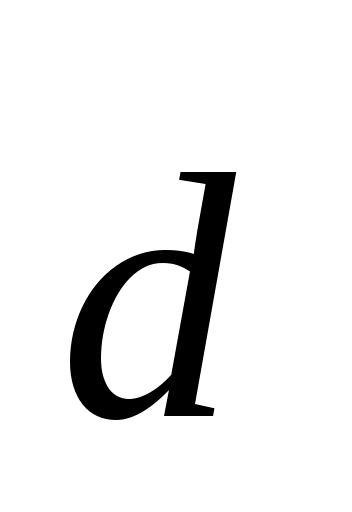
|
1, 19
|
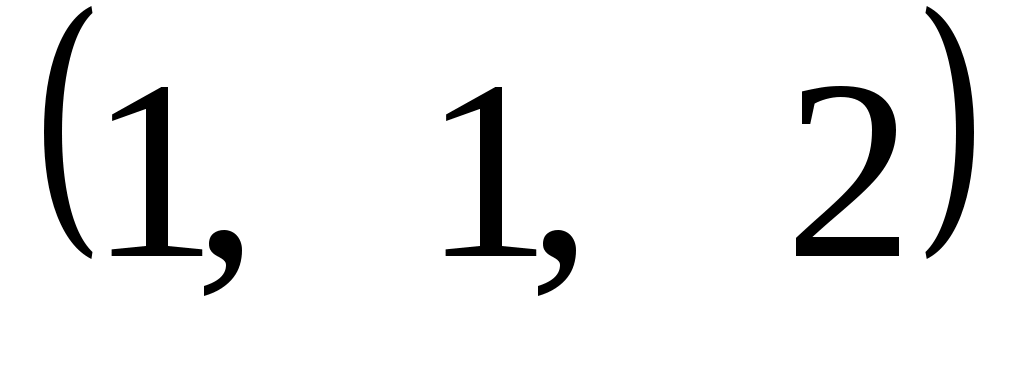
|
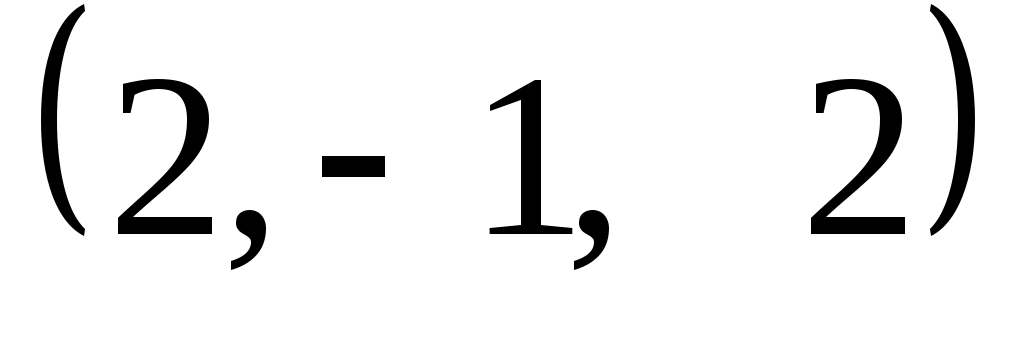
|
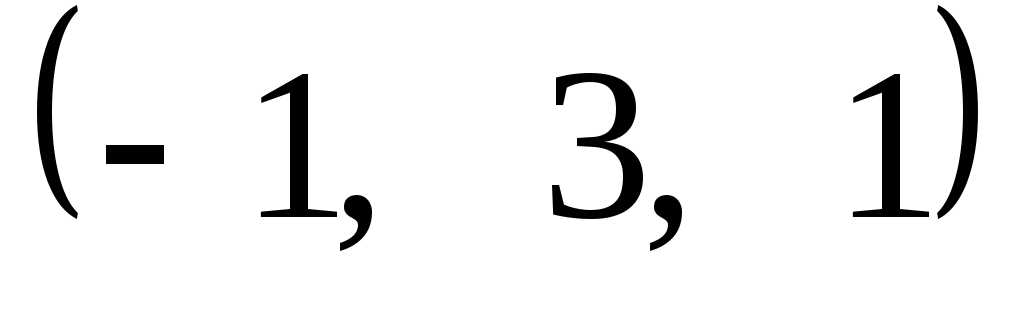
|
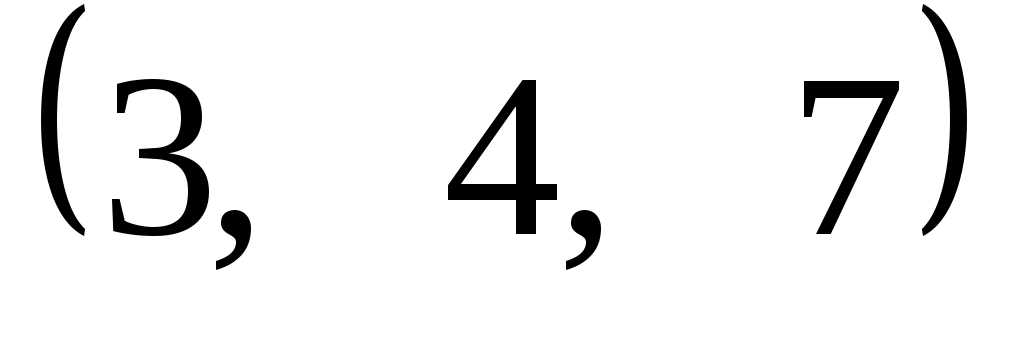
|
2, 20
|
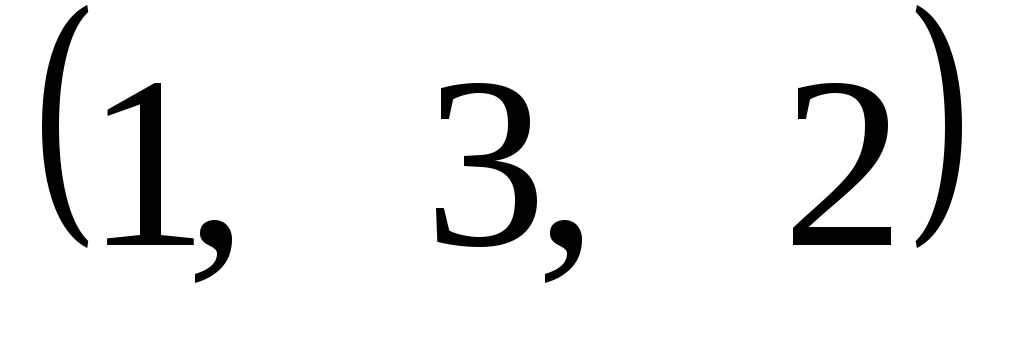
|
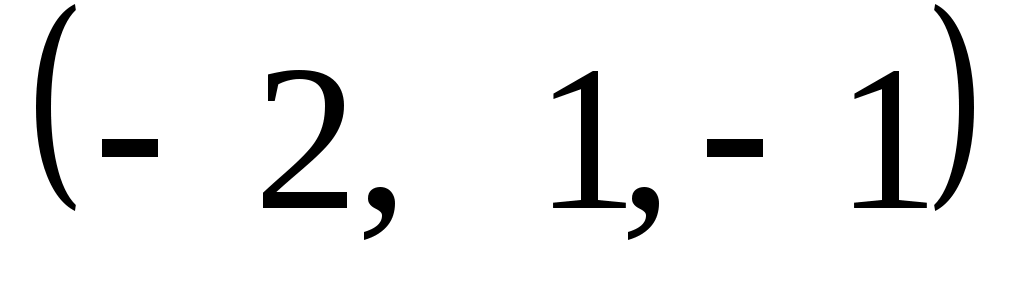
|
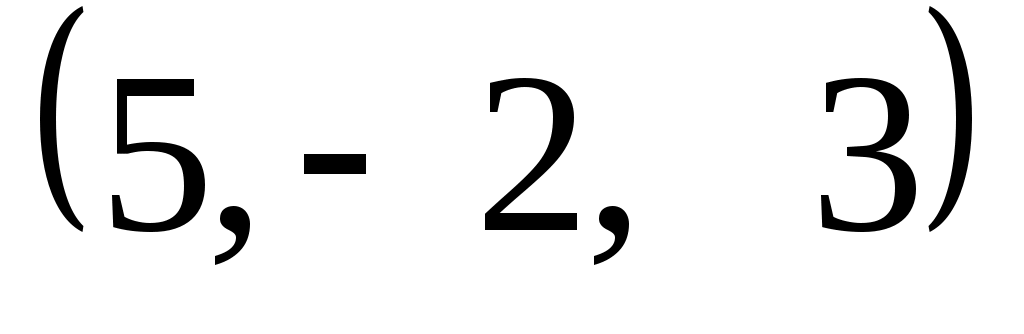
|
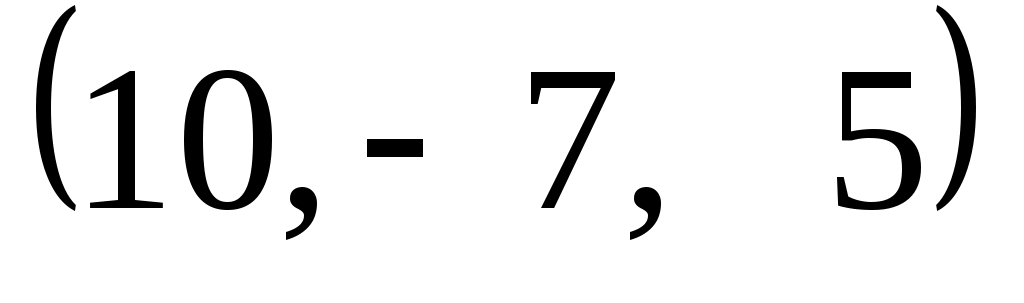
|
3, 21
|
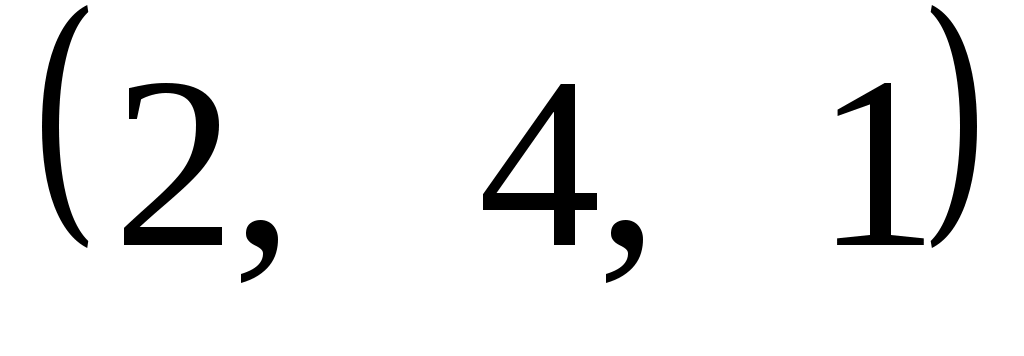
|
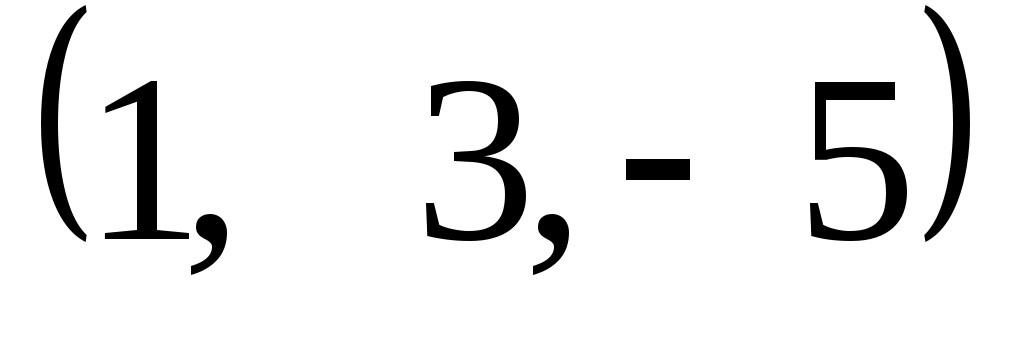
|
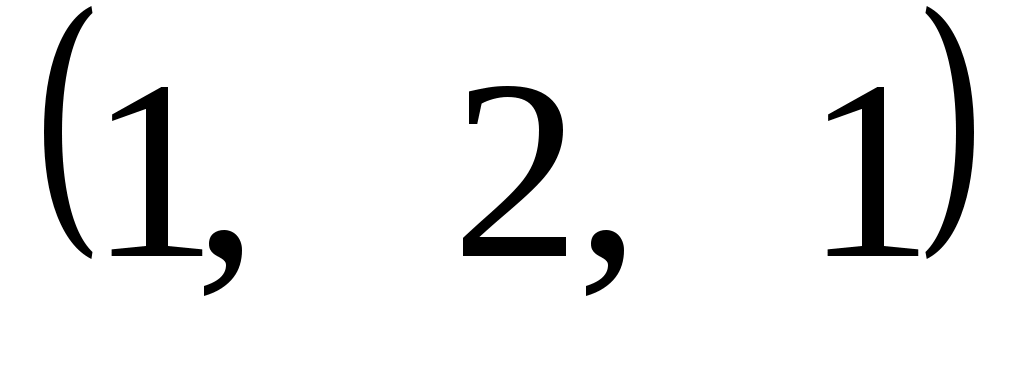
|
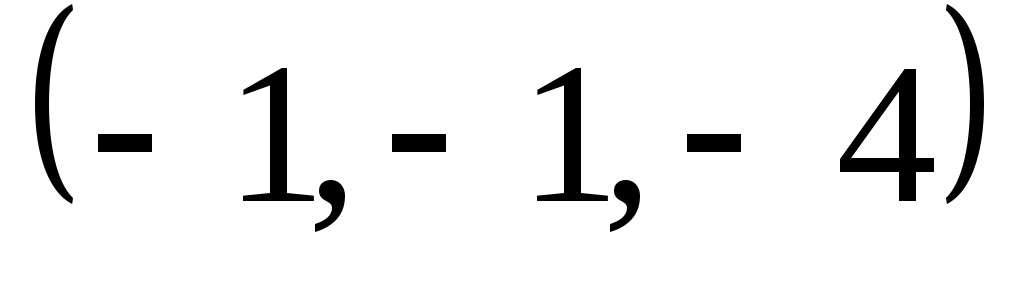
|
4, 22
|
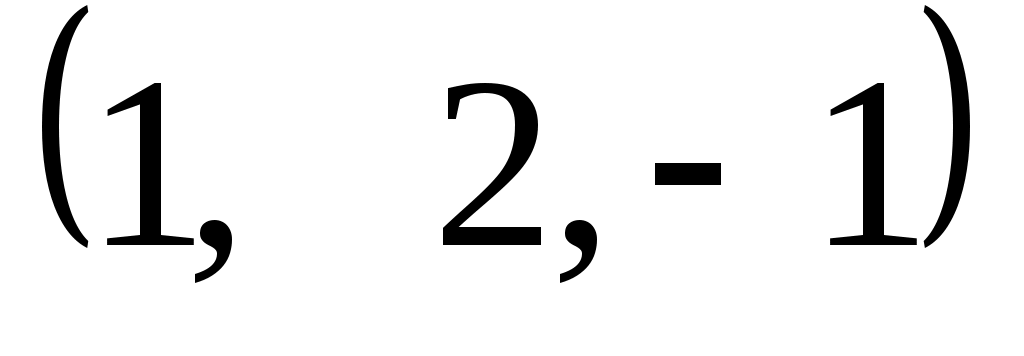
|
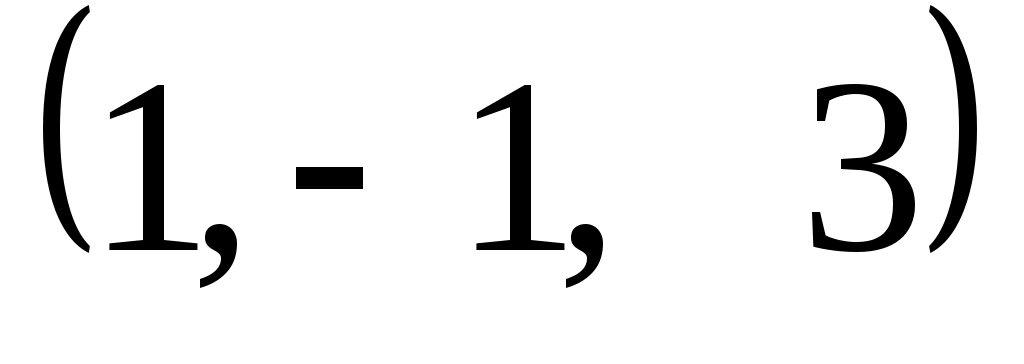
|
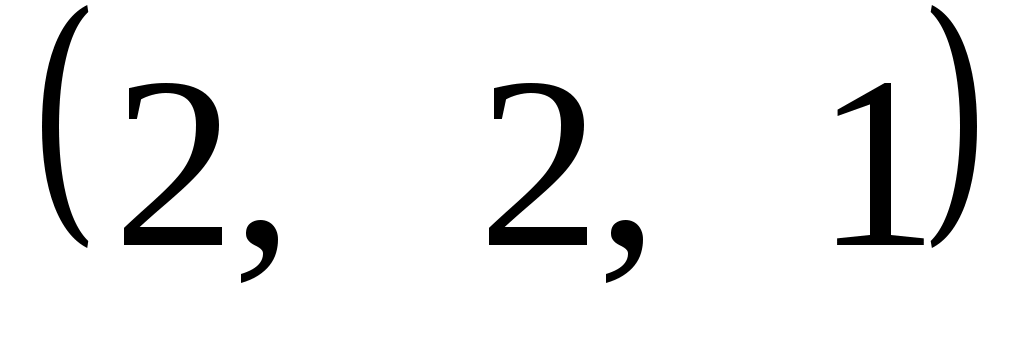
|
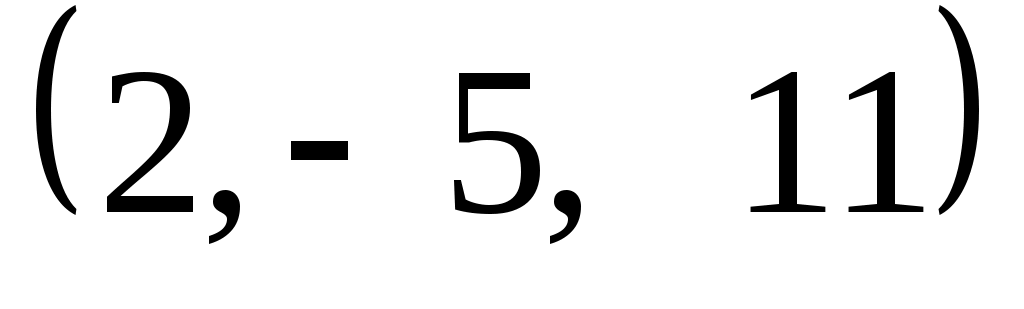
|
5, 23
|
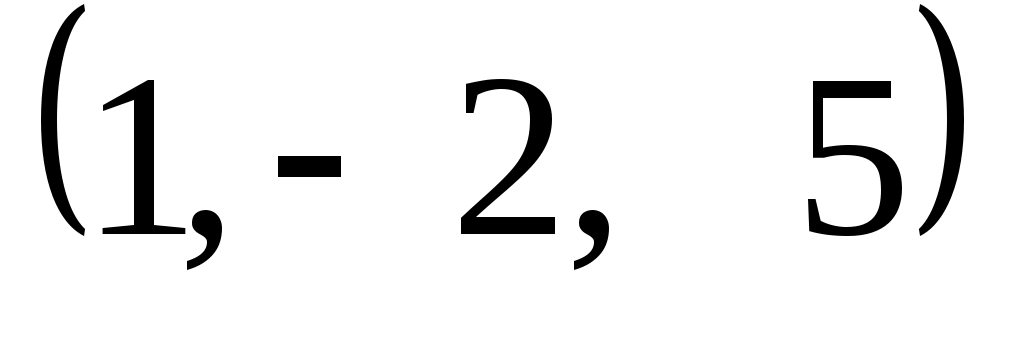
|
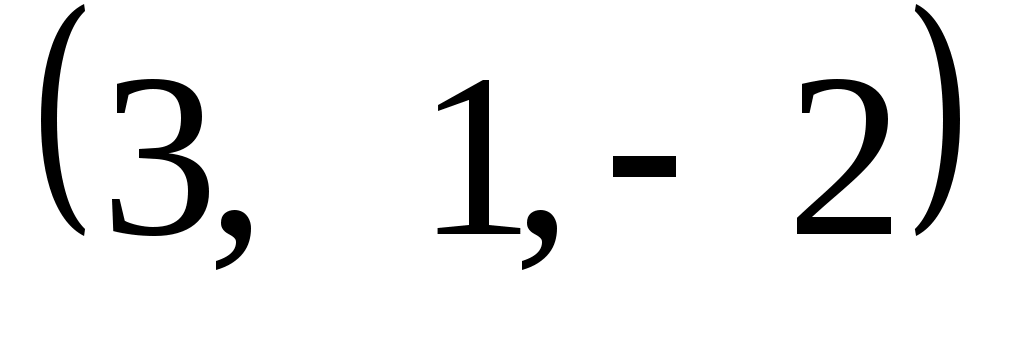
|
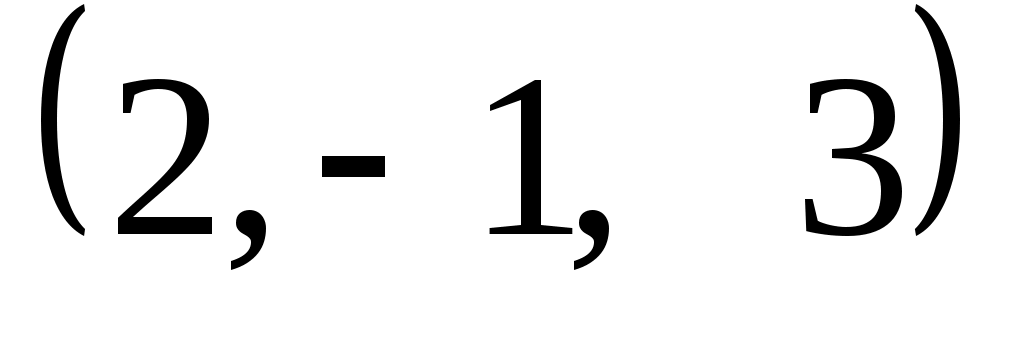
|
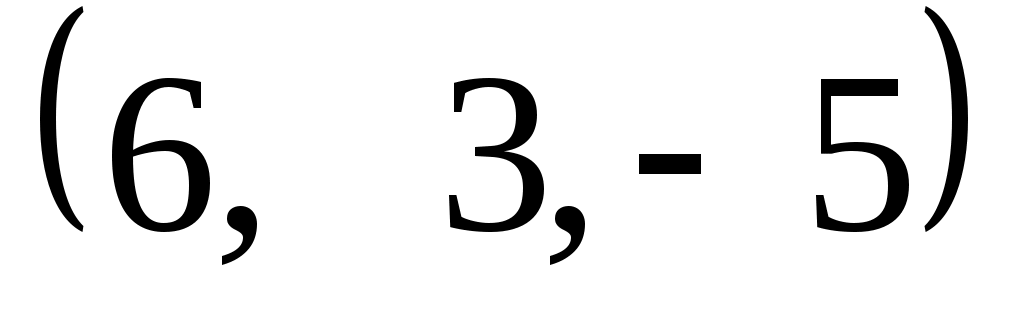
|
6, 24
|
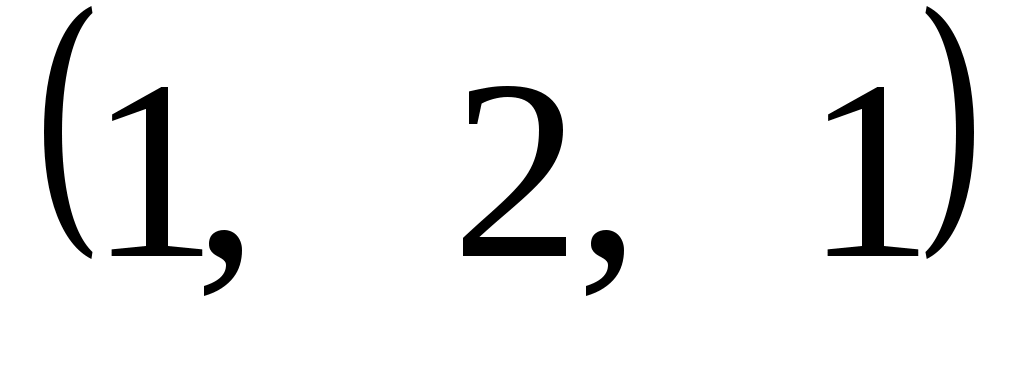
|
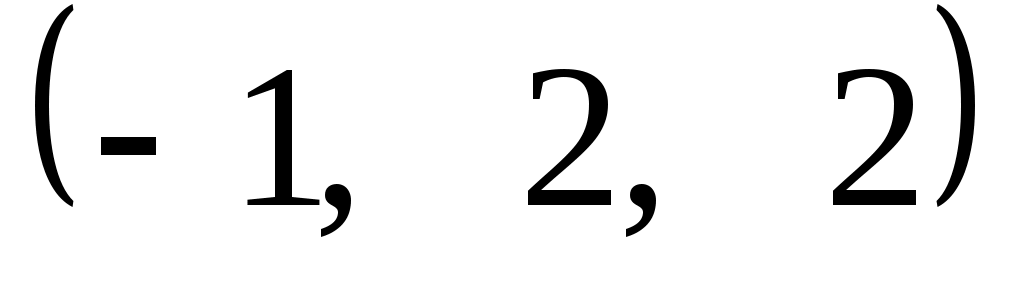
|
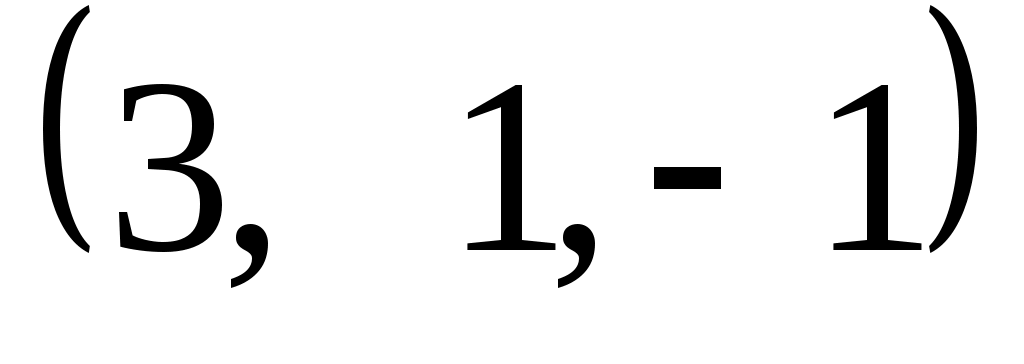
|
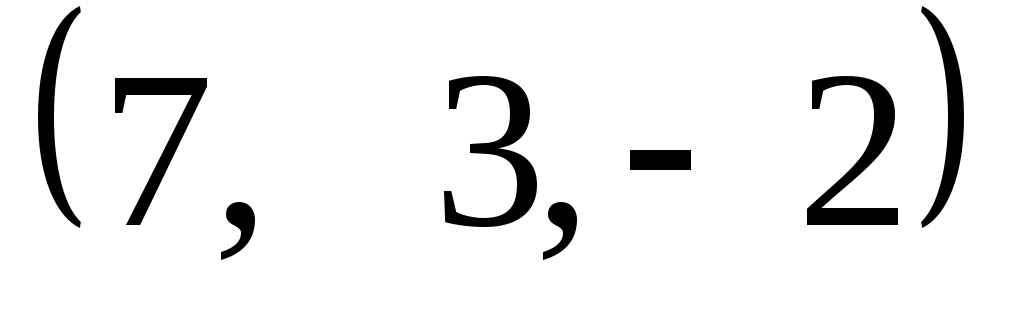
|
7, 25
|
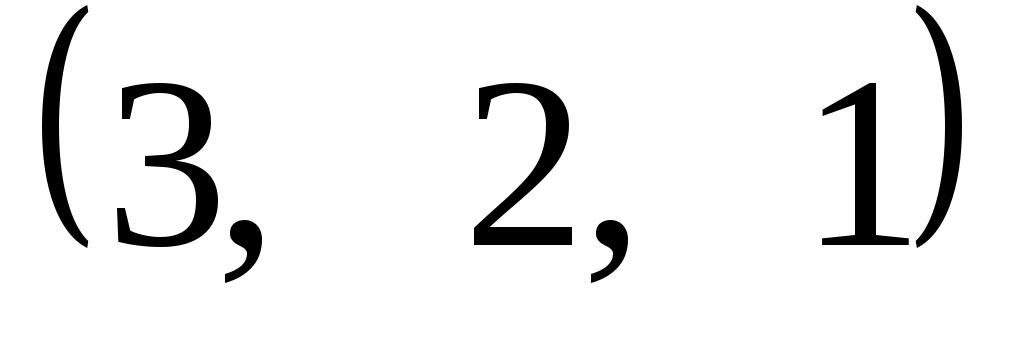
|
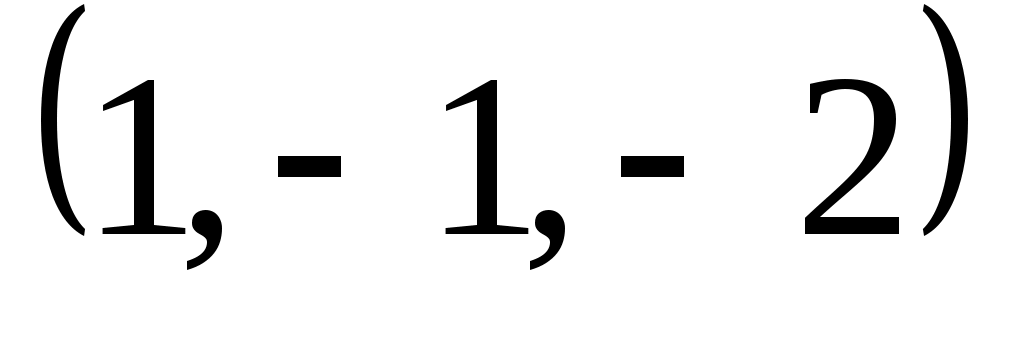
|
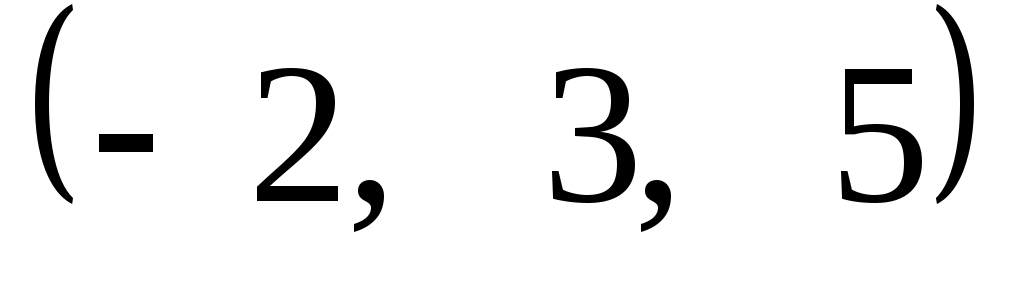
|
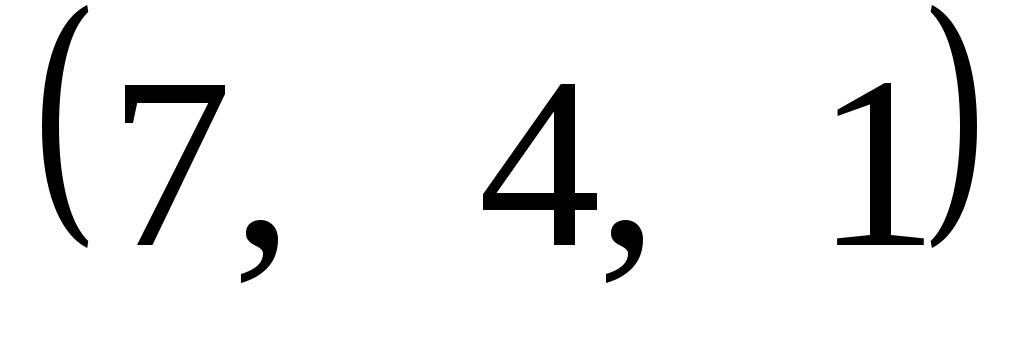
|
8, 26
|
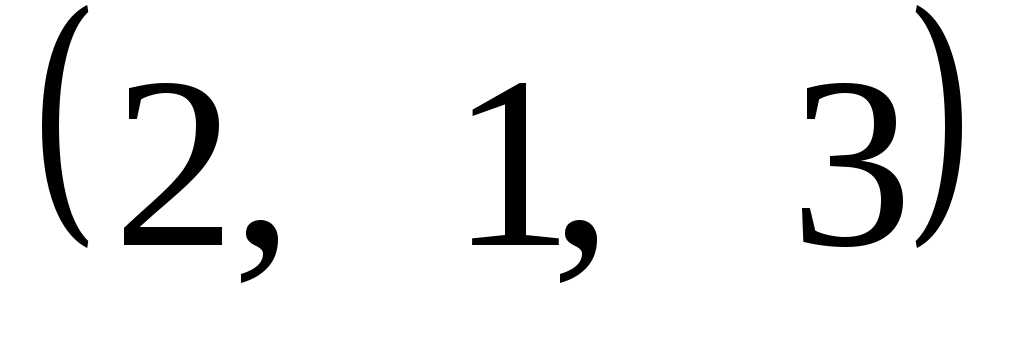
|
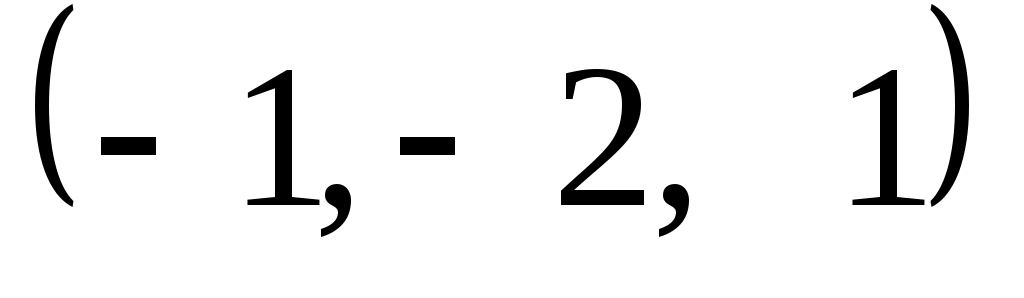
|
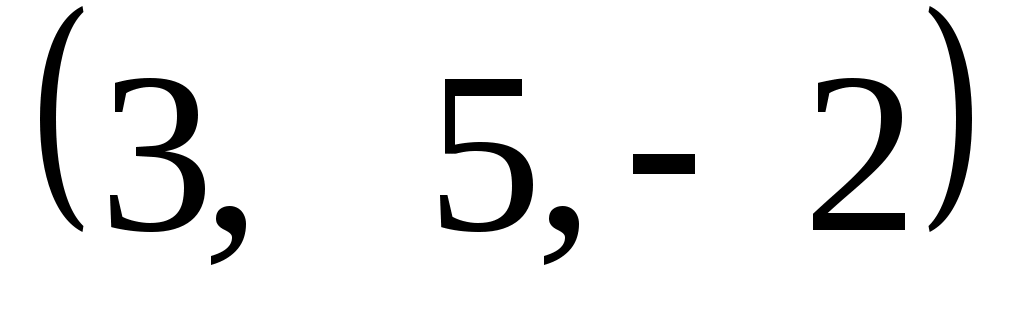
|
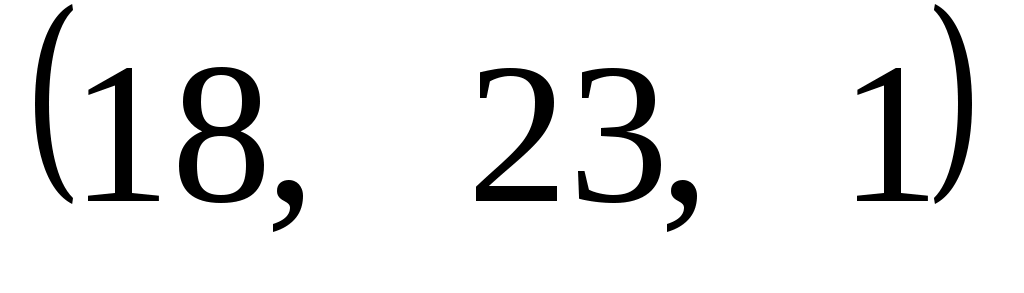
|
9, 27
|
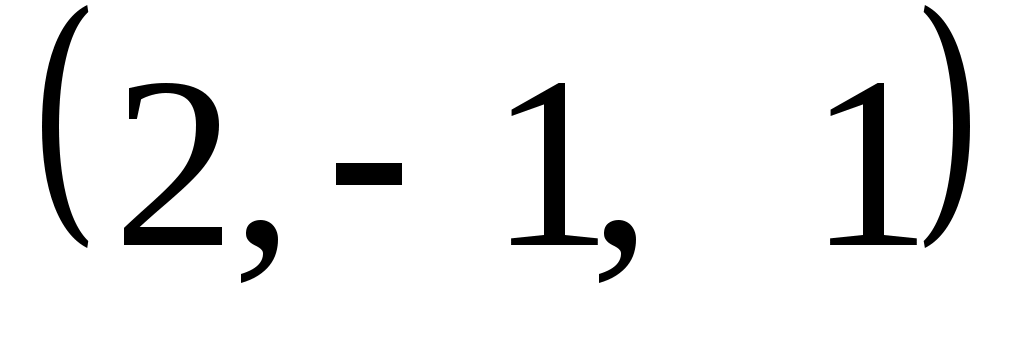
|
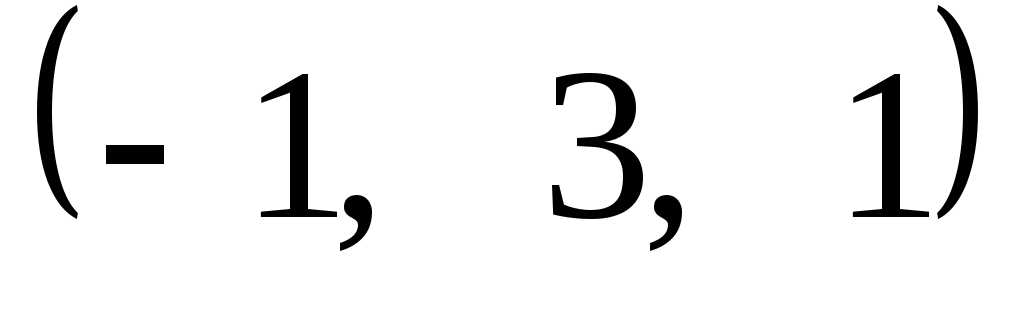
|
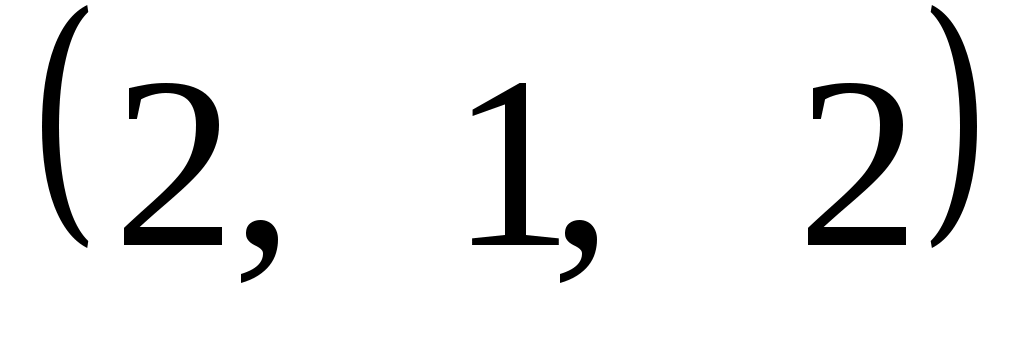
|
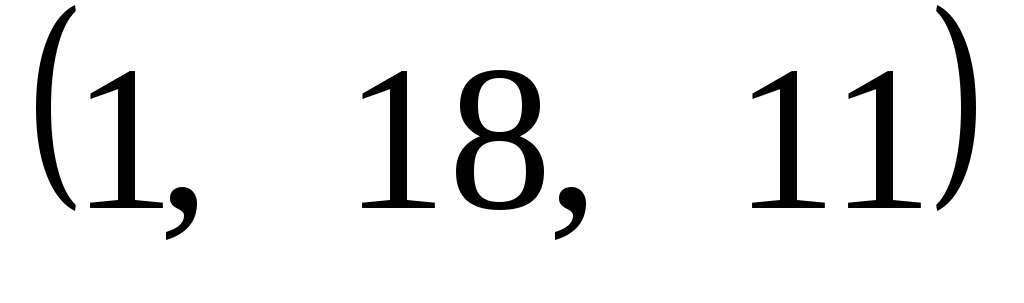
|
10, 28
|
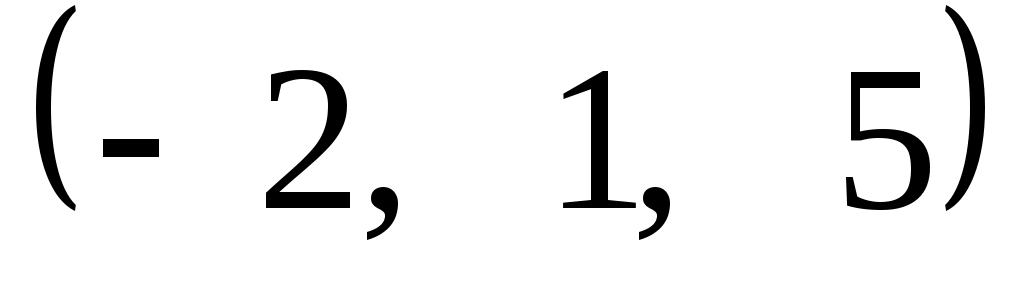
|
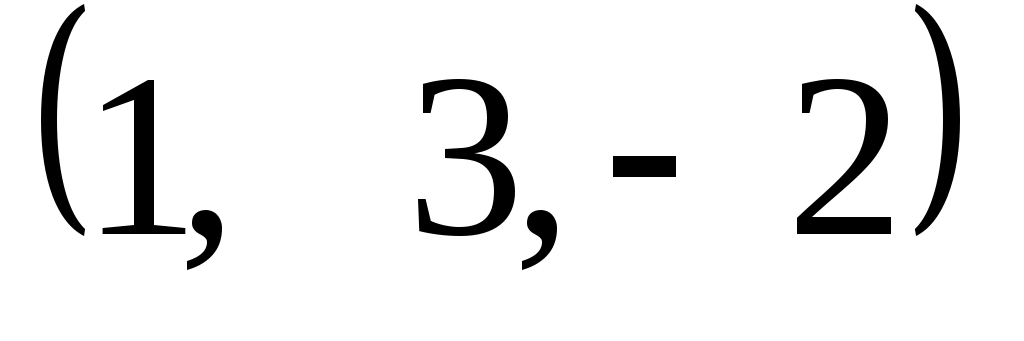
|
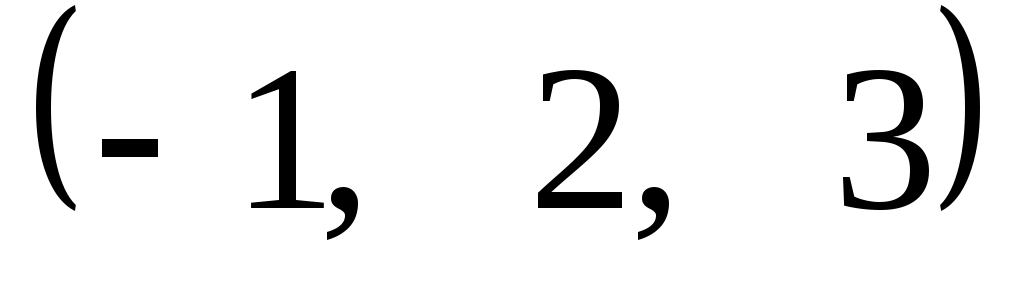
|
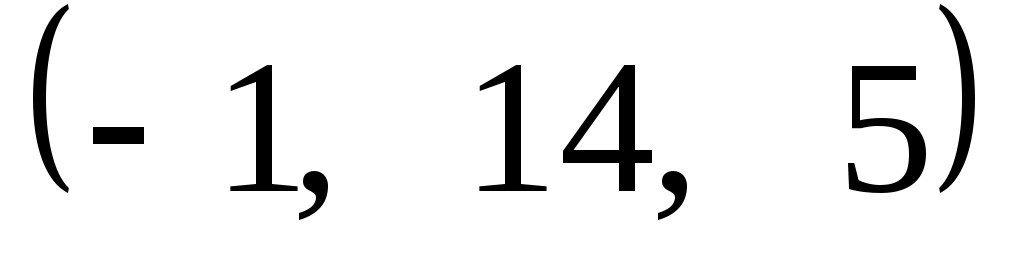
|
11, 29
|
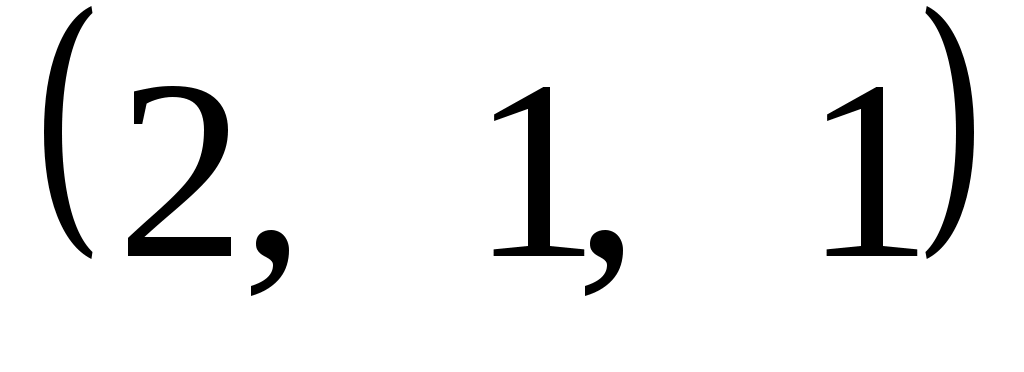
|
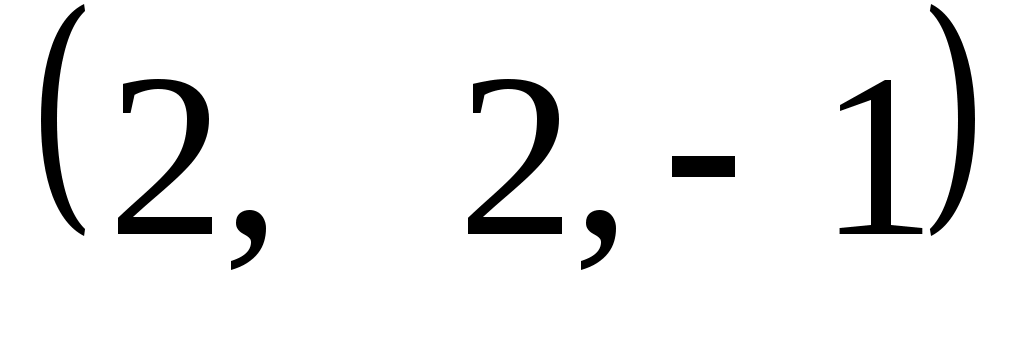
|
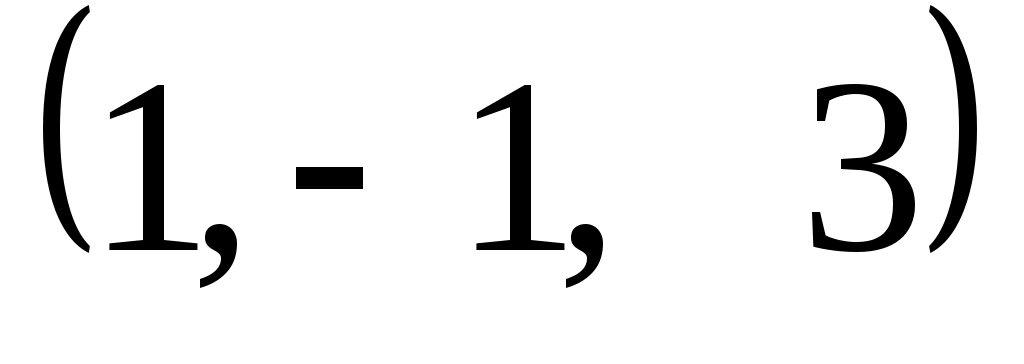
|
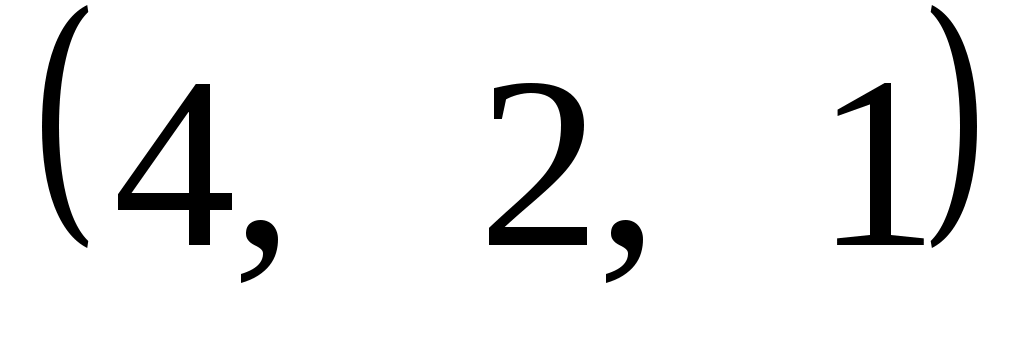
|
12, 30
|
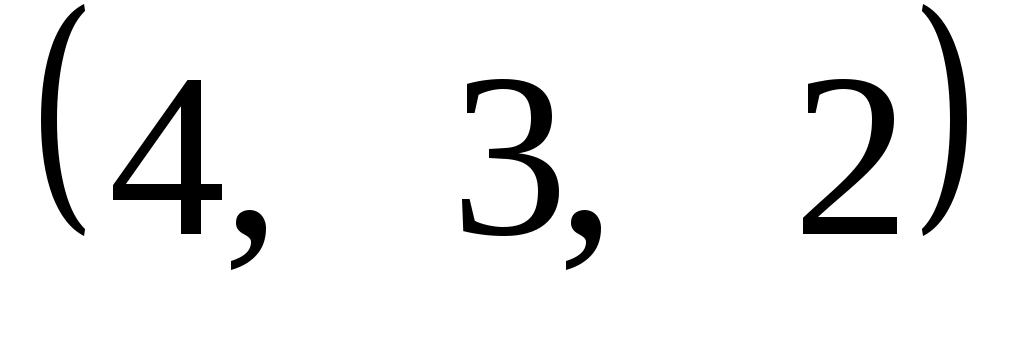
|
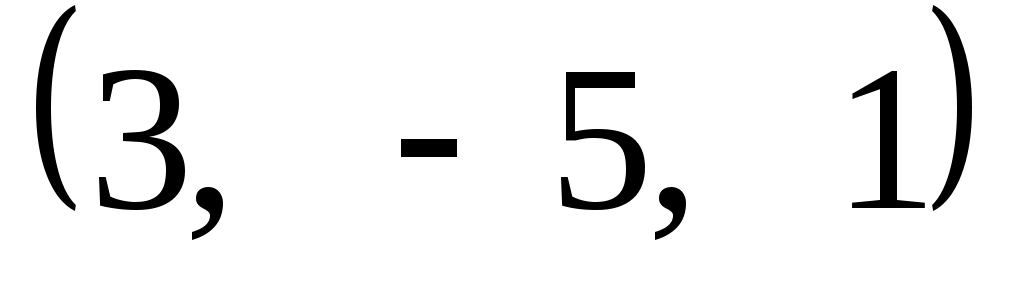
|
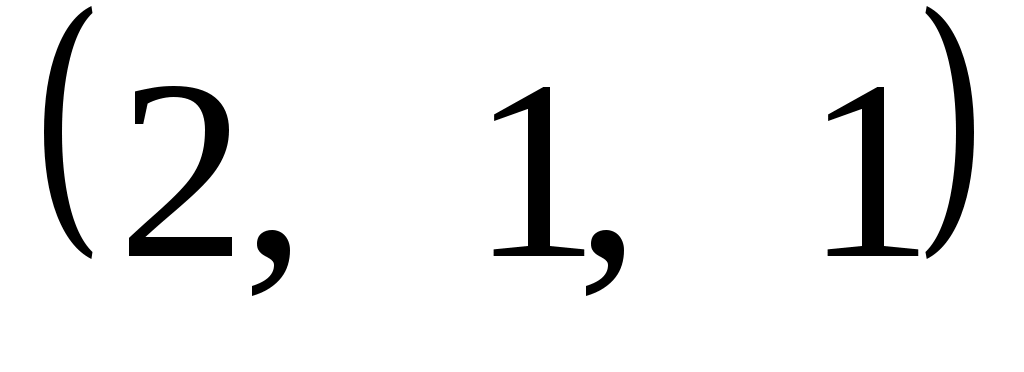
|
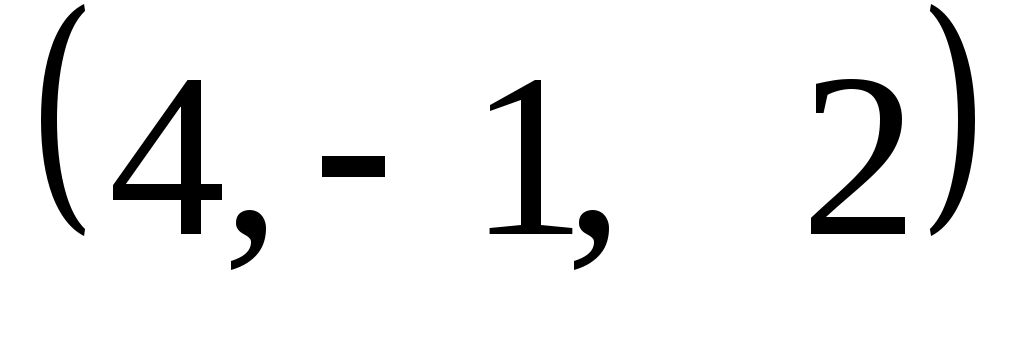
|
13, 16
|
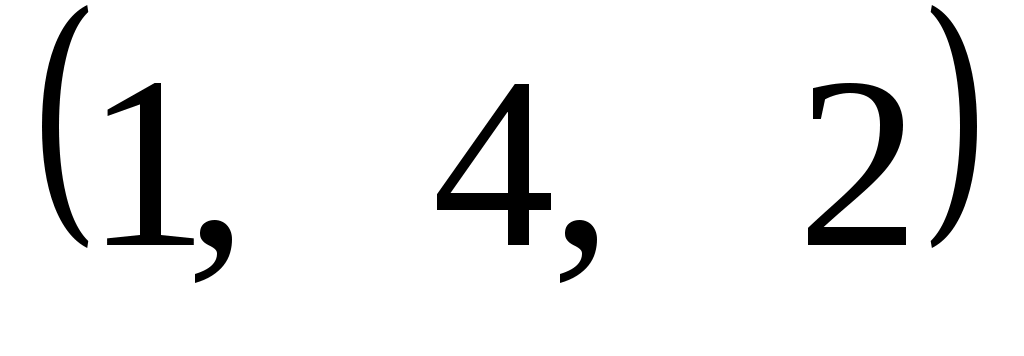
|
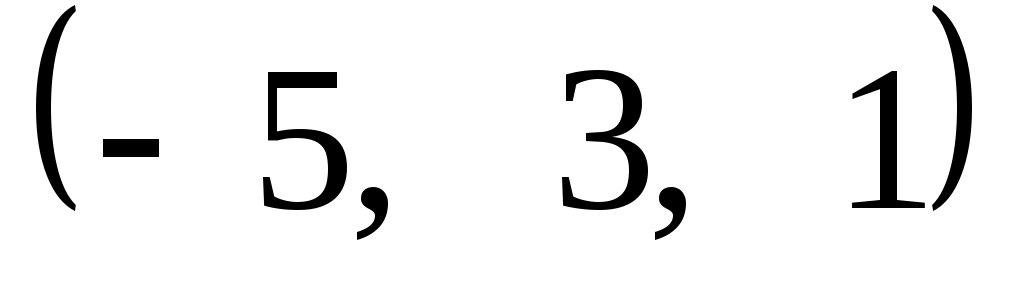
|
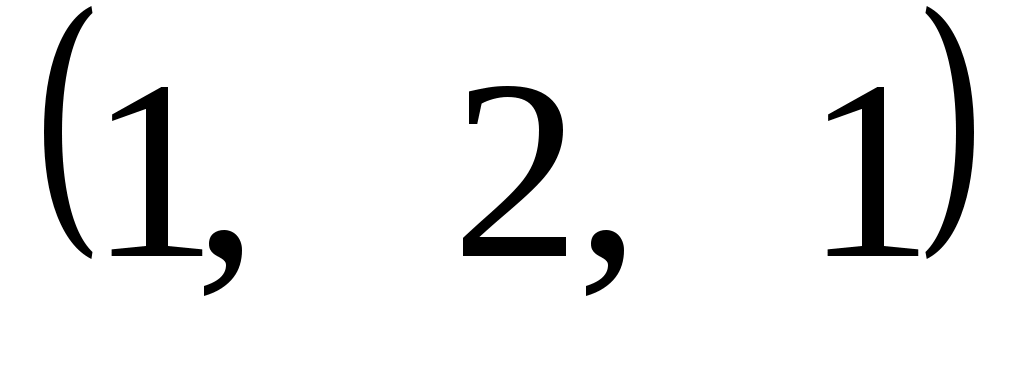
|
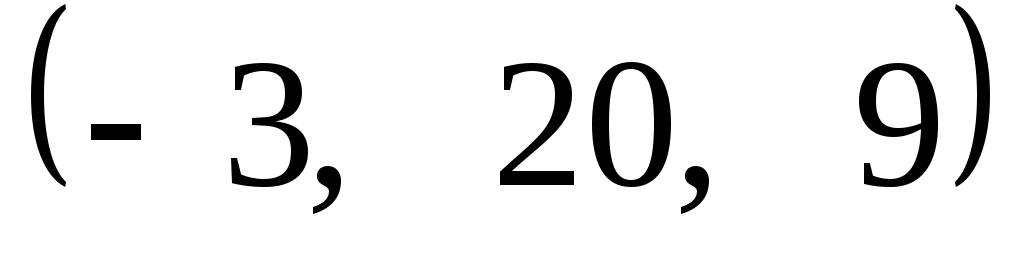
|
14, 17
|
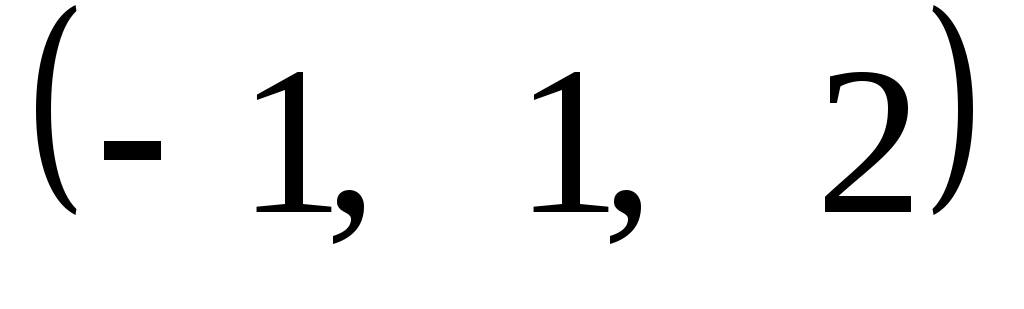
|
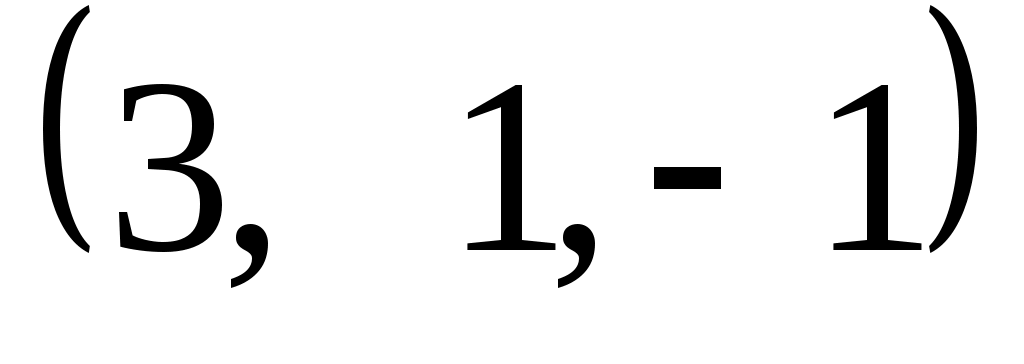
|
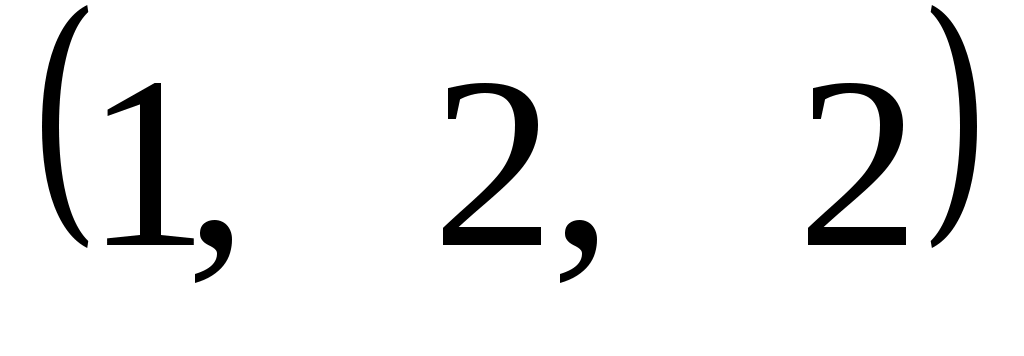
|
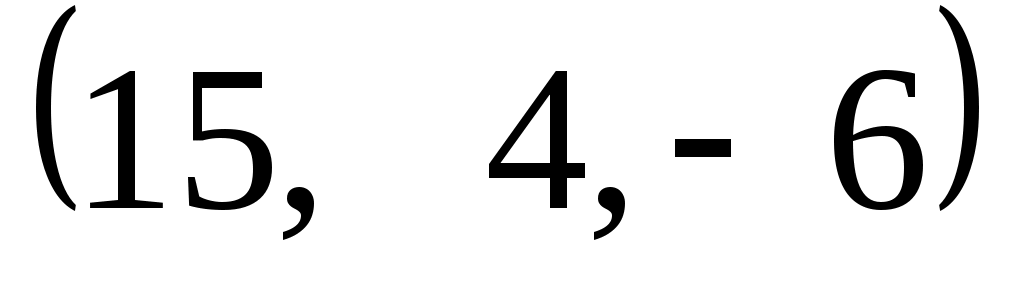
|
15, 18
|
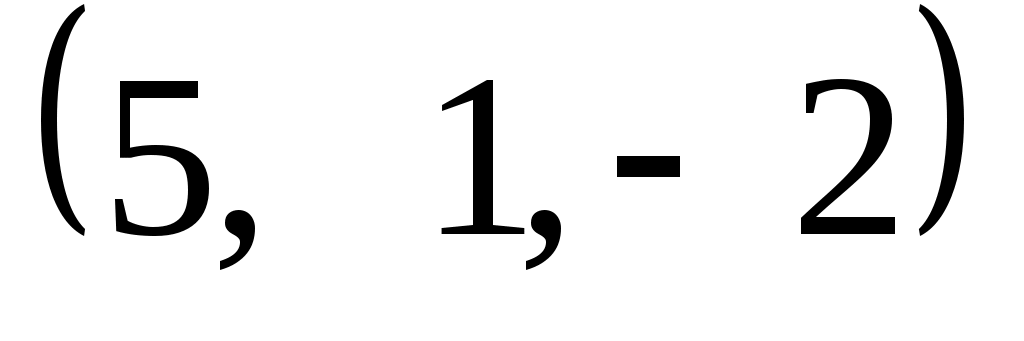
|
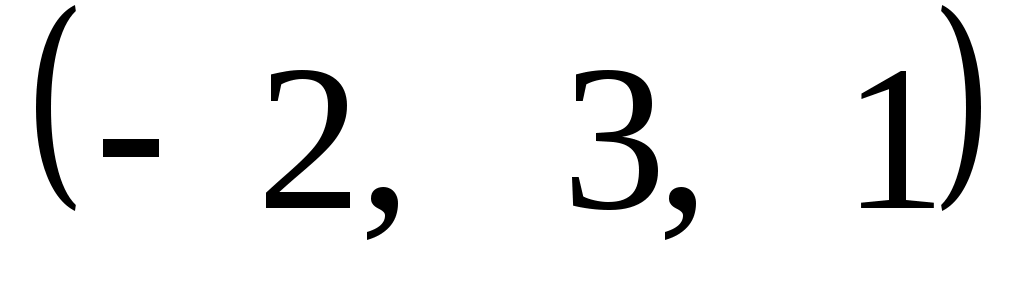
|
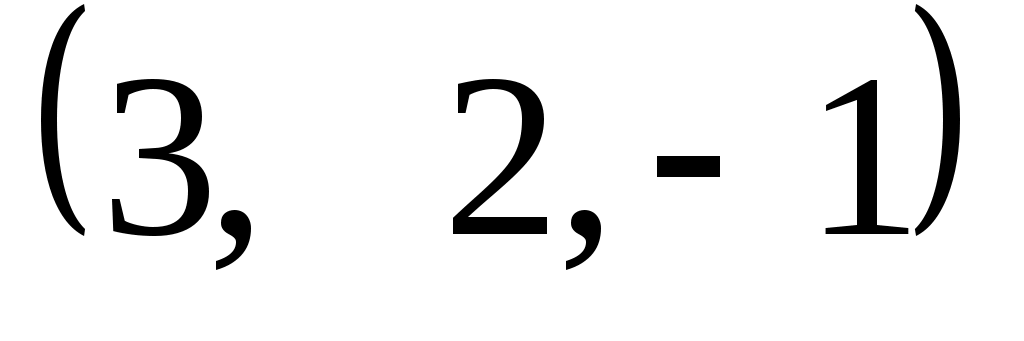
|
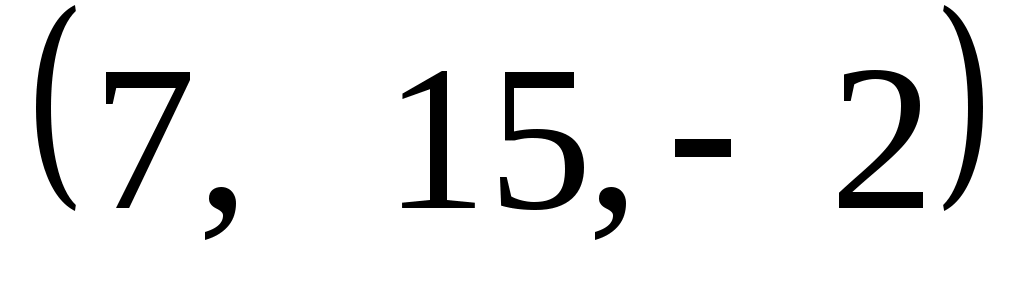
|
Задание 10.
Доказать, что заданное множество 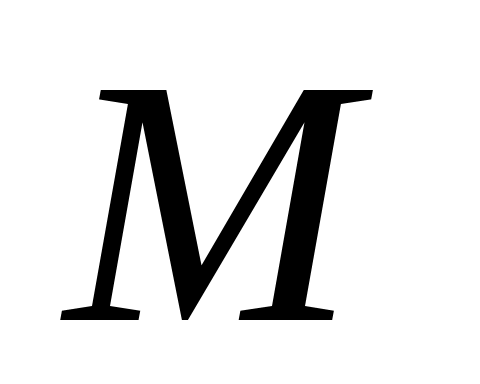 многочленов с указанными условиями является линейным подпространством в пространстве многочленов с указанными условиями является линейным подпространством в пространстве 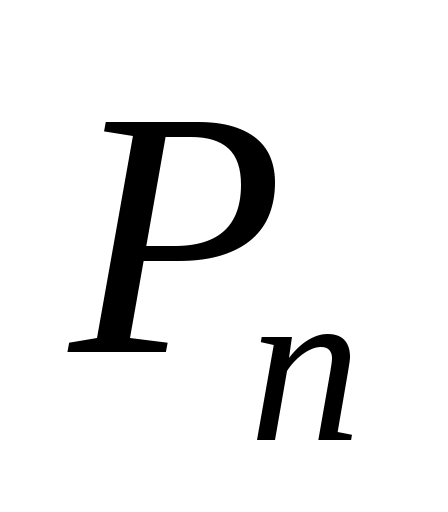 многочленов степени не выше многочленов степени не выше 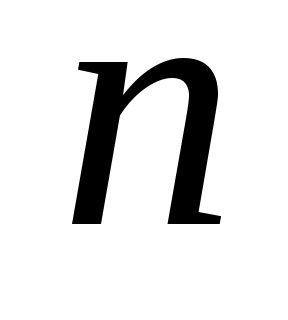 c действительными коэффициентами. Запись c действительными коэффициентами. Запись 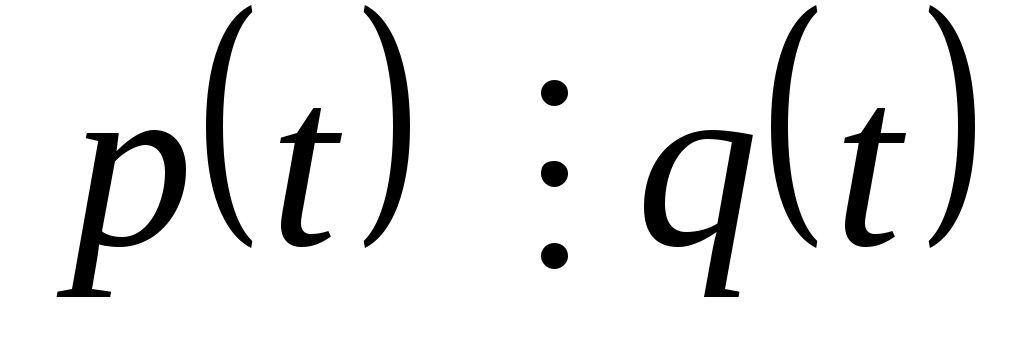 означает, что многочлен означает, что многочлен 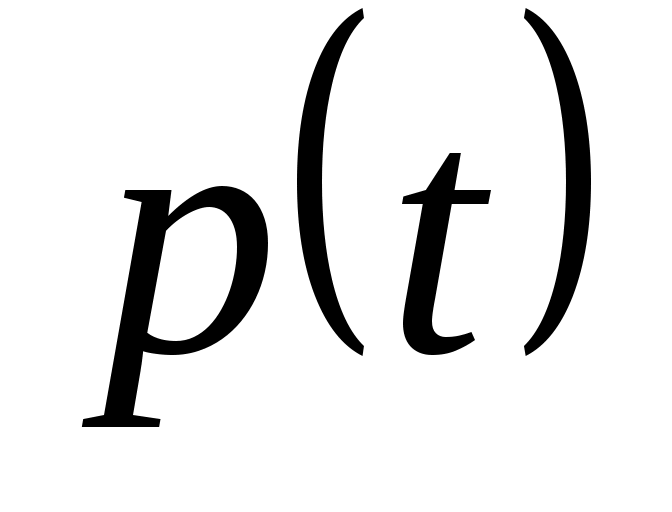 делится на многочлен делится на многочлен 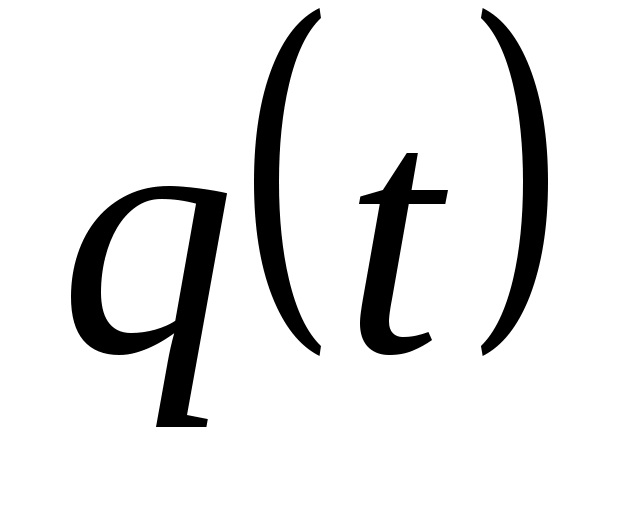 без остатка. без остатка.
Найти базис и размерность М.
Дополнить базис М до базиса Pn.
-
№
|
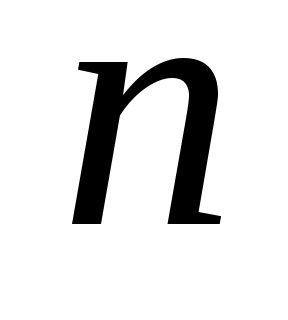
|
Условия на 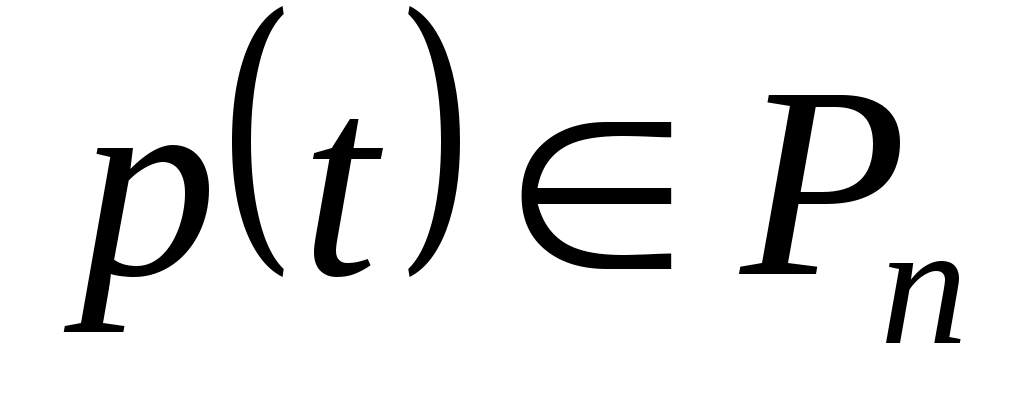
|
1
|
3
|
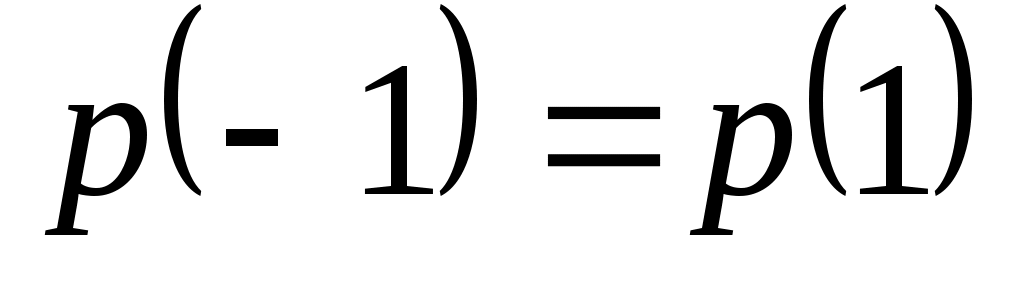
|
2
|
3
|
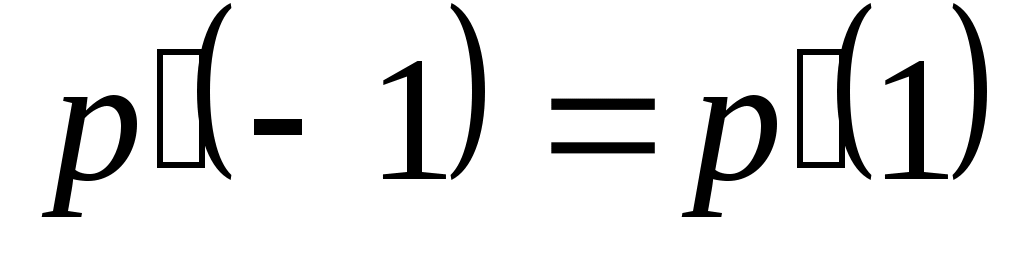
|
3
|
3
|
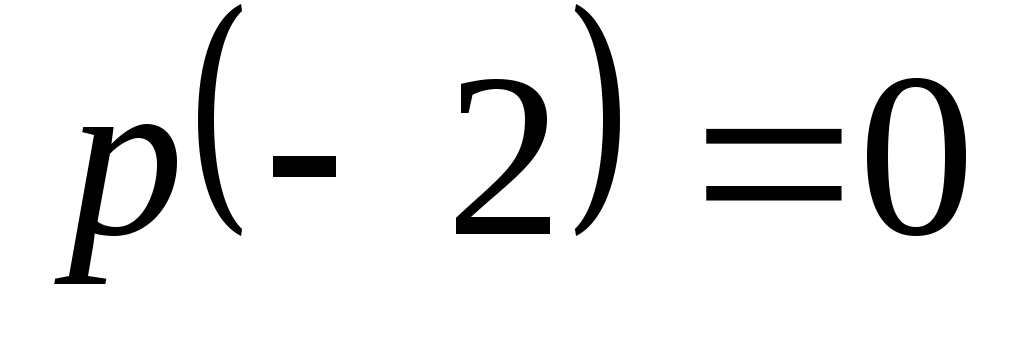
|
4
|
4
|
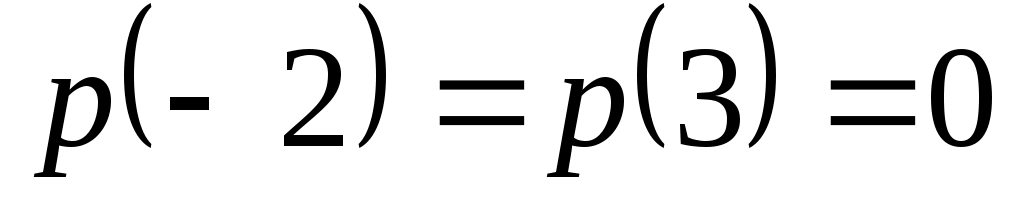
|
5
|
4
|
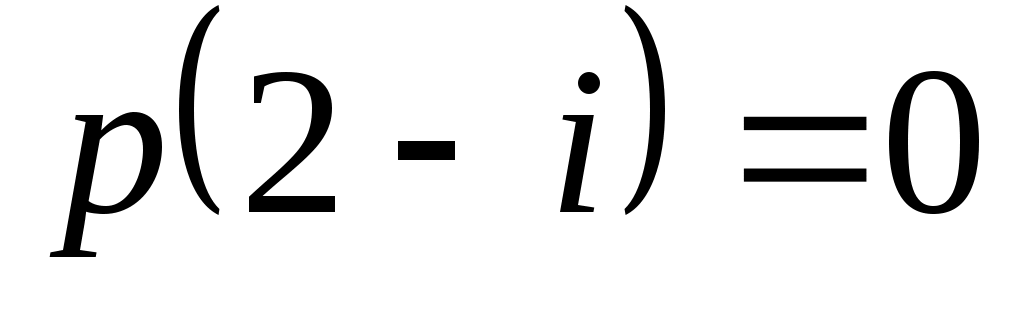
|
6
|
3
|
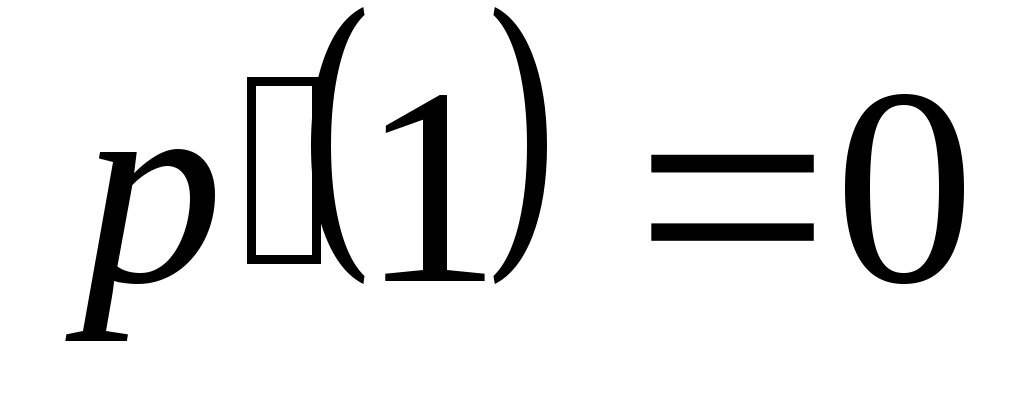
|
7
|
3
|
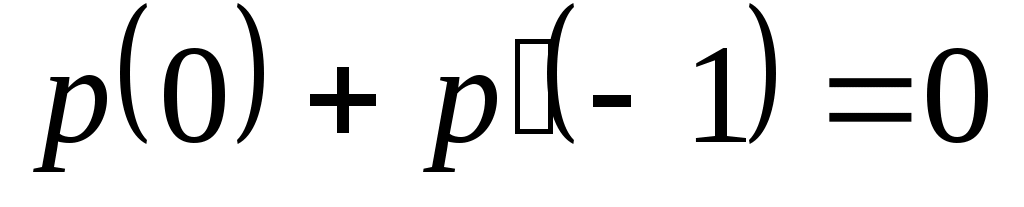
|
8
|
4
|
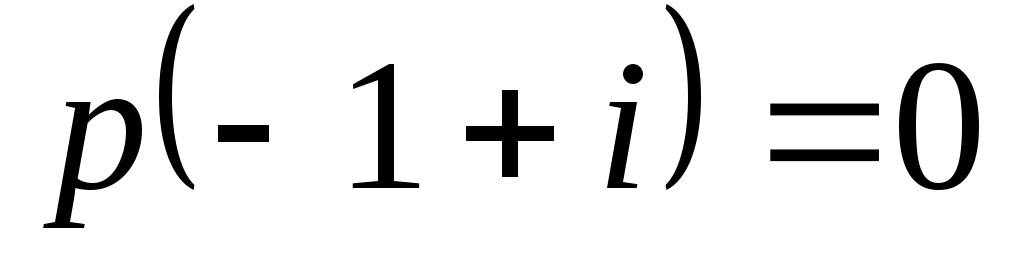
|
9
|
4
|
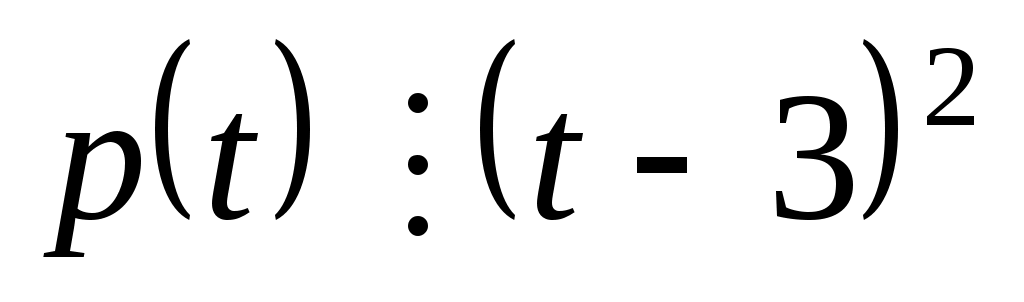
|
10
|
3
|
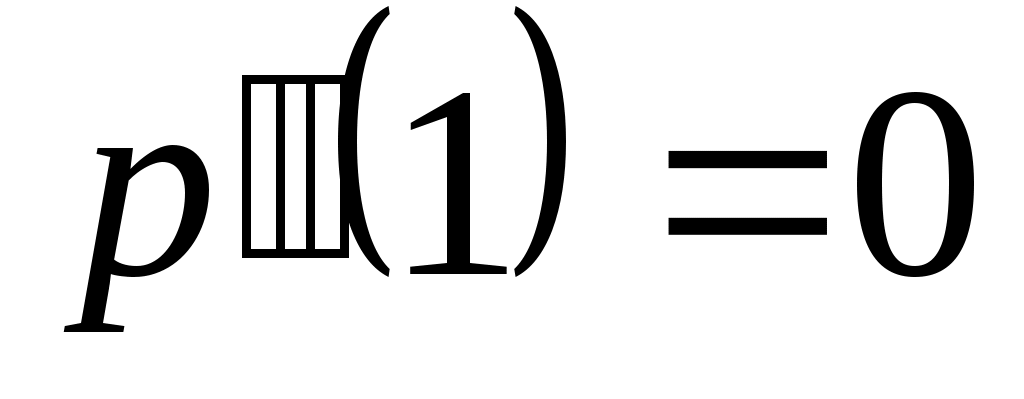
|
11
|
4
|
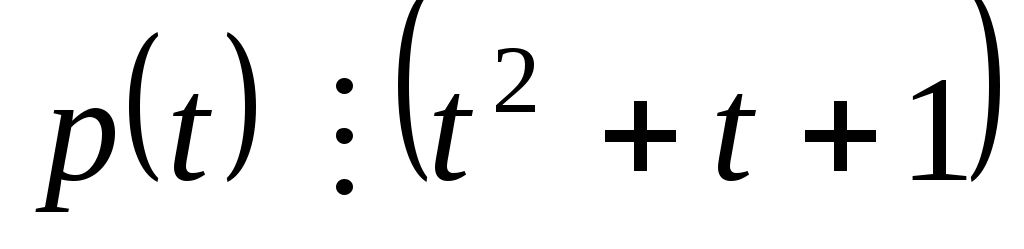
|
12
|
3
|
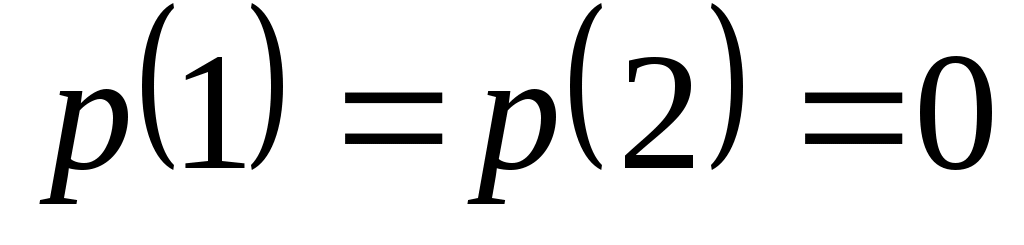
|
13
|
3
|
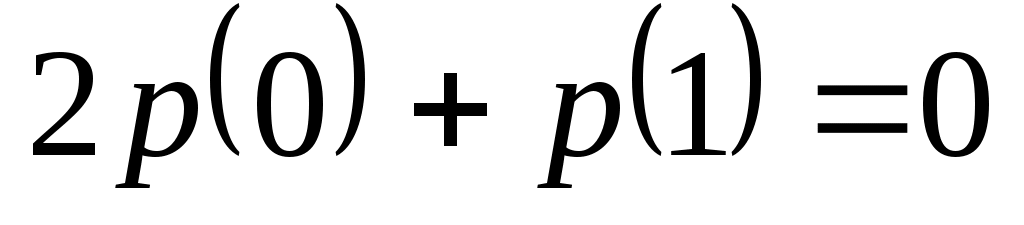
|
14
|
3
|
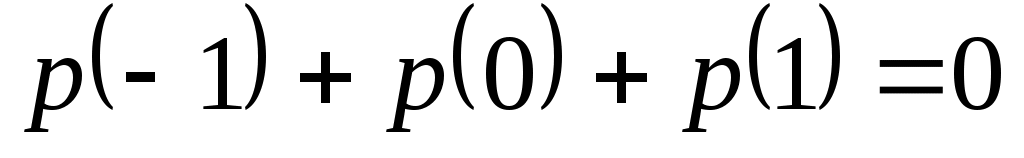
|
15
|
3
|
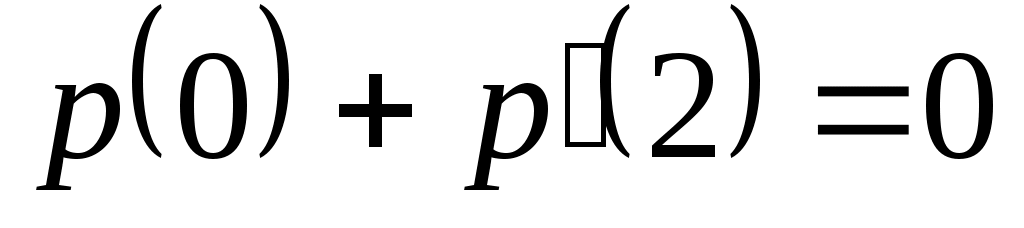
|
16
|
3
|
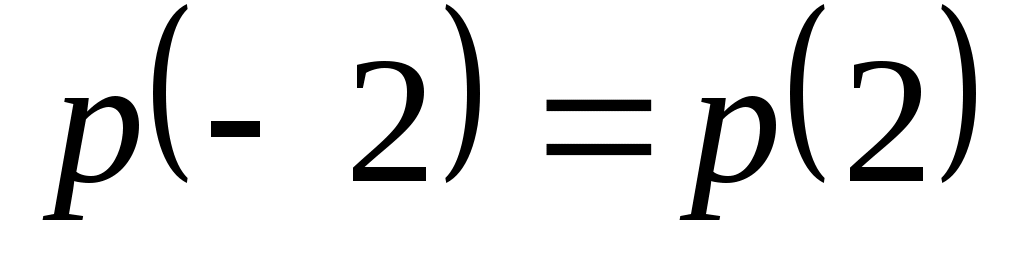
|
17
|
4
|
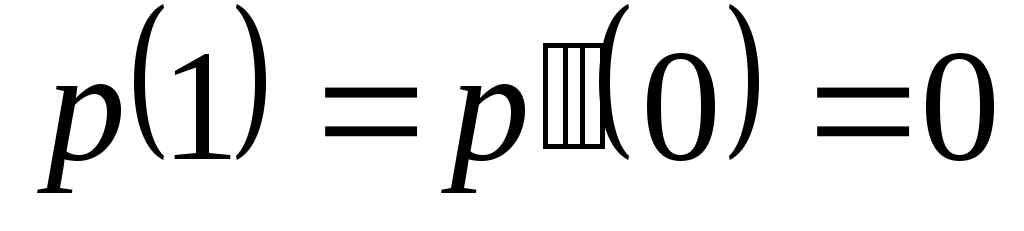
|
18
|
3
|
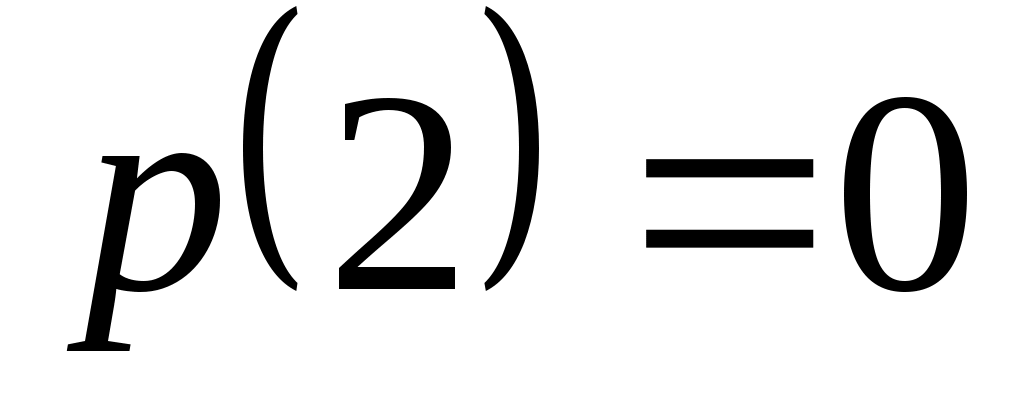
|
19
|
4
|
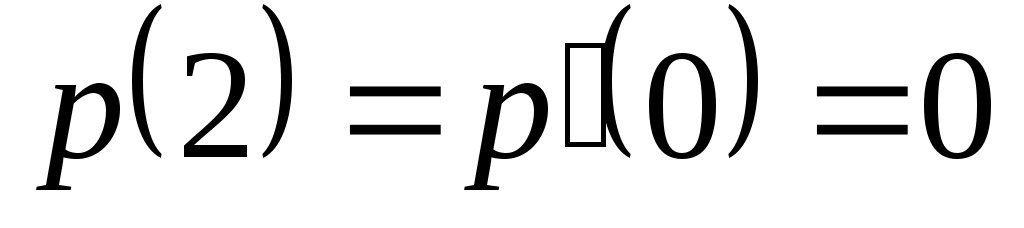
|
20
|
4
|
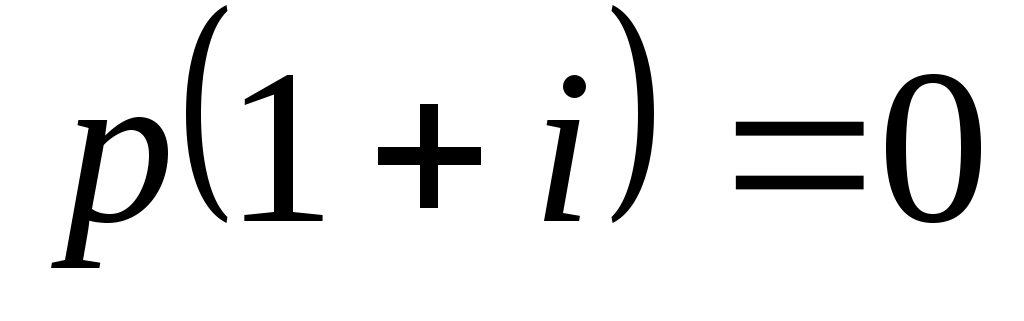
|
21
|
3
|
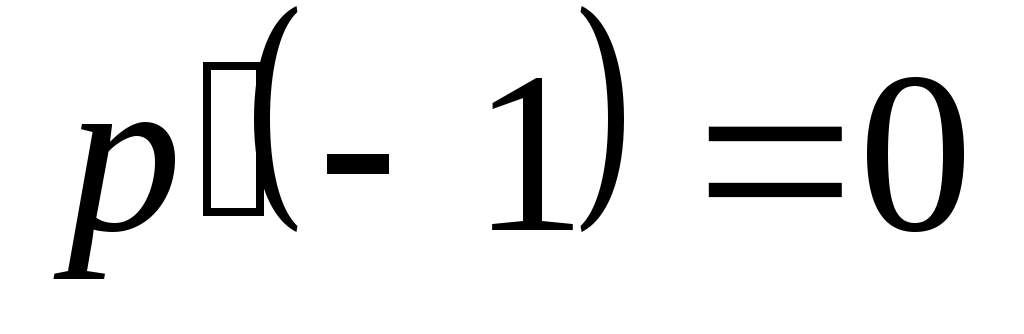
|
22
|
3
|
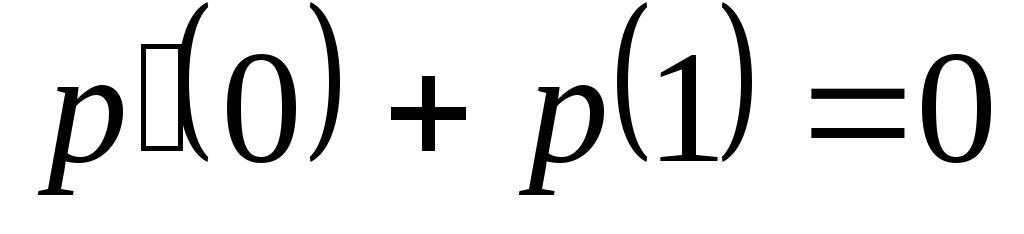
|
23
|
4
|
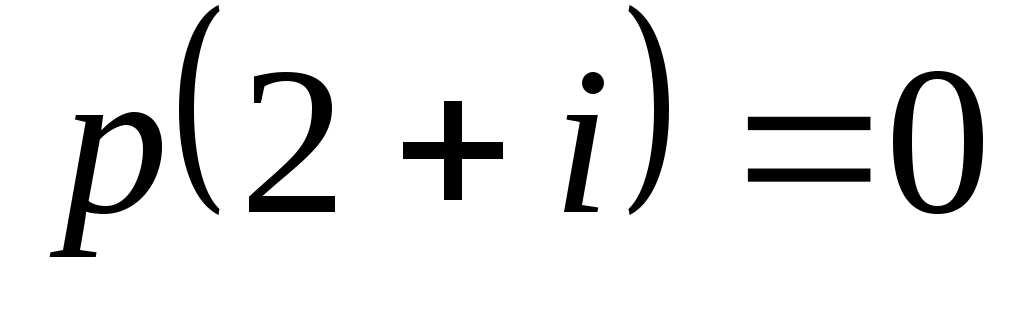
|
24
|
4
|
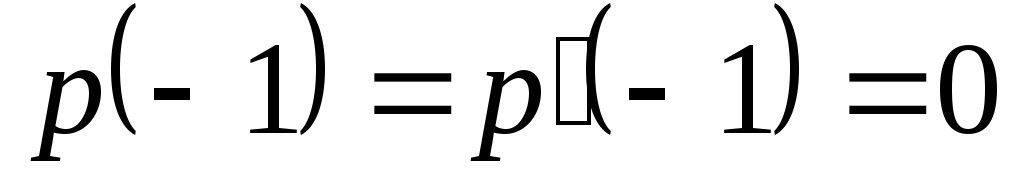
|
25
|
3
|
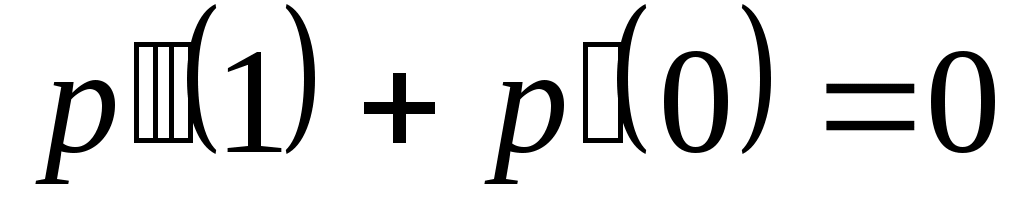
|
26
|
4
|
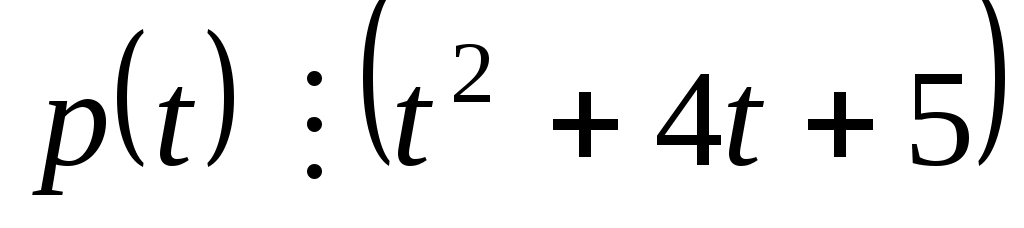
|
27
|
3
|
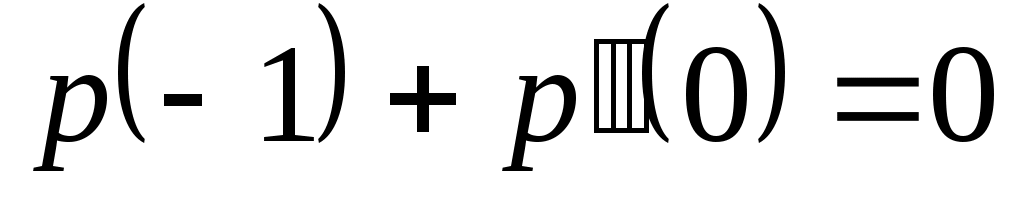
|
28
|
3
|
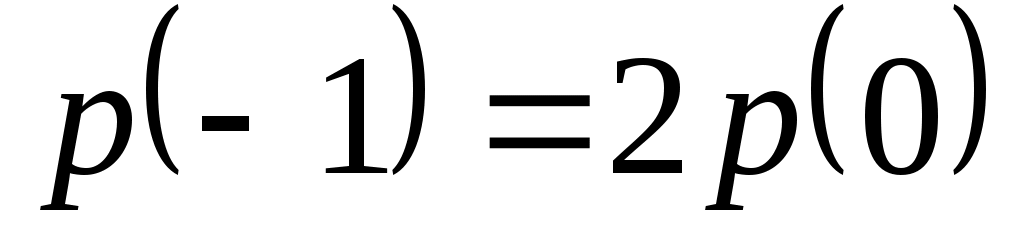
|
29
|
3
|
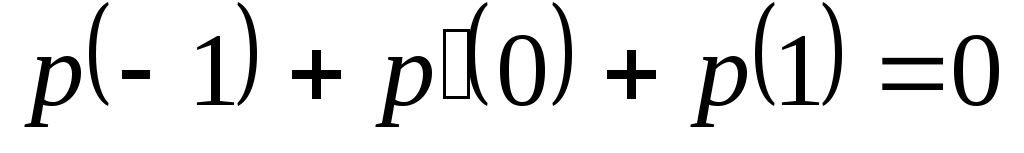
|
30
|
4
|
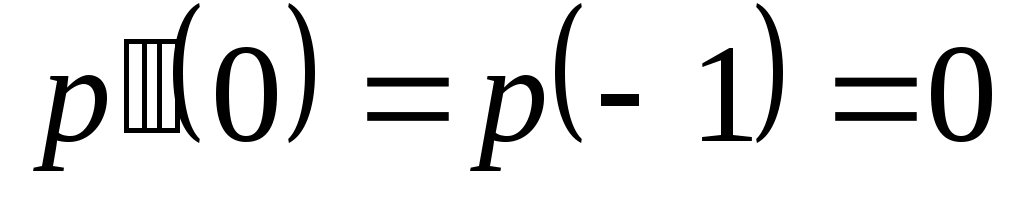
| |
 Скачать 1.22 Mb.
Скачать 1.22 Mb.