№
|
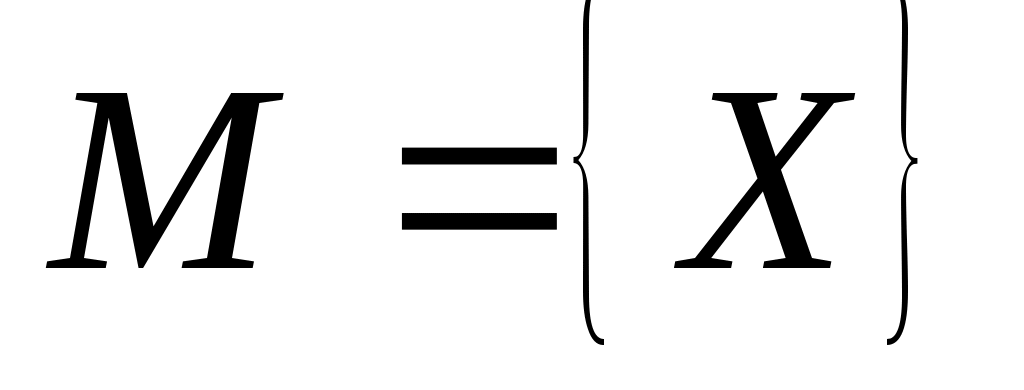
| В |
1
|
 - решения матричного уравнения - решения матричного уравнения 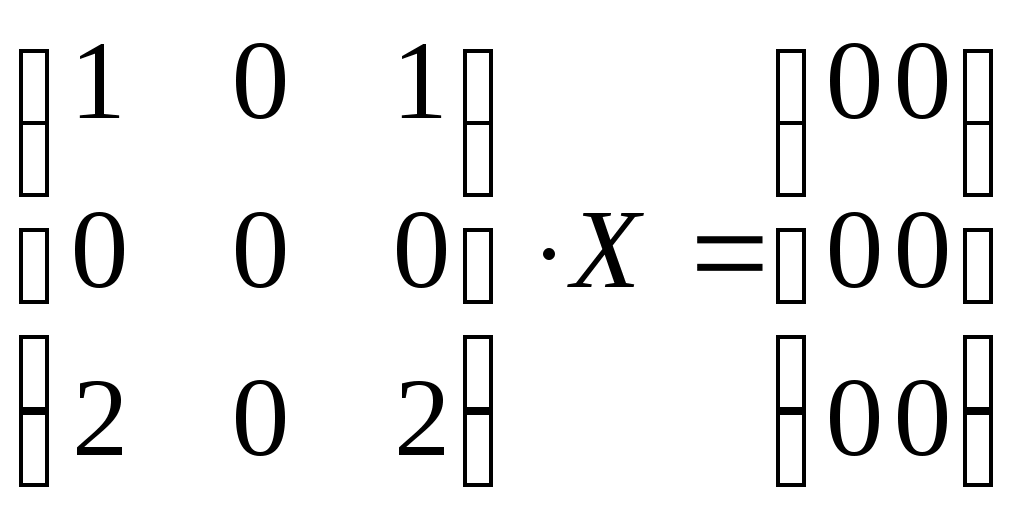
|

|
2
|
 - решения матричного уравнения - решения матричного уравнения 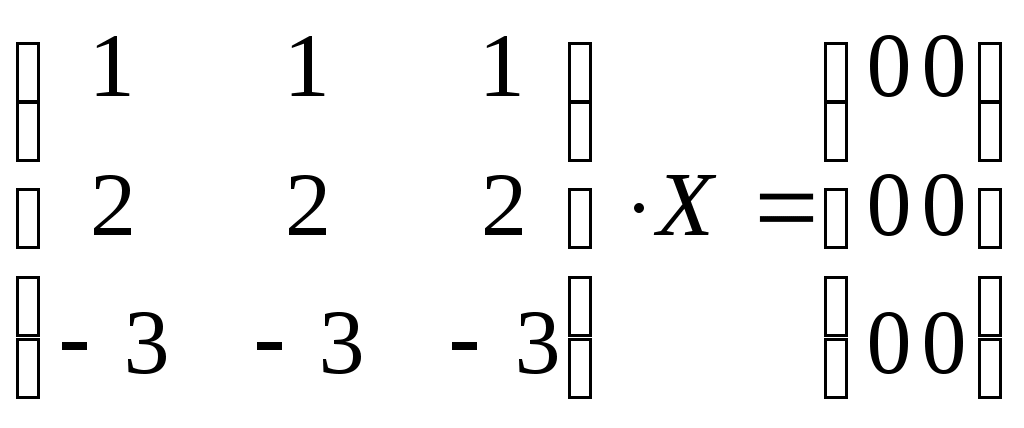
|
|
3
|
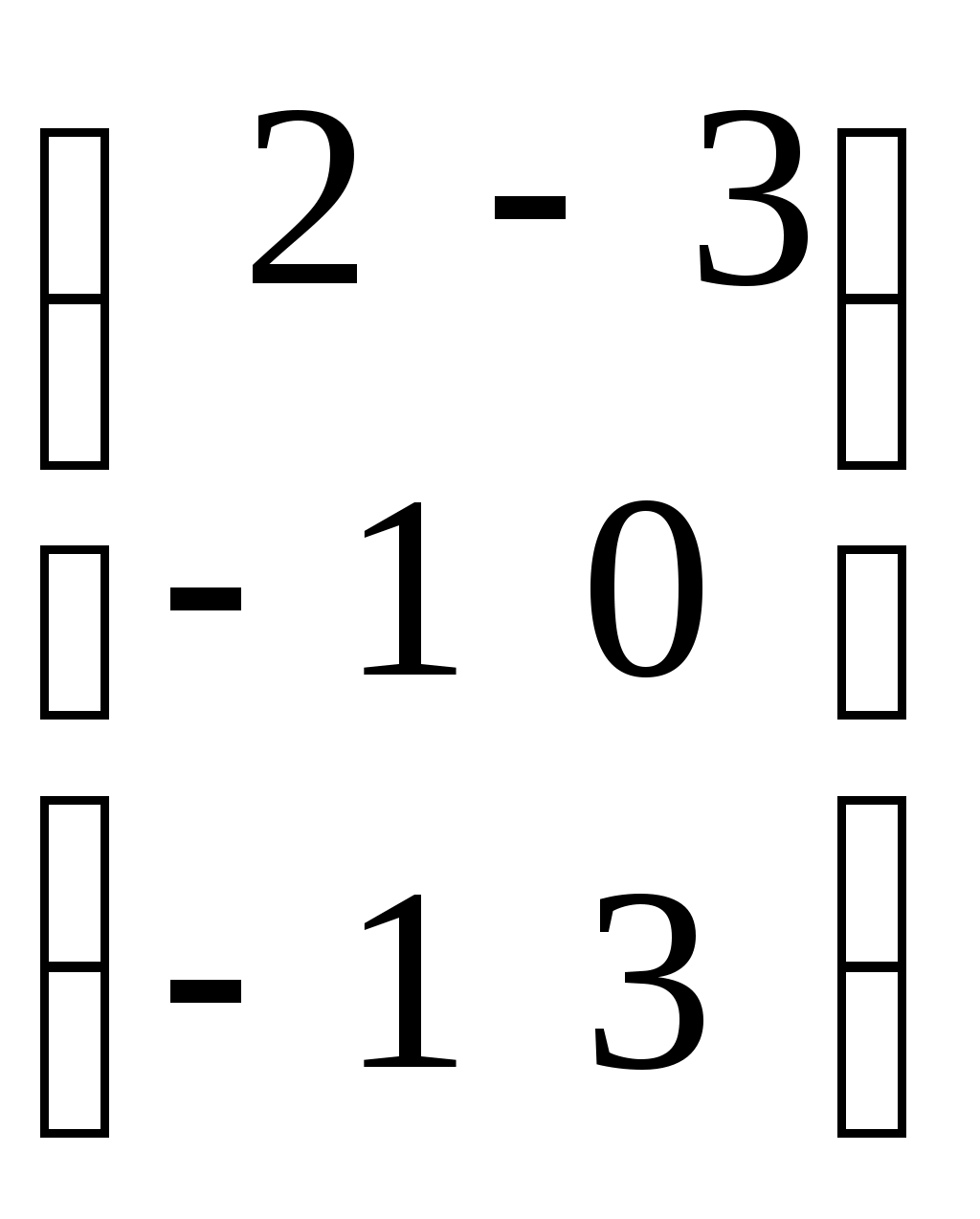
 - матрицы, перестановочные с А = - матрицы, перестановочные с А =  , , 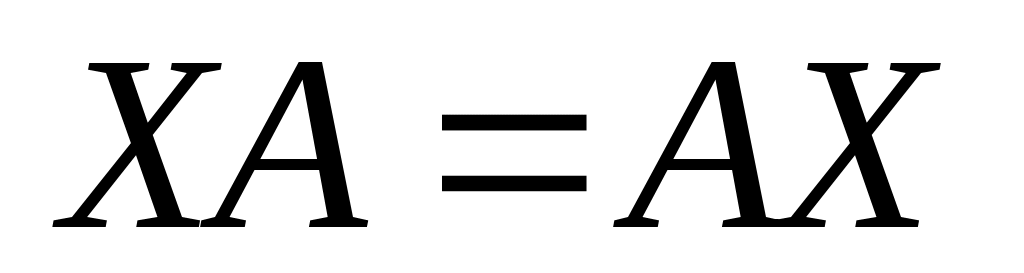
|
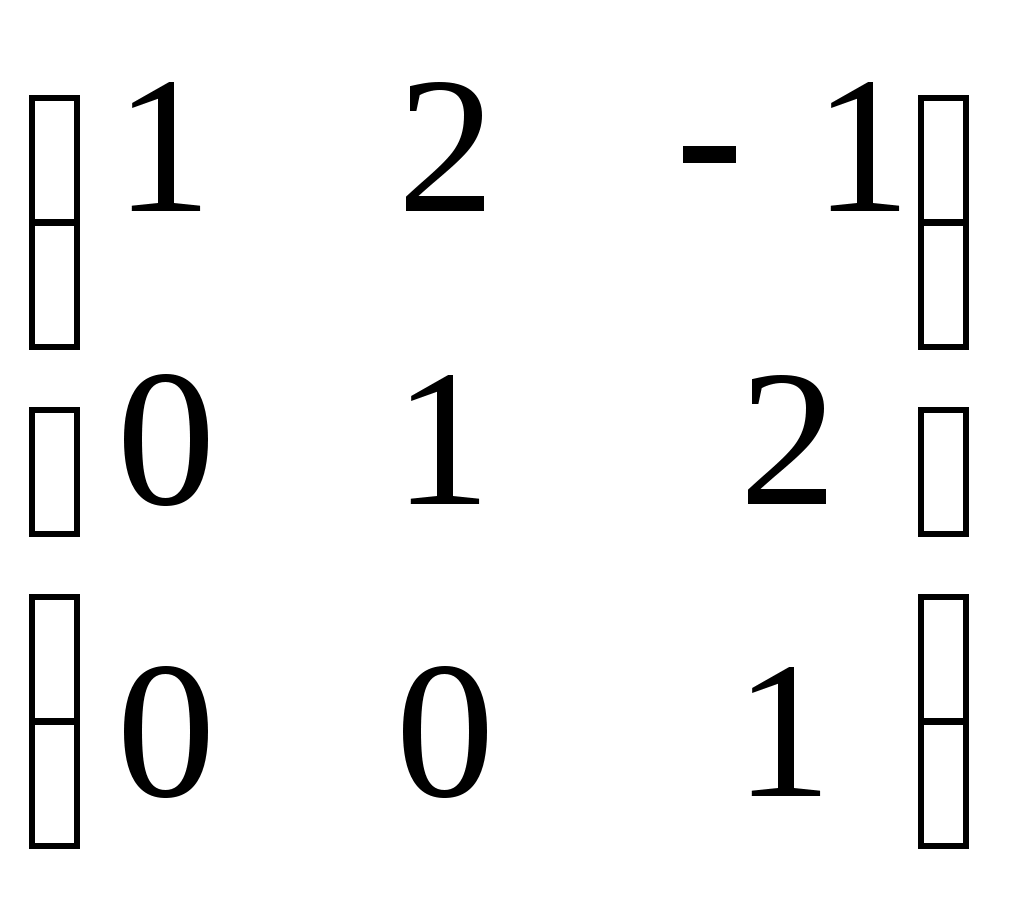
|
4
|
 - матрицы, перестановочные с А = - матрицы, перестановочные с А = 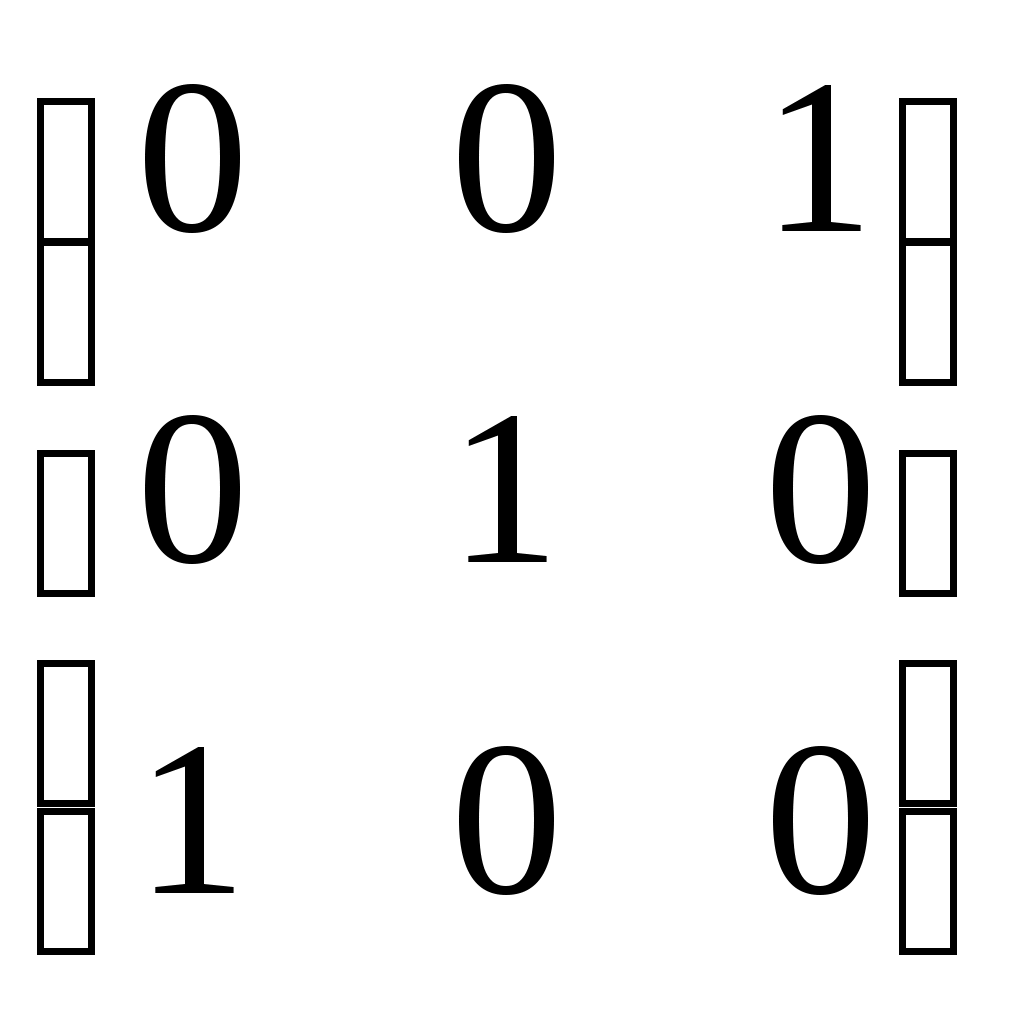 , , 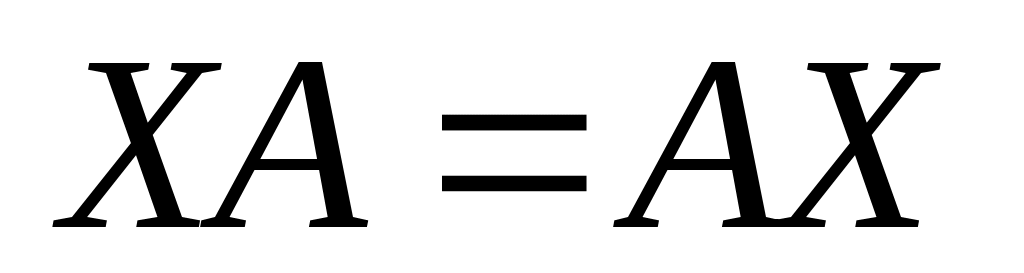
|
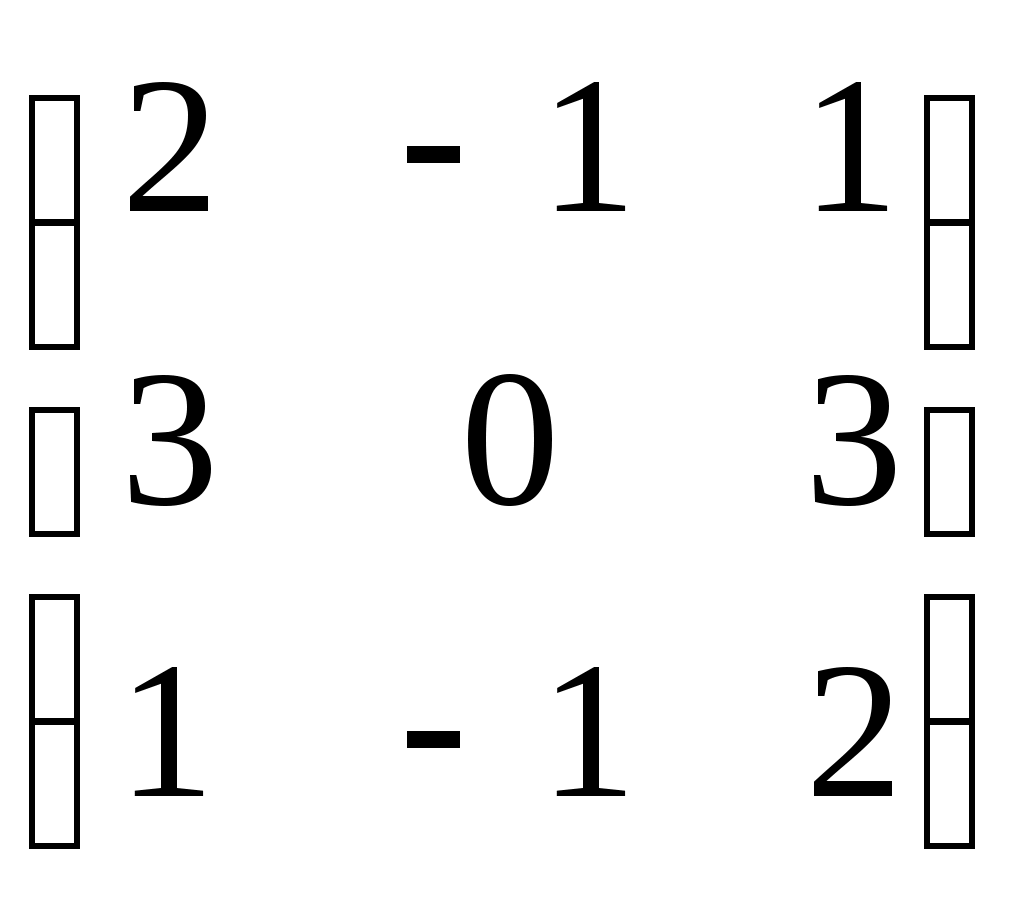
|
5
|
 - матрицы, антиперестановочные с А = - матрицы, антиперестановочные с А = 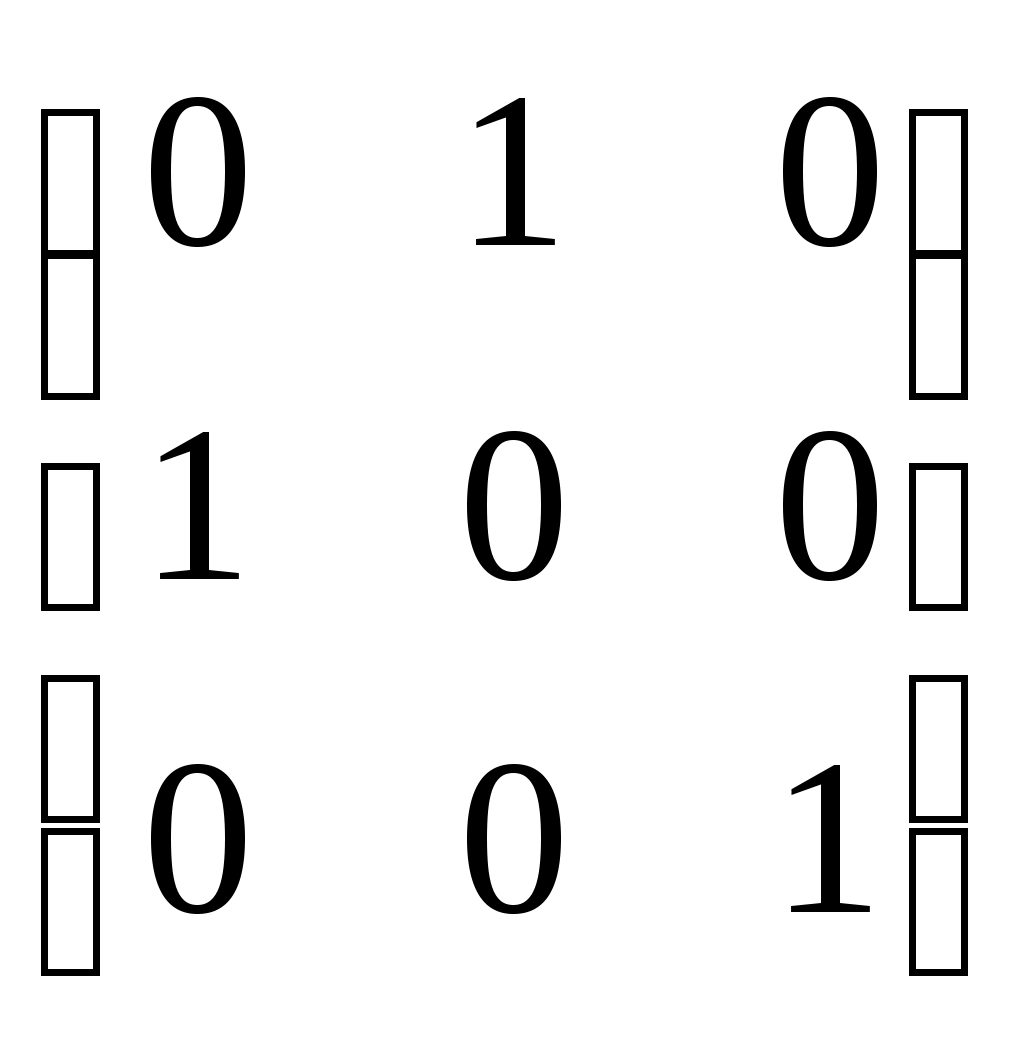 , , 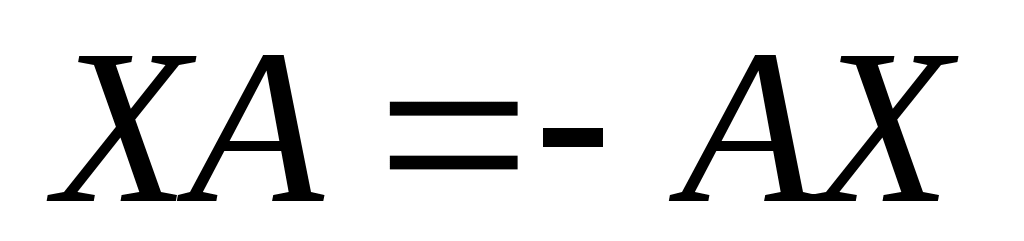
|

|
6
|
 - матрицы, антиперестановочные с - матрицы, антиперестановочные с 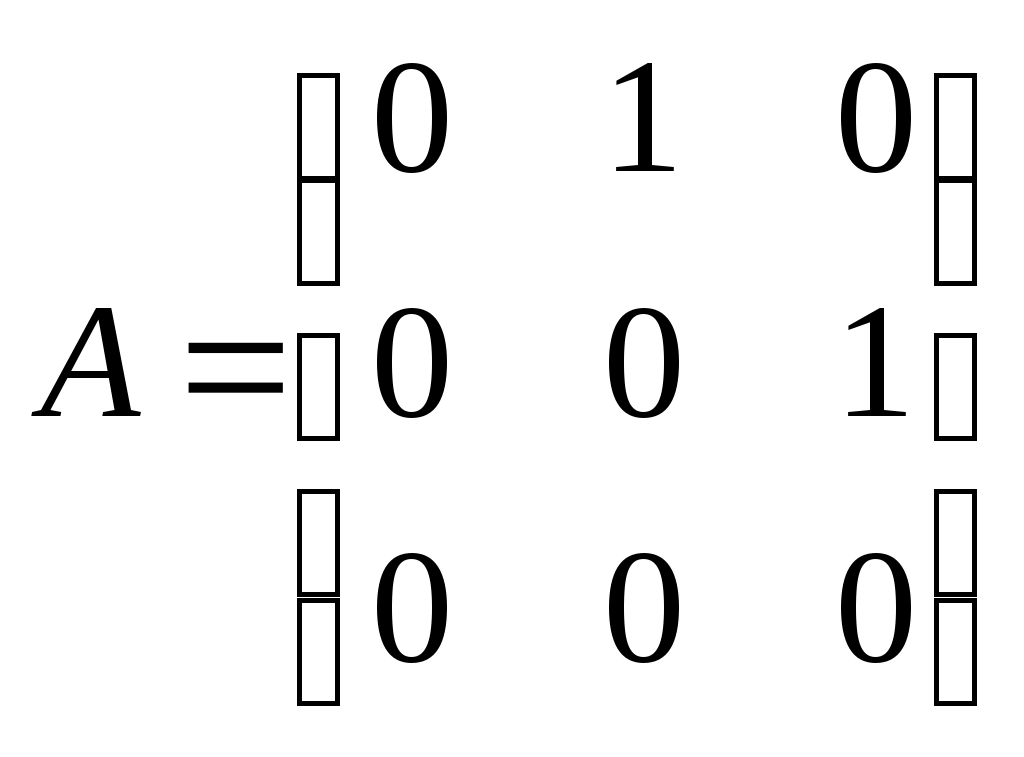 , , 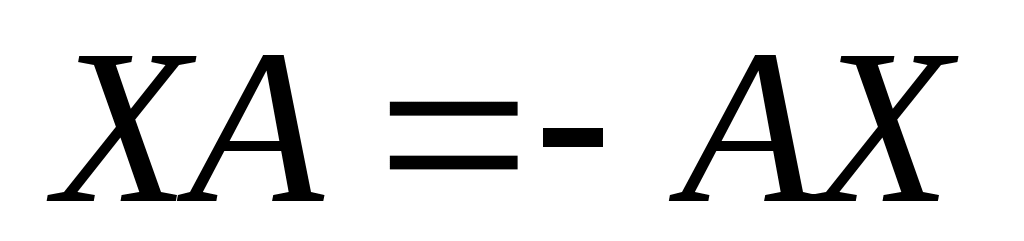
|
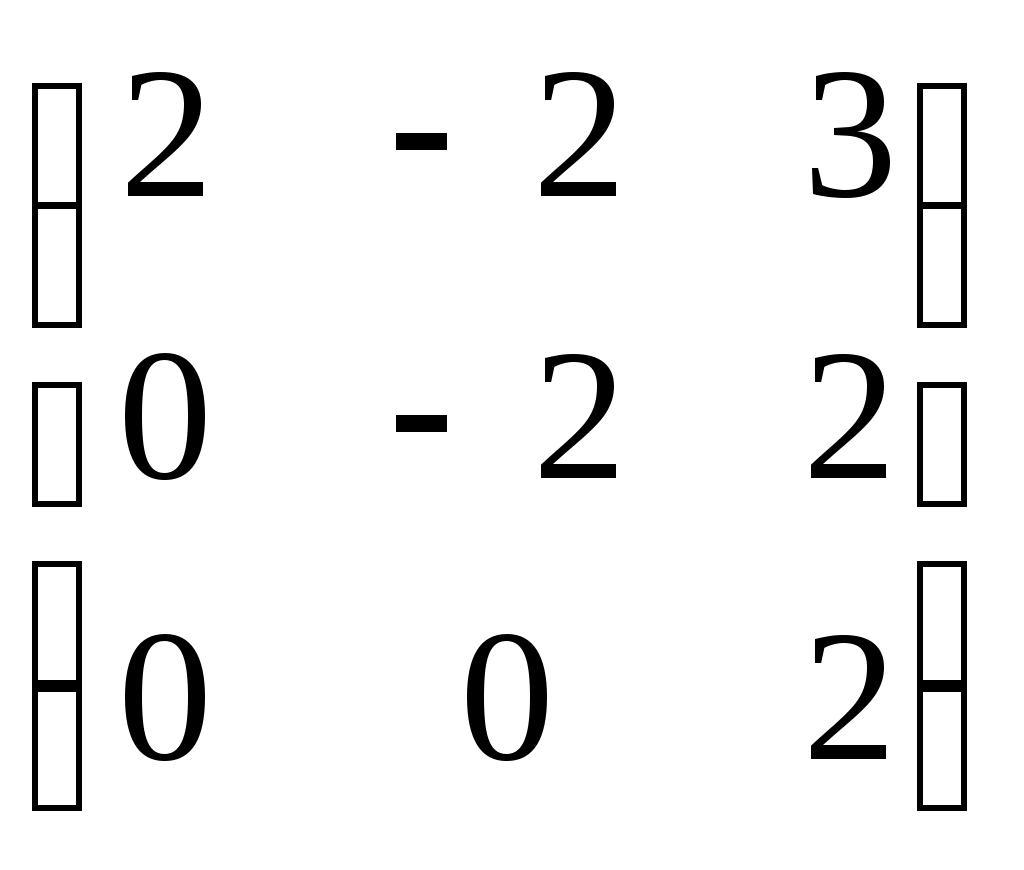
|
7
|
 -симметричные матрицы ( -симметричные матрицы ( ) 3-го порядка, ) 3-го порядка,
|
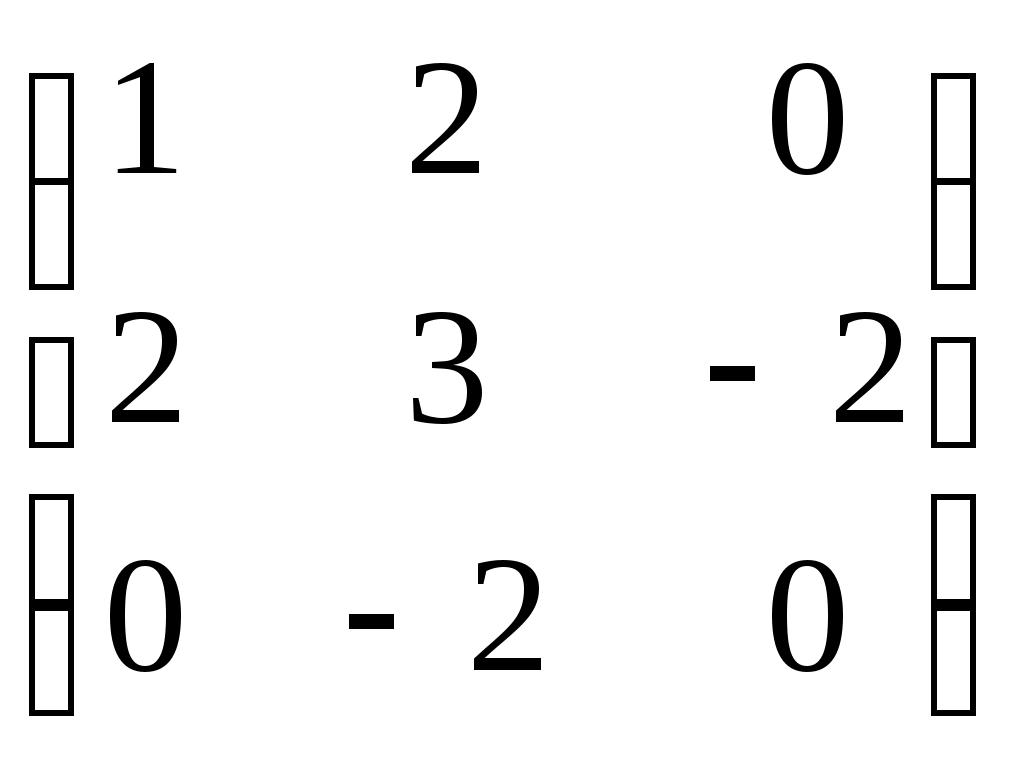
|
8
|
 -кососимметричные матрицы ( -кососимметричные матрицы (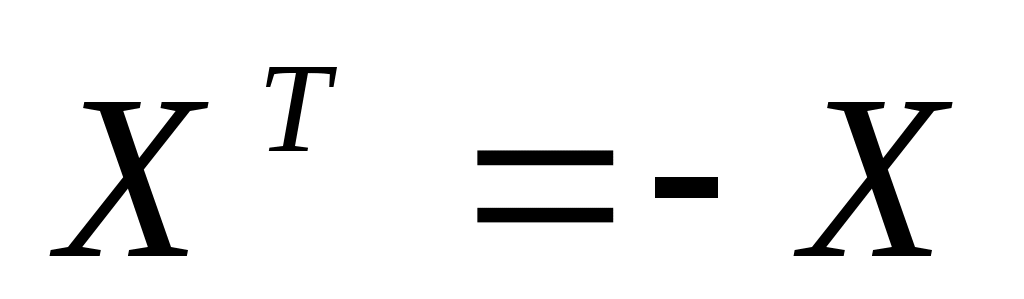 ) 3-го порядка, ) 3-го порядка,
|
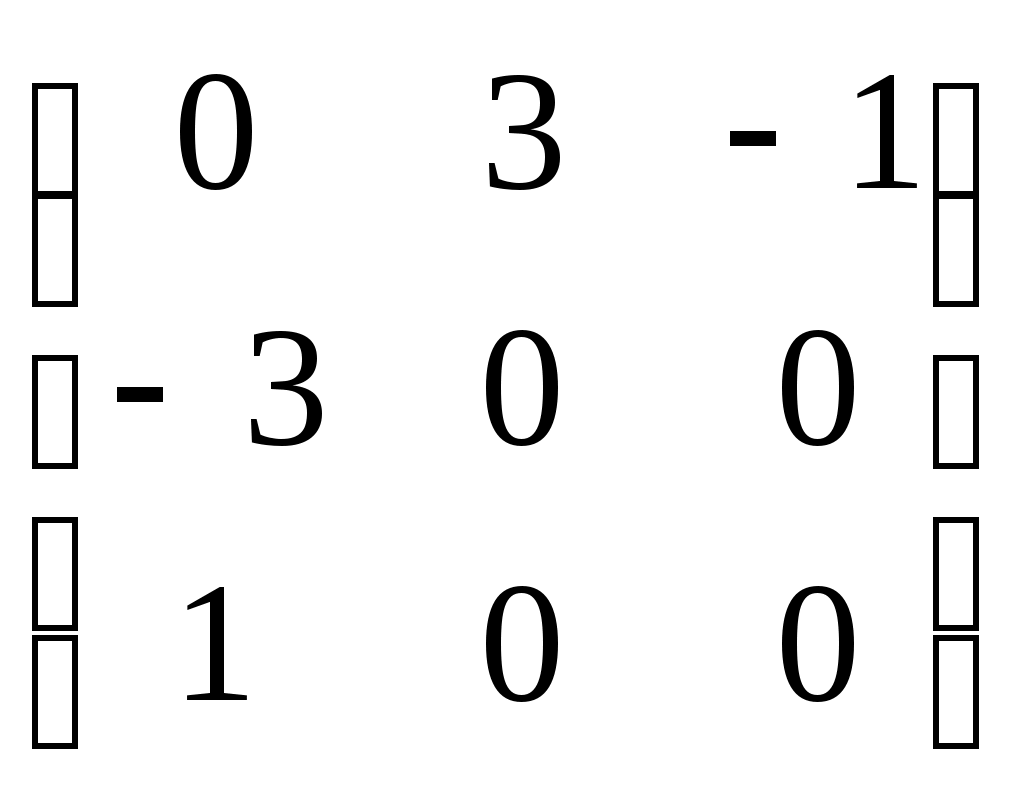
|
9
|
 - верхнетреугольные матрицы 3-го порядка с нулевым следом - верхнетреугольные матрицы 3-го порядка с нулевым следом
(следом называется сумма элементов на главной диагонали)
|
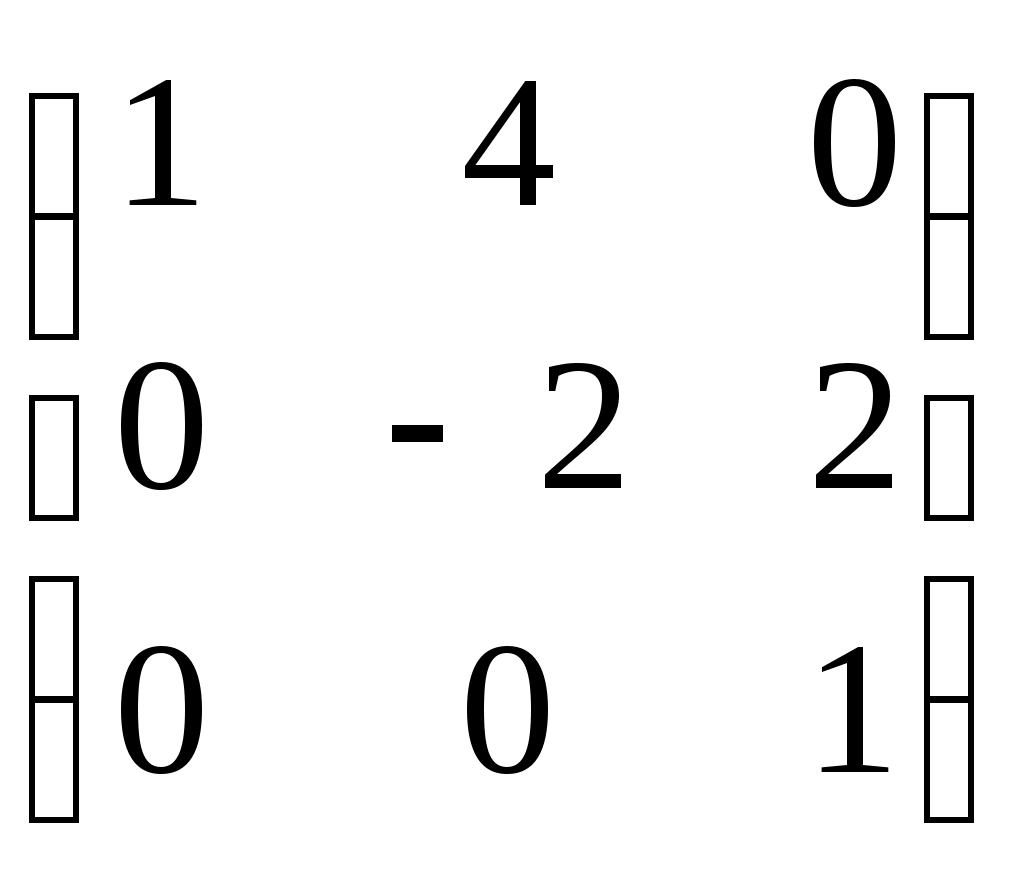
|
10
|
 -матрицы 3-го порядка с нулевыми суммами элементов вдоль главной и побочной диагоналей -матрицы 3-го порядка с нулевыми суммами элементов вдоль главной и побочной диагоналей
|

|
11
|
 -матрицы 3-го порядка, у которых суммы элементов вдоль любой строки и вдоль любого столбца одинаковы -матрицы 3-го порядка, у которых суммы элементов вдоль любой строки и вдоль любого столбца одинаковы
|
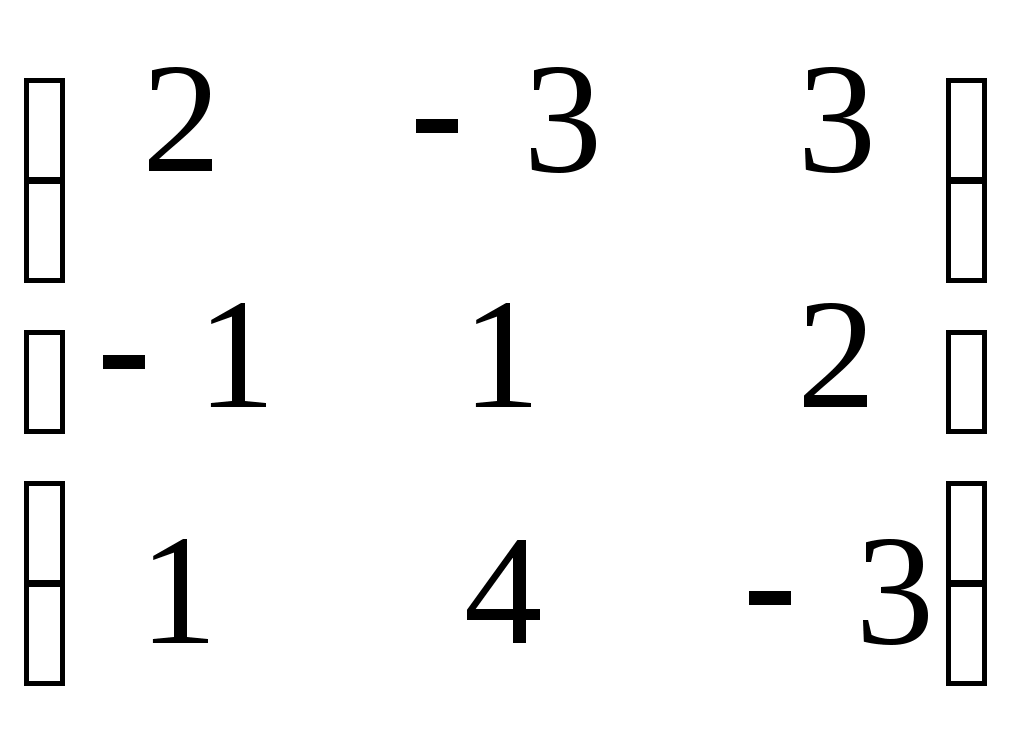
|
12
|
 -матрицы 3-го порядка, у которых суммы элементов вдоль любой строки и вдоль любого столбца равны нулю -матрицы 3-го порядка, у которых суммы элементов вдоль любой строки и вдоль любого столбца равны нулю
|
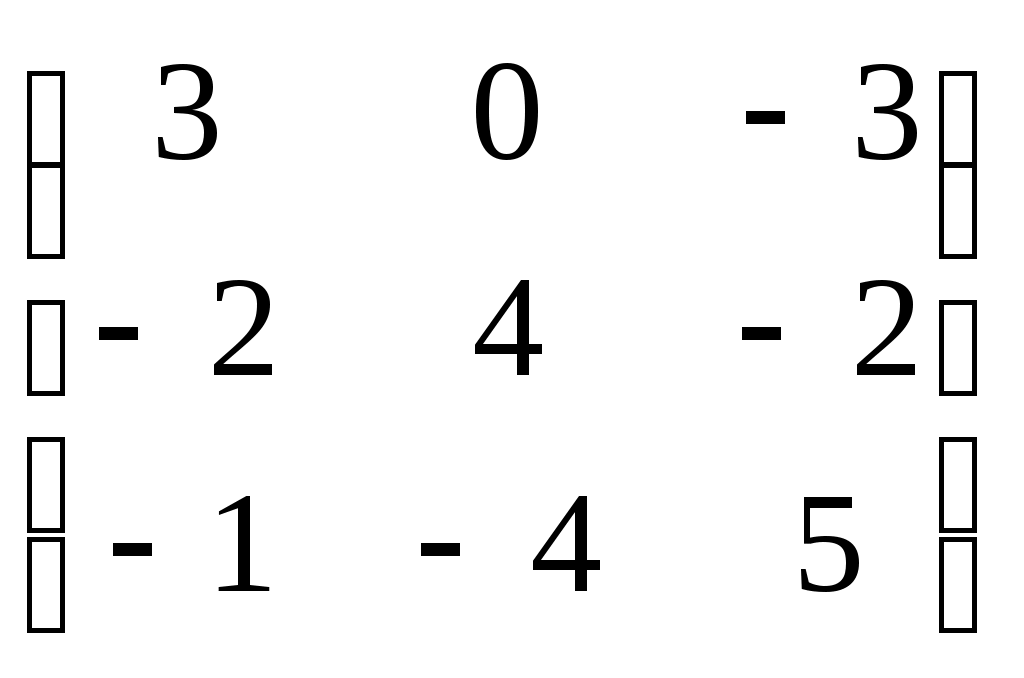
|
13
|
 -матрицы -матрицы 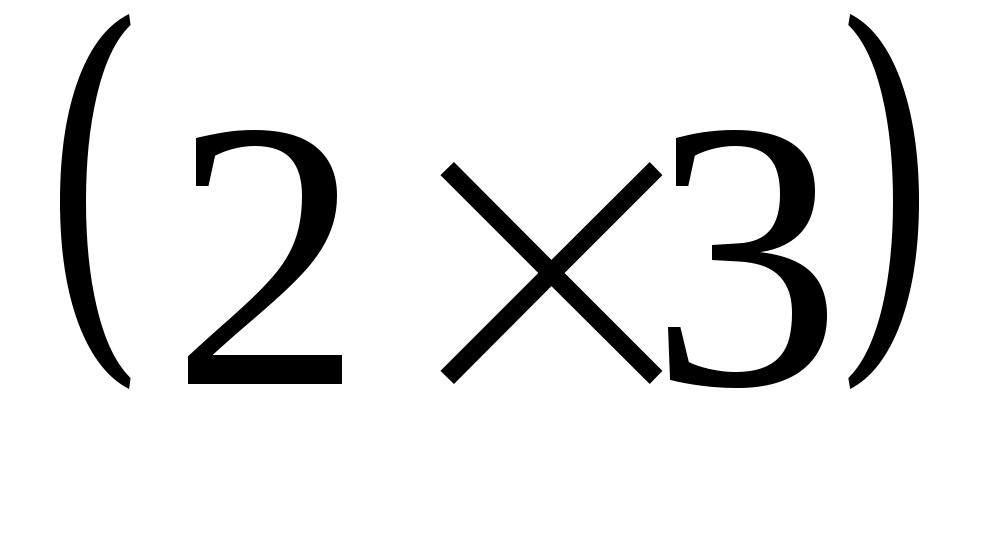 , у которых суммы элементов в обеих строках одинаковы , у которых суммы элементов в обеих строках одинаковы
|
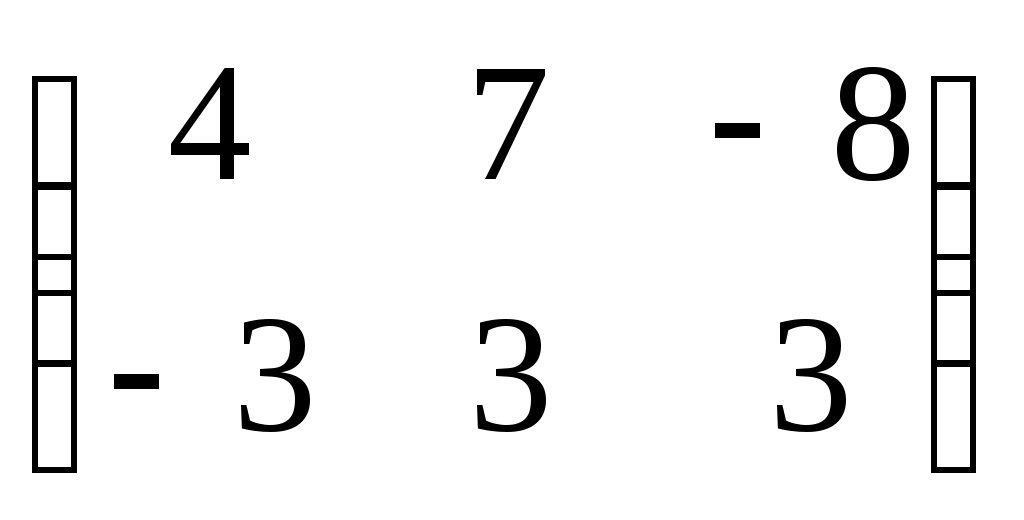
|
14
|
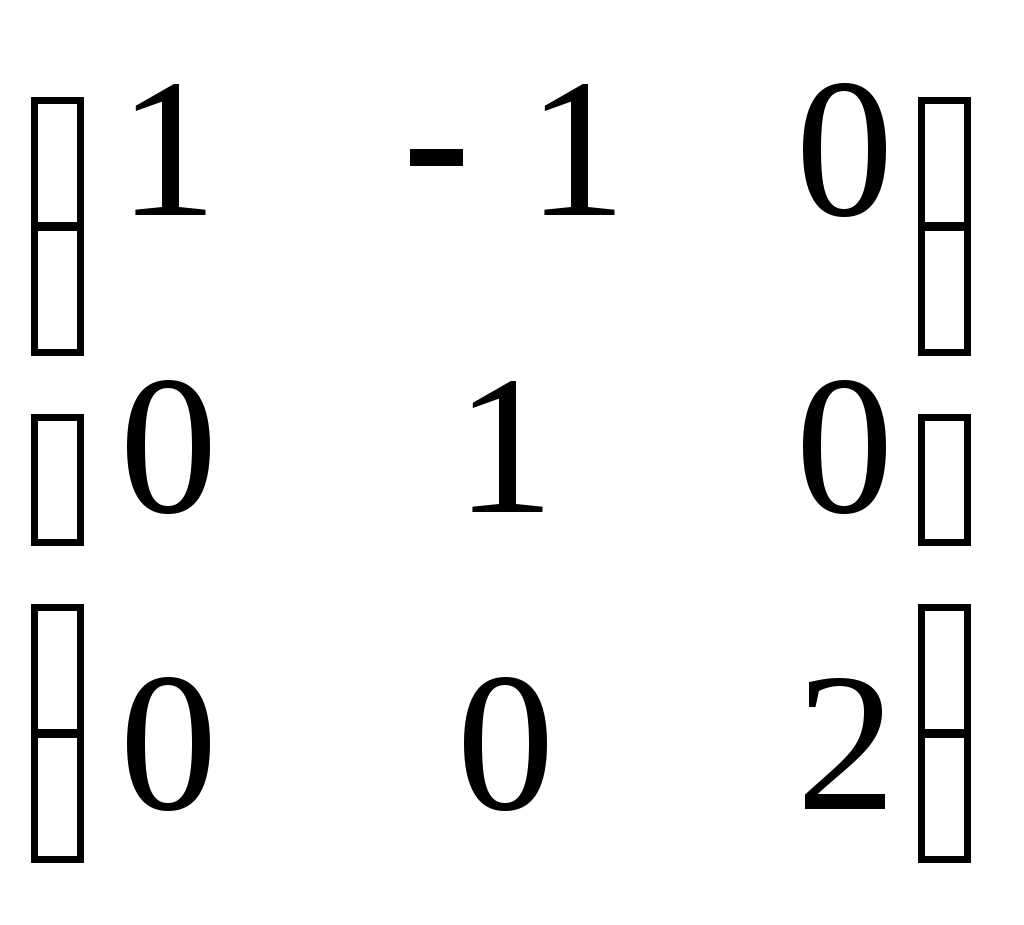
 -матрицы, перестановочные с А = -матрицы, перестановочные с А =  , , 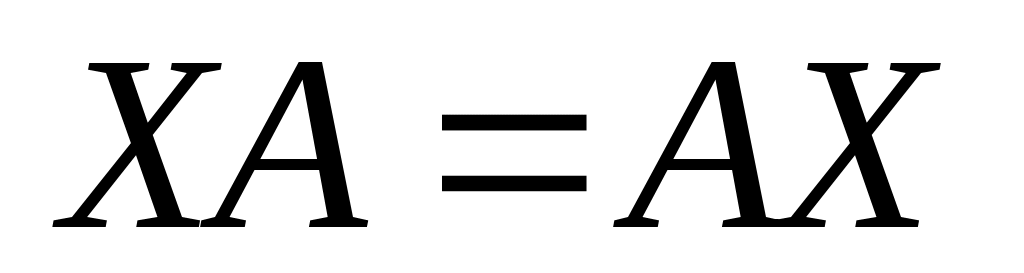
|
|
15
|
 -матрицы, антиперестановочные с А = -матрицы, антиперестановочные с А = 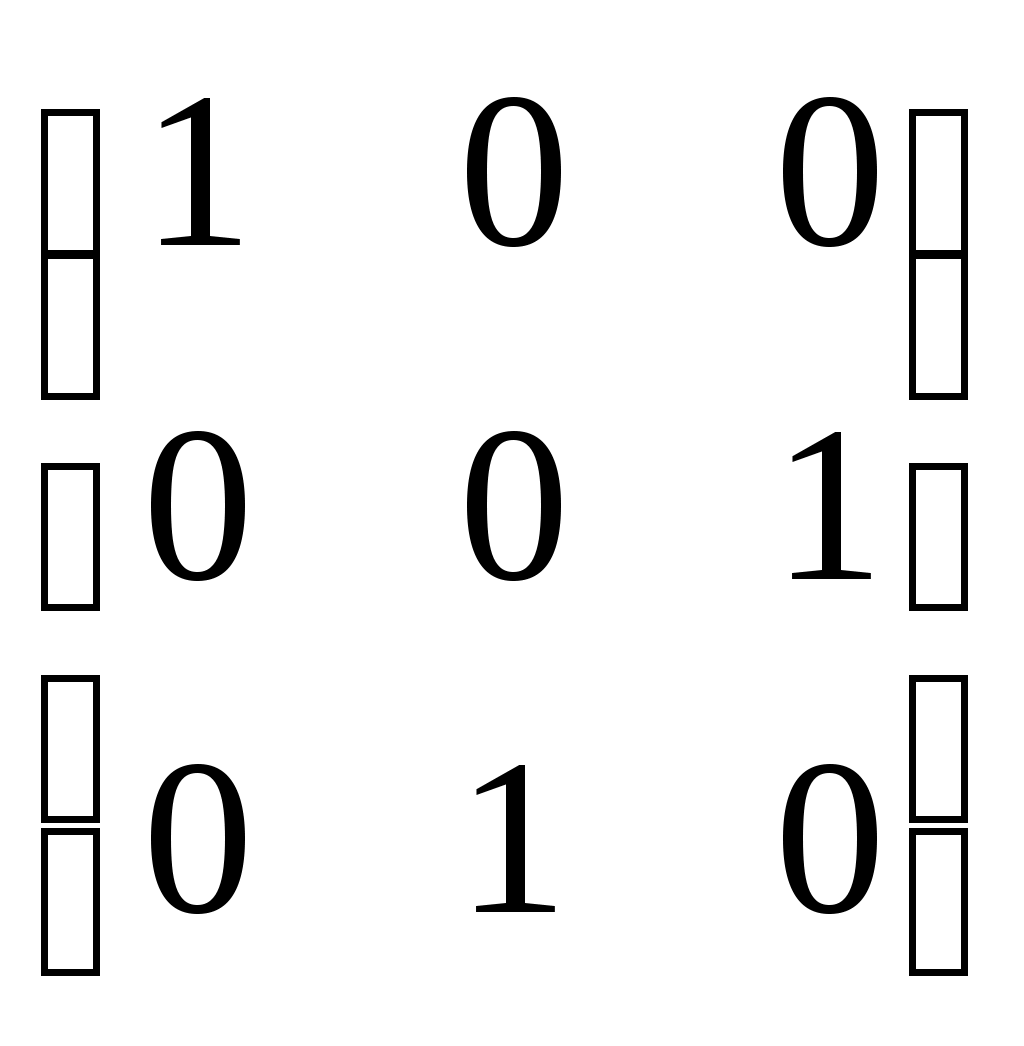 , , 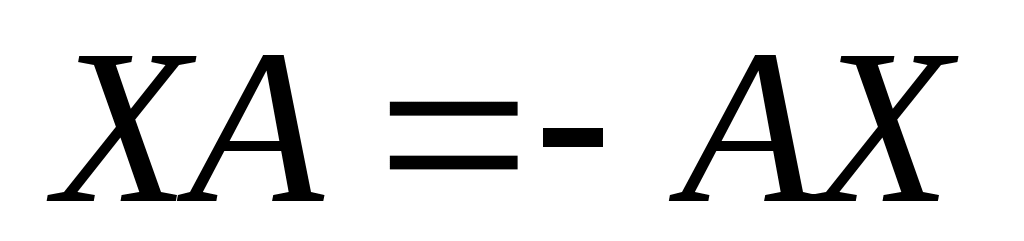
|
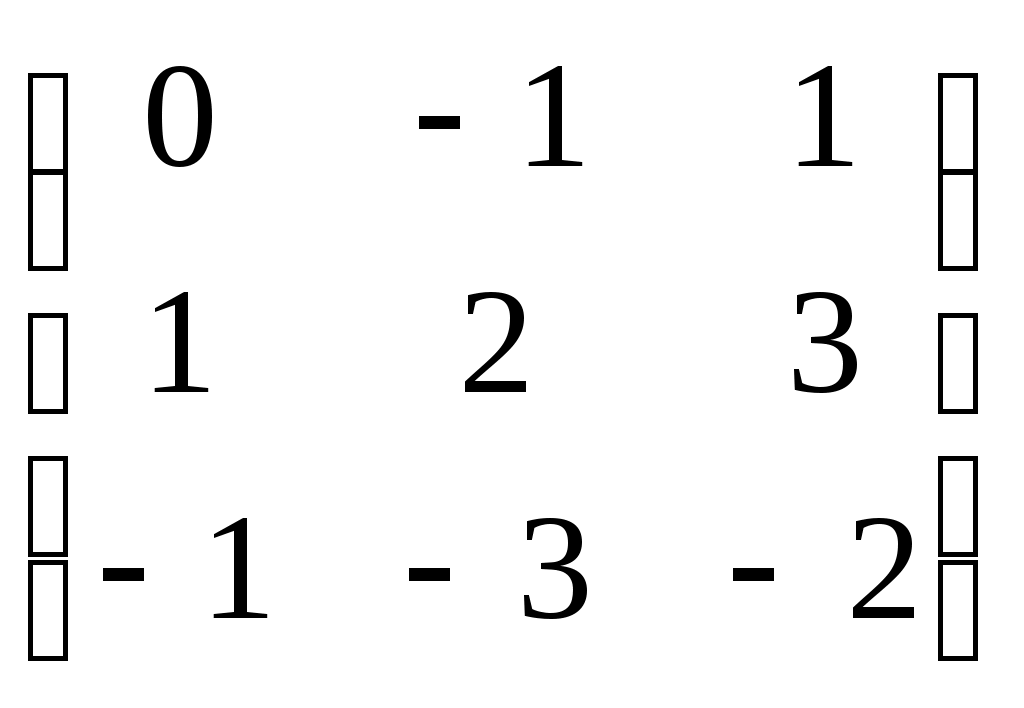
|
16
|
 -решения матричного уравнения -решения матричного уравнения 
|
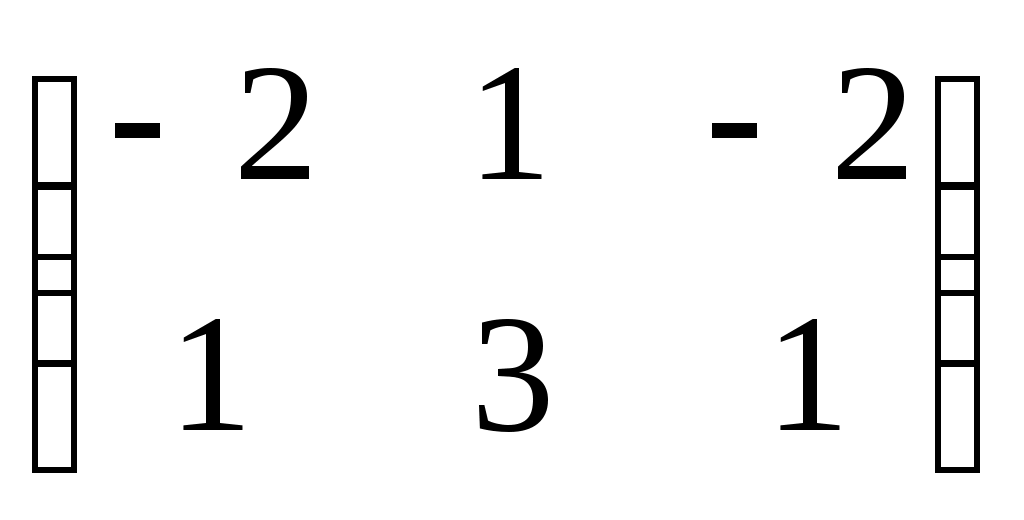
|
17
|
 -решения матричного уравнения -решения матричного уравнения 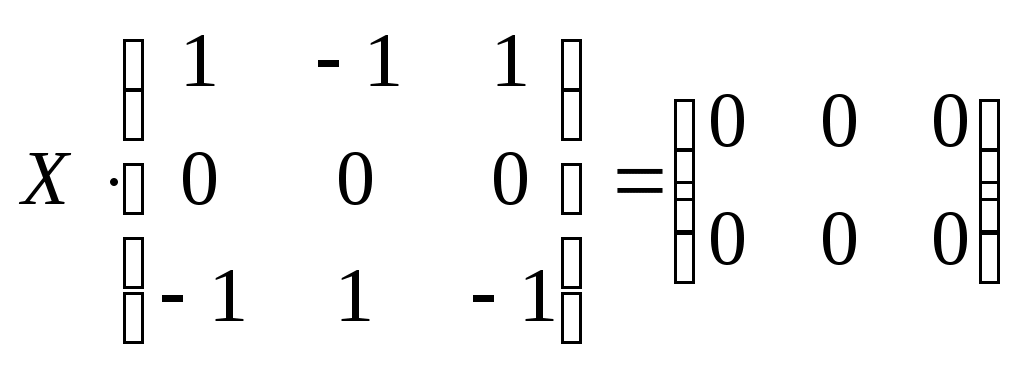
|

|
18
|
 -матрицы, перестановочные с А = -матрицы, перестановочные с А =  , , 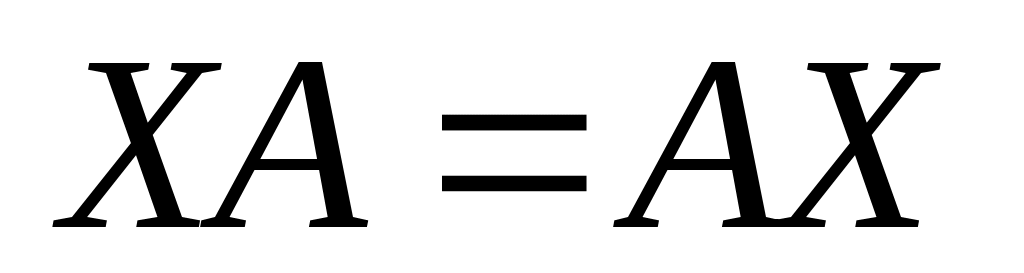
|
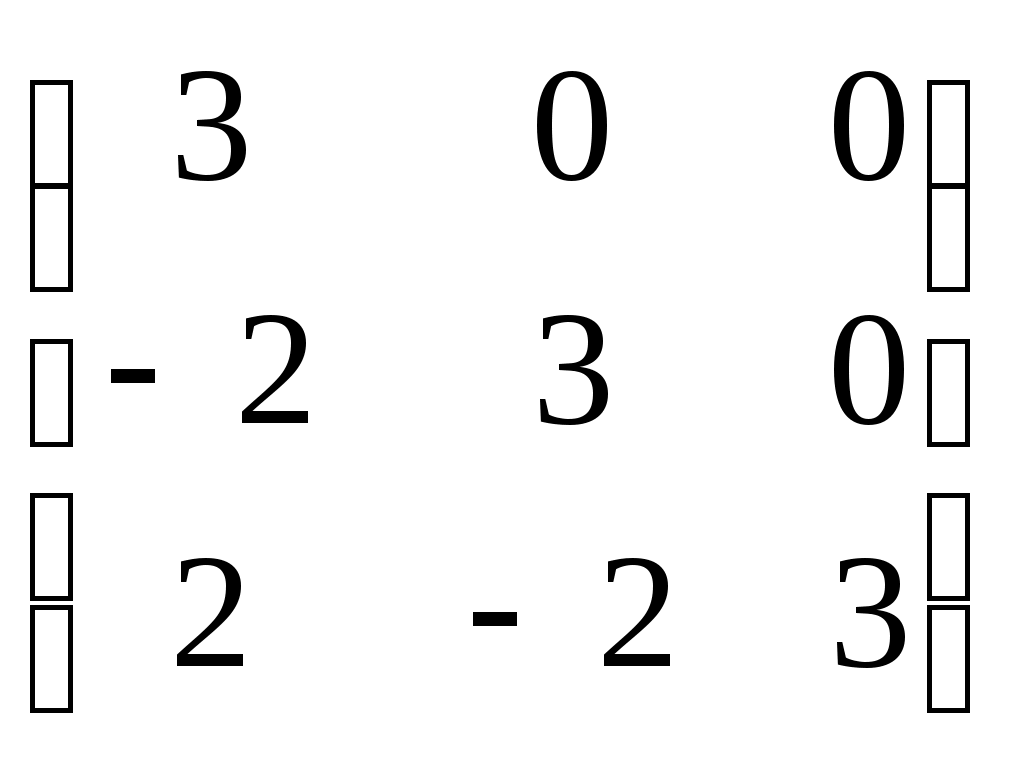
|
19
|
 -матрицы, перестановочные с А = -матрицы, перестановочные с А =  , , 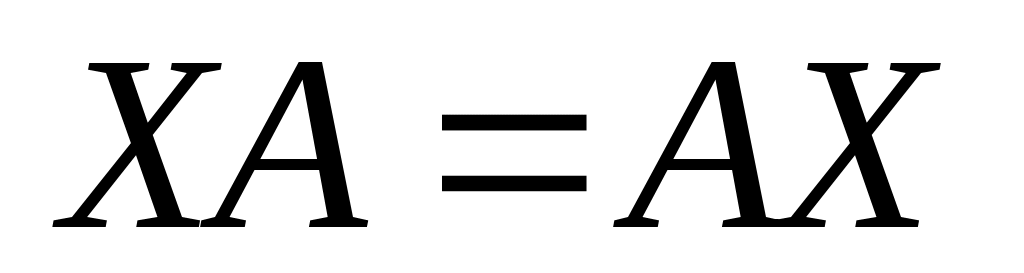
|
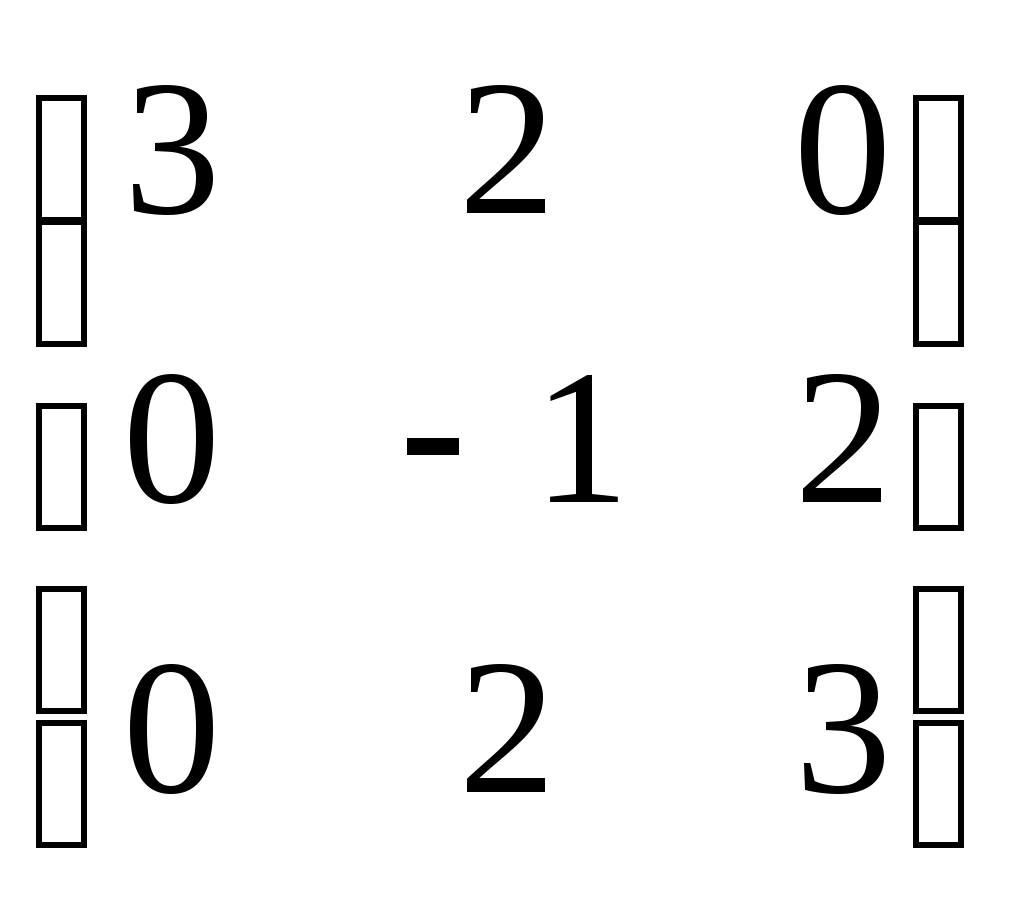
|
20
|
 -матрицы, антиперестановочные с А = -матрицы, антиперестановочные с А =  , , 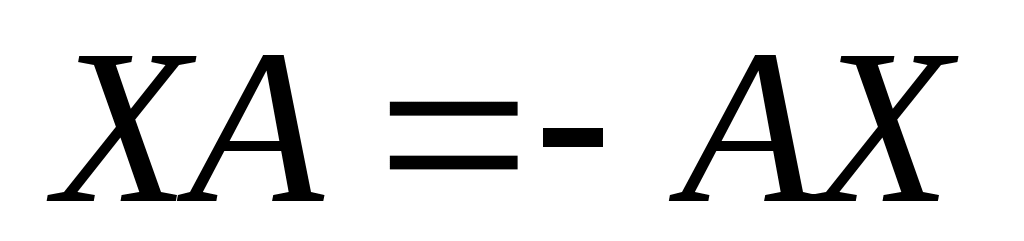
|
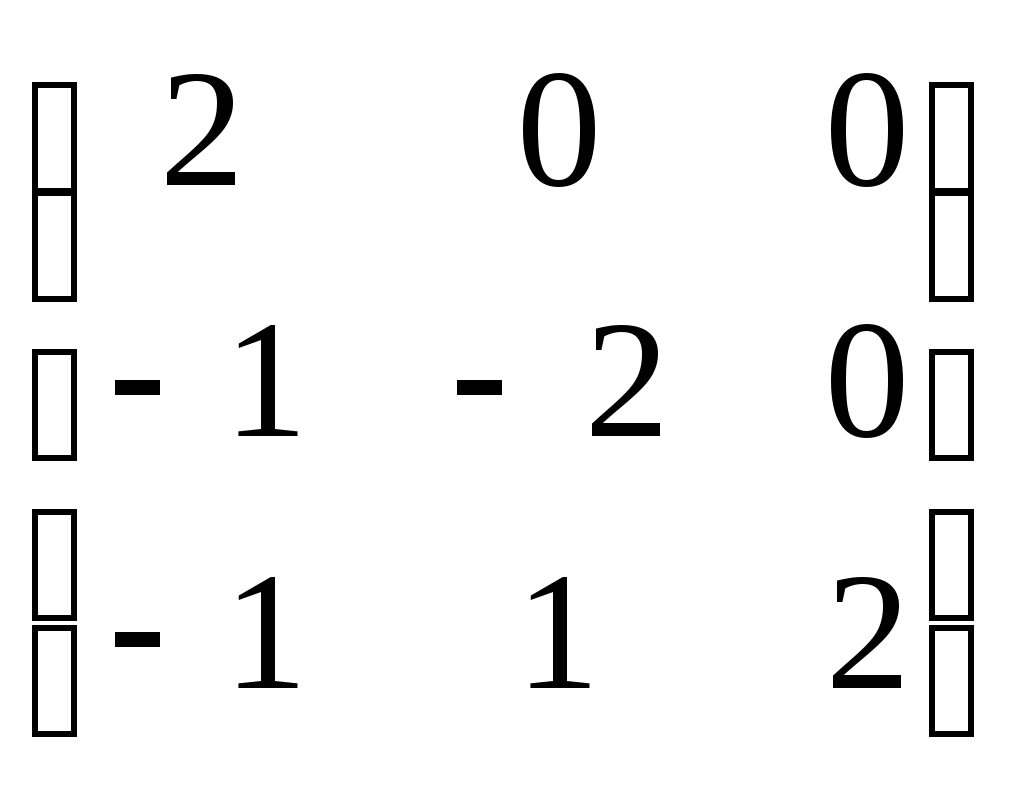
|
21
|
 -матрицы, антиперестановочные с А = -матрицы, антиперестановочные с А =  , , 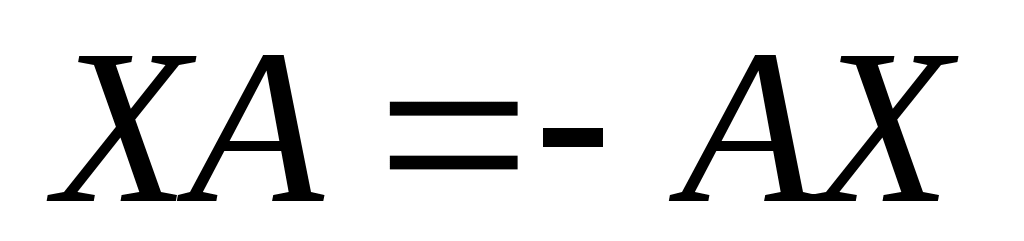
|
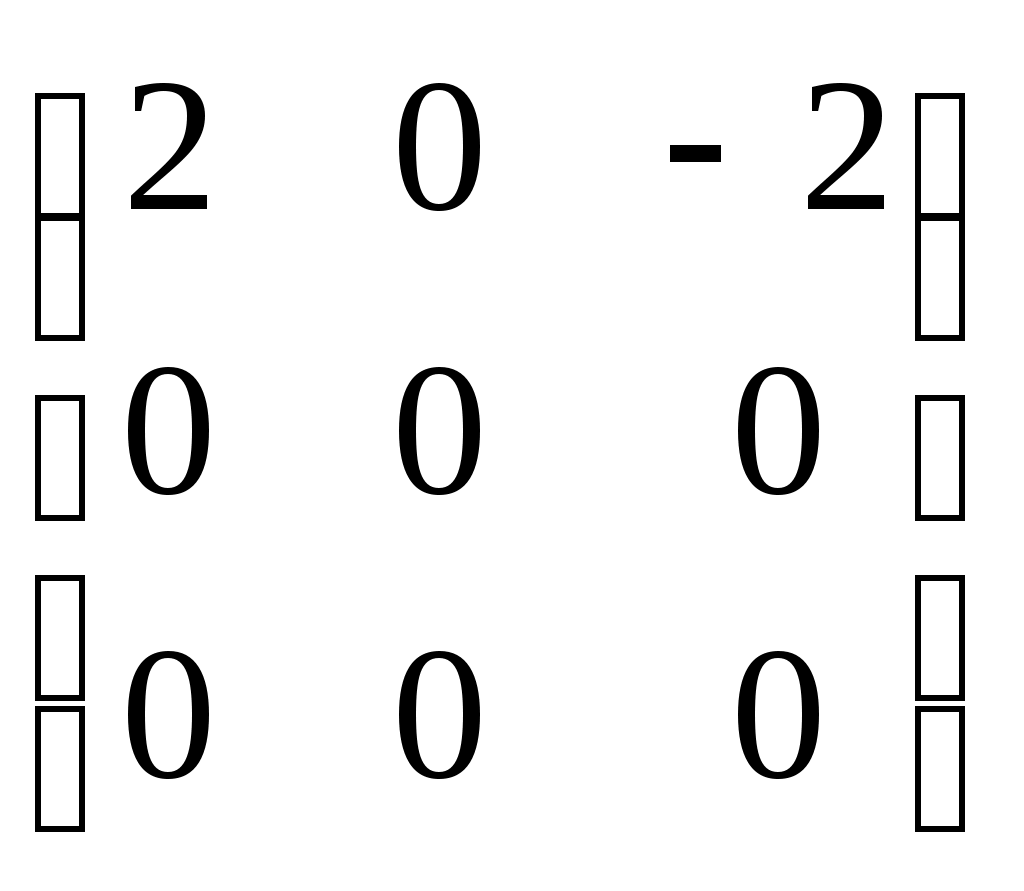
|
22
|
 -симметричные матрицы -симметричные матрицы 3-го порядка с нулевыми суммами элементов из первого и третьего столбцов 3-го порядка с нулевыми суммами элементов из первого и третьего столбцов
|

|
23
|
 -кососимметричные матрицы ( -кососимметричные матрицы (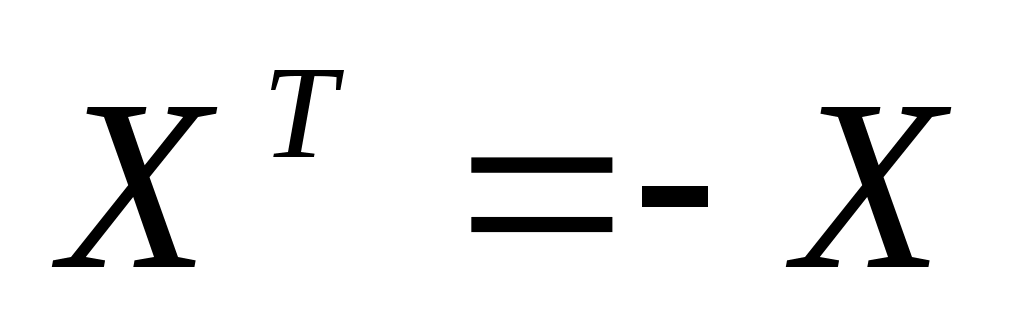 ) 3-го порядка с нулевой суммой элементов из первой строки, ) 3-го порядка с нулевой суммой элементов из первой строки,
|
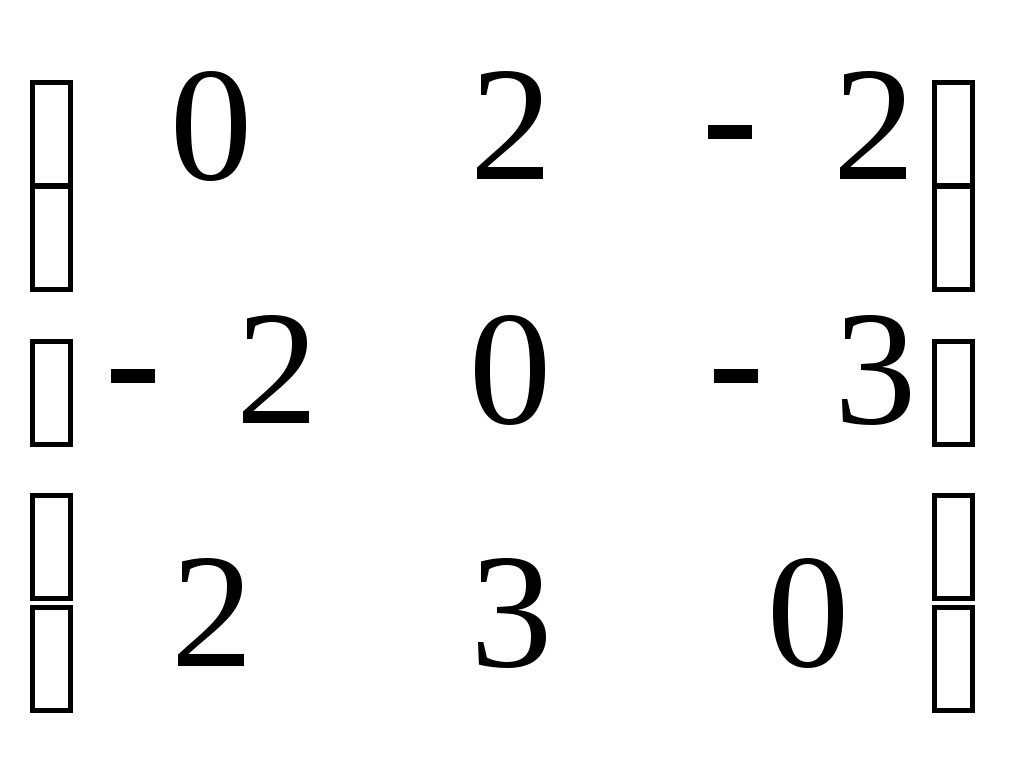
|
24
|
 -нижнетреугольные матрицы 3-го порядка с нулевым следом (следом называется сумма элементов на главной диагонали) и нулевой суммой элементов по побочной диагонали -нижнетреугольные матрицы 3-го порядка с нулевым следом (следом называется сумма элементов на главной диагонали) и нулевой суммой элементов по побочной диагонали
|
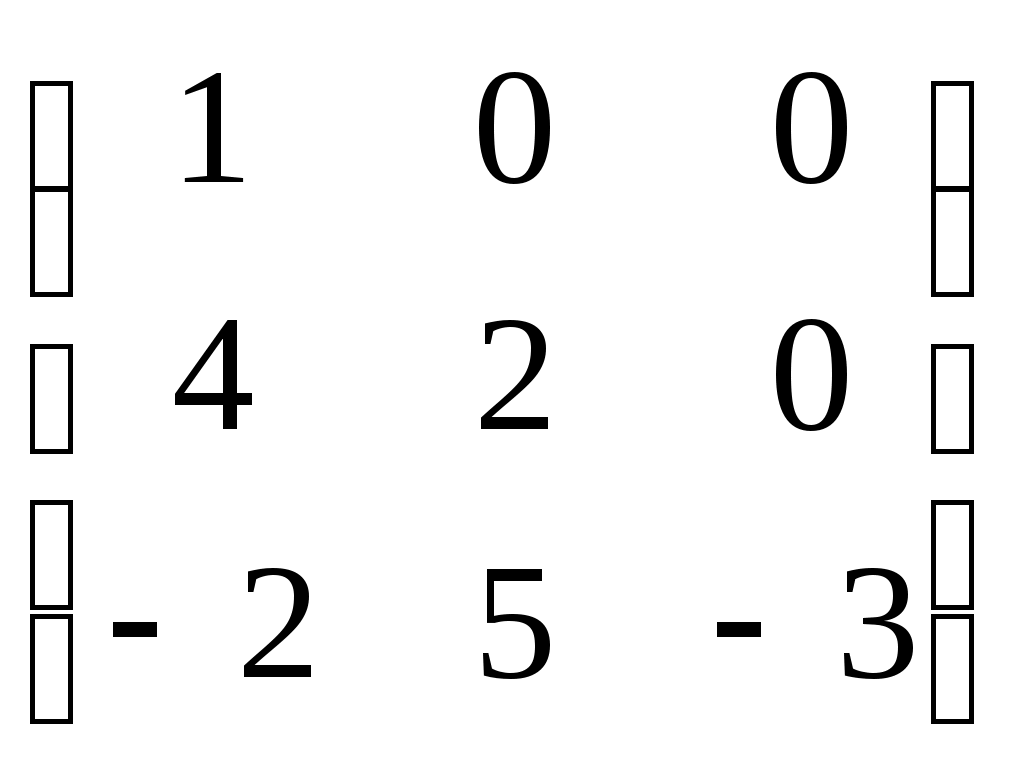
|
25
|
 -симметричные матрицы ( -симметричные матрицы ( ) 3-го порядка, у которых одинаковы суммы элементов в строках, а суммы элементов в столбцах знакочередуются ) 3-го порядка, у которых одинаковы суммы элементов в строках, а суммы элементов в столбцах знакочередуются
|
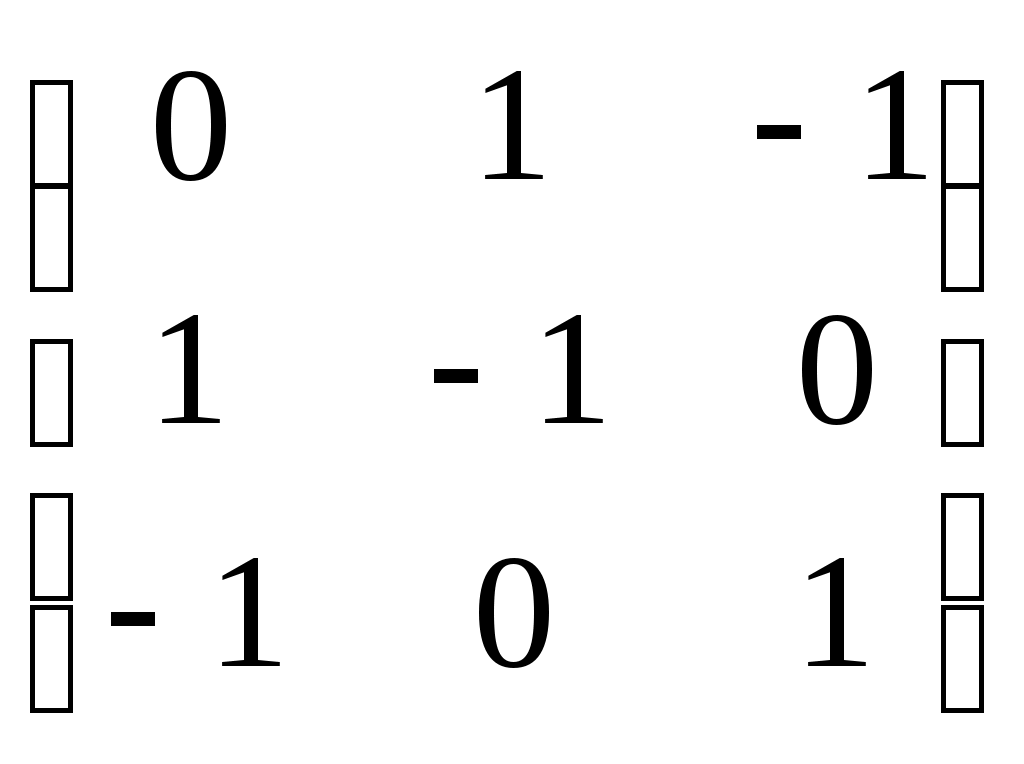
|
26
|
 -симметричные матрицы( -симметричные матрицы( ) 3-го порядка, у которых одинаковы суммы элементов в столбцах, а суммы элементов в строках знакочередуются ) 3-го порядка, у которых одинаковы суммы элементов в столбцах, а суммы элементов в строках знакочередуются
|
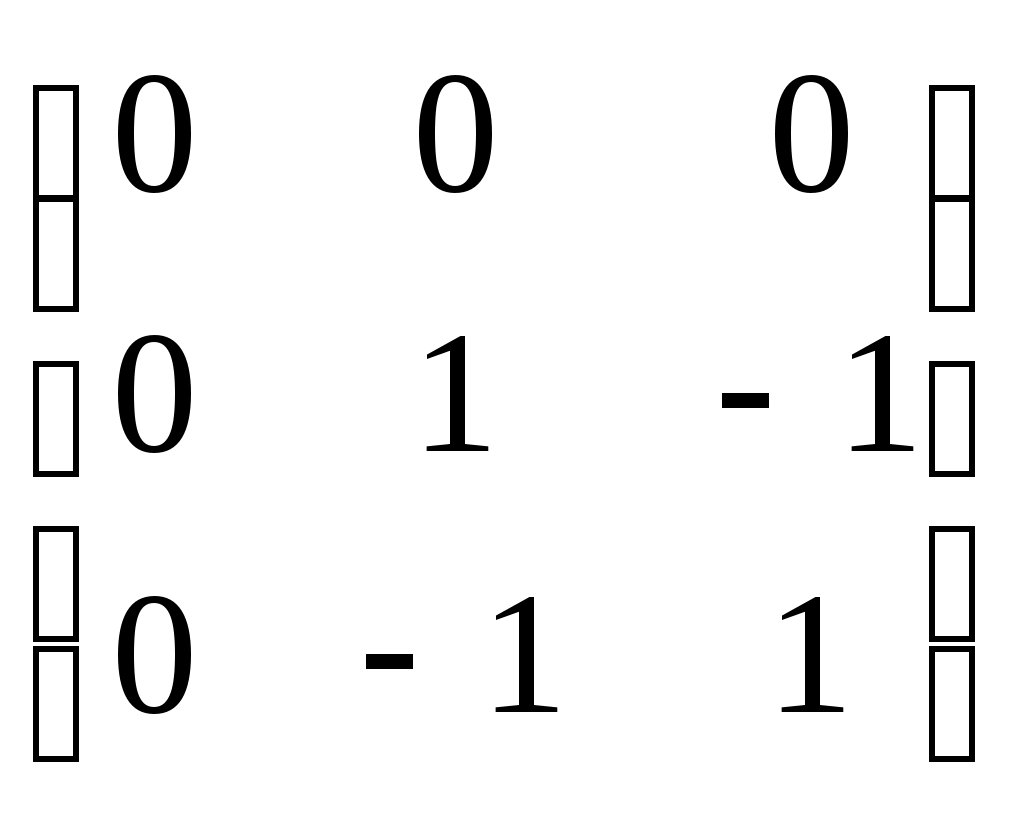
|
27
|
 -симметричные матрицы ( -симметричные матрицы ( ) 3-го порядка, у которых сумма элементов вдоль любого столбца равна 0 ) 3-го порядка, у которых сумма элементов вдоль любого столбца равна 0
|

|
28
|  -матрицы -матрицы 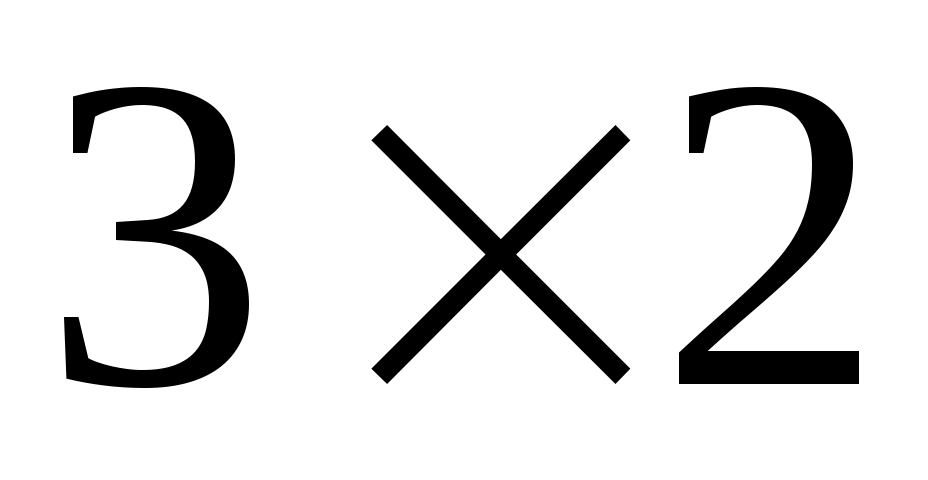 , у которых суммы элементов в обоих столбцах равны 0 , у которых суммы элементов в обоих столбцах равны 0 |
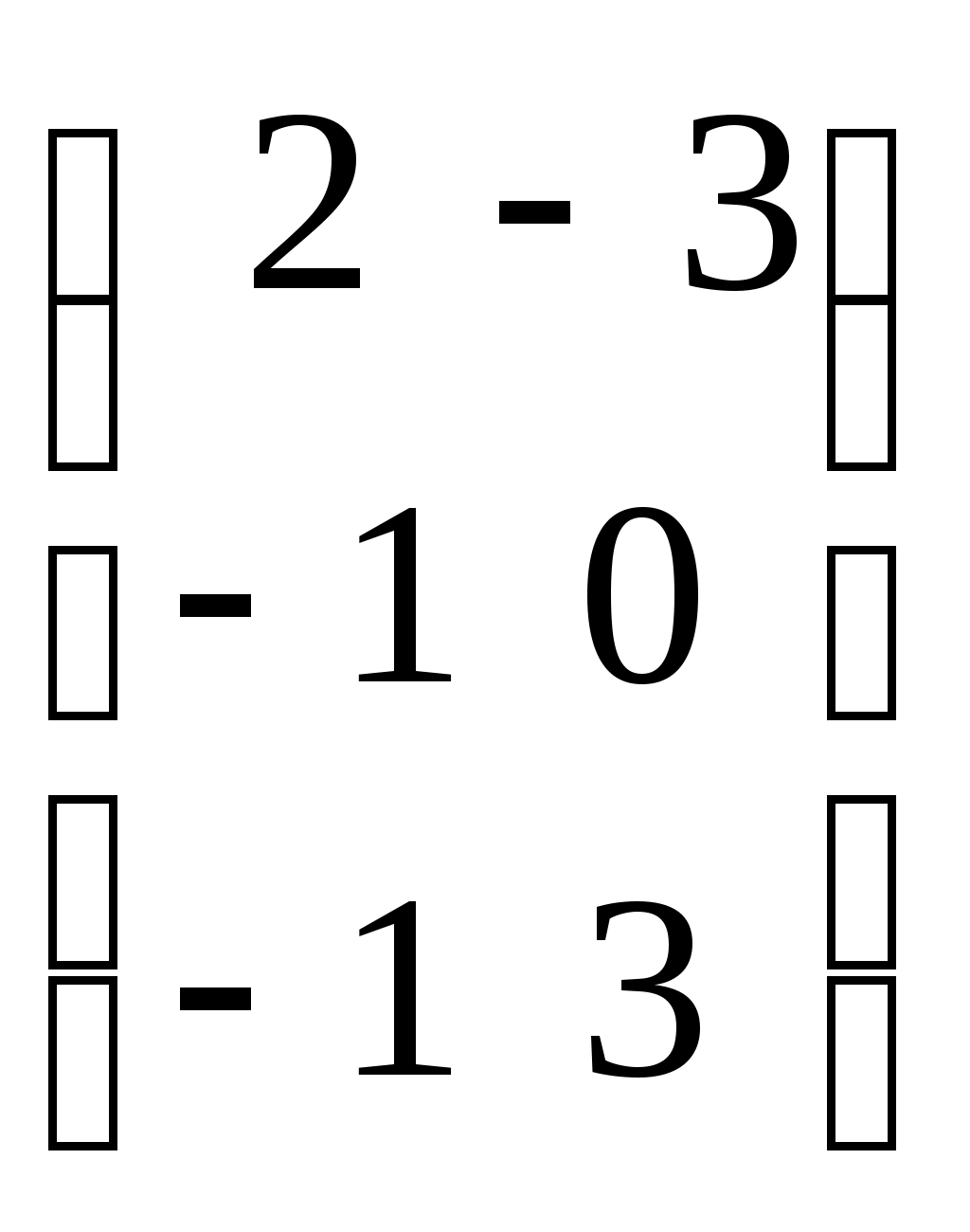
|
29
|
 -симметричные матрицы, перестановочные с матрицей -симметричные матрицы, перестановочные с матрицей
|
А =  , , 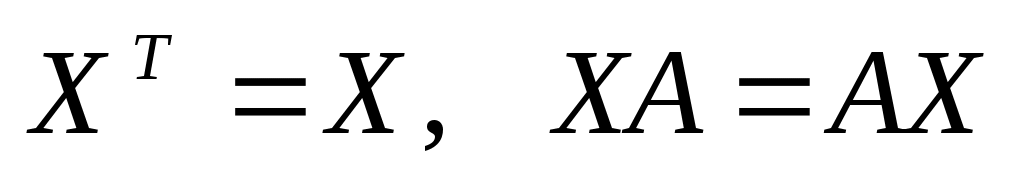
|

|
30
|
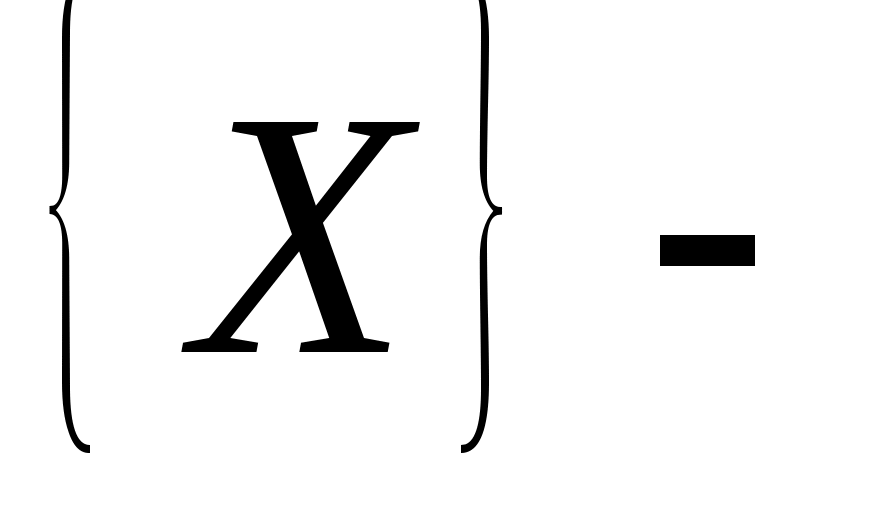 симметричные матрицы, антиперестановочные с матрицей симметричные матрицы, антиперестановочные с матрицей
|
А =  , , 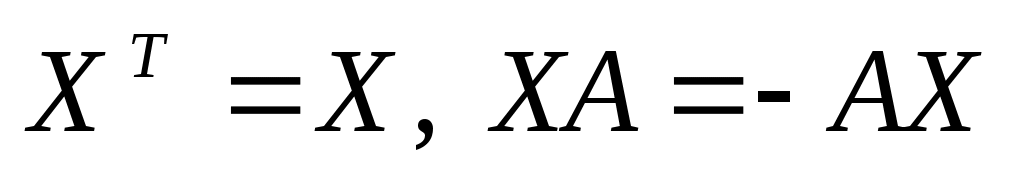
|
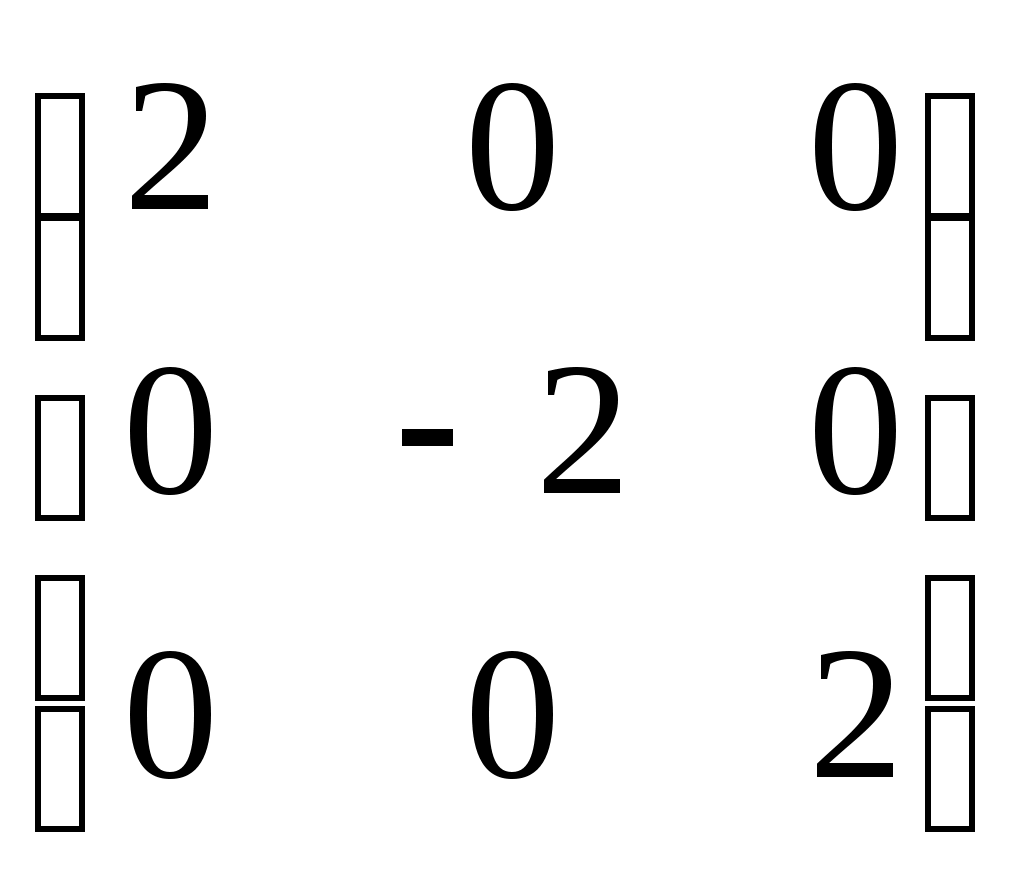
|
 Скачать 1.22 Mb.
Скачать 1.22 Mb.