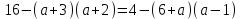|
|
Конспект урока на тему _Тождества_ (7 класс). Тождественные преобразования. Тождественное равенство целых выражений.
Урок № 41
Тема: «Тождественные преобразования. Тождественное равенство целых выражений.»
7б –
7д –
7г –
7и -
Тип урока: ознакомление с новым материалом
Цель урока: ввести понятие тождественного равенства целых выражений; научить доказывать тождества.
Задачи урока:
Предметные: ознакомить и первично закрепить понятия «тождественно равные выражения», «тождество», «тождественные преобразования»; рассмотреть способы доказательства тождеств, способствовать выработке навыков доказательства тождеств.
Личностные: формировать ответственное отношение к обучению, готовность к саморазвитию и самообразованию на основе мотивации к обучению и познанию; формировать навык самостоятельной работы, анализа своей работы и объективной оценки своего труда.
Метапредметные: способствовать развитию наблюдательности, умения анализировать, сравнивать, делать выводы; развивать навыки самоконтроля при выполнении заданий на применение правила вынесения за скобки общего множителя.
Планируемые результаты:
Предметные: доказывают тождества, используя преобразования многочленов.
Личностные: дают позитивную самооценку образовательной деятельности, понимают причины успеха в образовательной деятельности, проявляют познавательный интерес к изучению предмета, к способам решения новых учебных задач.
Метапредметные:
Регулятивные – формируют целевые установки учебной деятельности, выстраивают последовательность необходимых операций (алгоритм действий).
Познавательные – учатся устанавливать аналогии.
Коммуникативные – умеют оформлять свои мысли в устной и письменной речи с учетом речевых ситуаций.
Оборудование: мультимедийный проектор, компьютер, интерактивная доска, карточки
Методы обучения: фронтальный опрос, практическая тренировка, беседа, частично поисковый.
Структура урока:
1.
|
Организационный момент
|
1 мин
|
2.
|
Проверка Д\З
|
3 мин
|
3.
|
Повторение опорного теоретического материала через устный счет
|
8 мин
|
4.
|
Формулирование темы и цели урока
|
2 мин
|
5.
|
Ознакомление с новым материалом
|
7мин
|
6.
|
Физкультминутка
|
2 мин
|
7.
|
Перенос приобретенных знаний и их первичное применение в новых условиях с целью формирования умений
|
13 мин
|
6.
|
Рефлексия
|
2 мин
|
7.
|
Постановка Д/З
|
2 мин
|
Ход урока
Учитель
|
Ученики
|
УУД
|
Организационный момент
|
|
Приветствую учащихся. Сажаю их на места.
|
Приветствуют учителя.
|
К: следовать правилам поведения
|
Проверка Д/З
|
|
- Какие вопросы по Д/З? Разбираем, если есть вопросы.
|
Спрашивают.
|
К: оформлять свои мысли в устной форме
|
Повторение опорного теоретического материала через устный счет
|
|
(слайд 1, 2)
Решить уравнение (по вариантам).
1) (2х + 1)² = 13 + 4х²
2) (3х - 1)² - 9х² = - 35
Решение:
решение
4х² + 4х + 1 = 13 + 4х²
4х² + 4х - 4х² = - 1 + 13
4х = 12
х = 3
Ответ: 3
2) решение
9х² - 6х + 1 - 9х² = -35
-6х = - 1 – 35
- 6х = - 36
х = 6
Ответ: 6
(слайд 3-4)
Выполните действия:
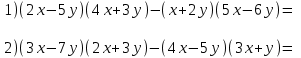
Решение:
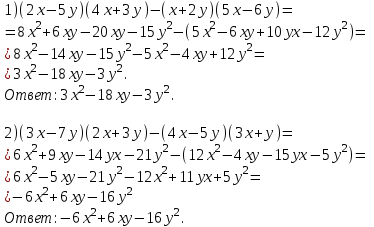
- Мы с вами решили уравнение. Преобразовали выражение. А какие преобразования называются тождественными?
- Как вы думаете, чем мы будем заниматься сегодня на уроке?
– Какова тема урока?
|
Разбираем вместе, один ученик у доски, остальные в тетрадях
выполняют самостоятельно, с последующей взаимопроверкой
|
П: уметь ориентироваться в своей системе знаний
К: уметь слушать и понимать речь других, оформлять мысли в устной речи
Р: уметь проговаривать последовательность действий на уроке, высказывать свое предположение
|
4. Формулирование темы и цели урока
|
Сформулируйте тему и задачи урока. Запишите ее в тетрадях.
(слайд 5)
Сегодня на уроке я хочу:
Узнать…
Применить …
Оценить …
-
|
Слушают.
Записывают.
отвечают
|
|
5. Ознакомление с новым материалом
|
Задание 1.
Найдем значение выражений при х=5 и у=4
3(х+у)=3(5+4)=3*9=27
3х+3у=3*5+3*4=27
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных значения выражений 3(х+у) и 3х+3у равны.
Задание 2.
Рассмотрим теперь выражения 2х+у и 2ху. При х=1 и у=2 они принимают равные значения:
2х+у=2*1+2=4
2ху=2*1*2=4
Однако можно указать такие значения х и у, при которых значения этих выражений не равны. Например, если х=3, у=4, то
2х+у=2*3+4=10
2ху=2*3*4=24
- Как вы думаете, какие выражения называются тождественно равными?
(слайд 6)
Определение: Два выражения, значения которых равны при любых значениях переменных, называются тождественно равными.
Определение: Равенство, верное при любых значениях переменных, называется тождеством.
Левую и правую части тождества называют выражениями, тождественно равными друг другу (или тождественными).
Определение: Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения.
Выражения 3(х+у) и 3х+3у являются тождественно равными, а выражения 2х+у и 2ху не являются тождественно равными. Почему?
(слайд 7)
Примеры тождеств:
a+b = b+a
a+(b+c) = (a+b)+c
ab = ba
a(bc) = (ab)c
a(b+c) = ab+ac
a+0 = a
a∙0 = 0
a∙1 = a
a∙(-1) = -a
(слайд 8)
Способы доказательства тождеств
Преобразование левой части тождества так, чтобы получилась её правая часть
(если после преобразования левой части, выражение получится как в правой части , то данное выражение является тождеством)
(слайд 9-10)
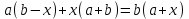
Преобразуем левую часть равенства:
а(в - х) + х(а + в) = ав – ах + ах + хв = ав + хв =
= в(а + х)
(слайд 11- 12)
П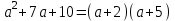 реобразование правой части тождества так, чтобы получилась её левая часть реобразование правой части тождества так, чтобы получилась её левая часть
Преобразуем правую часть равенства
(а+2)(а+5)= а² + 5а + 2а+ + 10 = а² + 7а + 10
(слайд 13-14)
Преобразование обеих частей тождества…..(должны получится одинаковые выражения)
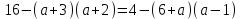
Преобразуем обе части равенства
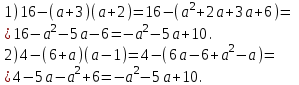
(слайд 15 – 16)
Найти разность между правой и левой частями выражения. (если эта разность равна нулю, то данное выражение - тождество)
(m-a)(m-b) = m²- (a+b)m + ab
Решение:
(m-a)(m-b) – [m² - (a+b)m + ab] =
=m² - mb – ma + ab - [m² - am – bm + ab ] =
= m² - mb – ma + ab - m² + am + bm - ab =
= 0
|
решают в тетрадях, ответ говорят с места
делают вывод
делают предположения
Равенство 3(х+у) и 3х+3у верно при любых значениях х и у. Такие равенства называются тождествами.
рассуждаем вместе и записываем
|
П: уметь добывать новые знания (находить ответы на вопросы используя учебник, свой жизненный опыт и информацию полученную на уроке)
Р: уметь работать по коллективно составленному плану, проговаривать последовательность действий на уроке
К: уметь слушать и понимать других, оформлять свои мысли в устной и письменной речи
|
6. Физкультминутка
|
Все умеем мы считать
Раз, два, три, четыре, пять —
Раз! Подняться потянуться.
Два! Согнуться, разогнуться.
Три! В ладоши три хлопка,
Головою три кивка.
На четыре - руки шире.
Пять — руками помахать.
Шесть — за парту тихо сесть.
|
Выполняют потихоньку
|
|
7. Перенос приобретенных знаний и их первичное применение в новых условиях с целью формирования умений
|
№ 334 (устно)
а) да е) нет л) да
б) да ж) да м) да
в) да з) да
г) да и) да
д) нет к) да
№ 336 (а, в, д, ж).
а) Преобразуем правую часть равенства к левой.
-(b – a) = -b + a = a – b;
в) Преобразуем левую часть равенства к правой.
(x – y)(x +y) = x2– xy + xy – y2 = x2 – y2;
д) Преобразуем левую часть равенства к правой.
(m – n)(m2 + mn +n2) = m3 + m2n + n2m – m2n– n2m – n3 = m3 – n3;
ж)Преобразуем левую часть равенства к правой.
(p + 1)(p + 1)(p + 1) = (p2 + p + p + 1)(p + 1) =
= (p2 +2p +1)(p + 1) = p3 + p2 + 2p2 + 2p + p + 1 =
= p3 + 3p2 + 3p + 1.
№ 337 (а, в, д, ж).
а) Преобразуем левую часть равенства к правой.
a(b – c) + b(c – a) + c(a – b) = ab – ac + bc – ab + ac – bc = 0;
в) Преобразуем левую часть равенства к правой.
(m – n)(2m + 3n)(m – 7) + 7(2m2 + 2mn – 3n3) =
= (2m2 + 3mn– 2mn - 3n2)(m – 7) + 7(2m2 + 2mn – 3n3) =
= (2m2 + mn - 3n2)(m – 7) + 7(2m2 + 2mn – 3n3) =
= 2m3- 14m2 + m2n – 7mn - 3mn2 + 21n3 + 14m2 + 14mn – 21n3 =
= 2m3 + m2n – 3mn2 +7mn = m(2m2 + mn – 3n2 + 7n);
д) Преобразуем левую часть равенства к правой.
(a2 – 4a + 4)(a2+ 4a + 4) – a2(a2 – 8) =
= a4 + 4a3 + 4a2 – 4a3 - 16a2– 16a + 4a2+ 16a + 16 – a4 + 8a2 = 16.
ж) )Преобразуем левую часть равенства к правой.
(a – 1)(a +1)(a2 + 1)(a4 + 1) – a8 =
= (a2 + a – a – 1)(a2 + 1)(a4 + 1) – a8 = (a2 – 1) )(a2 + 1)(a4 + 1) – a8 =
= (a4 + a2 – a2 – 1)(a4 + 1) – a8 = (a4 – 1)(a4 + 1) – a8 =
= (a8 +a4 – a4 – 1) – a8 = a8 – 1 – a8 = -1.
№ 1016 (а)
а) Пусть объем бассейна – 1.
1) 1/12 (часть) бассейна 1ая труба за 1 час
2) 1/24 (часть) бассейна 2ая труба за 1 час.
3) 1/12 + 1/24 = 3/24 = 1/8 (часть) бассейна две трубы за 1 час
4) 1 : 1/8 = 8 (часов) весь бассейн заполнят обе трубы
|
Один ученик у доски остальные в тетрадях
самостоятельно, с последующей взаимопроверкой
|
П: делают предположения об информации, которая нужна для решения учебной задачи.
К: умеют критично относиться к своему мнению
Р: понимают причины своего неуспеха и находят пути выхода из него.
|
7. Рефлексия (слайд 19)
|
|
Я все понял, урок понравился. (Что понравилось на уроке?)
На уроке было не интересно. (Почему вы так считаете?)
Я ничего не понял и с нетерпением ждал окончания урока.
С каким настроением вы уходите с урока?
Все ли цели достигли?
Как вы себя оценили бы?
|
Отвечают с места
|
Р: уметь оценивать правильность выполнения действий
|
8. Постановка Д/З
|
|
п. 5.9. № 336 (б, е, г. З), № 337 (б, г, е, з), 1016 (б), 848 (в, г) подготовиться к контрольной работе.
|
записывают.
|
|
|
|
|
 Скачать 69.76 Kb.
Скачать 69.76 Kb.
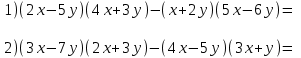
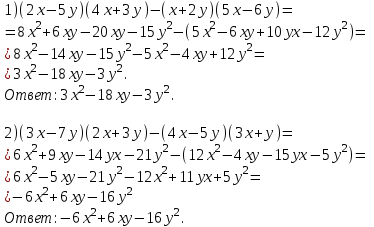
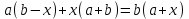
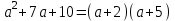 реобразование правой части тождества так, чтобы получилась её левая часть
реобразование правой части тождества так, чтобы получилась её левая часть