Курсовой ОТЦ-2. ОТЦ_Сх.38.П3.ОИ.М4. Томский университет систем управления и радиоэлектроники
 Скачать 0.78 Mb.
|
из полученных корней физическому смыслу удовлетворяют только второй и четвертый корни, т.е. в нашей цепи 2 резонанса: первый (токов) наблюдается на 1, второй (напряжений) на 1.41.Определим резонансное сопротивление цепи, т.е. подставим  в выражение  . Получим:  . Все произведенные выше вычисления оказались верными, это показал расчет резонансных частот и сопротивлений. 3.2. Исследование транзистора с обобщенной нагрузкой. 3.2.1. Вывод операторных выражений на основе МУП и проверка полученных выражений всеми возможными способами. 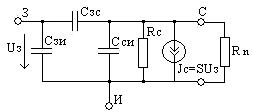 Рисунок 3.12 Схема транзистора с обобщенной нагрузкой. Представим транзистор (рис.3.12) через схему проводимостей с пробным источником. 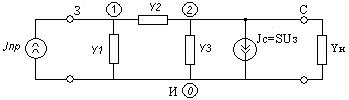 Рисунок 3.13 Схема транзистора в МУП.      Запишем ММЦ в матричной форме. 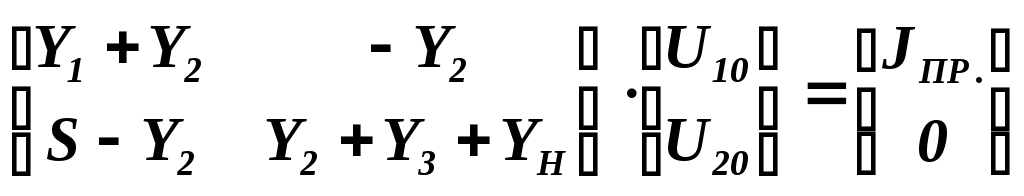 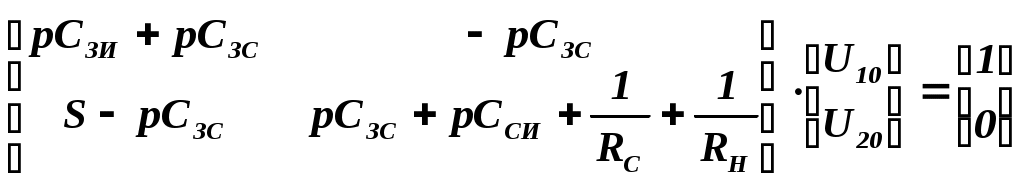 Входное сопротивление транзистора:  Проверка: 1. Размерность. 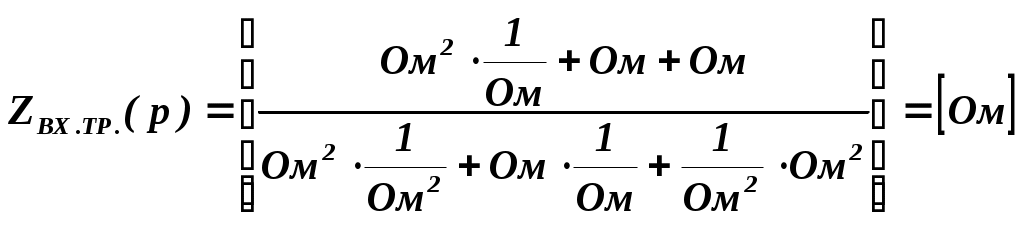 .2. Крайние частоты. 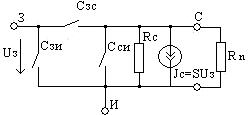 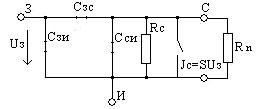    (по схеме)  (по схеме) (по выражению) (по выражению)рис.3.14 Схема транзистора на крайних частотах 3. Порядок.    При   определяется емкостным сопротивлением т.к.  , значит сопротивление закорачивается   < При  определяется емкостным сопротивлением т.к.  , значит минимальная степень числителя меньше на единицу степени знаменателя.Передаточная функция:  Проверка: 1. Размерность. 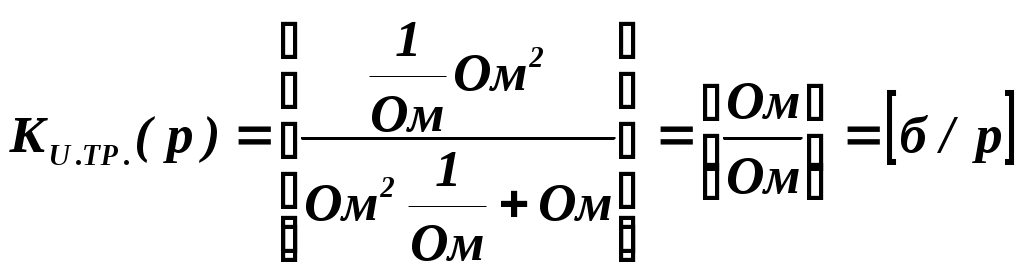 2. Крайние частоты. Проверку на нулевой частоте для транзистора проводят сравнивая полученное выражение на  с качественным выражением, которое выполняется на области частот, где S практически не зависит от частоты. Для полевого транзистора с ОИ оно выглядит так:  Видно, что на у нас  совпадает. Знак минус соответствует об инверсии фазы. На бесконечно большой частоте известно, что  , следовательно, значение не зависит от зависимого источника, в этом случае он определяется емкостным делителем  и  .А судя по полученному выражению это условие полностью выполняется: 3.2.2. Нормировка операторных функций. •Ненормированные значения.  пФ  мА/В пФ  Ом пФ• Нормирующие значения.   • Нормировка.       Таблица 3.6
 • Нормированные функции. Входная функция: 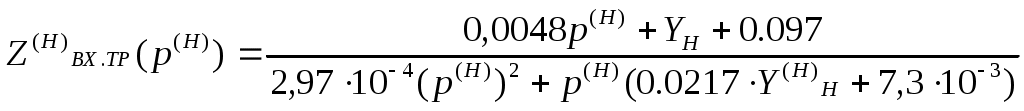  Передаточная функция:   3.3. Исследование транзистора с избирательной нагрузкой. 3.3.1. Предполагаемый характер ЧХ 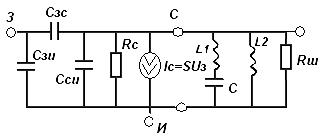 Рисунок 3.15 модель полевого транзистора с избирательной нагрузкой Входная функция Слабое влияние нагрузки позволяет сделать грубую оценку ЧХ для входного сопротивления, которое в основном определяется транзистором. Значит, приблизительный характер ЧХ будет совпадать с транзисторной на крайних частотах. На рисунке 3.29. представлена АЧХ входной функции. 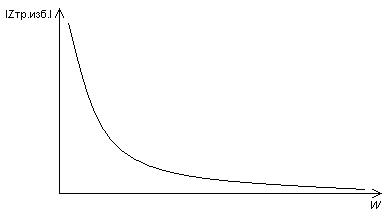 рис.3.16 АЧХ входной функции   Учитывая слабое влияние нагрузки на входное сопротивление и то, что на крайних частотах ФЧХ определяется емкостью, получим приблизительный характер ФЧХ входной функции: 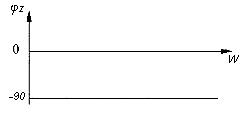 рис.3.17 ФЧХ входной функции Передаточная функция Чтобы предположить какой характер ЧХ имеет передаточная функция приведем следующее соотношение:  из него следует, что АЧХ:  ФЧХ:  , где 180 – соответствует инверсии фазы  - в рабочем диапазоне имеет нулевое значение, при очень высоких частотах  .Приведенные выше выражения не являются точными и пригодными для оценки качественного анализа ЧХ. В соответствии с выше приведенным выражением АЧХ ожидаемый результирующий график будет иметь вид:  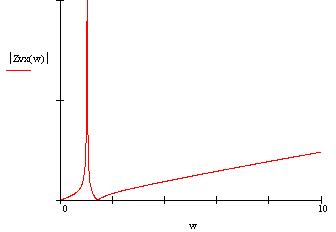 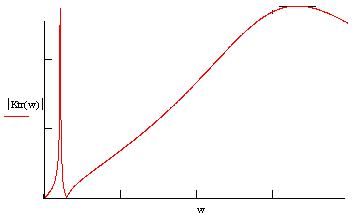 Рисунок 3.18 предполагаемое АЧХ передаточной функции Определим ФЧХ передаточной функции на .Φк(0)=-180+ ΦZн+ ΦКн=-180+0+0= -180 3.3.2.Получение выражений входной и передаточной функций и их проверка всеми возможными способами. Входная функция Получение нормированного выражения входной функции осуществляется при помощи подстановки во входную функцию транзистора проводимости избирательной нагрузки. Входное сопротивление транзистора с обобщенной нагрузкой: 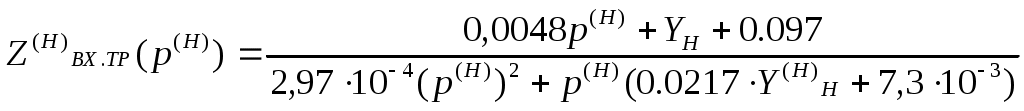После подстановки нормированного выражения проводимости нагрузки, получим:  Учтем, что  , т.о. нормированное выражение для входной функции избирательной нагрузки с транзистором примет вид: Z0=49,49 проверка : 1).проверка на крайних частотах:   2) Порядок.  При  определяется емкостным сопротивлением т.к. , значит сопротивление закорачивается < При определяется емкостным сопротивлением т.к. , значит минимальная степень числителя меньше на единицу степени знаменателя.Передаточная функция Для передаточной функции проводятся те же операции, что и для входной. Передаточная функция для транзистора с обобщенной нагрузкой: Передаточная функция для транзистора с избирательной нагрузкой:  К0=0.3 3.3.3 Предполагаемый характер ЧХ на основе на основе карты нулей и полюсов и вычисление значений ЧХ на  =1.5.• Входная функция Z0=49,49 нули: полюса: 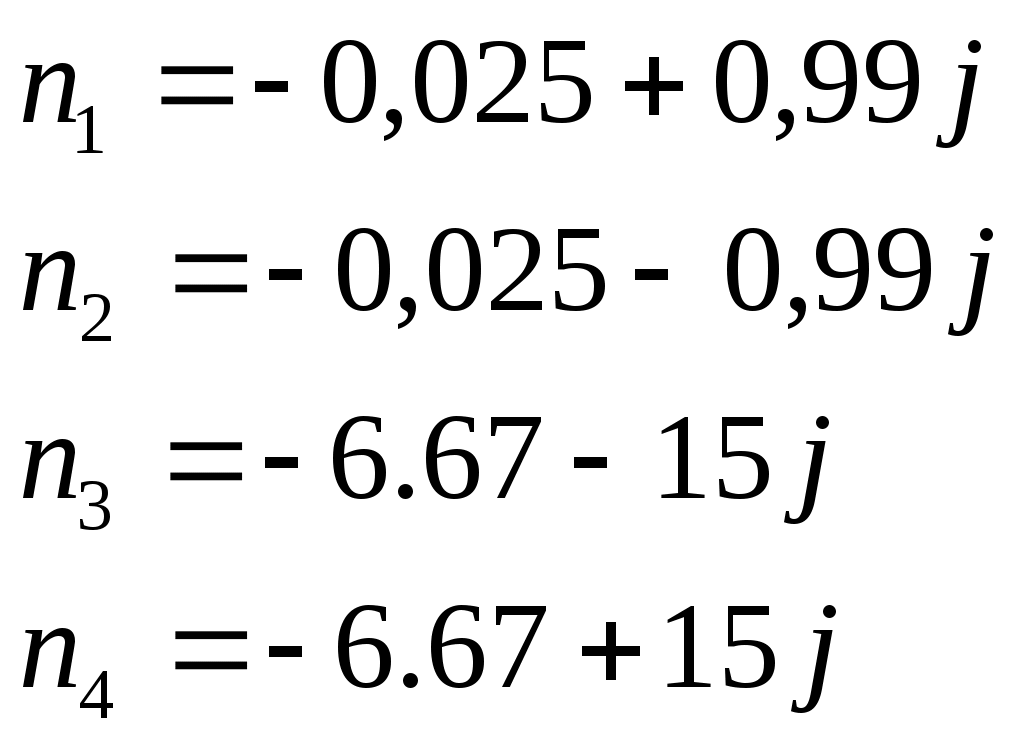 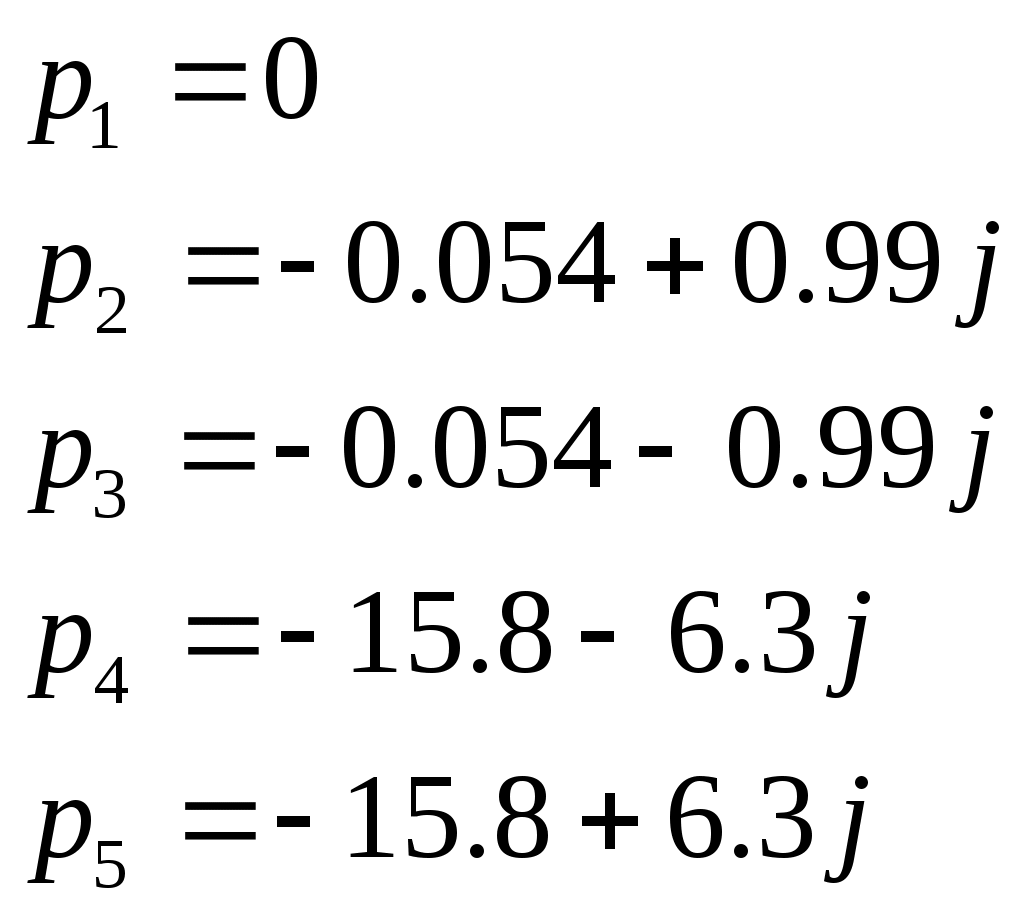 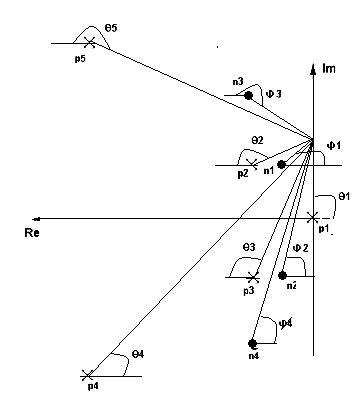 Рисунок 3.19 ПНИ входной функции Ниже в таблицах 3.7 и 3.8 приведены значения длин векторов и углов для заданной нормированной частоты ωн=1.5. Таблица 3.7 Длины векторов входной функции
Таблица 3.8 Углы. Входной функции
АЧХ:  ФЧX:  На  :АЧХ:  ФЧХ: Посмотрим, как себя ведет АЧХ и ФЧХ входной функции на крайних частотах. Имеем:  :  АЧХ:  АЧХ:  ФЧХ:  ФЧХ: Построим в MathCad АЧХ и ФЧХ нормированной входной функции транзистора с избирательной нагрузкой и произведем сравнение с предположительным характером ЧХ и тем, что мы получили, воспользовавшись ПНИ. На рисунке 3.20 приведен модуль , а на рисунке 3.21 фаза входного сопротивления транзистора 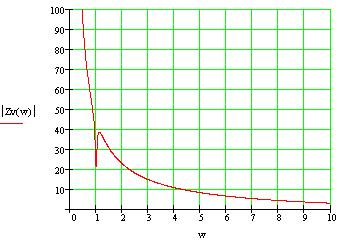 .Рисунок 3.20 Модуль входной функции. 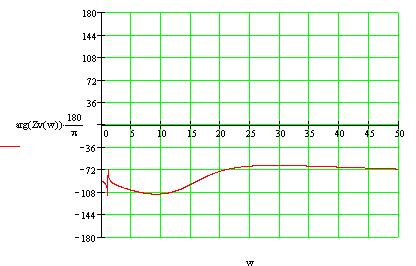 Рисунок 3.21 Аргумент входной функции. Из графиков видно, что наши вычисления по карте нулей и полюсов оказались верными на крайних частотах и заданной частоте. Потому как у нас все нули и полюса находятся в левой полуплоскости один полюс в нуле, цепь является устойчивой. |
, пФ
,пФ
,Ом
,мА/В